基于气动参数辨识的弹道风速估计算法设计
2014-07-08张衍儒肖练刚张继生
张衍儒 肖练刚 张继生 田 丰 陈 昌
北京航天自动控制研究所,北京 100854
基于气动参数辨识的弹道风速估计算法设计
张衍儒 肖练刚 张继生 田 丰 陈 昌
北京航天自动控制研究所,北京 100854

首先介绍低空风分布,确定风速估算范围。然后,以射程预测为主要研究目标,通过弹上传感器信息分析飞行过程中的实时气动阻力,对比在无风条件下的气动阻力理论值,采用气动参数辨识算法实时估算纵向风的近似风速,从而提高射程预测的精度。估算过程中,采用最小二乘算法计算不同风速下的气动阻力系数常值项,利用迭代算法求取气动阻力系数常值项为理论值时所对应的设定纵向风,即实际纵向风的近似值。最后通过仿真试验给出了估算算法的分析结果,该算法可以实时估算风速用于射程预测,并具有运算速度快,计算负荷小等优点,适合于工程实际应用。
制导弹药;气动参数辨识;最小二乘算法;风速估计
目前,部分制导弹药采用预测落点的方式进行制导控制,如美国XM1156式制导炮弹[1]、RCGM式制导迫击炮弹[2]等。预测落点过程中,需要分析弹道风速,如美国XM1156式制导炮弹利用发射前半小时的气象分析数据,进行落点预测。90年代,Mark F.Costello对有风条件下,鸭舵式制导迫击炮弹道仿真模型进行了详细的研究[3],从而在风速已知的条件下提高了预测落点的精度。2008年,赵庆岚[4]对有风条件下末制导炮弹弹道模型进行了研究,同样提高了预测落点的精度。但是,上述方法需要在射前进行风速测定,并且重新生成射表,用于射前数据装订。2011年Frank Fresconi等人[5]对弹上实时落点预测算法进行了理论研究,利用弹上GPS提供的位置、速度信息积分求取预测落点。该方法由于利用弹上实时数据进行落点预测,落点精度有显著提高,但是需要进行大量的积分运算,计算负荷大,对于全程实时控制的制导弹药,此种方式并不适用。为保证预测的实时性,可以采用Jonathan Rogers等人[7]提供的完整的无风仿真模型,利用在标准气象条件下的气动参考值,建立基于导航系下弹体三维速度、三维位置的落点预测插值表。落点预测插值表在发射前装订到弹丸中,弹丸在飞行过程中实时查询预测表,采用插值方式进行落点预测。此方式可以大幅降低处理器计算负荷,但由于未考虑风速影响,降低了预测精度。
本文在未知风速的条件下,利用弹上加速度计、GPS和弹体姿态角信息实时分析飞行过程中的气动阻力,对比在无风条件下的气动阻力理论值,采用气动参数辨识算法[8-9]实时估算纵向风的近似值,并利用纵向风对射程的修正模型,完成对射程预测值的修正,从而提高射程预测的精度。
1 风的分布和纵向风对射程的修正
习惯上将风力大小用风力等级来描述[10],如0~10级风分别称为无风、软风、轻风、微风、和风、清劲风、强风、疾风、大风、烈风、狂风。风力等级K与平均风速W可用下式换算:
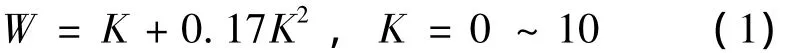
由式(1)可知,低空风速大小范围在26.4±2m/s以内。因此文中考虑的风速设定值范围为-40 ~40m/s。
可以根据目前弹体速度v0、射角θ0和高度H,采用插值的方式进行弹道的射程预测。在有纵风wx时,可由式(2)求取动坐标系中相对速度vr与相对射角θr:
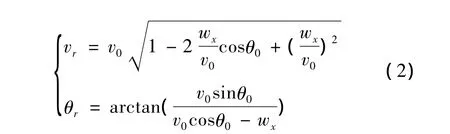
根据所求相对速度vr、相对射角θr和高度H,采用插值的方式求取相对射程Xr与飞行时间T,由式(3)求取修正后预测射程Xwx:

由式(3)可以看出,修正模型的纵风wx是指弹道的平均风速,因此估算纵风风速时,应滤掉短时随机风,保证射程修正模型的有效性。
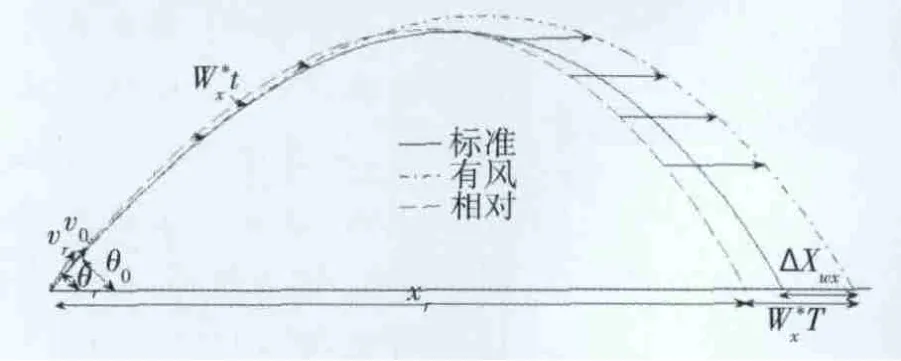
图1 纵风对射程的修正曲线
图1介绍了修正过程包含的3条曲线:“标准”曲线表示未修正时的预测弹道;“相对”曲线表示在动坐标系中求取的相对弹道;“有风”曲线表示修正后的预测弹道。图中预测弹道参数包含弹体速度v0,射角θ0和高度H,相对弹道参数包含相对速度vr,相对射角θr和高度H,修正后的预测弹道参数包含相对射程Xr,飞行时间T和纵风wx。
2 气动参数辨识算法
制导弹药气动阻力的三维分量可用式(4)表示:
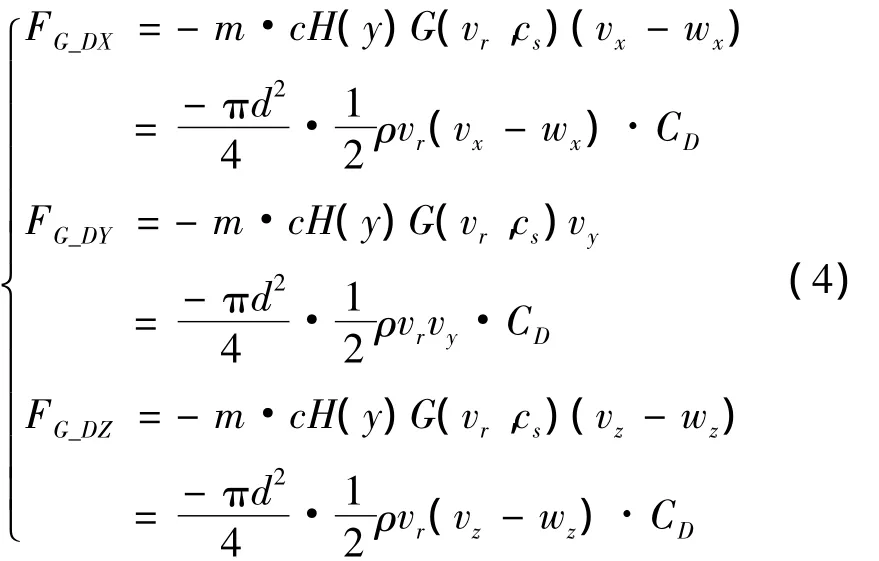
式中:FG_DX,FG_DY,FG_DZ是制导弹药气动阻力的三维分量,m,c,H,y,G,vr,cs是弹体质量、弹形系数、空气密度函数、高度、阻力函数、相对速度、声速;vx,vy,vz是导航系下弹药速度;wx,wz是导航系下纵向风速度、横向风速度;d,ρ是弹体特征长度、空气密度;CD是气动阻力系数。
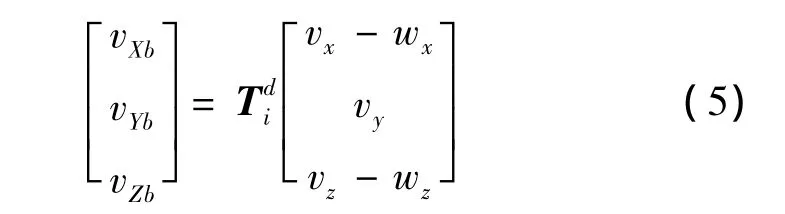
通过式(6),求取攻角α、侧滑角β、弹体速度与弹体轴向之间的夹角αT:
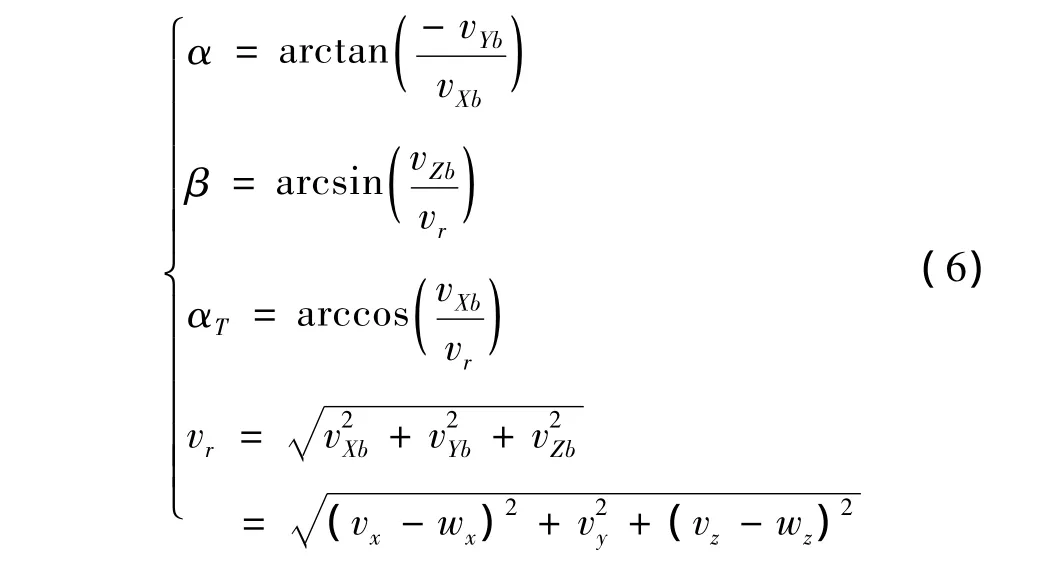
利用加速度计测量值aximu,ayimu,azimu和弹体姿态信息α,β,通过式(7)可以实时计算与弹丸速度反向的制导弹药气动阻力FACC_D。
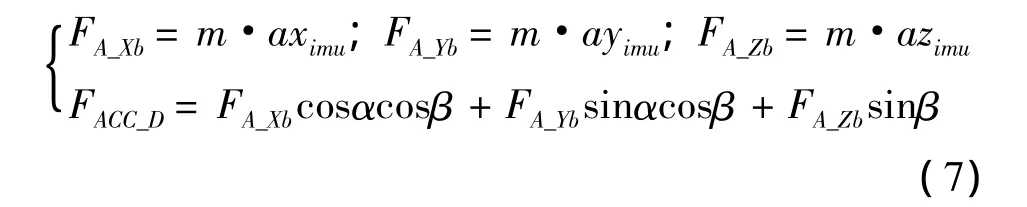
式中,FA_Xb,FA_Yb,FA_Zb表示加速度计测得的弹体三维气动力;FACC_D表示通过加速度计计算得到的制导弹药气动阻力。
通过式(6)和(7),可以得到气动阻力FACC_D关于弹体速度vXb,vYb,vZb和加速度aximu,ayimu,azimu的表达式:
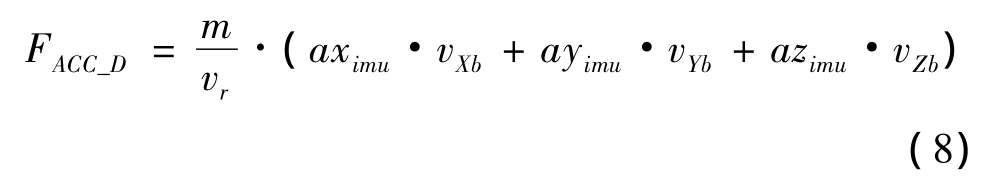
计算得到的气动阻力FACC_D与气动阻力三维分量FG_DX,FG_DY,FG_DZ存在关系式(9):
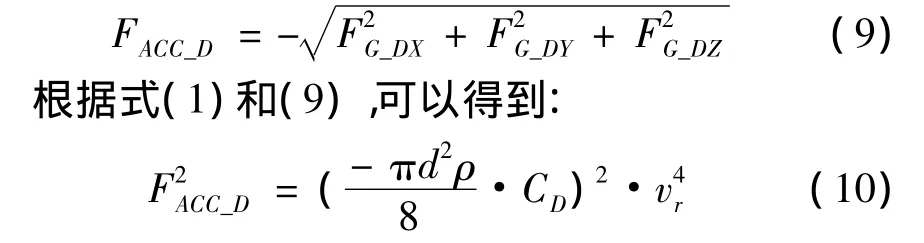
根据式(8)和(10)可以得到式(11),用于计算气动阻力系数CD:
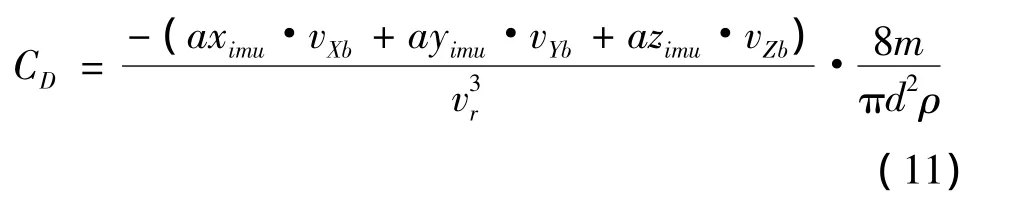
气动阻力系数CD,主要受到弹体马赫数、弹体轴向与弹体速度之间夹角αT、气温、气压、空气湿度、舵角等项的影响。其中αT的变化对CD数值变化影响较大,因此用式(12)近似αT对CD的影响:
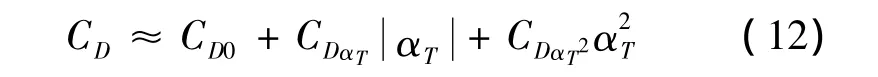
式中,CD0为气动阻力系数常值项,CDαT,CDαT2表示气动阻力系数关于αT的1,2阶变化量。
利用计算得到的气动阻力系数CD求取气动阻力系数的常值项CD0,求取过程如下:
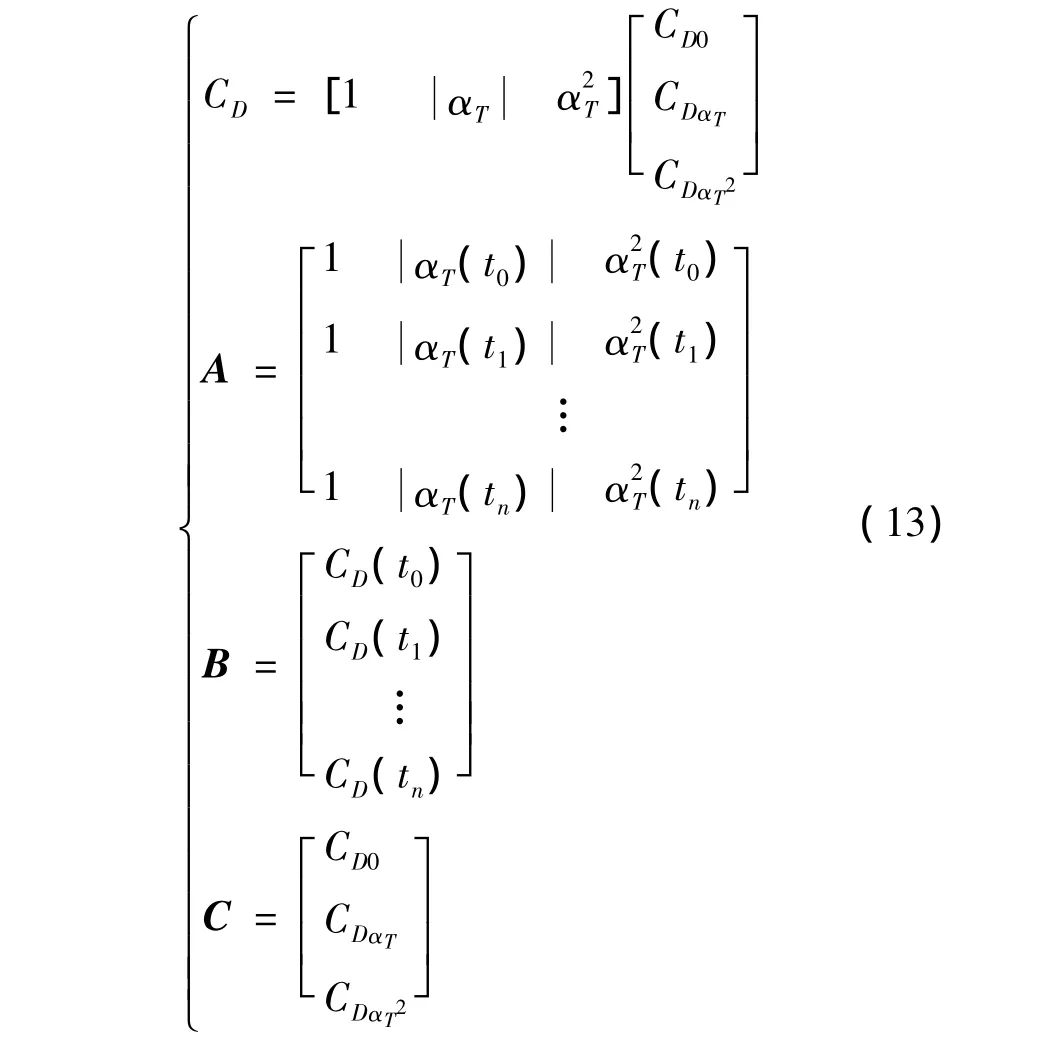
应用最小二乘估计法,得到C的估计值为
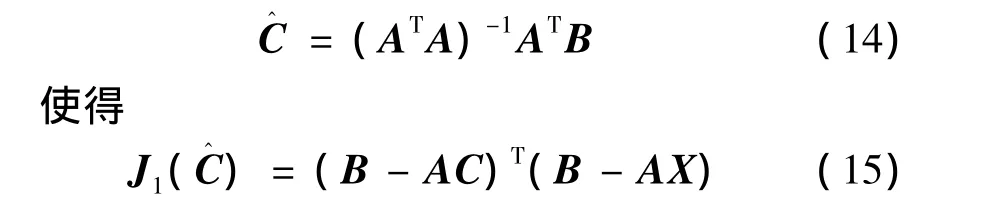
取极小值。
由求取的C的第一行值可以确定气动阻力系数常值项CD0。
3 风速迭代算法
对于全程控制的制导弹药,横向控制可以全程采用比例导引进行精确制导,因此横向风的影响可以通过舵控进行实时修正。但是制导弹药在上升段飞行时纵向控制算法需要实时预测射程用于精确制导控制,考虑到纵向风对预测射程的影响,本文设计了风速迭代算法实时求取纵向风的近似值,用于预测射程的修正。
通过第2节对气动参数辨识算法的介绍,可知气动阻力相同时,设定不同风速w'x(k)会对应不同的气动阻力系数常值项C'D0(k),由于气动阻力系数常值项CD0仅受到弹体马赫数、气温、气压、空气湿度和舵角等项的影响,因此可以通过装订在弹上由风洞试验提供的相关插值表,快速计算其实际的参考值CDref,只有当C'D0(k0)≈CDref时,设定的w'x(k0)才是实际纵向风的近似值。下面详细介绍一下迭代算法的工作原理:
1)根据风的分布,本文设定纵向风速的迭代范围为-40~40m/s,由于横向控制算法修正了横向风的影响,因此设定纵风与横风为:
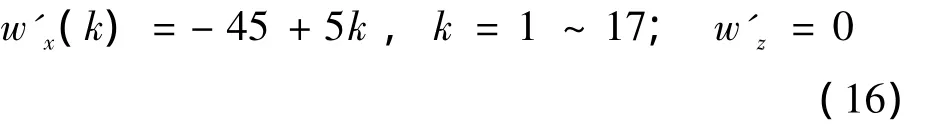
利用导航初始化过程中的前10组共1s的数据,通过设定不同风速w'x(k)采用气动参数辨识算法,求取不同设定风速所对应的气动阻力系数常值项C'D0(k),k=1~17。
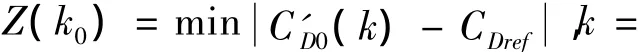
2)初步确定风速w'x(k0)后,缩小纵风设定范围进行精确求取,设定风速为:
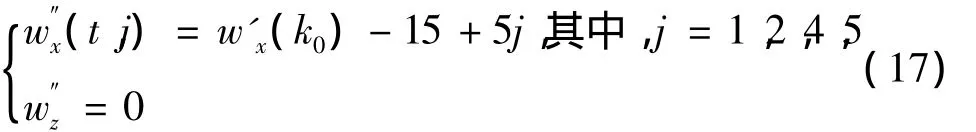
式中,t为采样次数,单位为s。
每隔1s时间,求取一次设定风速(t,j)所对应气动阻力系数常值项(t,j)和实际参考值CDref(t)之间的差值绝对值。在介绍纵向风对射程的修正模型时,已经说明修正模型中所采用的纵风wx是指弹道的平均风速,因此估算纵风风速时,应滤掉短时随机风,保证射程修正模型的有效性。为消除零均值噪声和短时随机风的影响,采用求和的方式记录差值绝对值的累加值
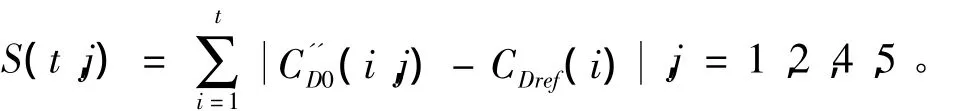
3)根据求取的S(t,j)(j=1,2,4,5)变化和初步确定的风速w'x(k0),利用式(20)实时求解采样时刻为t时,纵向风的近似值wx(t):

根据式(18)所得纵风的近似值wx(t),可以采用式(2)与(3)进行预测射程的实时修正。
4 仿真试验与误差分析
通过软件流程图再次介绍利用迭代算法求取纵风近似值的过程,如图2。
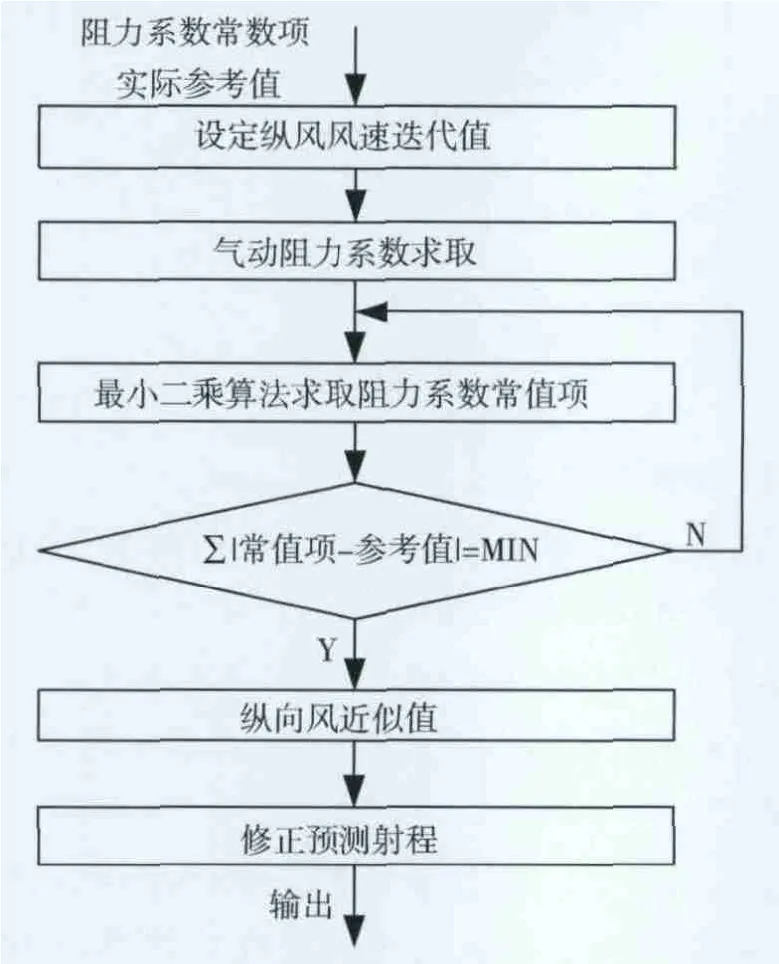
图2 风速估计算法软件流程图
在仿真试验中,设定实际纵向风速wx=20,设定不同的风速w'x(k)=0,10,20,40 ,通过最小二乘算法计算不同设定风速所对应的气动阻力系数常值项C'D0(k),如图3所示。
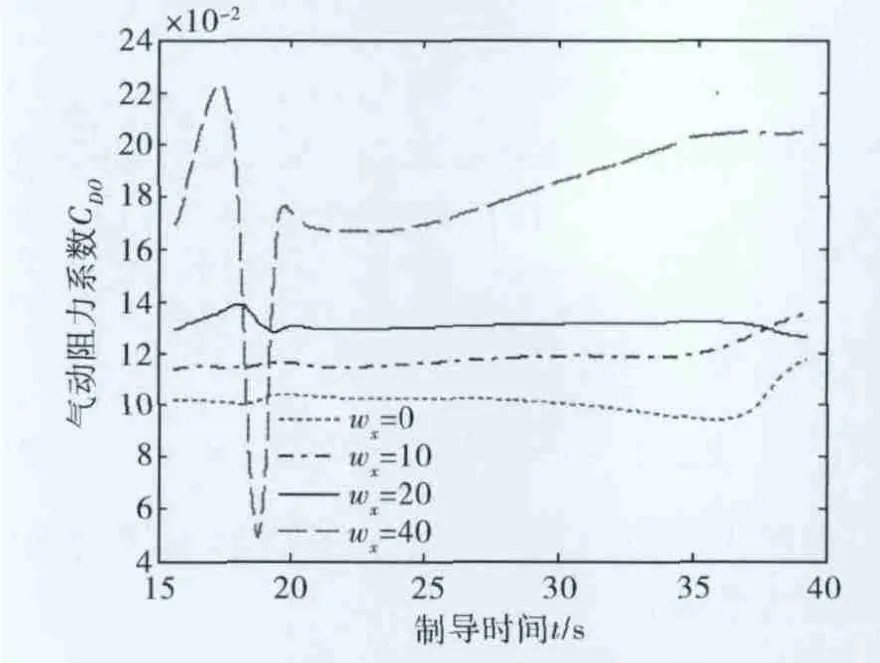
图3 最小二乘算法求取气动阻力常值项
根据图3可知,不同设定风速w'x(k)代入会对应不同的气动阻力系数常值项C'D0(k)。当设定风速w'x(k)越接近实际风速wx时,C'D0(k)与由风洞试验提供的实际参考值CDref之间差值绝对值的累加项S(t)越小,如图4所示。
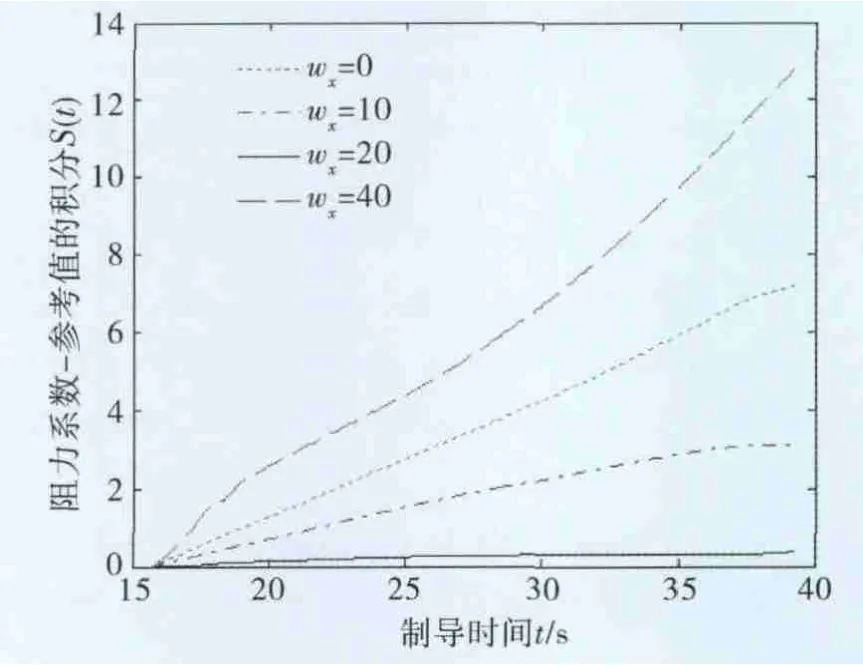
图4 不同风速设定的S(t)值变化
图4显示了不同风速设定对应的S(t)值变化,可以看出设定风速越接近于实际风速,S(t)值越小。
采用风速估算算法,进行4组仿真试验,设定实际纵向风速wx=-14,0,14,20 ,求取近似风速,求取过程中的迭代曲线如图5所示。
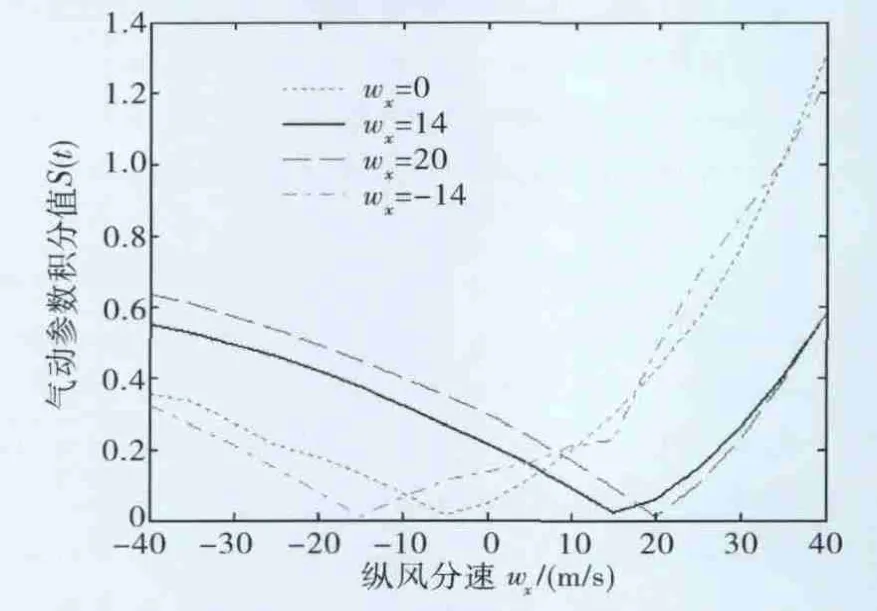
图5 利用迭代算法求取不同实际风速曲线
图5中,X向表示纵向设定风速,Y向表示差值绝对值的累加项S(t)的变化,可以看出设定风速从实际风速的两侧逐渐收敛,最后收敛到最低累加值,此位置的设定风速近似为实际风速,从而证明了风速估算算法的快速性与准确性。近似风速与实际设定风速之间存在一定误差,误差来源于舵角与横向风的变化对风速求取过程的影响。
采用仿真试验,对比采用风速估算算法修正前后的预测射程与实际射程之间偏差变化曲线,如图6所示。图中X向表示制导弹药飞行时间,Y向表示预测射程与实际射程之间的偏差,通过对比可以看出采用修正算法后,飞行控制时间大幅降低,在20s时,修正过程就已经完成,而未采用修正算法,由于预测射程的误差需要长时间的比例导引进行制导修正,这对弹体结构、强度要求、舵机功率要求、弹上仪器设备和减少制导误差都是不利的。
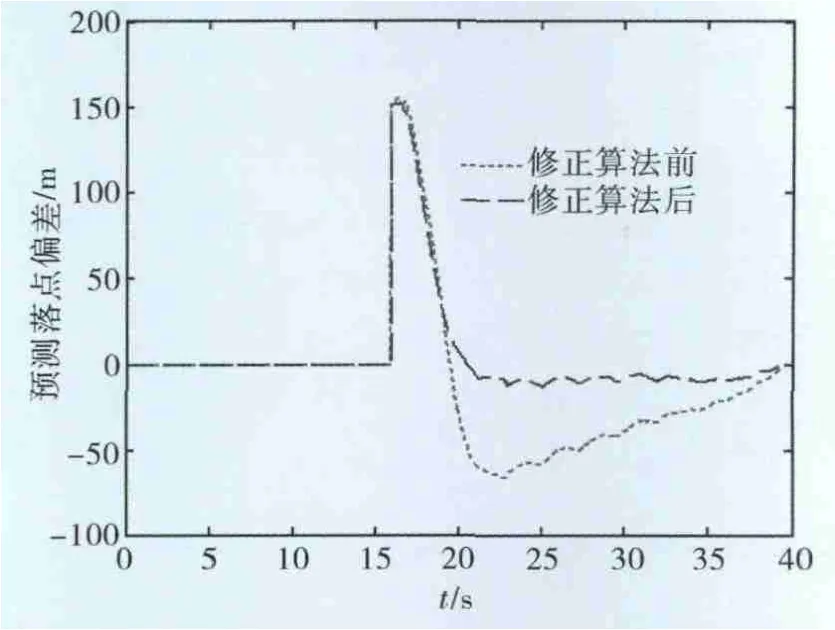
图6 修正前后预测射程与实际射程之间偏差对比图
5 结论
在算法实际使用过程中气温、气压、空气湿度、舵角、横风风速等参数变化都会对算法产生影响,因此求取的风速仅仅为纵向风的近似值。虽然采用近似风速应用在射程修正时存在一定的预测偏差,但是相对于不考虑风速的预测方式却大幅提高了预测精度,同时相对于积分方式的预测算法,也降低了处理器计算负荷,增强了算法的实时性与可应用性,为制导弹药提高预测射程精度提供了可行性方案。
[1]Peter Burke.XM1156 Precision Guidance Kit(PGK)Overview[C].NDIA-53rd Annual Fuze Conference,2009.
[2]Yousef Habash.Roll Control Guided Mortar(RCGM)[C].America:NDIA Joint Armaments Conference,2012.
[3]Mark F.Costello.Range Extension and Accuracy Improvement of an Advanced Projectile Using Canard Control[C].AIAA Atmospheric Flight Mechanics Conference in Baltimore,Maryland,1995:324-331.
[4]赵庆岚,宋卫东,鲁飞,乔梁.有风条件下末制导炮弹弹道模型研究[J].工程设计学报,2008,5(15):373-376.(Zhao fenglan,Song Weidong,Lu Fei,Qiao Liang.Research on Terminal-guidance Ballistic Model under Windy Condition[J].Journal of Engineering Design,2008,5(15):373-376.)
[5]Frank Fresconi,Gene Cooper,Mark Costello.Practical Assessment of Real-Time Impact Point Estimators for Smart Weapons[J].Journal of Aerospace Engineering,2011,1(24):1-11.
[6]王敏忠.炮兵应用外弹道学及仿真[M].北京:国防工业出版社,2009:25-28.(Wang Minzhong.Artillery Applied Exterior Ballistics and Simulation[M].Beijing:National Defence Industry Press,2009:25-28)
[7]Jonathan Rogers,Mark Costello.Design of a Roll-Stabilized Mortar Projectile with Reciprocating Canards[J].Journal of Guidance,Control,and Dynamics,2010,4(33):1026-1034.
[8]戴明祥,杨新民,易文俊,何颖.用于卫星制导弹药落点预测的卡尔曼滤波算法[J].弹箭与制导学报,2012,5(32):117-120.(Dai Mingxiang,Yang Xinmin,Yi Wenjun,He Ying.Kalman Filtering Algorithm for Impact Point Prediction of Satellite Guided Projectile[J].Jouranl of Projectiles,Rockets,Missile and Guidance,2012,5(32):117-120.)
[9]Luisa D Fairfax and Frank E Fresconi.Position Estimation for Projectiles Using Low-cost Sensors and Flight Dynamics[R].America:Army Research Laboratory,2012.
[10]韩子鹏,等.弹箭外弹道学[M].北京:北京理工大学出版社,2008:14,96-98.(Hang Zipeng,et al.Exterior Ballistics of Rockets and Missile[M].Beijing:Beijing Institute of Technology Press,2008:14,96-98.)
[11]George M Siouris.Missle Guidance and Control Systems[M].Beijing:National Defence Industry Press,2010:43.
Estimation of Ballistic Wind Speed Base on Aerodynamic Parameter Identification
ZHANG Yanru XIAO Liangang ZHANG Jisheng TIAN Feng CHEN Chang
Beijing Aerospace Automatic Control Institute,Beijing 100854,China
In the predictive process,guided munitions needed analysis of ballistic wind speed to improve the impact point precision.This paper introduced the wind distribution to determine wind speed estimation range.Then,according to the wind tunnel experimental data,the aerodynamic reference value of standard model and ballistic aerodynamic drag model was used for aerodynamic parameter identification by using the least square algorithm.This paper used the iterative algorithm to compute the approximate value of longitudinal wind,and built range correction model.According to the simulation test results,this algorithm could be used in real time correction,it was also suitable for engineering application and had the advantages of fast computing speed and small computation load.
Guided munitions;Aerodynamic parameter identification;Least square algorithm;Wind estimation
TJ412.+1
A
1006-3242(2014)02-0029-06
2013-03-12
张衍儒(1985-),男,哈尔滨人,博士研究生,主要研究方向为制导弹药控制系统综合;肖练刚(1973-),男,四川资中人,博士,研究员,主要研究方向为导航、制导与控制;张继生(1980-),男,河北人,工程师,主要研究方向为控制系统综合;田 丰(1985-),男,江苏人,工程师,主要研究方向控制系统综合;陈 昌(1983-),男,河北人,工程师,主要研究方向为控制系统综合。
