基于滑动矩形窗和准三对角线结构的QC-LDPC码

汪汉新，王芳，苏开友，朱翠涛

中南民族大学电信学院，武汉 430074

◎信号处理◎

基于滑动矩形窗和准三对角线结构的QC-LDPC码

汪汉新，王芳，苏开友，朱翠涛

中南民族大学电信学院，武汉 430074

针对IEEE 802.16e标准QC-LDPC码的码长和码率有限，及其采用的准双对角线结构包含大量度为2的变量节点导致较高错误平层的缺陷，提出一种基于滑动矩形窗和准三对角线结构的QC-LDPC码的快速编码算法，可以灵活地扩展码长和码率的范围，改善纠错性能，降低编码复杂度，适合于变速率的自适应传输系统。

准循环低密度奇偶校验（QC-LDPC）码；对角线结构；度分布；编码复杂度

1 引言

QC-LDPC码结构简单，易于高效编码，适合硬件实现，因此在通信领域得到广泛的应用，如移动宽带无线接入标准IEEE 802.16e QC-LDPC码[1-5]。然而标准QC-LDPC码中的码率和码长数量有限，在IEEE 802.16e中只有1/2，2/3，3/4和5/6总共4种码率，码长也只有19种，最小为576，最大为2 304，步长为96，严重制约了LDPC码的实际应用范围，不能满足自适应传输系统中码长和码率灵活变化的要求。另外，标准QC-LDPC码通常采用准双对角线的下三角结构，编码效率和误码性能不太高。虽然通过最大化ACE和最小误码率准则等算法对QC-LDPC码的循环移位次数和度分布进行优化可以提高纠错性能，但是算法的复杂度较高，且无法连续对一系列不同码长进行优化[6-8]。另外，为实现快速编码，学者们也相继提出了几种准双对角线的改进结构，如三对角线结构、新下三角结构和后向迭代结构。然而三对角线结构要求严格，不能灵活变化，新下三角结构和后向迭代结构包含大量度为2的变量节点，会导致较高的错误平台，并且这些改进结构的QC-LDPC码大多码长和码率受限，达不到灵活变化的要求[9-13]。本文提出一种基于滑动矩形窗和准三对角线结构的QC-LDPC码的构造方法，通过滑动矩形窗实现码长和码率的灵活变化，采用去对角线法实现优化度分布，并通过调整准三对角线结构的第三条对角线的位置来消除部分度为2的变量节点，达到降低错误平层的目的。

2 滑动矩形窗结构

2.1 H b1矩阵的滑动矩形窗构造法

LDPC码由一组循环移位矩阵构成，其校验矩阵H的置换子矩阵的下标Sij构成的矩阵Hs的结构如式（1）：

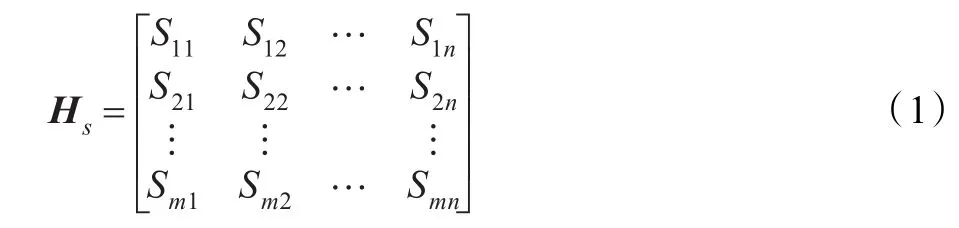
其中，Sij(1≤i≤m，1≤j≤n)∈(-1，0，N)表示矩阵中第i行第j列置换矩阵的循环移位次数，-1表示零矩阵，0表示单位矩阵，正整数N表示单位矩阵的循环右移位矩阵；若扩展因子z表示置换矩阵的维数，则Hs扩展后的H矩阵大小为mz×nz。

在QC-LDPC码的H矩阵的构造中，最重要的是避免4环的存在，若循环移位次数Sij满足式（2），且z满足一定值时，则构造的矩阵无4环。

基于准双对角线结构的QC-LDPC码的基本校验矩阵Hb可表示为式（3）～式（5）。

其中，Hb1和Hb2分别为Hb矩阵中的信息比特部分和校验比特部分；Hb1是无4环的稀疏矩阵，大小为mb×kb；Hb2是一个固定的双对角线结构的近似下三角矩阵，大小为mb×mb，矩阵中的0和-1分别表示单位矩阵和零矩阵，b(1)=b(m)=bm（bm为小于z的素数），b(r)=0。

根据式（2），由Hs矩阵可根据式（6）构造无4环的Hb1，对应的z值应满足式（7）。其中，1≤i≤m；hf为矩阵的第一行第一列元素的值；ct为第一行公差；rt为第一列公差；m和k分别为Hb1矩阵的行值和列值。

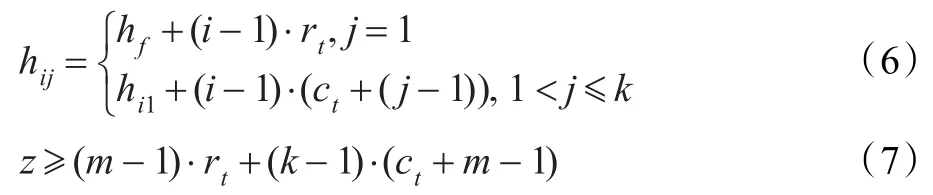
由于码率R=k/(k+m)，因此只需改变m和k的值即可实现码率和码长的改变。例如当m=k=6时，则码率R=1/2，最小码长可达6×62=372，步长为12；若要得到R=1/3码率，则在m不变的情况下，只需将k值变为3，在Hb1矩阵中相当于删除其中3列，相应的最小码长为9×16=144，步长变为9；或者将m和k的值变为4和2，则相当于删除其中2行和4列，最小码长变为6×7= 42，步长为6。可以看出，无需重新构造，只需删除一定数量的行和列即可实现码率和码长的灵活变换灵活。同时通过修改hf、ct和rt的值，能构造出不同z值和Hb1矩阵，其最终达到的效果也不尽相同，这三个值的选取可在误码率和迭代次数之间权衡。例如，当hf=1、ct=0、rt=1时，构造得到6×6的矩阵如图1中实线矩形窗覆盖的矩阵。而当hf=3、ct=1、rt=2时，得到如图1中虚线矩形窗矩阵。矩阵的变化在图1中相当于实线矩形窗向右和向下各移一位到虚线矩形窗的位置，类似于矩形窗在Hs矩阵中滑动，因此称为滑动矩形窗构造法。

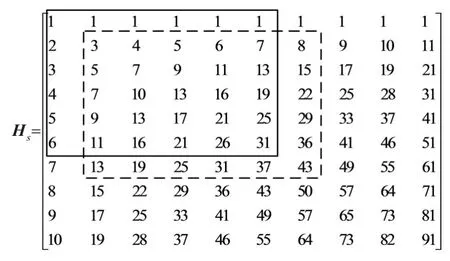
图1 矩阵H s与滑动矩形窗

滑动矩形窗构造Hb1矩阵的具体步骤如下：

（1）根据式（6）设计一个大小为m×k的矩形窗矩阵。

（2）根据扩展因子z，确定矩形窗在Hs中平移的位置。

（3）将滑动矩形窗覆盖的元素作为Hb1矩阵，与m×m的固定结构矩阵Hb2合并得到矩阵Hb。

采用滑动矩形窗构造法，在构造Hb1矩阵时，要求的z值更小，可以实现码长和码率灵活变化的QC-LDPC码，非常适合于变速率的自适应传输系统。

2.2 H b1矩阵的对角线优化方法

在滑动矩形窗构造方法中，若直接采用覆盖的矩阵作为Hb1，则构造出的QC-LDPC码中的行和列的度数相同，相当于规则LDPC码，误码率性能较差。因此本文通过去对角线优化法，将矩阵修改成具有不同度数的矩阵，能进一步提高LDPC码的纠错性能。具体方法是，将滑动矩形窗构造方法得到的Hb1矩阵中若干对角线元素用-1代替，即将这些位置的置换矩阵用零矩阵代替，实现度数分布的优化。例如将图1实线矩形框中的元素进行修改，得到如式（8）的H˜b1矩阵，经过和Hb2矩阵合并得到如式（9）的Hb矩阵。

通过滑动矩形窗构造Hb1矩阵及其对角线优化法，在实现码长和码率的灵活变化的同时，还可以提高QC-LDPC码的误码率性能。

3 准三对角线结构

3.1 H b2矩阵的准三对角线构造法

QC-LDPC码大多采用准双对角线的近似下三角结构，为了进一步提高编码效率和误码率性能，需要对准双对角线结构的Hb2矩阵进行优化。现有文献中对Hb2的优化主要有三对角线结构、新下三角结构和反向迭代结构。在三对角线结构中，有三条对角线元素不为-1，其中一条元素为0，另外两条为自然数，这两条对角线元素的值需要满足一定的条件，因此码长和码率受到限制；在新下三角结构中，除第一列有三个元素不为-1外，其余列中有两个元素不为-1；在反向迭代结构中，两条对角线位置元素为0，其余位置为-1；并且在新下三角结构和反向迭代结构中，度数为2的变量节点占了绝大部分，会导致较高的错误平层。针对这些结构的缺点，本文提出一种准三对角线结构的H˜b2矩阵的构造方法，如式（10）。其中，r(i)∈0，r(1)和r(l)分别表示第三条对角线的起始和终止位置，H˜b2矩阵的元素只有0和-1，且只有三条对角线上的元素为0；要满足无4环的条件，r(1)的行值应不小于3。

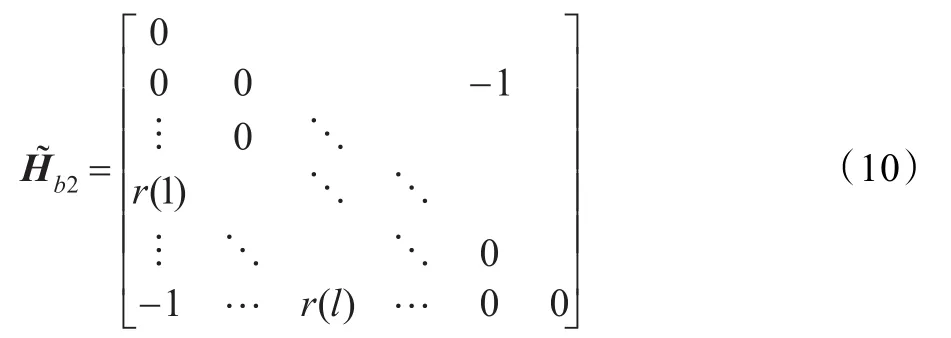
从式（10）可以看出，与三对角线结构相比，准三对角线结构具有灵活调整第三条对角线位置的优点，并且随着H˜b2矩阵维数的增加，第三条对角线可供选择的位置也随之增加；与新下三角结构和后向迭代结构相比，准三对角线结构能够消除一部分度为2的变量节点。由于第三条对角线位置选择的不同，其度分布也不同，因此可以通过合适地选择第三条对角线位置来优化QC-LDPC码的度分布，从而提高误码率性能。

根据滑动矩形窗构造法，取m=9、k=9构造Hb1，并采用准三对角线构造法构造Hb2，合并后得到Hb矩阵如图2。其中，斜线表示的第三条对角线有6种可供选择，当第三条对角线取其中的某一种，则该对角线上的元素-1由元素0代替。

图2 基于滑动矩形窗和准三对角线结构的H b矩阵

3.2 基于准三对角线结构的QC-LDPC码的快速编码算法

基于滑动矩形窗和准三对角线结构的QC-LDPC码的快速编码算法步骤如下：

步骤1将信息比特s和校验比特p分段，每段长度为z，码字序列c如式（11）。

其中，kb=k/z；mb=m/z。

步骤2根据校验矩阵方程H·cT=0得：

其中，cr为˜b2矩阵中r(1)的行值；Zb1(i，j)为矩阵˜b1第i行第j列的置换矩阵。

步骤3由步骤2得到的 p=[p1p2… pmb]，再加上信息比特s，最终得到编码码字c。

在准双对角线结构中，p1的计算式为：

显然，式（12）中的计算量要小于式（14），由此可知，准三对角线结构编码算法的计算复杂度低于准双对角线结构，更适合于硬件实现。表1给出了准三对角线和准双对角线结构编码算法的p1运算量比较，其中LDPC码的码率为1/2、码长为n、扩展因子为z。

表1 两种结构编码算法的p1运算量比较

4 基于滑动矩形窗和准三对角线结构QC-LDPC码的仿真

采用快速迭代编码算法，BPSK调制，LLR BP译码[14-15]，迭代次数20次，在AWGN信道下对基于滑动矩形窗和准三对角线结构的QC-LDPC码进行仿真，同时和IEEE802.16e标准QC-LDPC码进行比较。

表2给出了m=6，k取不同的值时使用滑动矩形窗构造QC-LDPC码的参数。从中可以看到码率范围从1/7到5/8，且码长按照不同的步长从42到816变化，码长和码率的变化非常灵活，因此可以满足自适应传输系统的需求。

表2 滑动矩形窗构造QC-LDPC码的参数

图3是在相同码率的情况下，不同度数的基本校验矩阵在对角线优化方法前后的性能对比。可以看出在度数不大于6时，优化后的性能改善不大，但当度数大于6时，对角线优化方法的性能优势明显，QC-LDPC码的误码率性能得到较大的提高。

图3 对角线优化前后的误码率性能比较

表3给出了滑动矩形与文献[13]和802.16e标准QC-LDPC码的各项指标的数据比较。可以看出，802.16e标准的LDPC码的码率只有4种，码长以96为步长从576到2 304共19种，文献[13]的码率从1/4到3/4，最小码长为336，步长为4到9。而滑动矩形窗QC-LDPC码，其码率没有限制，且最小码长为42，步长为4，结构化的设计和改进的算法，可实现码率、码长的灵活变化，提高可用QC-LDPC码的范围，更适合于变速率的自适应传输系统。

表3 滑动矩形窗与802.16e标准QC-LDPC码的参数对比

根据图2中的Hb矩阵，选择不同的第三条对角线，对构造的QC-LDPC码进行误码性能分析。其中仿真帧数为300，码长为1 152，码率为1/2，扩展因子z=64，仿真结果如图4。可以看出，第三条对角线选择II或III的误码性能最好，VI的误码性能最差，这是由于第三条对角线的不同，得到的LDPC码的度分布也不同。随着码长的增加，准三对角线结构的第三条对角线的选择更多，度分布的变化更灵活，接近好的度分布的机会也越大，因此准三对角线结构具有更加的灵活性。

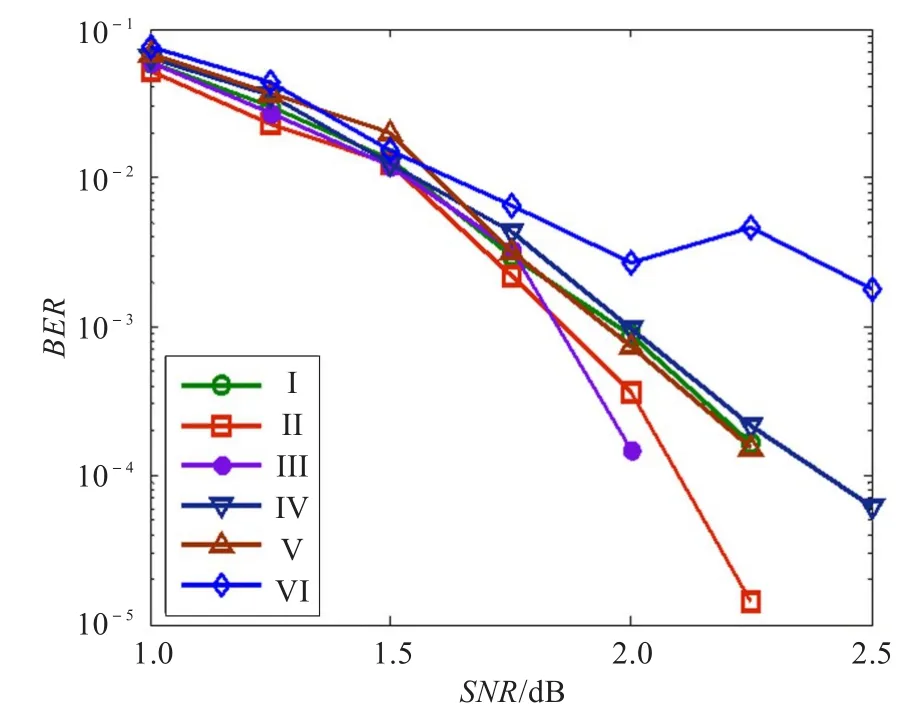
图4 不同的第三条对角线的QC-LDPC码误码性能

基于滑动矩形窗和准三对角线结构QC-LDPC码和IEEE802.16e标准LDPC码在不同码长情况下的误码性能比较结果如图5。其中，码长取576、960和1 152三种，仿真帧数分别为1 000、500和300，码率为1/2。可以看出，在码长为576时，基于滑动矩形窗和准三对角线结构的QC-LDPC码的误码性能较差，但在码长为960和1 152时，其性能接近于802.16e标准LDPC码，甚至在高信噪比时，其性能还要好于标准LDPC码。

5 结束语

图5 基于滑动矩形窗和准三对角线结构QC-LDPC码和802.16e LDPC码的误码性能比较

本文提出的基于滑动矩形窗和准三对角线结构的QC-LDPC码的构造方法以及快速迭代编码算法，设计简单且易于硬件实现，具有更低的计算复杂度，误码性能在低信噪比时接近802.16e标准QC-LDPC码，在高信噪比时甚至要好于802.16e标准QC-LDPC码，并且可实现码率、码长的灵活变化，提高可用QC-LDPC码的范围，更适合于变速率的自适应传输系统。

[1]Fossorier M P C.Quasi-cyclic low density parity check codes from circulant permutation matrices[J].IEEE Trans on Info Theory，2004，50（8）：1788-1793.

[2]Tanner R M.A recursive approach to low com p lexity codes[J].IEEE Trans on Info Theory，1981，27（5）：533-548.

[3]Zhang Fan，Mao Xuehong，Zhou Wuyang.Girth-10 LDPC codes based on 3-D cyclic lattices[J].IEEE Trans on Vehicular Technology，2008，57（2）：1049-1060.

[4]Kim S，Chung H.On the girth of Tanner（3，5）quasicyclic LDPC codes[J].IEEE Trans on Info Theory，2006， 52（4）：1739-1744.

[5]Wang Yige，D raper S C，Yedidia J S.Hierarchical and high girth QC LDPC codes[J].IEEE Trans on Info Theory，2013，59（7）：4553-4583.

[6]Kang J，Fan P，Cao Z.Flexible construction of irregular partitioned LDPC codes with low error floors[J].IEEE Communications Letters，2005，9（6）：534-536.

[7]M yung S，Yang K.Lifting methods for quasi-cyclic LDPC codes[J].IEEE Communications Letters，2006，10（6）：489-491.

[8]Sharon E，Lisyn S.Constructing LDPC codes by error m inim ization progressive edge grow th[J].IEEE Trans on Communications，2008，56（3）：359-368.

[9]彭立，朱光喜.QC-LDPC码的置换矩阵循环移位次数设计[J].电子学报，2010，38（4）：786-790.

[10]郭锐，胡方宁，刘济林.一种低差错平底线性复杂度的QC-LDPC码构造方法[J].电路与系统学报，2011，16（6）：87-93.

[11]韩辉，刘磊，詹磊.一种码率码长灵活变化的QC-LDPC码[J].无线通信技术，2009，18（4）：1-4.

[12]Xu Y，Wei G.On the construction of quasi-systematic block-circulant LDPC codes[J].IEEE Commun Letters，2007，11（11）：886-888.

[13]Wai M，Francis C，Chi K.A class of QC-LDPC codes with low encoding complexity and good error performance[J].IEEE Commun Letters，2010，14（2）：169-171.

[14]张民强，李存华.基于可信度信息的改进加权比特翻转算法[J].计算机工程与应用，2012，48（31）：112-114.

[15]佟宁宁，赵旦峰，吴宇平.一种改进的LDPC码的EBF构造算法的研究[J].计算机工程与应用，2012，48（23）：32-35.

WANG Hanxin,WANG Fang,SU Kaiyou,ZHU Cuitao

College of Electronics and Information Engineering,South-Central University for Nationalities,Wuhan 430074,China

QC-LDPC codes with slide rectangular window and quasi tri-diagonal structure are proposed, the more flexible code lengths and code rates of QC-LDPC codes are expanded by using slide rectangular window in the base check matrix, the degree distribution is optimized by the optimal diagonal method. The error floors of QC-LDPC codes are lower by using quasi tri-diagonal structure which appropriately selects the location of the third diagonal in the base check matrix to partly eliminate variable nodes of degree-2. Simulation results show the proposed QC-LDPC codes can not only flexibly expandthe code lengths and code rates but also reduce the encoding complexity and improve the BER performance compared to quasi dual-diagonal structure in IEEE 802. 16e QC-LDPC codes, they are available and suitable for the adaptive transmission systems and hardware implementation.

Quasi-Cyclic Low-Density Parity-Check（QC-LDPC）codes; diagonal structure; degree distribution; encoding complexity

WANG Hanxin,WANG Fang,SU Kaiyou,et al.QC-LDPC codes with slide rectangular window and quasi tri-diagonal structure.Computer Engineering and Applications,2014,50（17）：186-190.

A

TP301

10.3778/j.issn.1002-8331.1310-0449

国家自然科学基金（No.61072075）；中央高校基本科研业务费专项资金重点项目（No.CZZ13001）；湖北省自然科学基金（No.2013CFB448）。

汪汉新（1966—），男，副教授，研究方向：信息与编码、无线通信技术。E-mail：w anghx8888@163.com

2013-11-01

2014-02-20

1002-8331（2014）17-0186-05

CNKI网络优先出版：2014-03-03,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1310-0449.htm l