基于混合蛙跳算法的协同空战火力分配

张凯，周德云，潘潜

西北工业大学电子信息学院，西安 710129

基于混合蛙跳算法的协同空战火力分配

张凯，周德云，潘潜

西北工业大学电子信息学院，西安 710129

针对超视距多机协同空战中的火力分配（WTA）问题，建立了协同空战火力分配的数学模型，提出了采用混合蛙跳算法（SFLA）来求解协同空战火力分配问题，根据无约束化的编码方式，结合交叉、变异的遗传操作，提高了算法的收敛速度以及全局搜索能力，能有效避免陷入局部最优。仿真结果表明，所提出的混合蛙跳算法在解决协同空战火力分配问题中具有高效可行性。

协同空战；火力分配；混合蛙跳算法；遗传算子

1 引言

随着机载火控系统的快速发展，超视距协同空战已成为现代空战的主要形式，火力分配作为必不可少的决策支持，一直是研究的热点[1]。Lloyd和W itsenhausen已证明了WTA问题是NP完全问题[2]，针对该问题，目前已有多种算法，如拍卖算法[3]、混合粒子群算法[4-6]、蚁群算法[7-8]、遗传算法[9]等，以上算法均已应用于火力分配并取得显著的成果。

在以上研究的基础上，本文提出了一种混合蛙跳算法求解协同多目标空战决策问题。作为一种新的仿生学智能优化算法，蛙跳算法结合了基于模因进化的模因演算法（M emetic A lgorithm，MA）和基于群体行为的粒子群算法（Particle Swam optimization，PSO）的优点，调整参数少，收敛速度快，全局寻优能力强[10]。仿真结果表明了该算法在解决协同多目标空战决策问题中的有效性。

2 协同空战火力分配数学模型

设在多机系统攻击多目标的超视距空战中，我方的空战编队有n架飞机，每架飞机载有ki枚导弹，共有k1+k2+…+kn=k枚导弹；所要攻击的敌机数目为m架，每架敌机的威胁系数为ωh，h=1，2，…，m。其中第i枚导弹对第j架敌机的毁伤概率为pij，i=1，2，…，k，j=1，2，…，m。

引入火力分配的决策矩阵[11]：

xij为决策变量，xij=1表示分配了第i枚导弹攻击第j架敌机，否则xij=0。

则协同空战火力分配数学模型可描述为：寻求一组解X，满足以下目标函数和约束条件：

目标函数：

其中，第一个约束条件表示一枚导弹只能用于打击一个目标，第二个约束条件表示所能使用的导弹数量不超过k个。

3 蛙跳算法

蛙跳算法（Shuffled Frog Leaping A lgorithm，SFLA）由Eusuff和Lansey为解决组合优化问题于2003年提出[12]，作为一种新的仿生学智能优化算法，该算法具有调整参数少、收敛速度快、有效避免局部最优解的特点。目前混合蛙跳算法主要应用于解决多目标优化问题，如资源分配、作业调度、流程安排等工程实际应用问题[13-14]。

作为一种后启发式群体进化算法，蛙跳算法的思想是：湿地中的一群青蛙通过寻找不同的石头进行跳跃去找到食物较多的地方。青蛙具有自己的文化，每只青蛙的文化被定义为问题的一个解，个体之间通过文化的交流实现信息的交换。湿地的整个青蛙群体被分为不同的子群体，在子群体中的每个个体通过自己的文化影响着其他个体，也受其他个体的影响，并随着子群体的进化而进化，执行局部搜索策略。当子群体进化到一定阶段以后，各子群体之间再进行文化的交流实现子群体间的混合运算。重复上述过程，直到满足设置的截止条件为止。

SFLA算法的数学模型可以表示为：首先，随机初始化生成解空间为S维、规模为N的初始种群P= {X1，X2，…，XN}，第i只蛙表示问题的一个解Xi=[xi1，xi2，…，xiS]。将初始种群中蛙的个体按适应值降序排列，并将种群中具有最优适应值的个体记为Xg。然后将整个种群分为m个模因组，每个模因组含有n只蛙，即N=n×m，分配方法为：第1只蛙分入第1模因组，第2只蛙分入第2模因组，…，第m只蛙分入第m模因组，第m+1只蛙分入第1模因组，…，依次类推。第k个模因组的蛙的集合Ak可表示为[15]：

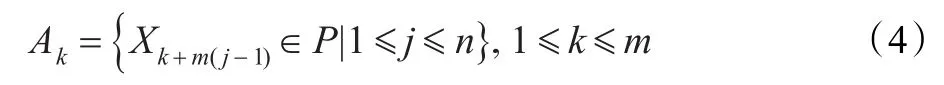
将每个模因组中的最优适应值个体和最劣适应值个体记为Xb、Xw，然后在每个模因组中根据蛙跳规则执行局部搜索策略：

式中，rand()表示（0，1）之间的随机数，Dmax表示蛙每次跳跃步长的最大值。在经过更新后，如果得到的优于原来的Xw，则取代原模因组中的Xw；如果没有改进，则用Xg取代Xb，再按式（5）与式（6）执行局部搜索过程，如果仍没有改进，则随机产生一个新蛙直接取代原Xw。重复上述局部搜索过程iN次，然后将整个蛙群重新混合并排序和划分基因组，再进行局部搜索，如此反复，直到满足设定的截止条件为止，如适应度达到期望值或达到混合迭代次数im。

4 求解火力分配问题的混合SFLA算法

协同多目标空战火力分配的数学模型作为带有一定约束条件的非线性0-1整数规划问题，若按基本SFLA算法来求解，其步长的速度向量难以表达。故本文在一种无约束化的编码方式上，借鉴遗传算法的交叉、变异思想，采用遗传-蛙跳混合算法来解决空战火力分配问题。

4.1 解的编码

在混合SFLA算法中，对解的位置需要结合实际问题进行编码。本文采用了一种基于实数的编码方式，此编码方式不仅用粒子位置代表一种导弹-目标分配的决策方案，而且还满足模型中所有约束条件的要求，从而实现了原规划问题的无约束转化。

由上述设计第i个载机平台的火力策略空间：

其中，xir∈0，1，…，m;r∈1，2，…，ni。当xir=h时，表示第i个载机平台的第r枚导弹用于摧毁第h个目标，当xir=0时，表示第i个载机的第r个武器单元没有使用。以上是第i个载机平台决策序列的编码，编码长度为ni，其他平台以此类推。

4.2 个体更新策略

首先，选出整个种群中最优适应值个体Pg，每个模因组中的最优适应值个体Pb、最劣适应值个体Pw。然后将Pb和Pw进行交叉操作，比较新产生的两个个体与Pw的适应值，如有比Pw适应度高的个体，就用较优适应值的个体替代Pw。否则用Pg代替Pb与Pw进行交叉操作，如果产生的个体仍不优于Pw，则对Pw进行变异操作，并用产生的新个体直接替代Pw。具体的交叉、变异操作策略如下：

交叉操作：由解的编码方式可知，编码长度等于我机编队的火力单元总数k，所以粒子X与粒子Y均是长度为k的实数序列。生成一个长为k的0-1随机序列，在“1”对应的位置上将粒子X与粒子Y进行交换，“0”所在的位置则不进行操作，从而产生新粒子X'、Y'。

变异操作：变异操作与交叉操作类似，首先生成一个长为k的0-1随机序列，在“1”所在的位置上对粒子X进行变异操作，“0”所在的位置上则不进行操作。

4.3 混合SFLA算法流程

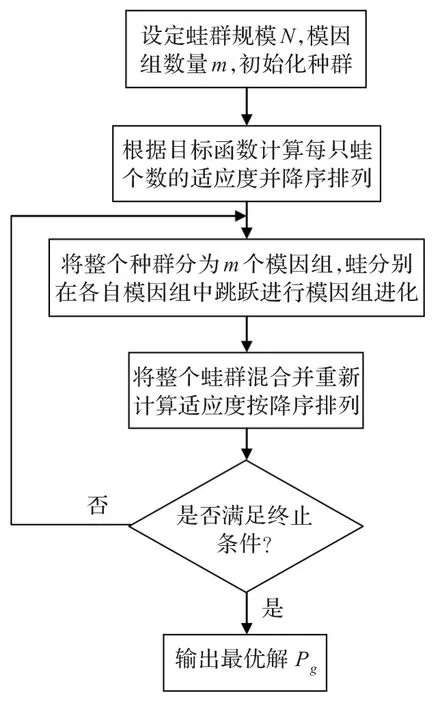
图1 蛙跳算法总流程

5 仿真分析

为了测试混合SFLA算法处理协同多目标攻击空战决策问题的性能，引入文献[4]中所用的作战想定，设我方战机编队与敌机编队在超视距条件下进行空战，我方战机数量为4架，每架飞机上均挂载4枚导弹，共探测到联合攻击区内的10架敌机，我方战机编队采用协同空战战术。

各导弹对各目标的毁伤概率矩阵为：

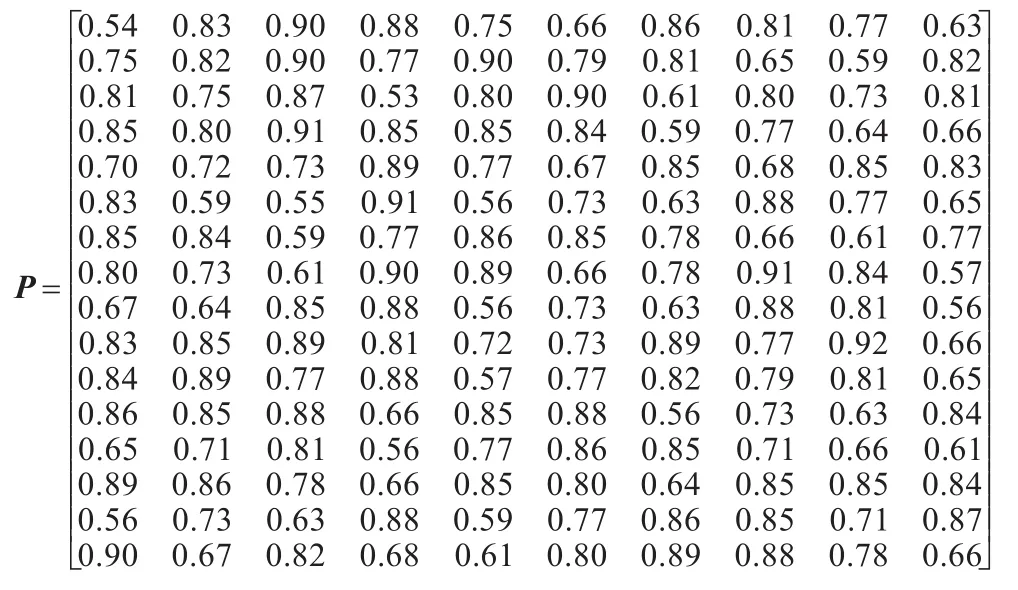
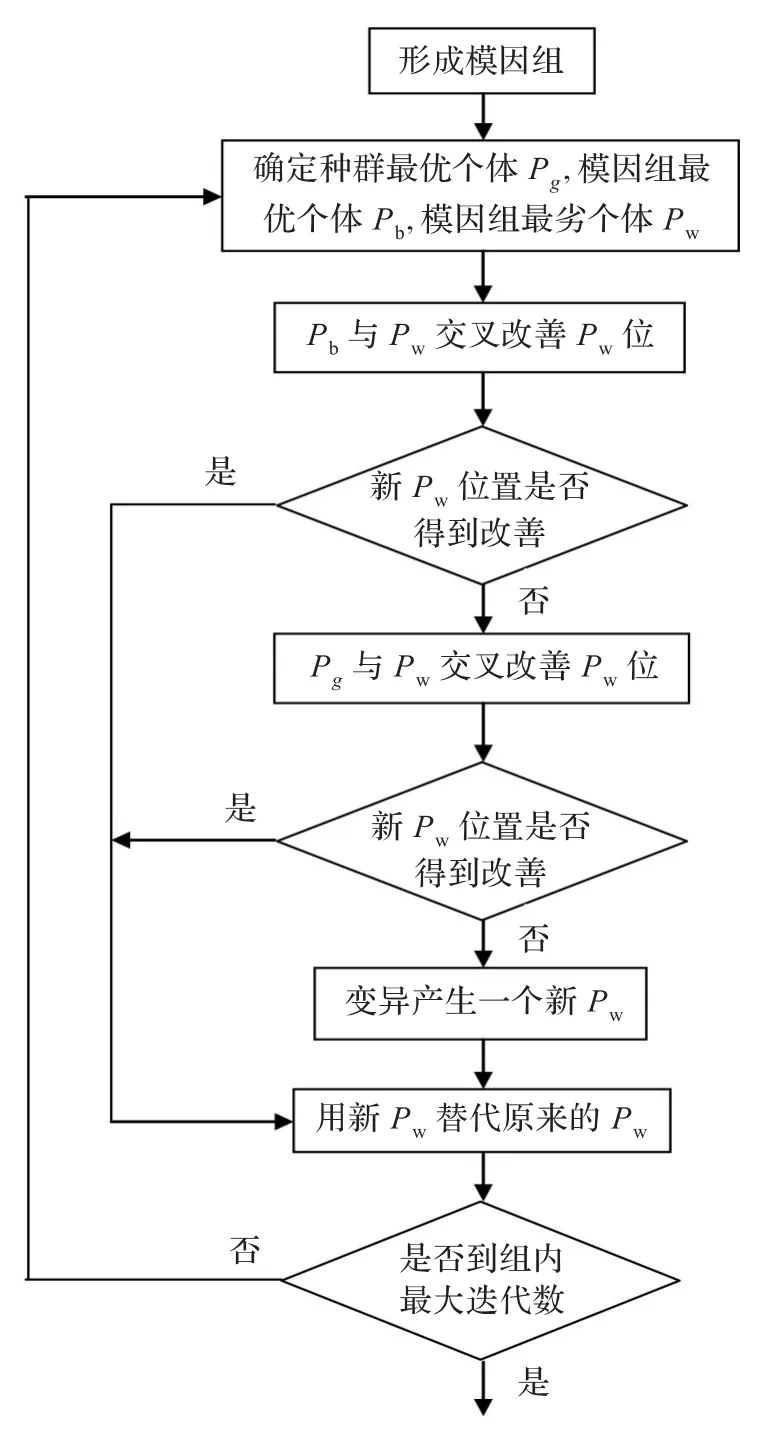
图2 模因组进化流程

各目标的威胁权重矩阵为：

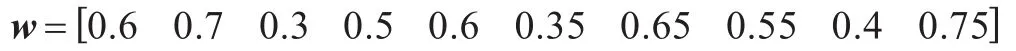
在本文所采用的GA-SFLA算法中，种群规模取为100个，模因组数目为5个，每个模因组规模为20个。在这样的情况下，使用GA-SFLA算法和SA-DPSO算法分别对该火力分配问题进行优化求解。所得的最优适应值变化情况见图3。

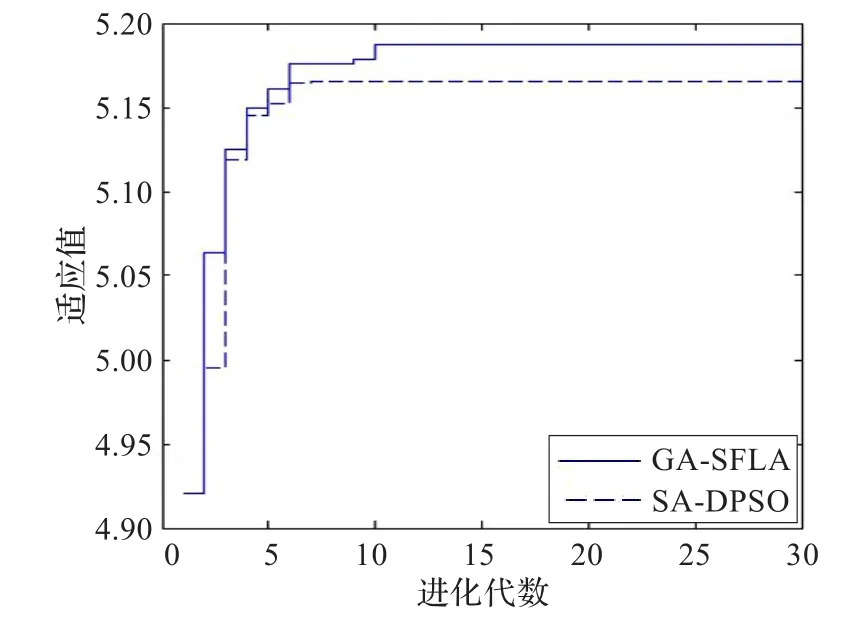
图3 最佳适应值的变化曲线

最优分配情况如下：

通过比较可知，混合SFLA算法不但可以在设定的代数中找到最优解，而且能够有效地避免局部最优。而SA-DPSO算法不仅收敛速度慢于混合SFLA算法，且在迭代过程中会陷入局部最优解。此外，考虑到火力分配的实时性问题，从算法的效率上来看，GA-SFLA的粒子更新只需对每个模因组的最后一个粒子进行操作，将更新后的该粒子根据适应值排序重新插入到模因组中，整个算法具有并行性且设置参数少。而SA-DPSO算法是一种两层的串行结构，DPSO的一次优化结果作为SA的初始种群，SA经M etropolis抽样过程得到的解又成为下一次进化的初始种群，过程复杂且涉及的动态参数较多，不利于大规模问题的快速求解。这说明本文提出的混合SFLA算法在解决协同空战火力分配问题上是快速有效的。

6 结论

本文建立了协同空战火力分配数学模型，引入的编码方式将原模型转化成为无约束优化问题，且不增加问题的复杂性。提出了一种混合SFLA算法对模型进行求解，在求解过程中，充分利用了群智能的信息（种群最优、模因组最优和模因组最劣）和智能算法的个体智能（交叉、变异），且各模因组进化具有高度的并行性，体现了分布式计算的高效率。仿真结果表明，提出的混合SFLA算法是快速有效的。

[1]蔡怀平，陈英武.武器-目标分配（WTA）问题研究进展[J].火力与指挥控制，2006，31（12）：11-15.

[2]Lloyd S P，H S W.Weapons allocations is NP-complete[C]// Proceedings of the 1986 Summer Conference on Simulation，Reno，Nevada，1986.

[3]费爱国，张陆游，丁前军.基于拍卖算法的多机协同火力分配[J].系统工程与电子技术，2012，34（9）：1828-1833.

[4]李俨，董玉娜.基于SA-DPSO混合优化算法的系统空战火力分配[J].航空学报，2010，31（3）：626-631.

[5]陈华东，王树宗，王航宇.基于混合粒子群算法的多平台多武器火力分配研究[J].系统工程与电子技术，2008，30（5）：880-883.

[6]高尚，杨静宇.武器-目标分配问题的粒子群优化算法[J].系统工程与电子技术，2005，27（7）：1250-1253.

[7]罗德林，段海滨，吴顺详.基于启发式蚁群算法的协同多目标空战决策研究[J].航空学报，2006，27（6）：1166-1170.

[8]Gao S.Solving weapon-target assignment problem by a new ant colony algorithm[C]//Proceedings of the 6 World Congress on Intelligent Control and Automation，2008，1：221-224.

[9]杨山亮，黄健，刘洋，等.基于遗传算法的联合火力WTA问题研究[J].计算机仿真，2012，29（3）：61-64.

[10]罗雪晖，杨烨，李霞.改进混合蛙跳算法求解旅行商问题[J].通信学报，2009，30（7）：130-135.

[11]裴兰珍，甘传付，邢波，等.采用改进差分进化算法的防空导弹火力分配[J].计算机工程与应用，2012，48（22）：235-238.

[12]Eusuff M M，Lansey K E.optimization of water distribution network design using the shuffled frog leaping algorithm[J].J of Water Resources Planning and Management，2003，129（3）：210-225.

[13]张敬敏，马丽，李媛媛.求解TSP问题的改进混合蛙跳算法[J].计算机工程与应用，2012，48（11）：47-50.

[14]王亚敏，潘全科，冀俊忠.求解考试时间安排的离散蛙跳算法[J].计算机工程与应用，2009，45（36）：40-44.

[15]崔文华，刘晓冰，王伟，等.混合蛙跳算法研究综述[J].控制与决策，2012，27（4）：481-487.

ZHANG Kai, ZHOU Deyun, PAN Qian

School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710129, China

In view of beyond-visual-range cooperative air combat, the model of Weapon-Target Assignment（WTA）is established,and a mixed Shuffled Frog Leaping Algorithm（SFLA）is proposed to solve the weapon-target assignment problem.Based on an unconstrained encoding, the algorithm combining the cross and mutation of genetic algorithm improves the convergence rate and the seeking ability for the global optimal result so that the local minimum is avoided. The simulation results show that the proposed algorithm is an effective algorithm to solve weapon-target assignment for cooperative air combat.

cooperative air combat; weapon-target assignment; shuffled frog leaping algorithm; genetic operator

ZHANG Kai, ZHOU Deyun, PAN Qian. Weapon-target assignment based on shuffled frog leaping algorithm in cooperative air combat. Computer Engineering and Applications, 2014, 50（17）：263-266.

A

V 247

10.3778/j.issn.1002-8331.1306-0116

航空科学基金（No.20115553021）。

张凯（1988—），男，硕士研究生，研究领域为大系统理论及应用、先进控制理论；周德云（1964—），男，教授，博士生导师；潘潜（1989—），男，硕士研究生。E-mail：zhangkainw pu@mail.nw pu.edu.cn

2013-06-13

2013-10-21

1002-8331（2014）17-0263-04

CNKI网络优先出版：2013-11-27,http://www.cnki.net/kcm s/detail/11.2127.TP.20131127.1511.005.htm l