多项式理论在导弹稳定性能评估中的应用

侯振乾，梁晓庚

西北工业大学自动化学院，西安 710072

多项式理论在导弹稳定性能评估中的应用

侯振乾，梁晓庚

西北工业大学自动化学院，西安 710072

针对线性参数不确定性系统的鲁棒稳定性问题，提出一种新的分析方法，并对其在导弹自动驾驶仪鲁棒稳定性评估中的可行性进行了研究。首先给出线性参数不确定性系统在其特征多项式系数不相关情况下的鲁棒稳定性的充要条件，并通过自适应网格划分算法将此条件与鲁棒D-稳定性理论结合，得到基于多项式理论的评估算法。将算法用于导弹自动驾驶仪鲁棒稳定性评估，得到了不同攻角下导弹在全包线范围内的稳定区域。和只能在离散点进行评估的传统评估方法比较，结果表明提出的算法可以在全包线范围内连续进行评估，从而发现一些隐蔽的不稳定区域。

多项式；网格划分；稳定性能评估；D-稳定性

1 引言

随着技术进步，战斗机越来越多地采用更加先进的气动布局和控制方式，飞行包线不断扩大，机动性能不断提高。这对导弹提出了更高的性能要求，使得导弹的控制系统设计日趋复杂。一方面，需要设计出满足各项技术指标的控制系统；另一方面，在气动参数，传感器或舵机的动态特性发生变化的情况下，需要有效的方法对设计的控制系统进行性能评估，以验证其是否能够满足鲁棒稳定性和鲁棒性能要求。传统的网格评估法在导弹飞行包线内选取离散点并逐个计算这些点处的导弹稳定性，在计算效率和结果可靠性方面显示出不足。针对这一问题，研究人员提出了多种与传统算法相比更具优势的评估算法。基于μ分析的评估算法可以对多回路线性参数不确定性系统进行分析，确定系统保持稳定时不确定参数的最大变化范围；最优化评估算法能够对线性和非线性参数不确定性系统进行鲁棒稳定性分析，并找出导致最坏情况的不确定参数组合[1]。

本文针对线性参数不确定性系统的鲁棒稳定性问题，提出一种基于多项式理论的分析方法，并对其在导弹自动驾驶仪鲁棒稳定性评估中的可行性进行了研究。

2 鲁棒D-稳定性问题

对于线性参数不确定性系统，判断其特征值是否位于复平面内的某个区域D，这就是所谓的鲁棒D-稳定性问题[2]。考虑一个由式（1）描述的线性参数不确定性系统：

其中x(t)∈Rn，A:Rk→Rn×n，π→A(π)是一个关于不确定参数矢量π的连续矩阵方程，Rn是n维系统状态空间，Rk是k维不确定参数空间。

定义1（鲁棒D-稳定性）定义Π⊂Rk（不确定参数空间的一个子空间）和复平面内的开区间D，如果对于所有π∈Π，λi(A(π))∈D，i=1，2，…，n，则由式（1）表示的系统是鲁棒D-稳定的。其中λi(A)表示矩阵A的第i个特征值。

定义1表明，当取不确定参数空间Π中的任意点π，式（1）表示的系统特征值都位于复平面内的区域D时，系统是鲁棒D-稳定的。当D区域与复平面的左半平面重合时鲁棒D-稳定变为鲁棒稳定。

3 多项式理论及评估算法

3.1 多项式理论

线性系统特征多项式的根决定了该系统的稳定性，然而对于含有不确定参数的线性系统，其特征多项式系数是变化的，复平面上的特征多项式根的分布也是不确定的，这也决定了系统的稳定性是不确定的。

用下式表示式（1）中矩阵A(π)的特征多项式：

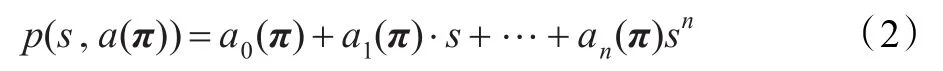
当π在Π内连续变化时，得到一组系数连续变化的多项式，根据鲁棒D-稳定性的定义，当且仅当所有特征多项式的根位于区域D时，由式（2）表示的系统是鲁棒D-稳定的。

对式（2）进行鲁棒D-稳定性分析，首先需要介绍Kharitonov定理[3]，它给出了线性参数不确定性系统鲁棒稳定的充要条件。

考虑下面的多项式：

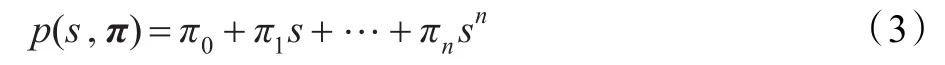
定理1（Kharitonov定理）当且仅当下面四个多项式稳定时，多项式组p(s，Π)={p(s，π)|π∈Π}是鲁棒稳定的。

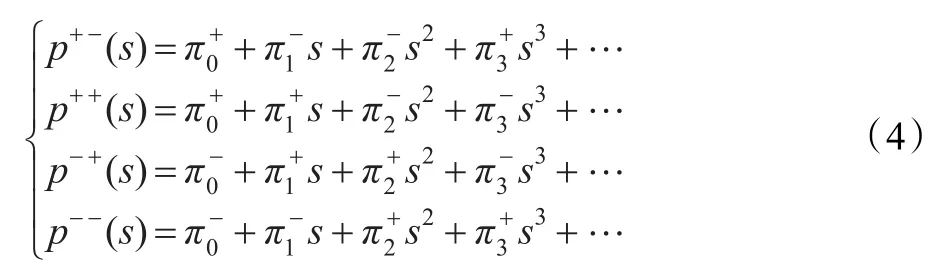
上式称为Kharitonov多项式，系数上标+，-号表示该系数的变化上下界。

Kharitonov定理不适合工程应用，因为它成立的前提是多项式系数线性无关，而在实际情况中，系统特征多项式系数往往受相同参数的影响，例如导弹稳定性导数受攻角，马赫数等参数的影响，说明这些系数本身是互相关联的。Petersen，Bartlett等人进行了很多相关研究[4-13]，改进了Kharitonov的理论，使其能够对系数依赖于一定范围内变化的不确定参数的不确定多项式进行鲁棒稳定性分析。然而这些理论不适用于以下情况：

（1）特征多项式系数和不确定参数之间是非线性关系。

（2）需要确定不确定参数空间中保持系统稳定的区域。

本文利用自适应网格划分算法以及对非线性映射进行线性近似，解决系数线性相关和非线性问题，在此基础上提出了基于多项式理论的评估算法。

3.2 评估算法

文献[14]给出了多项式系数与不确定参数为线性关系时不确定多项式D-稳定的充要条件，文献[15]提出一种算法，可以用线性方程近似非线性矢量方程。在此基础上提出的多项式评估算法的思想就是：

（1）将不确定参数空间进行划分，使得每个子空间内的不确定多项式系数与不确定参数之间为近似线性关系。

（2）对每个子空间进行D-稳定性分析，对满足稳定性的子空间取并集，从而得到整个不确定参数空间内的D-稳定区域。

这样得到的D-稳定区域是一个近似结果，能够保证近似结果向真实结果收敛的关键是当划分的子空间足够小时，用线性方程近似非线性方程产生的误差足够小。

考虑下面的不确定参数空间：

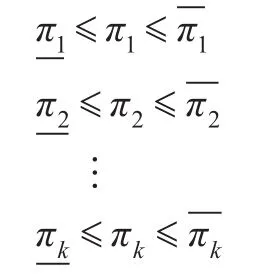
多项式系数和不确定参数之间的非线性映射a(Π)可以用下面的线性映射来近似：

3.2.1 自适应网格划分

自适应网格划分程序将不确定参数空间Π按一定规则分成大小不一的子空间Πi，划分完后在每个子空间内都可以用一个近似线性映射(Πj)代替多项式组a(Πj)。具体流程如图1所示。

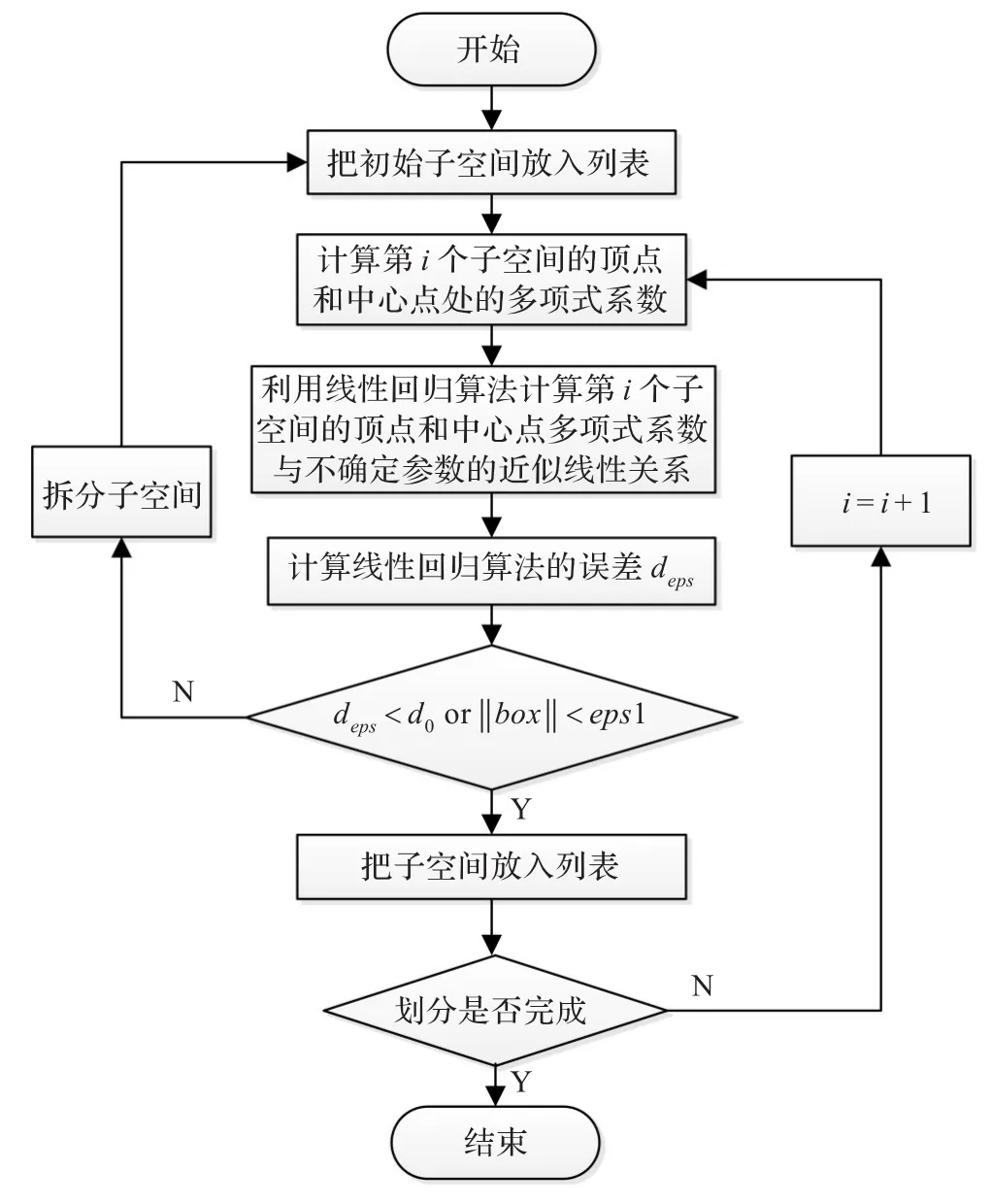
图1 自适应网格划分流程

开始时需要先把不确定参数空间划分成一组初始子空间，初始划分不需要太多，比如当不确定参数是二维时，可以将空间划分为4块初始子空间。然后对每个子空间计算顶点和中点总计2k+1（k是不确定参数的个数）个点处的特征多项式系数，使用线性回归算法计算近似线性映射a(Πj)。记a(Πj)和a(Πj)之间的最大误差为deps，当deps大于最大允许误差d0时，对该子空间进行进一步划分。划分时需设定一个最小边界长度eps1，当子空间边界的最大长度小于eps1时，即使deps＞ d0，也要停止划分程序。

最后将划分完成的子空间放入列表，以进行D-稳定性判断。子空间的划分采用2分法，每次划分产生2k个更小的子空间。

3.2.2 D-稳定区域计算

D-稳定区域计算主要是对前述划分的子空间Πj是否满足评估准则进行判断，并确定满足准则要求的区域。由于利用线性回归算法进行空间划分时存在误差，为了提高评估的可靠性，需要对子空间各顶点是否满足准则进行一致性判断，对一些线性回归误差小，但各顶点处D-稳定性不相同的子空间进行进一步拆分，并设定阈值eps2，eps2应小于eps1，本文取eps2=eps12，当子空间最大边界小于eps2时，如果各顶点处D-稳定性仍不一致，则将此空间归为模糊区域。具体计算流程见图2。

3.3 算法验证

采用一个具体实例来验证上述算法的正确性和有效性，该例子的表达式如下：

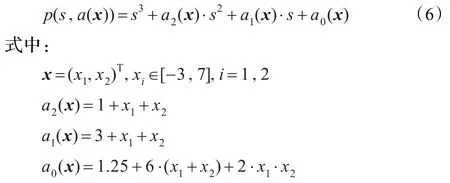
为了验证算法不仅适用于矩形区域，加入限制条件：

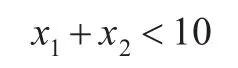
以复平面的左半平面为D-稳定域，利用自适应区域产生算法对上面的多项式进行稳定性分析，以不确定参数x1和x2分别作为纵横坐标，做出不确定参数变化对特征多项式稳定性影响的评估图。图3为执行自适应网格划分算法并对各网格区域执行D-稳定计算后的结果。图中右上方的白色区域满足鲁棒D-稳定性，左下方的深灰色区域不满足鲁棒D-稳定性，浅灰色区域表示这一部分处于临界稳定，减小网格划分阈值eps1，可以减少模糊区域。由图可明显看出不确定参数空间中使系统稳定/不稳定的区域，并且可以找到包含在稳定区域中的不稳定部分。计算结果与实际情况相符，说明算法是有效和准确的。

4 导弹稳定性能评估

本章以BTT导弹纵向模型及自动驾驶仪为评估对象，将高度和马赫数作为不确定性参数，利用多项式评估算法对评估对象在包线内的稳定性能进行评估。研究了不同攻角条件下导弹在包线范围内的飞行稳定性。攻角以2°为间隔在[-10°，20°]内变化。图4～图6分别给出了攻角为-10°，0°和20°时的评估结果，其中白色区域为稳定区域，灰色区域为不稳定区域。

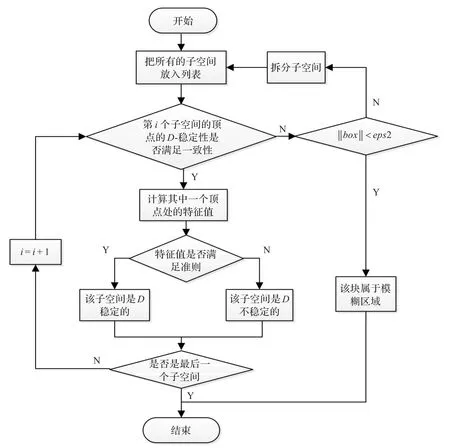
图2 D稳定区域计算流程

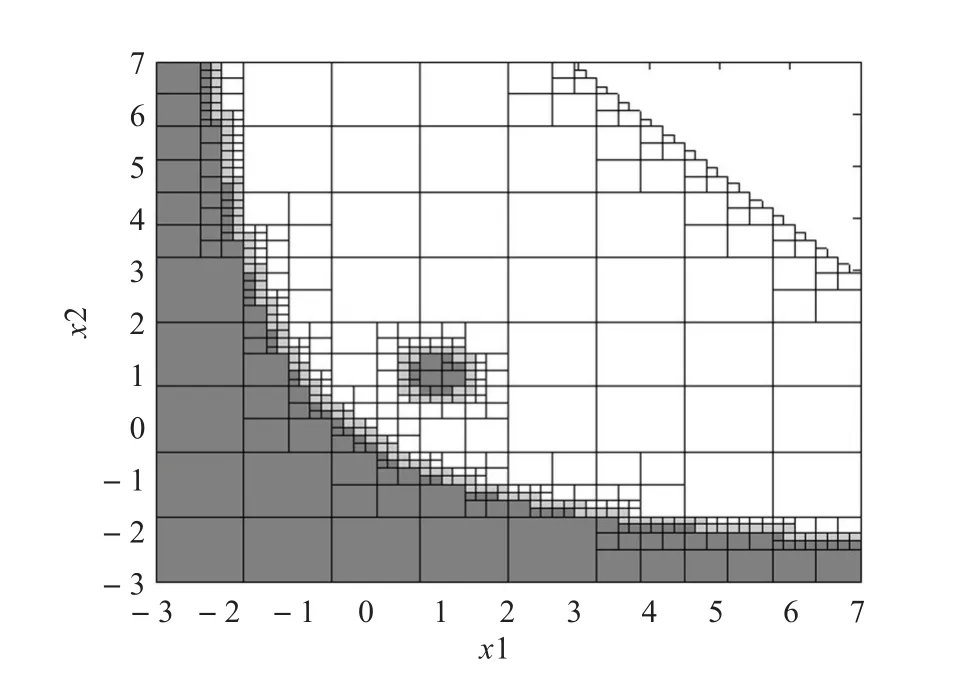
图3 鲁棒D-稳定性计算结果

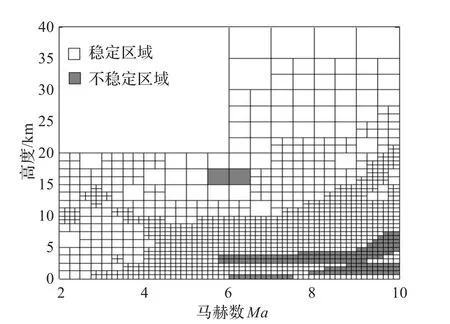
图4 攻角为-10°时导弹在飞行包线内的稳定区域

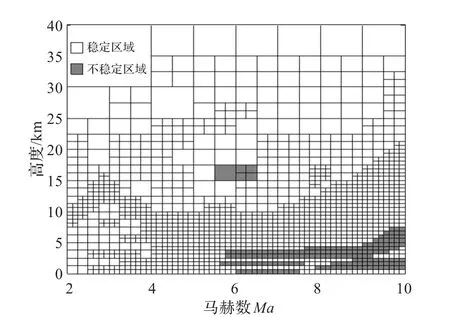
图5 攻角为0°时导弹在飞行包线内的稳定区域

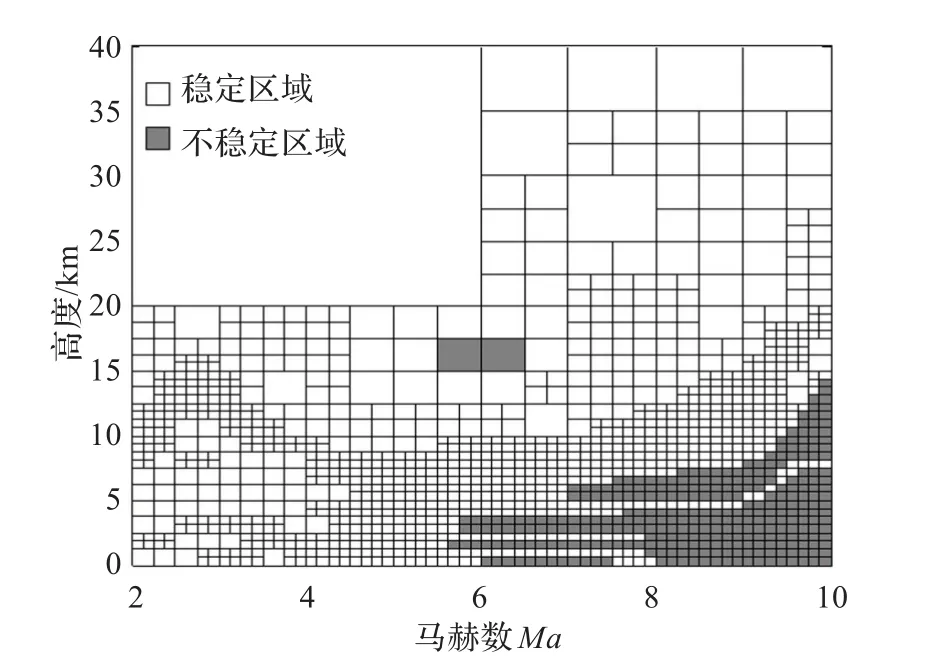
图6 攻角为20°时导弹在飞行包线内的稳定区域

由图可见并经过验证，在马赫数5.5～6.5，高度为15～17.5 km范围内，导弹是不稳定的。由于传统验证方法只对飞行包线内有限的离散特征点的稳定性进行验证，因此没有发现导弹在这一区域内的不稳定性，而基于多项式的评估算法可以在飞行包线内连续进行评估，不会忽略离散点之间的区域，提高了评估的可信度。

5 结束语

传统导弹稳定评估算法只是对离散的飞行状态点进行评估，有可能会出现漏判情况，本文所提算法可以对导弹飞行包线内各飞行状态点连续进行评估，发现隐蔽的不稳定飞行状态，这不仅提高了评估结果的可信度，计算效率也有很大提高。该算法还可以对其他不确定参数，如质心、转动惯量等对导弹飞行稳定性的影响进行评估。在以后的研究中，可以对自适应网格划分算法进行改进，减小线性近似的误差，进一步提高评估结果的可信度。

[1]Fielding C，Varga A，Bennani S，et al.Advanced techniques for clearance of flight control law s[M].[S.l.]：Springer，2002.

[2]Corraro F，Virgilio M.A polynom ial based clearance method[C]//AIAA Guidance，Navigation，and Control Conference and Exhibit，2003.

[3]Kharitonov V.Asymptotic stability of an equilibrium position of a fam ily of systems of linear differential equations[J].Differential Equations，1979，14.

[4]Barm ish B R.A generalization of Kharitonov’s fourpolynom ial concept for robust stability problems with linearly dependent coefficient perturbations[J].IEEE Transactions on Automatic Control，1989，34（2）.

[5]Shang J S.A high-resolution method using adaptive polynom ials for local refinement[C]//48th AIAA Aerospace Sciences Meeting，2010.

[6]Petersen I R.A new extension to Kharitonov’s theorem[J]. IEEE Transactions on Automatic Control，1990，35（7）.

[7]Chapellat H，Bhattacharyya S P.A generalization of Kharitonov’s theorem：robust stability of interval plants[J]. IEEE Transactions on Automatic Control，1989，34（3）.

[8]Hote Y V，Gupta J R P，Choudhury D R.Kharitonov’s theorem and routh criterion for stability margin of interval systems[J].International Journal of Control，Automation，and Systems，2010.

[9]Romanishin I M，Sinitskii L A.On the additive D-stability of matriceson the basis of the Kharitonov criterion[J]. Mathematical Notes，2002，72（2）.

[10]Bartlett C，Hollot C V，Lin H.Root locations of an entire polytope of polynom ials：it suffices to check the edges[J]. Math Contr Signal and Sys，1988，1：61-71.

[11]Sariderely M K，Kern F J.The stability of polynom ials under correlated parameter perturbations[C]//Proc 26th CDC，Los Angeles，CA，1987.

[12]Petersen R.A collection of results on the stability of fam ilies of polynom ials with multilinear parameter dependence，Tech Rep EE8801[R].Australia：University of South Wales，1988.

[13]Pena R S S，Sideris A.A general program to compute the multivariable stability margin for systems with parametric uncertainty[C]//Proceedings of American Control Conference，A tlanta，GA，1988.

[14]Cavallo A，Celentano G，deMaria G.Robust stability analysis of polynom ials with linearly dependent coefficient perturbations[J].IEEE Transactions on Automatic Control，1991：380-384.

[15]Amato F，Verde L.ROBAN：a parameter robustness analysis tool and its flight control applications[C]//3rd IFAC Symposium ROCOND，2000.

HOU Zhenqian, LIANG Xiaogeng

College of Automation, Northwestern Polytechnical University, Xi’an 710072, China

A new method for application to robust stability of linear systems subject to uncertain parameters and applicability to the robustness stability clearance problem of missile autopilot is proposed. First, the necessary and sufficient conditions for robust stability of linear systems subject to uncertain parameters are given for which the characteristic polynomial coefficients are not relevant, then the conditions are combined to robust D-stability theory through adaptive grid generation algorithm, and the polynomial clearance algorithm is obtained. The algorithm is applied to missile stability clearance, the stability region of the whole flight envelope under different angles of attack is obtained. With respect to classical methods, where the analysis is conducted on simple discrete points, the results show that the polynomial based clearancealgorithm allows the flight envelope to be investigated continuously to determine the stable regions and discover hidden unstable regions.

polynomial; grid generation; stability clearance; D-stability

HOU Zhenqian, LIANG Xiaogeng. Polynomial theory applied to stability clearance of missile. Computer Engineering and Applications, 2014, 50（17）：249-253.

A

TJ765.2

10.3778/j.issn.1002-8331.1209-0298

侯振乾（1983—），男，博士研究生，研究方向为导弹控制系统设计；梁晓庚（1960—），男，教授，博导，研究方向为飞行器控制。E-mail：houzhq@yahoo.com.cn

2012-09-26

2012-10-26

1002-8331（2014）17-0249-05

CNKI网络优先出版：2013-01-22,http://www.cnki.net/kcms/detail/11.2127.TP.20130122.1437.005.htm l