SVM在弓网最优压力载荷确定中的应用

时光，陈忠华，郭凤仪，王智勇

辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛 125105

SVM在弓网最优压力载荷确定中的应用

时光，陈忠华，郭凤仪，王智勇

辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛 125105

受电弓滑板的磨损与滑板和接触网导线之间的压力载荷有着密切关系，寻找最优压力载荷使得滑板磨损最小具有重要经济意义。通过对铜基粉末冶金滑板与铜锡导线的对磨实验，得到在不同载流、速度以及变化载荷情况下的滑板磨损情况。针对磨损量不易机理建模的问题，采用支持向量机（SVM）建立了以磨损量作为因变量，以接触压力、滑动速度和接触电流为自变量的回归预测模型，并通过单纯形法确定在特定滑动速度和接触电流条件下的基于滑板磨耗率最低的最优压力载荷，通过算例分析为磨耗率回归预测模型的应用提供参考。

磨损量；支持向量机；最优压力载荷

1 引言

受电弓为电力牵引机车从接触网取得电能的关键电气设备，随着电力机车速度的不断提高，离线率也相应增加，这就使得滑板上的电弧发生得愈加频繁，从而缩短接触线缆的寿命[1]，因此，研究受电弓滑板的磨耗率问题是十分具有经济意义的课题。

在磨损量研究方面，无载流条件系从能量的角度分析磨耗率是目前研究的主流[2]。文献[3]首先提出了接触面上所产生的能量是与摩擦磨损密切相关的观点，之后很多文献利用线性回归的方法得到了磨耗率与摩擦热的近似线性关系[4-8]。而对于载流条件下，接触面上的能量组成表现为复杂性，除了摩擦热还有电流焦耳热和电弧热，其值不易量化。影响磨损量的因素主要有接触压力、接触电流和电力机车的运行速度等，而这些因素又具有交互作用，影响摩擦磨损[9-11]。而载流条件下存在特定的接触压力使得磨耗率最小[12-13]，这就为电力机车在特定接触电流和运行速度条件下的最优压力载荷的研究提供了依据。

本文首先根据实验数据采用支持向量机建立了以磨损量作为因变量，以接触压力、滑动速度和接触电流为自变量的回归预测模型；在此基础上，通过单纯形法，进行最优载荷的求解；最后通过算例分析为所得回归预测模型的实际应用提供参考。

2 实验步骤

2.1 实验材料

导线材料采用铜锡合金导线，截面积为120 mm2，铜基粉末冶金滑板的性能参数如表1。

表1 滑板材料性能参数

2.2 实验条件

所有的测试均是在实验室环境中进行的，滑板表面加入石墨润滑剂。法向压力载荷取值30 N、40 N、50 N、60 N、70 N、80 N和90 N，通过改变砝码桶中的砝码来实现；电流取值100 A、150 A、200 A、250 A和300 A；速度取值40 km/h、60 km/h、80 km/h、100 km/h、120 km/h和140 km/h。其中磨损量定义为滑板相对于接触导线滑动104km的质量损失，即磨耗率，单位为g/104km。

2.3 最优载荷

实验主要研究弓网模拟系统在各种工况下，滑板与导线的磨损与载荷大小之间的变化关系。图1表示运行速度为100 km/h，磨损量与压力载荷和电流的关系图。

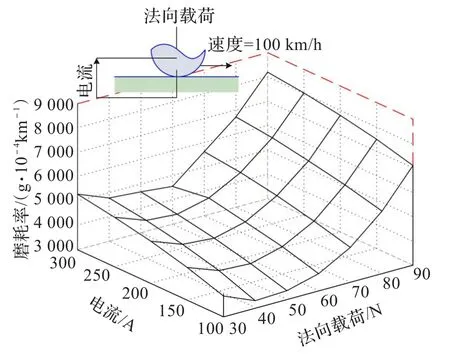
图1 速度100 km/h时磨耗率变化特性曲线

分析图1可知，压力载荷的大小将直接影响载流摩擦的性能。对于载流摩擦副磨损接触表面而言，当法向载荷达到某一阈值时，滑板的磨耗率表现为最小，该阈值即为最优压力载荷。

3 支持向量机回归模型

SVM是基于统计学习理论的VC维理论和结构风险最小化原则，其在小样本应用上更具有优势。本文采用的SVM的拓展机制，即支持向量回归（Support Vector Regression，SVR）的方法。用SVR建立回归预测模型，其基本思想是通过一个非线性映射φ，将回归样本数据x映射到高维特征空间G中，并且在这个空间中进行线性回归。给定样本数据{xi，zi}，i=1，2，…，l，其中xi∈Rm，zi∈R为期望值，l为样本总数。SVR采用下式来估计函数：

对应优化目标为：

式（3）中，C为惩罚因子，实现在经验风险和置信风险的折中；ξi，为松弛因子；ε为损失函数。根据优化条件可以得到支持向量回归机的对偶问题：

式（5）中，Qij=K(xi，xj)=Φ(xi)TΦ(xj)，最终，得到支持向量机的回归函数为：

3.1 实验数据预处理

实际应用的弓网系统虽然是在高速、大电流的条件下，但运行速度和接触电流都在一定的范围内，为了加快收敛速度，故对SVR模型的训练数据采用归一化的预处理方式[14]。本文采用如下归一化映射：

式（8）中，x，z∈Rn，xmin=m in(x)，xmax=max(x)，zi∈[0，1]，i=1，2，…，l。

3.2 参数分析

在核函数的选择方面，有线性核函数、多项式核函数、径向基核函数和感知器核函数等，本文采用径向基核函数，即

参数对回归的影响分析如下：

（1）惩罚参数C使得模型复杂度和训练误差取一个折中，参数C过小，回归模型容易出现“欠学习”现象，而太大又会出现“过学习”，都将严重影响回归模型的泛化能力。

（2）参数ε控制着不敏感带的宽度，影响着支持向量的数目。ε值选得太小，回归估计精度高，但支持向量数增多，ε值选得太大，回归估计精度降低，支持向量数减少，支持向量机的稀疏性大。

（3）径向基参数γ决定了样本数据的分布或范围特性。

因此，在标准支持向量机中，参数C、ε和γ通过不同的方式控制着模型的复杂度和泛化能力，针对模型参数的选择已有多种方法，各有优缺点，本文采用遗传算法对其进行优化，其评价优劣的标准是在K折-交叉验证[15]意义下的均方差（MSE）：

3.3 参数优化

支持向量机算法应用于具有小样本特征的实际问题时是否能获得到良好的效果，取决于能否成功地设置该算法的关键参数[16]，本文采用遗传算法（GA）对参数C、ε和γ进行优化，遗传算法采用20位二进制编码，种群规模100，进化代数为100代，交叉概率0.7，变异概率0.05，K取5。基于遗传算法的SVR回归算法流程如图2所示。

图2 基于GA的SVR回归流程图

优化后，参数C=76.06，ε=1.39×10-2，γ=0.154，MSE=1.53×10-4。为了对比SVR的回归和泛化性能，分别训练隐含层神经元取7和10的BP网络。由于BP网络初始的连接权值和阈值对网络训练影响较大，故采用遗传算法对权值和阈值进行优化，训练样本亦采用归一化后的数据。最终得到隐含层神经元取7和10的BP网络的MSE指标分别为8.39×10-4和7.15×10-4，均比SVR的MSE指标高。电流120 A，速度分别为90 km/h、110 km/h时SVM和BP的泛化能力测试如图3所示，其中实线为实验数据。

由图3可知，SVM具有更好的泛化能力，BP网络隐含层神经元有7提高到10，其泛化性能并没有显著提高。

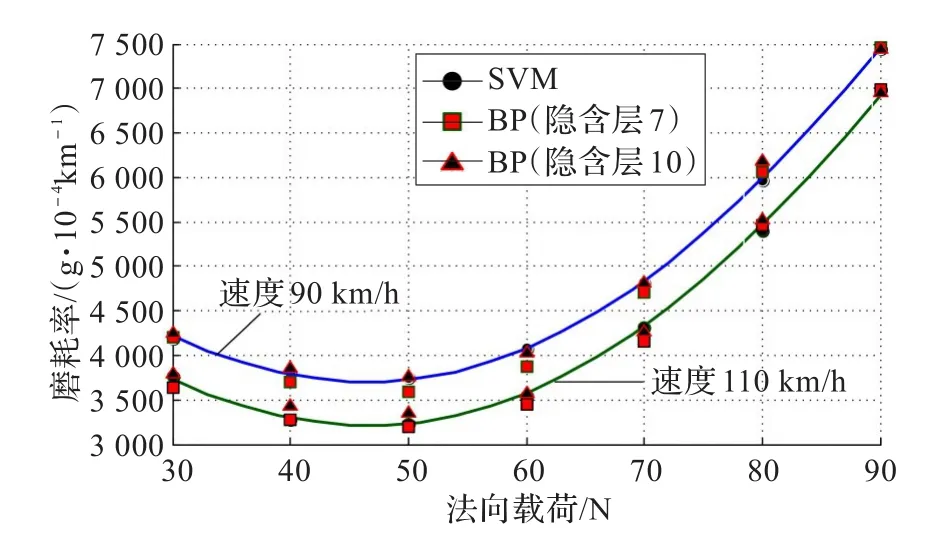
图3 泛化性能

4 基于SVR回归模型的最优压力载荷的确定

基于以上工作，得到了支持向量机的SVR回归模型，但依然无法直接得到特定接触电流和滑动速度下的最优接触载荷。基于SVR回归模型的最优压力载荷优化问题可以描述为：

式（11）中，l为压力载荷，v为运行速度，I为电流。在特定的滑动速度和接触电流情况下，即在点(vi，Ij)都对应一最优的接触载荷lopt使得磨耗率W最小。该问题可以描述为在点(vi，Ij)上，寻找最优的接触载荷lopt的问题，搜索空间相对较小，兼顾优化速度与局部最优值问题，本文采用并行的单纯形法搜索最优压力载荷，其程序流程图如图4所示，n=5，最优压力载荷以及其对应的磨耗率分别见表2。

图4 单纯形法程序流程图

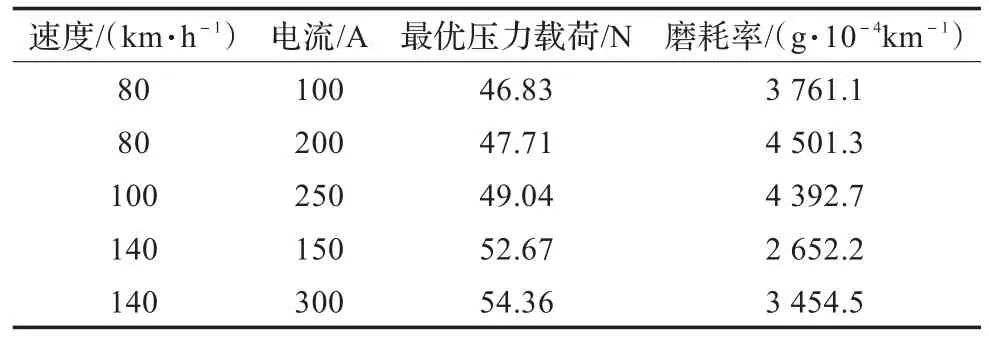
表2 部分最优压力载荷

5 算例分析

电力机车不总运行于同一工况下，运行速度和载流的分布情况易通过统计方法得到，本章将支持向量机回归模型用于计算符合某统计规律工况下的最优法向载荷。设速度V和电流I，二维随机变量(V，I)的概率密度函数为φ(v，i)，则使磨耗率最小的问题转化为：

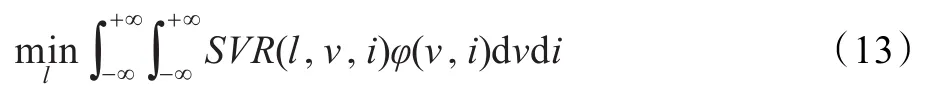
lopt为最优法向载荷的必要条件为：

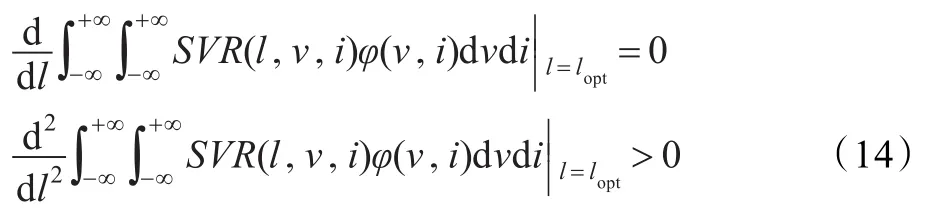
假设(V，I)～N(μ1，μ2，，ρ)，其中μ1=90，μ2=200，σ12=25，σ22=16，ρ=0.1，由于训练数据范围为式（12），利用式（13），求解最优法向载荷的问题可近似转化为：

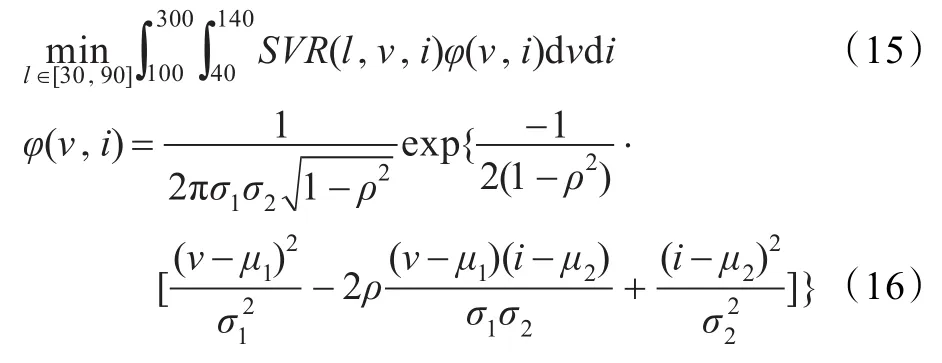
由于SVR(l，v，i)并非解析表达式，故取一系列稠密的载荷点{l1，l2，…，lN}，lopt为：

采用数值积分的方法得lopt=49.2 N。

6 结论

本文首先进行了铜锡导线和铜基粉末冶金滑板的载流摩擦实验，获得了接触压力、滑动速度和接触电流对滑板磨耗率的影响关系数据；然后针对目前对高速载流条件下磨损量模型研究方面的不足，应用支持向量机结合遗传算法建立了以速度、压力和电流作为自变量的SVR回归模型，并通过单纯形法得到了在特定滑动速度和接触电流条件下的基于滑板磨耗率最低的最优接触压力，通过算例分析为进一步的应用研究提供参考。

[1]Buhrkall L.DC components due to ice on the overhead contact w ire of AC electrified railways[J].Electron Mater Lett，2005，8（8）：380-389.

[2]Jahangiri M，Hashempour M，Razavizadeh H，et al.A new method to investigate the sliding wear behaviour of materials based on energy dissipation：W-25 w t%Cu composite[J].Wear，2012，274：175-182.

[3]Czichos H.Tribology：a systems approach to the science and technology of friction lubrication and wear[M].Netherlands：Elsevier Scientific Publishing Company，1978.

[4]Fouvry S，Kapsa P H.An energy description of hard coatings wear mechanism s[J].Surf Coat Technol，2001，138：141-148.

[5]Fouvry S，Liskiew icz T，Kapsa P H，et al.An energy description of w ear mechanisms and its applications to oscillating sliding contacts[J].Wear，2003，255：287-298.

[6]Fouvry S，Paulin C，Liskiew icz T.Application of an energy w ear approach to quantify fretting contact durability：introduction of a wear energy capacity concept[J].Tribol Int，2007，40：1428-1440.

[7]Colaco R，Gispert M P，Serro A P，et al.An energy-based model for the wear of UHMWPE[J].Tribol Lett，2007，26（2）：119-124.

[8]Zhang X，Lauwerens W，Stals L，et al.Fretting w ear rate of sulphur deficient MoSx coatings based on dissipated energy[J].J Mater Res，2011，16（12）：3567-3574.

[9]Jia S G，Liu P，Ren F Z，et al.Sliding wear behavior of copper alloy contact w ire against copper-based strip for high-speed electrified rail ways[J].Wear，2007，262（7）：772-777.

[10]Wang W G，Dong A P，Wu G N，et al.Study on characterization of electrical contact betw een pantograph and catenary[C]//2011 IEEE 57th Holm Conference on Electrical Contacts，2011：1-6.

[11]Engel T G，Neri J M，Veracka M J.Characterization of the velocity skin effect in the surface layer of a railgun sliding contact[J].IEEE Trans on M agnetics，2008，44（7）：1837-1844.

[12]Zhao H，Barber G C，Liu J.Friction and wear in high speed sliding with and without electrical current[J]. Wear，2001，249：409-414.

[13]Wang Y A，Li J X，Yan Y，et al.Effect of electrical current on tribological behavior of copper-impregnated metallized carbon against a Cu-Cr-Zr alloy[J].Tribology International，2012，50：26-34.

[14]Ray S，Roy S K.Prediction of contact temperature rise between rough sliding bodies：an artificial neural network approach[J].Wear，2009，266：1029-1038.

[15]Duan K，Keerthi S，Poo A.Evaluation of sim ple performance measures for tuning SVM hyperparameters[J]. Neurocomputing，2003，51：41-59.

[16]彭光金，司海涛，俞集辉，等.改进的支持向量机算法及其应用[J].计算机工程与应用，2011，47（18）：218-221.

SHI Guang, CHEN Zhonghua, GUO Fengyi, WANG Zhiyong

Faculty of Electrical and Control Engineering, Liaoning Technical University, Huludao, Liaoning 125105, China

There is a close relationship between the wear loss and the pressure between the pantograph slide and the contact wire. Finding the optimal load of the lowest wear of slider makes economic sense. Aiming at the inconvenience of mechanism modeling, Support Vector Machine（SVM）is used to establish the regress model with the dependent variable of wear loss and pressure, velocity and current as the independent variable. The optimal load on the condition of the fixed velocity and current are acquired utilizing the simplex method. A numerical example gives the reference for the further applications of the SVM model.

wear loss; Support Vector Machine（SVM）; optimal load

SHI Guang, CHEN Zhonghua, GUO Fengyi, et al. Application of SVM in determination of optimal load of pantograph.Computer Engineering and Applications, 2014, 50（17）：245-248.

A

TP391

10.3778/j.issn.1002-8331.1308-0071

国家自然科学基金（No.50977040，No.51277090）。

时光（1981—），男，博士，讲师，研究领域为机器学习、电接触理论；陈忠华（1965—），男，教授，研究领域为电接触理论；郭凤仪（1964—），男，教授，研究领域为电机与电器。E-mail：sxysbc@126.com

2013-08-08

2013-10-16

1002-8331（2014）17-0245-04

CNKI网络优先出版：2014-01-15,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1308-0071.htm l