以互信息为度量的一种规则可视化
2014-07-08谢霖铨章恩
谢霖铨,章恩
江西理工大学理学院,江西赣州 341000
以互信息为度量的一种规则可视化
谢霖铨,章恩
江西理工大学理学院,江西赣州 341000
概念格是一种有效的知识表示和知识发现的工具,已被成功应用于许多领域,然而在建格上大多是利用最小支持度以及置信度来进行约简操作,同时利用置信度来进行规则提取。提出以信息论的互信息来构造具有强关联规则的Hasse图,并利用互信息进行规则提取。
强关联规则;概念格;互信息;规则提取;数据挖据
1 概述
自从W ille R教授[1]首先提出形式概念分析以来,形式概念分析已被证明是进行数据分析的有力工具。在应用概念格的过程中,格的构造[2]问题以及规则提取一直是研究的热点。传统的串行可以分为批处理和渐进式构造算法。批处理算法的思想是首先生成所有的概念集合,然后再生成概念之间的直接前驱和后继关系或者是每次生成少量的概念,并将这些概念链接到节点集合中。如:Bordat算法[3]。渐进式算法的思想是先初始化概念格为空,将当前要插入的对象和现有格中的所有的形式概念作交运算,然后采取不同的行动,如Godin[4]等。规则提取有:利用支持度和信任度来提取强关联规则[5]、进行无冗余规则提取[6]、利用内涵缩减[7]进行规则提取[8]及文献[9]等。但却鲜见构成的Hasse图能直接可视化其内部的规则。
本文给出的建格方法是:首先根据形式背景利用FP-TREE的第一次扫描数据库得到项目列表,根据所得的列表进行形式背景的约简,求出形式背景的单元概念的秩,再利用对于概念的内涵和外延作并集和交集的运算,利用互信息的性质进行建格约简操作,得到所需的具有强关联规则的概念格Hasse图,然后利用信息论的互信息M I来进行强关联分析与规则提取。在所得到的Hasee图中可发现其规则是有可视化性。
2 相关概念
定义1[10]在关联规则挖掘中,项集就是项的集合,k项集是包含k项的项集,称为k项集,给定数据库D和最小支持度阈值M in,对于项集(O,A),如果该项集的支持度Sup≥M in,则称该项集为频繁项集。
定义2[11]定义在项目集I和事物数据集D上形如I1⇒I2的关联规则的可信度是指包含I1和I2的事务数与包含I1的事务数之比,简记为Conf(I1⇒I2)即Conf(I1⇒I2)=Sup(I1∪I2)/Sup(I1)。其中,I1,I2⊆I,I1∩I2=φ。
定义3[12]对于频繁项集(O,A),并且对于子节点(O1,A1)。可以得知(O,A)的支持度Sup≥(O1,A1)的支持度Sup。但增加任何一项其支持度Sup<M in,则称(O,A)为最大频繁项集。
根据定义可知:
性质1[13-14]最大频繁项的父节点一定是频繁项集。
性质2[13、14]最大频繁项的子节点一定是非频繁项集。
推论1当某项集节点是非频繁项集时,则包含该节点内涵的所有项集都是非频繁项集。
定义4[1]在形式概念的分析中,概念的形式化背景定义为一个三元组(O,A,R),O代表的是形式对象Object的集合,A代表的是形式属性A ttribute的集合,R代表的是对象O和属性A之间的二元关系Relation。即R⊆O×A。
定义5[11]格L的每一节点为一序偶,记为<X,Y>,其中X是实例集合称为概念的外延,Y是X中所有实例共同具有的属性集合称为概念的内涵,每一序偶相对于关系R是完备的,即
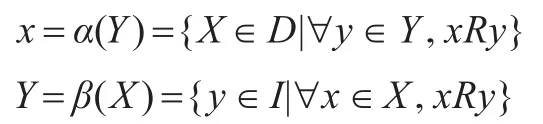
定义6[7]假设有下面的H1=(O1,A1),H2=(O2,A2)∈L,L代表格,如果A1⊆A2或O1⊇O2,则称H1是H2的子概念(节点),H2是H1的父节点。可形式化表示为H1≤H2。
定义7对于概念C=(O,A),称Q为C的量化(Quantitation)概念,其Q是A外延的基数。显然生成的量化概念格和原概念格是同构的。
定义8设(G,M,L)为一形式背景,L(G,M,L)概念格,(A,B)∈L(G,M,L),则(A,B)或者是存在m∈B,使得r(m)=|A|,且(A,B)=({m}+,{m}++),或者为(A,B)的两个直接父节点的交。
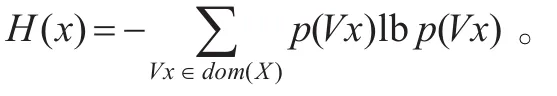
定义10[15]互信息熵:描述了某个变量取值对另一个变量取值的确定的能力。其值越大2个变量间的确定能力越强。2个变量x,y的互信息熵M I(x,y)定义为:
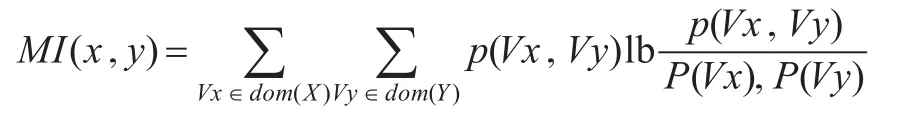
且I(x,y)=H(x)-H(x|y)=H(y)-H(y|x)。
定义11[15]互信息在信息论中是作为一种衡量2个信号关联程度的尺度。后来引申为2个随机变量间的关联程度进行统计描述,可表示成这2个随机变量的概率的函数。假设M I(X,Y)为随机变量X和Y的互信息,则M i(x,y)=lb p(x,y)p(x)p(y),其中p(x,y)=和P(y)分别是x和y独立出现的概率。P(x,y)是x和y同时出现的概率,当M I(x,y)>>0时,表明x和y的关联程度强。M I(x,y)=0时,表明x和y的关联程度弱,它们的同时出现仅属于偶然。当M I(x,y)<<0时,表明x,y互补分布,不存在关联关系。
例1形式背景如表1所示。
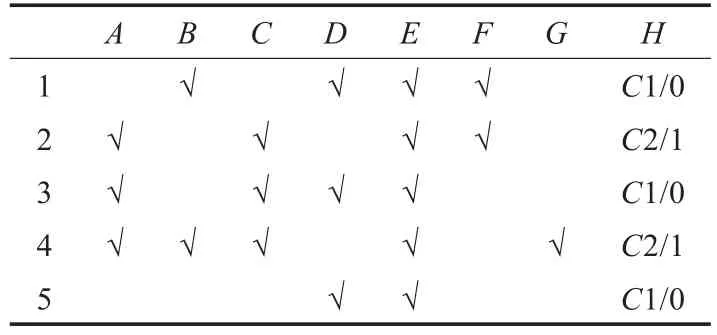
表1 形式背景
则由表1(其中H在分类中表示为C1标签和C2标签,为了对数据的预处理在进行下文的关联规则中将C1替换为0,C2为1)得到的边缘概念根据秩的大小进行排序得到:C1=(E,5),C2=(A,3),C3=(C,3),C4=(D,3),C5=(B,2),C6=(F,2),C7=(G,1)。
3 算法描述及实例验证
本文基于互信息提出强关联规则的建格约简,以互信息的性质可以知道经过约简后的Hasse图的内涵是具有强关联关系,在规则提取中也表现出很大的优势。
3.1 算法描述
输入事务数据集D,最小支持度阈值M in,gram矩阵
输出与D对应的强关联关系的概念格Hasse图
步骤1扫描数据库D一次,收集1频繁项集的集合F和它们的支持度计数Sup,并对F按支持度计数进行降序排序,if Sup≤M in,则删除该项列表DEL得到频繁列表L。
步骤2用形式背景来和删除的列表DEL进行匹配,当匹配成功时形式背景对于该属性进行删除操作。得到新的形式背景H。
步骤3对L进行属性的并集操作得到C,并计算其属性之间的互信息值,为了快捷地进行计算,其互信息值可由gram矩阵给出,当互信息值M I≤0的时候或者其支持度Sup<M in时,可以对其内涵进行约简,且此内涵的父节点都可以进行删除操作。
步骤4根据概念格的分层得到所有的C,直到没有互信息的值小于等于0为止。
步骤5根据所得到各层的属性集并根据偏序关系,生成不带有1项集概念格的Hasse图,并进行连边。
3.2 实例验证
为验证本文算法的有效性,以表1的形式背景分析,设其最小支持度M in的数值为2,可由表1知FPTREE[16]1项集列表如表2及FP-TREE[17]的频繁1项集如表3所示。
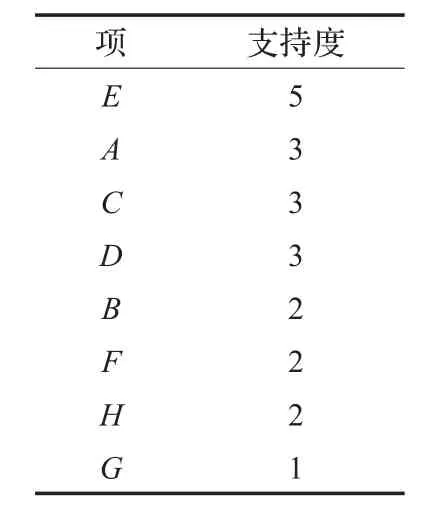
表2 1项集列表

表3 频繁1项集列
所以由删除的列表的概念格属性知形式背景可以转化为表4。
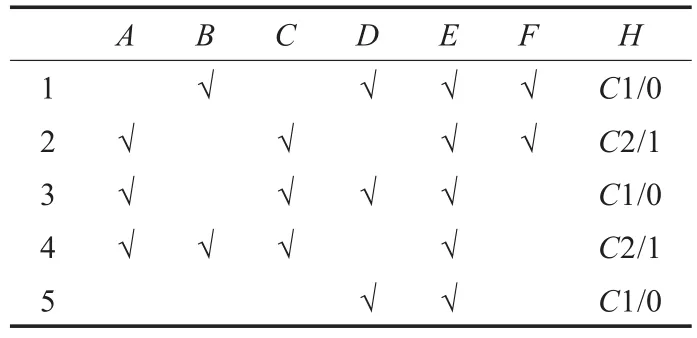
表4 形式背景
则由表4得到的单元概念根据秩的大小进行排序得:C1=(E,5),C2=(A,3),C3=(C,3),C4=(D,3),C5=(B,2),C6=(F,2),C7=(H,2)。再根据步骤3建立Gram概率矩阵如表5。
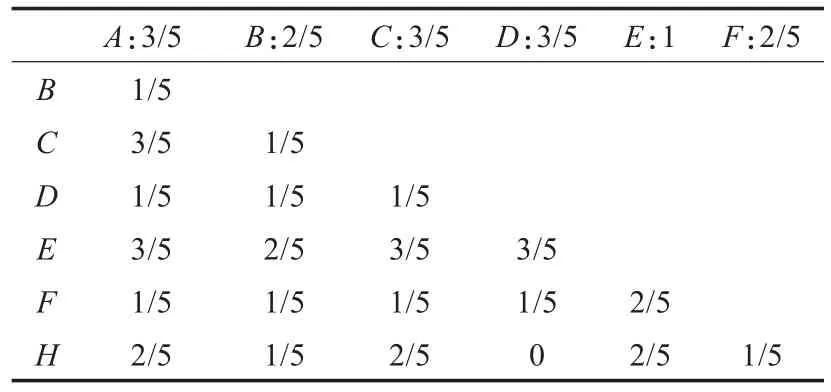
表5 gram矩阵
表5表达的含义是该内涵出现的概率,通过建立gram矩阵,可以满足快捷的算法计算。然后通过约简之后进行内涵并集操作直至结束,根据分层的层次属性知生成以互信息为度量的频繁概念格的Hasse图如图1所示。
4 强关联规则提取
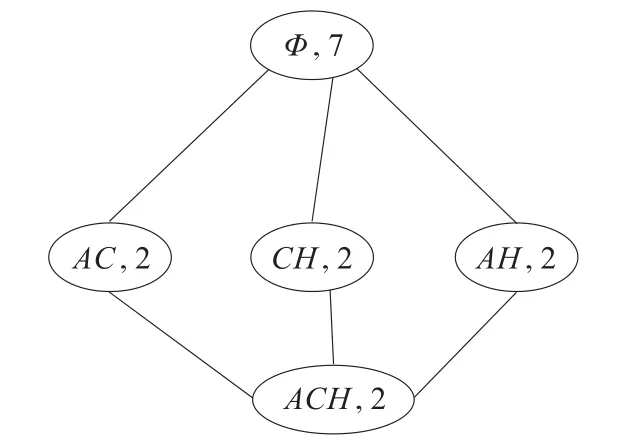
图1 以互信息为度量的Hasse图
本文根据互信息M I来找到最强的关联关系以做更准确的决策,为了更加详细准确地进行强关联规则提取,列出全部的所求得的互信息值如下:M I(A,B)<0,M I(A,C)>0,M I(A,D)<0,M I(A,E)=0,M I(A,F)<0,M I(A,H)<0,M I(B,C)<0,M I(B,D)<0,M I(B,E)=0,M I(B,F)>0,M I(B,H)>0,M I(C,D)<0,M I(C,E)=0,M I(C,F)<0,M I(C,H)>0,M I(D,E)=0,M I(D,F)<0,M I(D,H)=0,M I(E,F)=0,M I(E,H)=0,M I(F,H)>0,M I(AC,H)>0,M I(AH,C)>0,M I(CH,A)>0。根据互信息性质可以直接以叶子节点本文即(ACH,2)作为强关联规则进行规则提取,即有A⇒C,C⇒H,A⇒H,AC⇒H,AH⇒C,CH⇒A由此可根据一个节点推导出所有的规则。
为了能更加详细地体现本文规则提取的准确性,及进行更直观详细细致的比较,在图2给出利用传统方法生成的Hasse图。
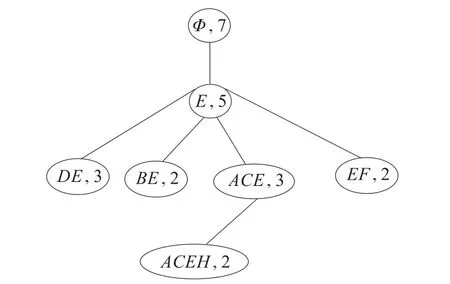
图2 传统hasse图
可以利用文献[7-8]的规则提取发现所得到的规则与本文相同,但本文的方法更加简便,而且更加可视化,只需观察叶子节点即可。
由于互信息表明的是相互之间的关联程度的强弱,所以所得到的M I能体现出它们属性之间规则的相互作用力度。以AC为例。由于M I(A,C)>>0。表明AC之间的关联程度很强。所以可以得到规则A⇒C。又以(A,E)为例,由于M I(A,E)=0所以A和E同时发生是属于偶然事件。根据互信息的公式可以精确地计算出相互属性之间的关联程度,相比与传统的利用置信度得到的关联规则,互信息计算出的值更加精确,可以非常准确地得到关联程度最强的组合。并在分类中可以以最强的关联规则作为类别标签的分类器和进行特征提取。
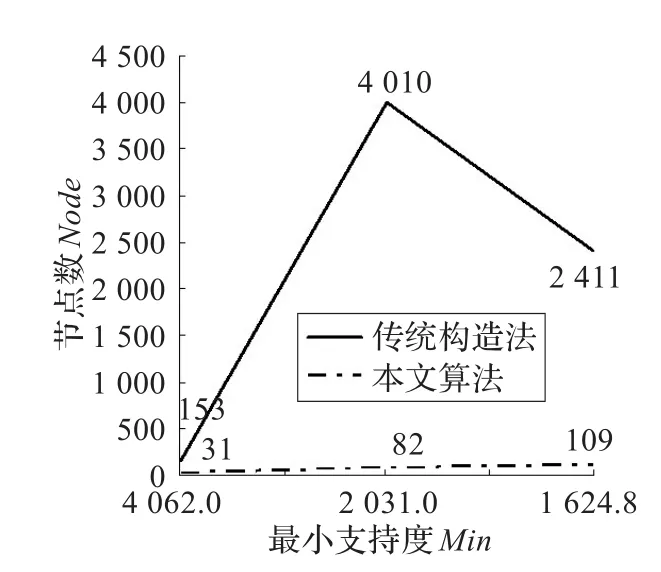
图3 生成格节点数
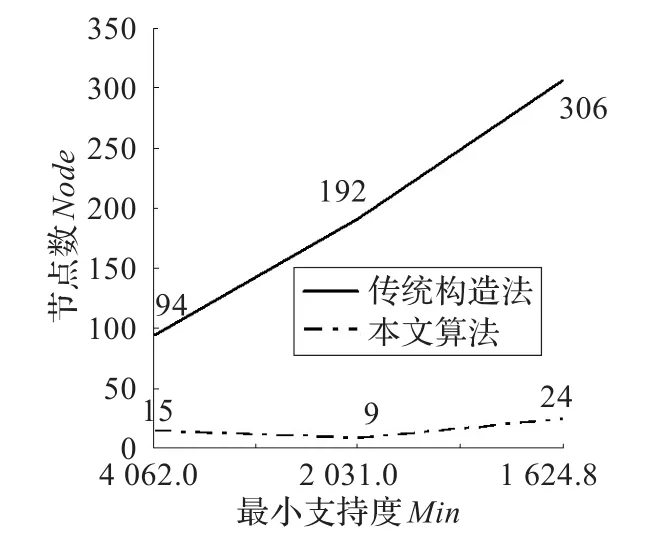
图4 规则提取所需节点数
另外可以从上述的互信息值和Hasse图发现内涵E是必然事件(概率为1),但是其所有的父节点的互信息值都是0,由此根据信息熵的定义可以知道关于内涵E的信息m=-p lb p=-1×0=0。也就是说E的信息量为0,也表明和其他的内涵的关联关系是属于偶然事件。类似于在自然语言处理中,频繁出现的英文单词“the”,“and”或中文词中的“的”,其本身是不携带任何含义的。所以在只进行关联规则提取的过程中是可以直接忽略的,但是因为是必然事件,也应该非常重视。
5 算法实现与比较
为进一步验证该算法的正确性和有效性,使用UC Irvine Machine Learning Repository的mushroom数据集做实验,其下载地址为:https://archive.ics.uci.edu/m l/ datasets/M ushroom,由于原始数据有缺失,本文将其22个特征和所属类别用阿拉伯数字取代,再根据其每一列的特征的平均值所靠近的属性来代替缺失值。在M int15系统下用java运行进行对比,得到的结果如表6。
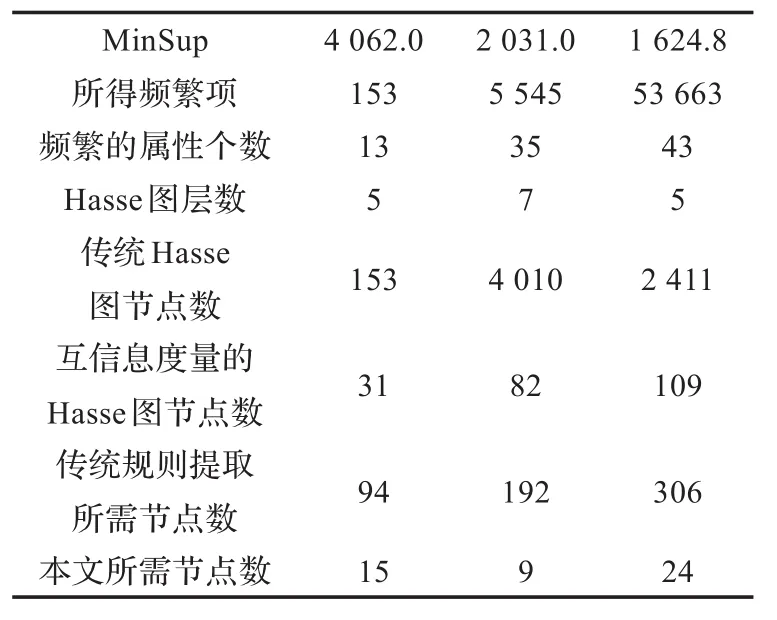
表6 对比数据
其效果对比图如图3、图4所示。由于所建立的Hasse图的方法不一致,本文是以规则可视化为目的,所以生成的Hasse图在数量级的结构不一致。
6 总结
本文利用互信息的特性来进行规则提取,可以快捷精确地得到所包含的规则且可视化。由于本文主要是针对强关联规则进行分析,故互信息的优势得到极大体现。所以当以互信息为度量生成的Hasse图可以利用叶子节点进行规则可视。
[1]胡可云,陆玉昌,石纯一.基于概念格的分类和关联规则的集成挖掘方法[J].软件学报,2000,11(11):1478-1484.
[2]Nourine L,Raynaud O.A fast algorithm for building lattices[J].Information Processing Letters,1999,7(1):199-204.
[3]陈庆燕.Bordat概念格构造算法的改进[J].计算机工程与应用,2010,46(35):33-35.
[4]谢志朋,刘宗田.概念格的快速渐进式构造算法[J].计算机学报,2002,25(2):490-496.
[5]谢福鼎,王照飞.基于概念格的关联规则挖掘[J].计算机工程与应用,2007,43(33):170-172.
[6]刘霜霜,饶天贵,孙建华.基于改进概念格的无冗余关联规则提取[J].计算机工程,2010,36(10):52-55.
[7]智东杰,智慧来,刘宗田.概念格的内涵缩减研究[J].计算机工程与应用,2009,45(1):42-44.
[8]谢志鹏,刘宗田.概念格与关联规则发现[J].计算机研究与发展,2000,37(12):1414-1421.
[9]杨霁琳.一种基于概念格的规则提取方法及其应用[J].计算机科学,2012,39(11A):204-206.
[10]陈湘,吴跃.基于概念格挖掘GIS中的关联规则[J].计算机应用,2011,31(3):686-689.
[11]王慧,王京.FP-Tree上频繁概念格的无冗余关联规则提取[J].计算机工程与应用,2012,48(15):12-15.
[12]余远,钱旭,钟锋,等.基于最大概念的概念格增量构造算法[J].计算机工程,2009,35(21):62-64.
[13]宋余庆,朱玉全,孙志挥,等.基于FP-Tree的最大频繁项目集挖掘及更新算法[J].软件学报,2003,14(9):1586-1592.
[14]姜晗,贾泂,徐峰.基于频繁项集挖掘最大频繁项集和频繁闭项集[J].计算机工程与应用,2008,44(28):146-148.
[15]刘乐乐,田卫东.基于属性互信息熵的量化关联规则挖掘[J].计算机工程,2009,35(14):38-40.
[16]杨云,罗艳霞.FP-Grown算法的改进[J].计算机工程与设计,2012,31(7):1506-1509.
[17]马丽生,姚光顺,杨传健.基于改进FP-tree的最大频繁项集挖掘算法[J].计算机应用,2012,32(2):326-329.
XIE Linquan,ZHANG En
School of Science,Jiangxi University of Science and Technology,Ganzhou,Jiangxi 341000,China
The concept lattice is an effective tool for know ledge discovering and know ledge processing,which has been successfully applied in many fields.How ever,lattice constructions with reduction operation are mostly based on minimum support and degree of confidence.A t the same time,the degree of confidence is used to extract rules.This paper proposes the Hasse diagram with strong association which is constructed by the mutual information of information theory, and extracts rules by mutual information.
strong association rules;concept lattice;mutual information;rule extraction;data mining
XIE Linquan,ZHANG En.Ru les visualization based on Metric of mutual in form ation.Computer Engineering and Applications,2014,50(17):146-149.
A
TP391
10.3778/j.issn.1002-8331.1311-0454
国家自然科学基金(No.61364015)。
谢霖铨(1962—),博士,教授,主要研究方向:序代数、数据挖掘、粗糙集理论及应用;章恩(1990—),硕士,主要研究方向:概念格、机器学习。E-mail:lq_xie@163.com
2013-12-02
2014-04-02
1002-8331(2014)17-0146-04
CNKI网络优先出版:2014-04-21,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1311-0454.htm l
