同一变量排序下的多OBDD合并算法

智慧来

河南理工大学计算机科学与技术学院，河南焦作 454000

同一变量排序下的多OBDD合并算法

智慧来

河南理工大学计算机科学与技术学院，河南焦作 454000

有序决策图（OBDD）是一种用于表示布尔表达式的数据结构，并在许多领域得到了广泛应用。在分布式或者动态环境下，利用已知布尔表达式的OBDD构造目标布尔表达式的OBDD是一个决定实际问题解决效率的关键问题。基于Shannon分解原理提出了一个同一变量排序下的OBDD合并算法。该算法首先建立目标布尔表达式的表存储模型，然后按照变量排序的逆序，依次处理各个变量，并且合并取值相同的行，直到所有变量处理完毕。

有序决策图（OBDD）；同一变量排序；多有序决策图（OBDD）合并；Apply算法

1 引言

有序二叉决策图（Ordered Binary Decision Diagram，OBDD）是一种用于表示布尔函数的数据结构[1-2]，是迄今为止最为有效的符号技术之一。OBDD已经应用在粗糙集属性约简表示[3]、局部模式挖掘[4]、并行电力系统恢复[5]、网络可靠性分析[6-7]、约束满足问题求解[8-10]等众多领域。

在分布式或者是动态环境下，利用已知布尔函数的OBDD构造目标布尔函数的OBDD是一个关键技术问题。譬如，已知f1、f2和f3的OBDD，构造一个目标表达式f=f1∨(f2∧┐f3)，f的OBDD如何构造？

Colorado大学开发的CUDD软件包[11]，里面包含有Apply操作，即

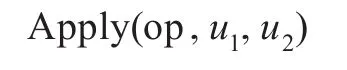
此操作输入表达式u1和u2的OBDD，返回表达式u1op u2的OBDD，其中op是布尔运算符。

一个显而易见的方法是首先构造┐f3的OBDD，然后使用Apply算法求出f2∧┐f3的OBDD，最后再一次使用Apply算法求出的f1∨(f2∧┐f3)的OBDD。显然，上述过程两次使用了Apply算法，且每次使用Apply算法都是基于Shannon分解原理的。

到目前为止，现有的研究均是针对两个表达式的OBDD合成，都没有涉及多个表达式的OBDD合成。例如，古天龙等[12]指出，给定集合S和T，并已知它们的布尔函数，则集合S和T的并、交和差运算等布尔运算都可以由相应的OBDD操作来高效地加以实现。爱丁堡大学的Paul Jackson[13]也对OBDD操作做了总结性的研究，指出可以利用Shannon分解原理以及Apply算法对两个表达式的OBDD进行合成。

鉴于上述分析，本文将在Shannon分解原理的基础上，提出一个同一变量排序下的多OBDD合并算法，用以构造复合布尔表达式的OBDD。

2 OBDD及其存储

OBDD是布尔表达式的一种有效表示方法，它具有规范性，即在给定的变量排序下，任一给定的布尔表达式所对应的OBDD是最简且唯一的。

当绘制OBDD时，0分支用虚线表示，1分支用实线表示，输出值0和1用叶子结点表示。OBDD结构体现了Shannon分解原理，即每一个结点都是一个ite（if-then-else）结构。如果用x→f1，f2表示一个ite(x，f1，f2)结构，则有以下的定义：

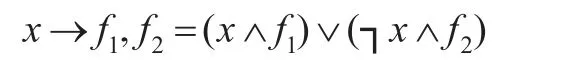
显然，一个ite(x，f1，f2)结构的意义是：若x成立，则选择f1分支；否则，选择f2分支。

在下文中，f[0/x]表示将表达式f中的变量x用0替换，f[1/x]表示将表达式f中的变量x用1替换，显然有：f=x→f[0/x]，f[1/x]，并简写为f=x→f0，f1。

例1有三个布尔表达式f1，f2，f3如下：

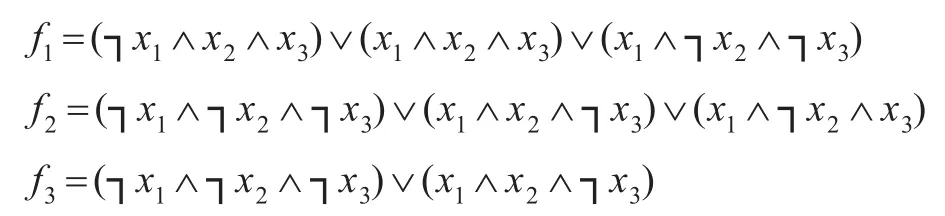
上述三个布尔表达式f1，f2，f3的OBDD如图1（a）（b）（c）。

另外，还可以采用表格的方式来存储一个OBDD，方式如下：每一行存储一个结点的信息；第一列存储是结点的标识；第二列，即表头为var的列，存储的是结点表示的变量；第三列，即表头为0的列，存储的是结点的0分支；第四列，即表头为1的列，存储的是结点的1分支。

对于例1中的三个布尔表达式，对应OBDD的表存储方式见表1（a）（b）（c）。

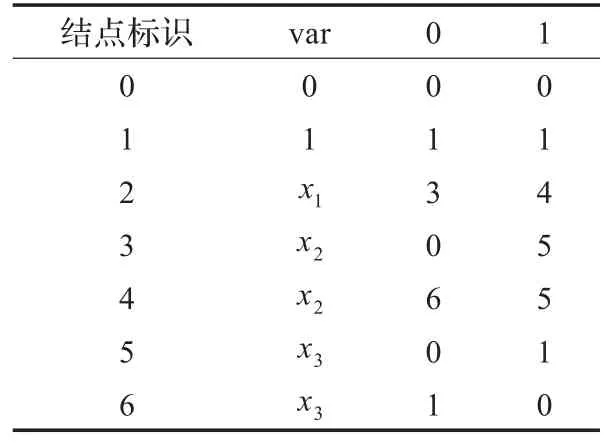
表1 （a）f1的存储表

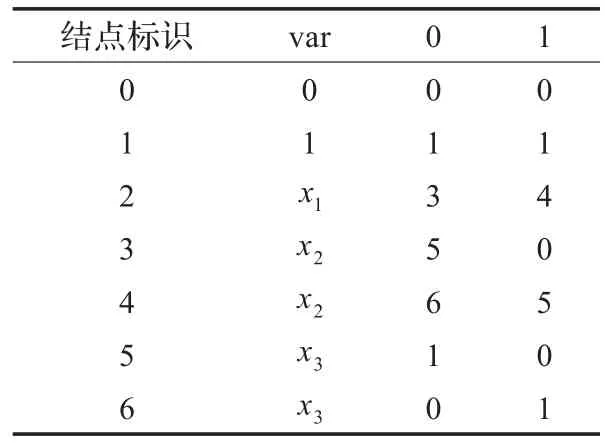
表1 （b）f2的存储表

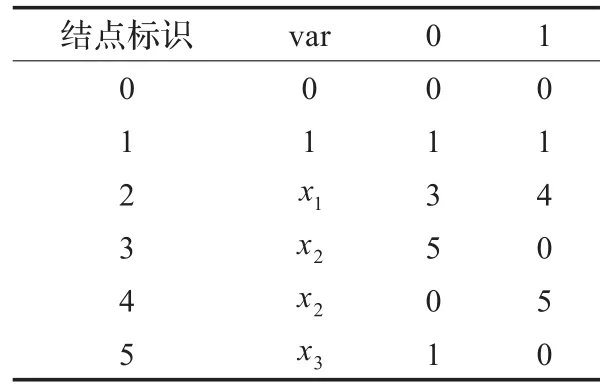
表1 （c）f3的存储表

3 同一变量排序下的多OBDD合并算法

给定义组布尔表达式f1，f2，…，fm，则可以使用逻辑连接符┐，∨，∧，→，↔构造出新的布尔表达式t，即t= F(f1，f2，…，fm)，F表示f1，f2，…，fm的函数。

同一变量排序下的多OBDD合并，即从f1，f2，…，fm的OBDD出发，构造布尔表达式t的OBDD。

算法1同一变量排序下的多OBDD合并算法

输入f1，f2，…，fm的OBDD，布尔表达式t=F(f1，f2，…，fm)

输出布尔表达式t的OBDD

步骤1建立f1，f2，…，fm的OBDD对应的存储表。

图1 （a）布尔表达式f1的OBDD1

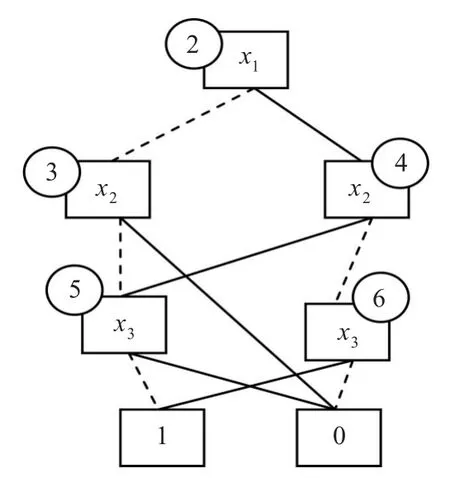
图1 （b）布尔表达式f2的OBDD2

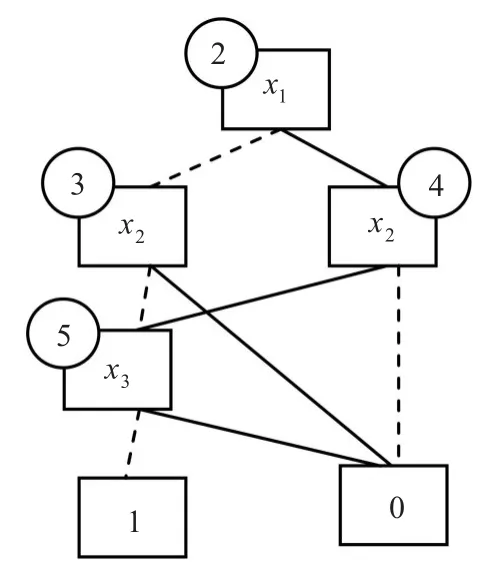
图1 （c）布尔表达式f3的OBDD3

步骤2初始化t的OBDD对应的存储表如表2所示，每一行存储一个结点，并在存储表的右侧增加m列，分别存储该结点在OBDD1，OBDD2，…，OBDDm中的位置。

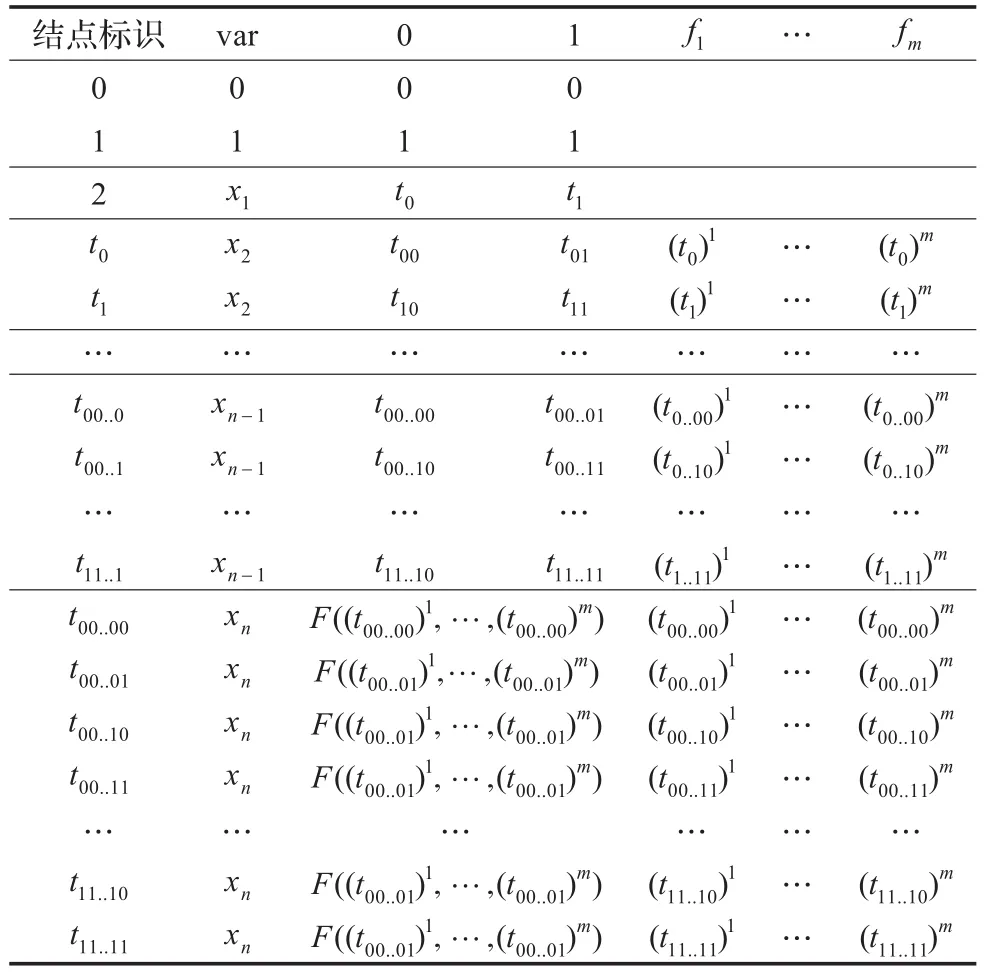
表2 初始存储表

步骤3处理变量xn，使用式子F((t00..00)1，…，(t00..00)m)、F((t00..01)1，…，(t00..01)m)、…、F((t00..01)1，…，(t00..01)m)计算t00..00、t00..01、…、t11..11的值（共2n-1个）。

同时，对于t00..00、t00..01、…、t11..11中的每一个行，若取值为（0，0）或（1，1），则将这一行用0或1代替；若t00..00、t00..01、…、t11..11中存在相同的行，则将这些行用同一标识进行标记。

步骤4设置循环变量i并赋初值n-1，当i＞0时循环执行以下操作：

步骤4-1将变量2i个变量xi+1的值填写到2i-1个变量xi的0分支和1分支当中。

步骤4-2若取值为（0，0）或（1，1），则将这一行用0或1代替。

步骤4-3在标记个变量xi的这2i-1行中，若存在相同的行，则将这些行用同一标识进行标记。

步骤4-4将循环变量i减1，若i＞0，则执行步骤4-1，否则循环结束。

步骤5删除冗余行并对结点进行编号，得到最终的存储表。

步骤6依据存储表建立表达式的OBDD，算法结束。

布尔表达式t=F(f1，f2，…，fm)中变量的数目决定了存储表的规模，存储变量x1，x2，…，xn所占用的空间是一个公比为2的等比数列，因此算法1的空间复杂度为O(2n)。若以处理一行的时间作为衡量算法复杂性的单位时间，那么算法1的时间复杂度为T(2n)。与Apply算法相比，Apply算法一次只能处理一对表达式，而本文的算法能够一次处理任意多个表达式，提高了构造OBDD的效率。

例1（续）f=f1∨(f2∧┐f3)，构造f的OBDD。

步骤1建立f1，f2，f3的OBDD对应的存储表，见表1（a）（b）（c）。

步骤2初始化t的OBDD对应的存储表，如表3所示。

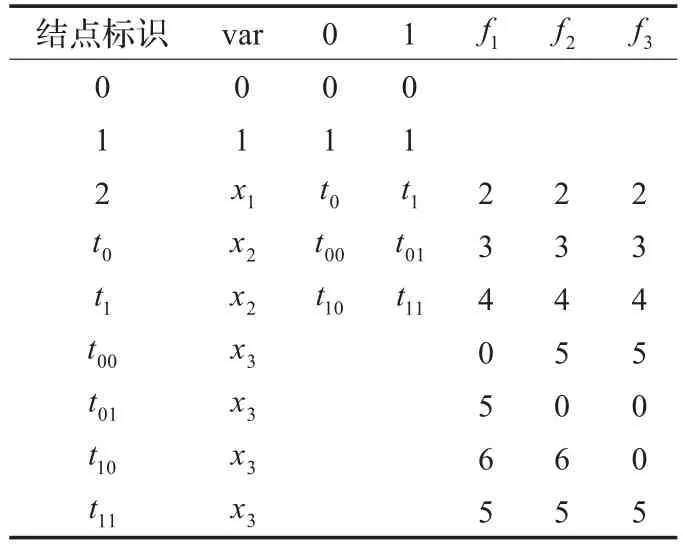
表3 表达式t的初始化存储表

步骤3处理变量x3，计算t00、t01、t10、t11，即

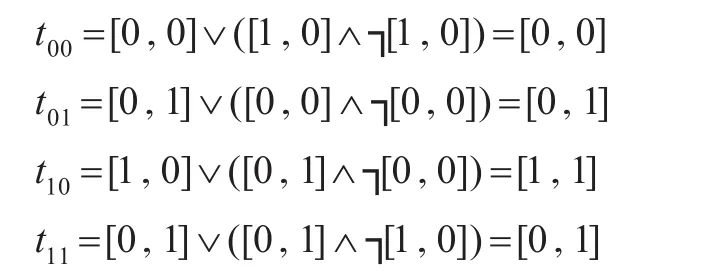
并将t00行的标识修改为0，将t10行的标识修改为1；又因为t01和t11相同，所以将t11的标识修改为t01。

步骤4依次处理变量x2，x1：

对变量x2的处理：对于结点t0，0分支为t00，由于t00的标识已经修改为0，因此t0的0分支修改为0；对于结点t0，0分支为t10，由于t10的标识已经修改为1，因此t0的0分支修改为1。

对变量x1没有修改，最后得到存储表见表4。

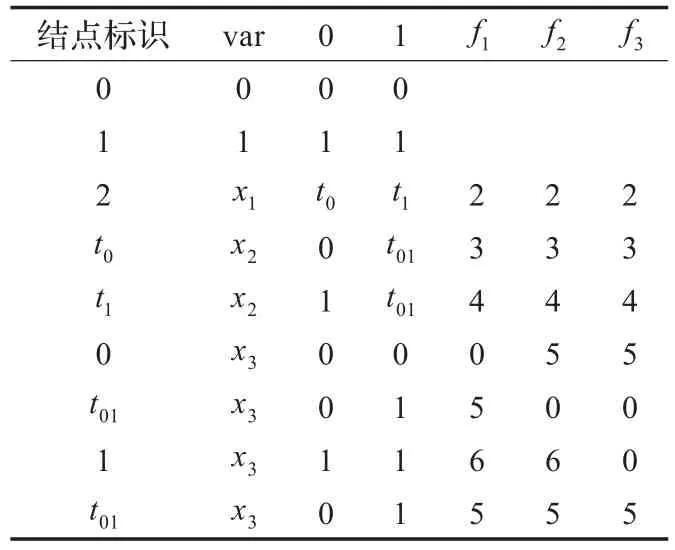
表4 表达式t的存储表

步骤5删除冗余行并对结点进行编号，得到最终的存储表见表5。

步骤6依据存储表建立表达式的OBDD，结果见图2。

表5 重新编号后表达式t的存储表

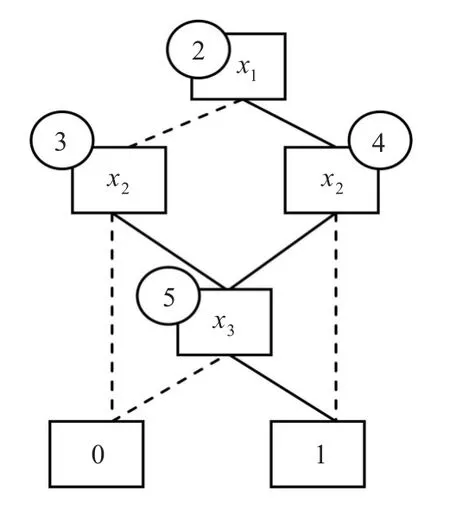
图2 布尔表达式f1∨(f2∧┐f3)的OBDD

4 结束语

在OBDD的应用中，利用已知布尔函数的OBDD构造目标布尔函数的OBDD是一个关键问题。本文利用OBDD的表存储模型，基于Shannon分解原理提出了一个同一变量排序下的OBDD合并算法。与Apply算法相比，Apply算法一次只能处理一对表达式，而本文的算法能够一次处理任意多个表达式，提高了构造OBDD的效率。

[1]Akers S B.Binary decision diagrams[J].IEEE Transactions on Computer，1978，27（6）：509-516.

[2]Bryant R E.Graph based algorithms for Boolean function manipulation[J].IEEE Transactions on Computer，1986，35（8）：677-691.

[3]Wei Qianjin，Gu Tianlong.Symbolic representation for rough set attribute reduction using ordered binary decision diagrams[J].Journal of Software，2011，6（6）：977-984.

[4]Yang Liu，M anadhata P K，Horne W G，et al.Fast submatch extraction using OBDDs[R].[S.l.]：HP Laboratories，2012.

[5]Wang Chong，Vittal V，Sun K.OBDD-based sectionalizing strategies for parallel power system restoration[J].IEEE Transactions on Power System s，2011，26（3）：1426-1433.

[6]陈瑶，李峭，赵长啸，等.基于OBDD的航空电子网络可靠性分析[J].系统工程与电子技术，2013，35（1）：230-236.

[7]赵勃，肖宇峰，刘岩.基于OBDD的通信网链路重要性评估[J].系统工程与电子技术，2011，33（10）：2348-2352.

[8]徐周波，古天龙，常亮，等.约束满足问题求解的符号OBDD桶消元算法[J].计算机科学，2011，38（7）：200-203.

[9]徐周波，古天龙.装配序列规划问题的CSP模型及其符号OBDD求解技术[J].计算机辅助设计与图形学学报，2010，22（5）：803-810.

[10]古天龙，杨志飞.基于有序二叉决策图的装配序列符号表示方法[J].计算机辅助设计与图形学学报，2007，19（10）：1315-1320.

[11]Somenzi F.CUDD：CU decision diagram package release 2.4.1[EB/OL].[2013-09-11].http：//vlsi.Colorado.edu/fabio/ CUDD/cudd Intro.htm l.

[12]古天龙，吕思菁，常亮，等.基于OBDD的描述逻辑εL循环术语集推理[J].软件学报，2014，25（1）：64-77.

[13]Jackson P.BDD operations[EB/OL].[2013-12-21].www.inf. ed.ac.uk/teaching/courses/ar/slides/bdd-ops.pdf.

ZHI Huilai

School of Computer Science and Technology, Henan Polytechnic University, Jiaozuo, Henan 454000, China

Ordered Binary Decision Diagrams（OBDD）is a Boolean function representation data structure, and has been applied in many fields. In dynamic or distribute environment, how to efficiently build OBDD of the target Boolean expression form the known Boolean expression’s OBDD is a frequent encountered problem. Under identical variable ordering,this paper puts forward a OBDD merging algorithm based on Shannon decomposition principle. In the algorithm, it firstly establishes a storage table for the target Boolean expression, and then under the reverse variable ordering it handles each variable in turn, and combines the rows with same values, until all the variables are handled.

words：Ordered Binary Decision Diagrams（OBDD）; identical variable ordering; multiple Ordered Binary Decision Diagrams（OBDD）merging; Apply algorithm

ZHI Huilai. Multiple OBDD merging algorithm under same variable ordering. Computer Engineering and Applications,2014, 50（17）：20-23.

A

TP18

10.3778/j.issn.1002-8331.1312-0067

国家自然科学基金（No.60975033）；河南理工大学博士基金（No.B2011-102）。

智慧来（1981—），男，博士，讲师，研究领域包括形式概念分析、知识表示与推理等。E-mail：zhihuilai@126.com

2013-12-05

2014-03-10

1002-8331（2014）17-0020-04

CNKI网络优先出版：2014-03-19,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1312-0067.htm l