Bézier曲线到AH-Bézier曲线的升阶算法

沈莞蔷，汪国昭

1.江南大学理学院，江苏无锡 214122

2.浙江大学CAD&CG国家重点实验室，杭州 310027

3.浙江大学数学系，杭州 310027

Bézier曲线到AH-Bézier曲线的升阶算法

沈莞蔷1，汪国昭2，3

1.江南大学理学院，江苏无锡 214122

2.浙江大学CAD&CG国家重点实验室，杭州 310027

3.浙江大学数学系，杭州 310027

关于曲线升阶，已有的结论往往限于同类曲线之间。为了突破这一限制，考虑不同类曲线间的升阶，关注代数多项式空间中的Bézier曲线到代数双曲多项式空间中的AH-Bézier曲线的升阶。研究从基函数入手，利用Bézier和AH-Bézier共有的求导降阶的特点，结合矩阵分块的思想，先给出AH-Bézier基到Bernstein基的转换矩阵，进而推出控制顶点的升阶公式，最后给出升阶算法。结果表明，任意n次Bézier曲线可以通过该算法升到n+3阶（等同于n+2次）的AH-Bézier曲线。算法实现了Bézier到AH-Bézier曲线模型的精确转换。

Bézier曲线；AH-Bézier曲线；升阶；基函数；转换矩阵

1 引言

在计算机辅助几何设计中，Bézier是最简单，最常用的模型之一。它在代数多项式空间中定义，可造型曲线的种类不够多，不能精确表示圆、双曲线等经典曲线。有理Bézier造型丰富，但有求高阶导复杂和分母零点的奇异性等特点。因此，近年来，可用非有理形式造型圆等经典曲线的其他空间的拟Bézier系统不断涌现[1]。譬如，纯三角空间的p-Bézier[2]和T-Bézier[3]，纯双曲空间的拟Bézier[4]，代数三角混合空间的C-Bézier[5-6]，代数双曲混合空间的AH-Bézier[7]，代数三角双曲混合空间的AHT Bézier[8]，以及用复数思想统一代数三角双曲的ω-Bézier[9-10]等。这些拟Bézier系统得到了广泛深入的研究，已应用于数据压缩[11]、工程曲线曲面的造型[12]与设计[13]等方面。

升阶是现有曲线造型系统的常用手段。它可以增加曲线的自由度，用于组合曲线的设计和表示等方面[14]。现有的升阶，往往考虑同类曲线之间由低次升到高次，如Bézier曲线的升阶[15]，纯双曲拟Bézier曲线的升阶[4]，C-Bézier曲线的升阶[16]等。即使对于混合曲线，如C-Bézier，也仅是针对其中同类的代数多项式的次数进行提升，即从空间span{1，sin t，cos t，t，t2，…，tn}升到空间span{1，sin t，cos t，t，t2，…，tn，tn+1}。

本文将考虑不同类曲线间的升阶。从代数多项式空间，提升双曲多项式部分的阶数，从而得到代数双曲混合空间。换句话说，将空间S1=span{1，t，t2，…，tn}升2阶到空间S2=span{1，sh t，ch t，t，t2，…，tn}。相应的，S1中的n次Bézier曲线升阶到S2中的n+3阶（等同于n+2次）的AH-Bézier曲线。

因为空间S1⊂S2，所以，升阶公式必定存在。它关键在于AH-Bézier基到Bernstein基的转换矩阵。由于基表示的唯一性，该矩阵必定唯一。混合空间中的拟Bézier基和拟B样条基的转换矩阵已经给出[17]，但混合拟Bézier基转换到Bernstein基的矩阵还未有研究。本文就考虑这个转换矩阵，从而给出曲线的升阶公式，再给出升阶算法。

定义在空间S2上的n+3阶AH-Bézier曲线[7]，其基函数{Hi，n+2:=Hi，n+2(t)，i=0，1，…，n+2}可采用如下方法给出。

其中，Qi，0≤i≤n+2为控制顶点。

由于AH-Bézier的参数t∈[0，α]，因此，考虑同样参数区间的n次Bézier曲线：

为n次Bernstein基函数，参数t∈[] 0，α。

本文研究n次Bézier曲线（5）升2阶到n+3阶（n+2次）的AH-Bézier曲线（4）的算法。

2 Bézier到AH-Bézier的升阶公式

本章研究升阶公式，先考虑n+3阶（n+2次）AHBézier基到n次Bernstein基的转换矩阵，再推出曲线的升阶公式。

2.1 基函数的转换矩阵

总结本节的内容，可得如下定理。

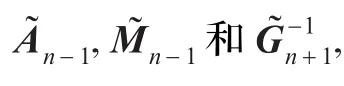
2.2 曲线的升阶公式

根据上节的升阶公式，得到曲线的升阶公式，表述为如下定理。

定理2（Bézier曲线到AH-Bézier曲线的升阶）对任意n≥0，n次Bézier曲线（5）可升阶到n+3阶（n+2次）AH-Bézier曲线（4），其控制顶点的关系为：

其中，Mn为(n+1)×(n+3)阶矩阵，初始值M0由式（17）给出，递推关系由式（16）给出。

3 Bézier到AH-Bézier的升阶算法

根据上章给出的升阶公式，本章先给出升阶算法，再给出例子。

3.1 升阶算法

算法1（Bézier曲线到AH-Bézier曲线的升阶）给定n次Bézier曲线的控制顶点(P0P1…Pn)，以及任意常数α＞0，则该Bézier曲线可升2阶到以α为形状参数的n+3阶（n+2次）AH-Bézier曲线，升阶后的控制顶点(Q0Q1…Qn+2)可通过如下算法得到。

3.2 情况n=1

当n=1时，升阶前的Bézier曲线为直线。此时，升阶公式为：对于矩阵C1和D1的每一列，仅有一个或两个相邻元素非零，且非零元素和为1。这表示在某条控制边上取点，即为割角形式。在这n=1的升阶过程中，C1和D1各代表一次割角，总共有两次割角。

在本文的所有例子中，升阶前的控制顶点，控制多边形和Bézier曲线分别用蓝色空心圈，蓝色实折线和蓝色粗实曲线表示；升阶后的控制顶点，控制多边形和AH-Bézier曲线分别用红色星号，红色虚折线和红色细实曲线表示。在这些例子中，蓝色曲线和红色曲线完全重合。由于蓝色曲线比红色曲线粗，因此，蓝曲线的中间部分被红曲线覆盖，仅边界部分可见。两曲线重合，是由于升阶前后的曲线并不改变，同时验证了本文升阶公式及算法的正确性。

图1给出n=1的例子。α=1。初始Bézier曲线（直线）的两个控制顶点用蓝色空心圈表示。在升阶过程中，第一次割角的三个控制顶点用绿色菱形表示，第二次割角的四个控制顶点即为升阶后AH-Bézier曲线的控制顶点。它们用红色星号表示。

图1 n=1的例子

3.3 情况n=2

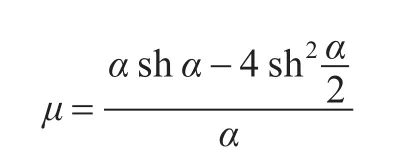
将M2分解成两个矩阵的乘积：

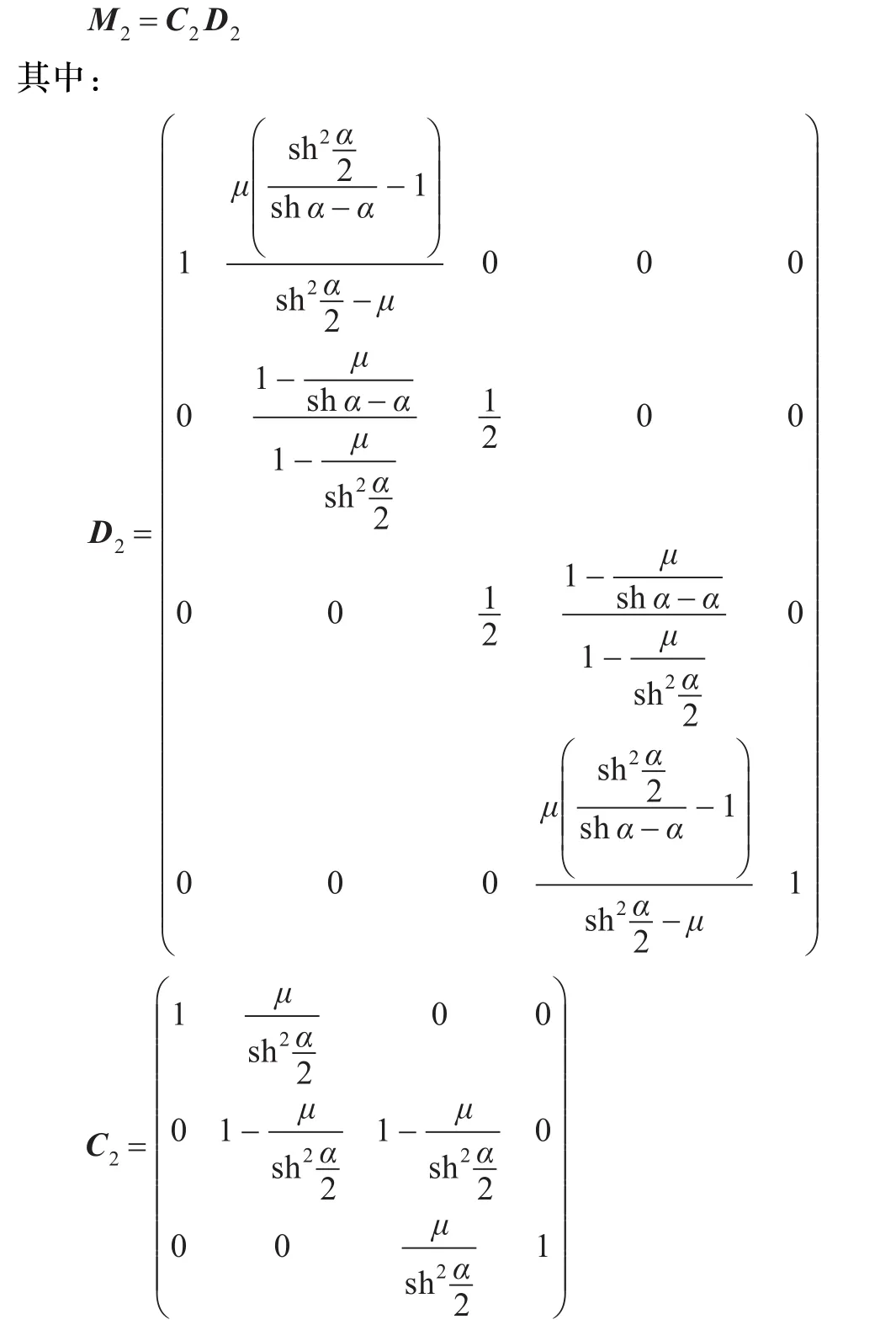
与n=1的情况类似，C2和D2各代表一次割角。因此，这n=2的升阶过程，也可以表示为两次割角。

图2给出n=2的例子。α=1。初始Bézier曲线的三个控制顶点用蓝色空心圈表示，控制多边形用蓝色实线表示。在升阶过程中，第一次割角的四个控制顶点用绿色菱形表示，它们依次连接而成的控制多边形用绿色点划线表示，第二次割角的五个控制顶点即为升阶后AH-Bézier曲线的控制顶点。它们用红色星号表示，之间用红色虚线连接。

图2 n=2的例子

3.4 关于形状参数

形状参数α会影响升阶后的AH-Bézier曲线的控制顶点。

图3给出同一条Bézier曲线升阶到带有不同形状参数α的AH-Bézier曲线的例子。其中，子图（a），（b），（c）中的α分别取1，5，10。从中可以看出，尽管升阶前Bézier曲线的控制顶点都相同，但是由于α不同，升阶后的AH-Bézier曲线的控制顶点不全相同。

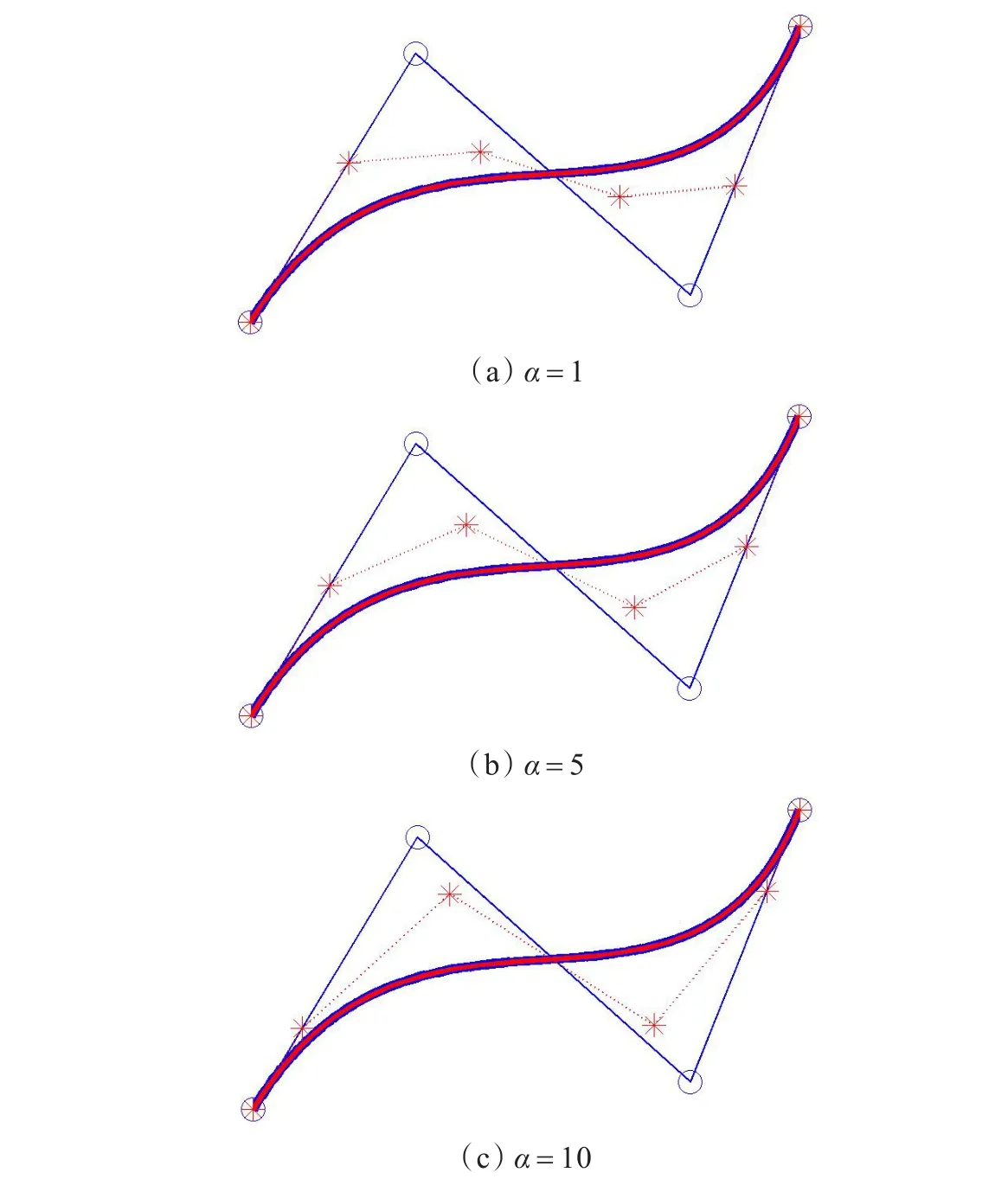
图3 不同形状参数的升阶例子

4 结束语

本文给出了任意n次Bézier曲线到n+3阶（n+2次）AH-Bézier曲线的升阶算法。通过该算法，任意n次的Bézier曲线都可以精确表示为高2阶的AH-Bézier曲线。将来的工作要进一步考虑算法的几何意义，希望将任意次的升阶算法表示成割角形式，并且将类似工作推广到其他混合形式的拟Bézier曲线中。

[1]Mainar E，Peňa J M.A general class of Bernstein-like bases[J].Computers & Mathematics with Applications，2007，53（11）：1686-1703.

[2]Sánchez-Reyes J.Harmonic rational Bézier curves，p-Bézier curves and trigonometric polynomials[J].Computer Aided Geometric Design，1998，15（9）：909-923.

[3]严兰兰，韩旭里，邬国根，等.二/三阶三角Bézier曲线[J].图学学报，2013，34（5）：71-75.

[4]Shen W Q，Wang G Z.A class of quasi Bézier curves based on hyperbolic polynomials[J].Journal of Zhejiang University：Science A，2005，6（SUPPL.I）：116-123.

[5]Zhang J W.C-curves：an extension of cubic curves[J].Computer Aided Geometric Design，1996，13（3）：199-217.

[6]Chen Q Y，Wang G Z.A class of Bézier-like curves[J].Computer Aided Geometric Design，2003，20（1）：29-39.

[7]Li Y J，Wang G Z.Two kinds of B-basis of the algebraic hyperbolic space[J].Journal of Zhejiang University：Science A，2005，6（7）：750-759.

[8]Xu G，Wang G Z.AHT Bézier curves and NUAHT B-spline curves[J].Journal of Computer Science and Technology，2007，22（4）：597-607.

[9]Zhang J W，Krause F L，Zhang H Y.Unifying C-curves and H-curves by extending the calculation to complex numbers[J].Computer Aided Geometric Design，2005，22（9）：865-883.

[10]Fang M E，Wang G Z.ω-Bézier[C]//10th IEEE International Conference on Computer Aided Design and Computer Graphics，Beijing，China，2007：38-42.

[11]秦新强，王伟伟，胡钢.基于遗传算法的C-Bézier曲线降阶[J].计算机工程与应用，2013，49（5）：174-178.

[12]师利红，张贵仓.三次TC-Bézier曲线的新扩展[J].计算机工程与应用，2011，47（4）：201-204.

[13]蔡华辉，王国瑾.三次C-Bézier螺线的构造及其在道路设计中的应用[J].浙江大学学报工学版，2010，44（1）：68-74.

[14]朱平，汪国昭.B-样条曲线升阶的几何收敛性[J].工程图学学报，2010，44（1）：100-103.

[15]王国瑾，汪国昭，郑建民.计算机辅助几何设计[M].北京：高等教育出版社，2001：35-43.

[16]单开佳，汪国昭.低阶C-Bézier曲线的升阶[J].高校应用数学学报A辑，2002，17（4）：441-445.

[17]Wang G Z，Li Y J.Optimal properties of the uniform algebraic trigonometric B-splines[J].Computer Aided Geometric Design，2006，23（2）：226-238.

SHEN Wanqiang1,WANG Guozhao2，3

1.School of Science, Jiangnan University, Wuxi, Jiangsu 214122, China
2.State Key Lab of CAD & CG, Zhejiang University, Hangzhou 310027, China
3.Department of Mathematics, Zhejiang University, Hangzhou 310027, China

The existing results about curve degree elevation are mainly limited to the same type of curves. In order to push the limit and consider degree elevation between different types of curves, this paper focuses on degree elevation algorithm from Bézier curve, defined on algebraic polynomial space, to AH-Bézier curve, defined on algebraic and hyperbolic polynomial space. The study begins with basis functions. Firstly, the transformation matrix from AH-Bézier basis to Bernstein basis is built by using the block matrix idea and the same property of Bézier and AH-Bézier that the order of basis is reduced for derivative. Secondly, the degree elevation formula of control points is obtained. Lastly, the degree elevation algorithm is given. Results show that any Bézier curve of degree n can be turned into an AH-Bézier curve of order n+3（i.e.degree n+2）by using this algorithm. The algorithm gives an accurate transformation from Bézier to AH-Bézier curve model.

Bézier curve; AH-Bézier curve; degree elevation; basis function; transformation matrix

SHEN Wanqiang, WANG Guozhao. Degree elevation algorithm from Bézier curve to AH-Bézier curve. Computer Engineering and Applications, 2014, 50（17）：7-11.

A

TP391.7

10.3778/j.issn.1002-8331.1403-0209

国家自然科学基金专项数学天元基金项目（No.11326243）；国家自然科学基金面上项目（No.61272300，No.11371174）；江苏省自然科学基金青年基金项目（No.BK 20130117）。

沈莞蔷（1981—），女，博士，讲师，研究领域为计算机辅助几何设计、计算机图形学；汪国昭（1944—），男，教授，博导，研究领域为计算机辅助几何设计、计算机图形学、医学图像处理。E-mail：wq_shen@163.com

2014-03-17

2014-05-16

1002-8331（2014）17-0007-05

CNKI网络优先出版：2014-06-26,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1403-0209.htm l