区间值强模糊图的运算性质

索南仁欠，李生刚

1.陕西师范大学数学与信息科学学院，西安 710062

2.青海师范大学数学系，西宁 810008

区间值强模糊图的运算性质

索南仁欠1，2，李生刚1

1.陕西师范大学数学与信息科学学院，西安 710062

2.青海师范大学数学系，西宁 810008

利用经典图和模糊图定义和性质，给出了区间值模糊关系、模糊变换以及区间值强模糊图的定义，相应地定义了区间值强模糊图弱直积、半直积运算，并且证明了其弱直积、半直积运算封闭的性质。

模糊图；区间值；区间值强模糊图；弱直积；半直积

在Rosenfeid提出了若干模糊图的相关概念及性质后，初步建立了模糊图论系统。之后，Bhattacharya[1]、Peng[2]、Sunitha以及Kumar[3]以经典图之间的运算为基础，定义了模糊图的补并研究了补的其他性质及运算；在文献[4-7]中系统描述了模糊图中最优路、强树的连通性及边的特点；文献[8-9]中又提出了完全模糊图和正则模糊图，进一步改进和发展了模糊图理论，使得模糊图论体系不断完善。

作为模糊集的一类推广，1975年，Zadeh[10]又提出了区间值模糊集的概念。近年来，国外许多学者相继补充研究了区间值模糊图的更多相关性质。M.Akram在文献[11-12]中给出了一些区间值模糊图的确定类型并引进了线图定义及其性质；A.A.Talebi在文献[13]中讨论了自补和自弱补区间值模糊图及其相关的运算；H. Rashmanlou在文献[14]中给出了完全区间值模糊图的一些相关运算。同时，国内也有研究人员给出了许多区间值模糊图的相关理论。近期，杨文华和李生刚[15-16]就区间值模糊图的运算性质给出了补充研究。

1 预备知识

定义1.1[17]（模糊图）一个模糊图G′是一个有序三元组G′=(G，σ，μ)，其中G=(V(G)，E(G)，φG)是一个（无向，有限）经典图，称为基图，σ:V(G)→(0，1]，μ:E(G)→(0，1]，且∀e∈E(G)，μ(e)≤σ(μ)∧σ(υ)，这里μ，υ是e的端点。

若基图G=(V(G)，E(G)，φG)是一个有限图，则模糊图G′=(G，σ，μ)也是一个有限图。若基图G=(V(G)，E(G)，φG)是一个完全图，则模糊图G′=(G，σ，μ)也是一个完全图。若基图G=(V(G)，E(G)，φG)是一个连通图，则模糊图G′=(G，σ，μ)也是一个连通图。

2 区间值模糊图的简单运算

定义2.1（区间值模糊关系）基于图G=(V，E)，设B为V上的区间值模糊关系，B=[，]为B的隶属函数。若ek=vivj，则记μB(ek)=μB(vivj)。此关系满足以下性质：

①μB(vivj)=μB(vjvi)（对称性）；

②对于任意的i，μB(vivi)=0，即(vi)=(vi)=0（反自反性）。

μB(vivj)即为vi，vj之间的区间连接程度。

定义2.2（区间值模糊变换）设X和Y均为论域，任意的区间值模糊关系B都唯一地确定了一个X到Y的区间值模糊变换TB，对于任意区间值模糊集合A满足：

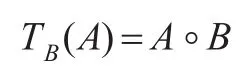
其隶属函数为：

定义2.3（弱直积）设G1=(A1，B1)是=(V1，E1)的区间值模糊图和G2=(A2，B2)是=(V2，E2)的区间值模糊图，且V1∩V2=φ。在图G*=(V1×V2，E)上的弱直积被定义为：

定义2.4（半直积）设G1=(A1，B1)是=(V1，E1)的区间值模糊图和G2=(A2，B2)是=(V2，E2)的区间值模糊图，且V1∩V2=φ。在图G*=(V1×V2，E)上的半直积被定义为：

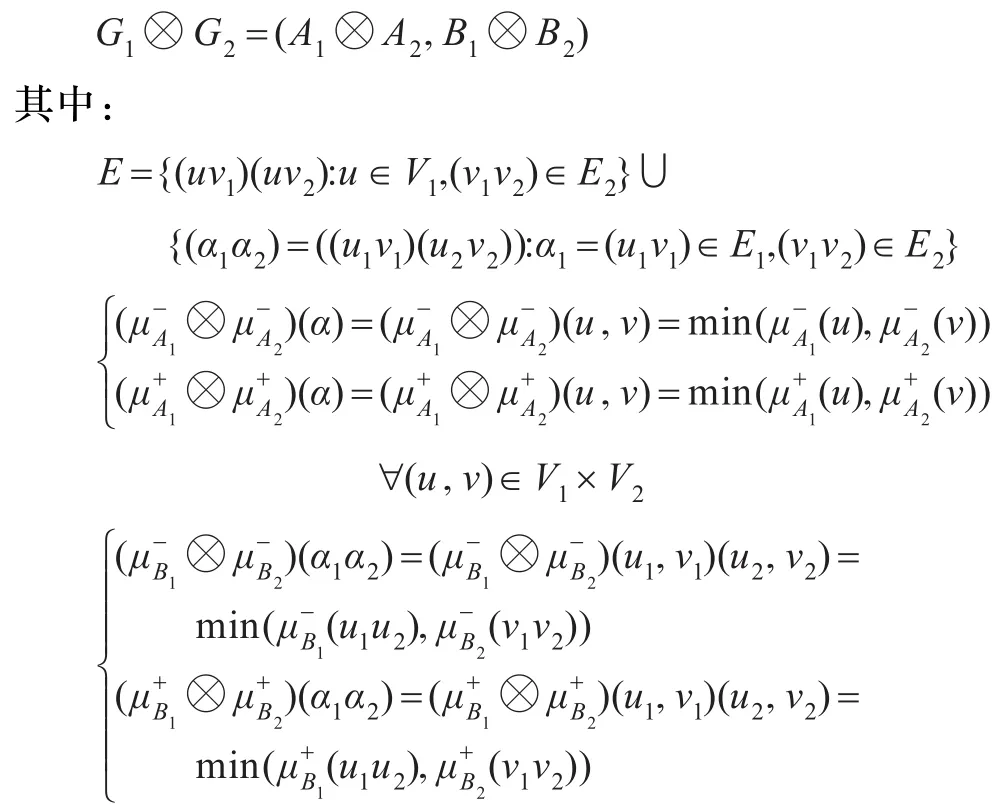
以上两个条件，即满足定义2.1的条件，再给出以下条件：

定义2.5（直积）设G1=(A1，B1)是=(V1，E1)的区间值模糊图和G2=(A2，B2)是=(V2，E2)的区间值模糊图，且V1∩V2=φ。在图G*=(V1×V2，E)上的直积被定义为：

以上两个条件满足定义2.1的条件：

以上三个条件满足定义2.2的条件，再给出以下条件：

3 区间值模糊图的运算性质

命题3.1设G1=(A1，B1)是=(V1，E1)的区间值强模糊图和G2=(A2，B2)是G2*=(V2，E2)的区间值强模糊图，且V1∩V2=φ。则G1*G2=(A1*A2，B1*B2)也是区间值强模糊图。

证明设G1=(A1，B1)是=(V1，E1)的区间值强模糊图和G2=(A2，B2)是=(V2，E2)的区间值强模糊图，且V1∩V2=φ。又α1α2=(u1v1)(u2v2)∈E，有：

则G1*G2=(A1*A2，B1*B2)也是区间值强模糊图。如图1所示。

图1 区间值强模糊图的弱直积

推论3.1若G1*G2=(A1*A2，B1*B2)是区间值强模糊图，则G1=(A1，B1)或G2=(A2，B2)是区间值强模糊图。

命题3.2设G1=(A1，B1)是=(V1，E1)的区间值强模糊图和G2=(A2，B2)是=(V2，E2)的区间值强模糊图，且V1∩V2=φ，则G1⊗G2=(A1⊗A2，B1⊗B2)也是区间值强模糊图。

证明设G1=(A1，B1)是G1*=(V1，E1)的区间值强模糊图和G2=(A2，B2)是G2*=(V2，E2)的区间值强模糊图，且V1∩V2=φ。又(u，v1)(u，v2)∈E，有：

由命题3.1知，G1⊗G2=(A1⊗A2，B1⊗B2)也是区间值强模糊图。例如图2所示。

图2 区间值强模糊图的半直积

推论3.2若G1⊗G2=(A1⊗A2，B1⊗B2)是区间值强模糊图，则G1=(A1，B1)或G2=(A2，B2)是区间值强模糊图。

命题3.3设G1=(A1，B1)是G1*=(V1，E1)的区间值强模糊图和G2=(A2，B2)是G2*=(V2，E2)的区间值强模糊图，且V1∩V2=φ。则G1#G2=(A1#A2，B1#B2)也是区间值强模糊图。

证明设G1=(A1，B1)是G1*=(V1，E1)的区间值强模糊图和G2=(A2，B2)是G2*=(V2，E2)的区间值强模糊图，且V1∩V2=φ。有：

由命题3.2知G1#G2=(A1#A2，B1#B2)也是区间值强模糊图。如图3所示。

图3 区间值强模糊图的直积

推论3.3若G1#G2=(A1#A2，B1#B2)是区间值强模糊图，则G1=(A1，B1)或G2=(A2，B2)是区间值强模糊图。

4 结语

在模糊图论中，有直观模糊图的相关性质，对于区间值模糊图可否找到直观的区间值模糊图，能否建立模型，使已研究的区间值模糊图的理论应用到相关的领域，这些都是下一步有待解决的问题。

从目前的发展趋势看来，模糊图论已在聚类分析、数据理论、Network分析以及信息理论等方面体现出重要的应用价值，关于模糊图论的研究也受到了众多学者的关注。模糊图论必然会像经典图论一样，发展成为更系统、结构性更紧密的理论研究基础。

[1]Bhattacharya P.Some remarks on fuzzy graphs[J].Pattern Recognition Letters，1987，6：297-302.

[2]Mordeson J N，Peng C S.Operations on fuzzy graphs[J].Information Sciences，1994，79：159-170.

[3]Sunitha M S，Vijaya Kumar A.Complement of a fuzzy graph[J].Indian J Pure Appl Math，2002，33（9）：1452-1464.

[4]彭祖赠，孙韫玉.模糊（Fuzzy）数学及其应用[M].2版.武汉：武汉大学出版社，2004：115-146.

[5]Bhutani K R，Rosenfeld A.Strong arcs in fuzzy graphs[J].Information Sciences，2003，152：319-322.

[6]Mathew S，Sunitha M S.Types of arcs in fuzzy graph[J].Information Sciences，2009，179：1760-1768.

[7]Bhutani K R，Battou A.On M-strong fuzzy graphs[J]. Information Sciences，2003，155：103-109.

[8]Al-Hawary T.Complete fuzzy graphs[J].International J Math Combin，2011，4：26-34.

[9]Nagoor Gani A，Kadha K.On regular fuzzy graphs[J].J Physical Sciences，2008，12：33-40.

[10]Zadeh L A.The concept of a linguistic and application to approximate reasoning I[J].Information Sciences，1975，8：199-249.

[11]Akram M，Alshehri N O，Dudek W A.Certain types of interval-valued fuzzy graphs[J].Journal of Applied Mathematics，2013，7：1-11.

[12]Akram M.Interal-valued fuzzy line graphs[J].Neural Computing Applications，2012，21：145-150.

[13]Talebi A A，Rashmanlou H.Isomorphism on interval-valued fuzzy graphs[J].Annals of Fuzzy Mathematics and Informatics，2012，4：1-11.

[14]Rashmanlou H，Jun Y B.Complete interval-valued fuzzy graphs[J].Annals of Fuzzy Mathematics and Informatics，2010，23：31-42.

[15]杨文华，李生刚.区间值模糊图的运算性质[J].模糊系统与数学，2013（2）：127-135.

[16]杨文华，李生刚.区间值模糊图的分解性质[J].计算机工程与应用，2012，48（31）：25-29.

[17]Akram M，Dudek W A.Interval-valued fuzzy graphs[J].Computers and Mathematics with Applications，2011，61（2）：289-299.

SUONAN Renqian1，2,LI Shenggang1

1.College of Mathematics and Information Science, Shaanxi Normal University, Xi’an 710062, China
2.Department of Mathematics, Qinghai Normal University, Xining 810008, China

Using the classical graph and fuzzy graph definition and nature, it gives the definition of fuzzy relation, fuzzy interval value and interval valued fuzzy graph transformation, the corresponding definition of interval valued fuzzy graph weak direct product, semi direct product operation, and proves the weak direct product, semi direct product property operation closed.

fuzzy graph; interval value; strong interval value fuzzy graph; weak direct product; semidirect product

SUONAN Renqian, LI Shenggang. Strong interval value fuzzy operation properties of graph. Computer Engineering and Applications, 2014, 50（17）：12-15.

A

O159

10.3778/j.issn.1002-8331.1403-0112

国家自然科学基金（No.11061026，No.11071151）。

索南仁欠（1969—），男，教授，研究方向：代数图论、代数组合论。E-mail：1317087364@qq.com

2014-03-12

2014-05-13

1002-8331（2014）17-0012-04