双极值模糊软子群和双极值模糊正规软子群

殷霞，廖祖华，章里程，朱晓英

江南大学理学院，江苏无锡 214122

双极值模糊软子群和双极值模糊正规软子群

殷霞，廖祖华，章里程，朱晓英

江南大学理学院，江苏无锡 214122

研究了双极值模糊软子群的等价刻画。在双极值模糊软子群的基础上定义了双极值模糊正规软子群，得到了它的一些性质及等价刻画，进一步还研究了在双极值模糊软同态下，双极值模糊正规软子群的像与原像一些性质。

双极值模糊软集；双极值模糊软子群；双极值模糊正规软子群；双极值模糊软同态

1 引言

1999年，俄罗斯学者M olodtsov[1]提出了软集的概念，软集是一种全新的处理不确定性、不精确性问题的数学工具。2003年，M aji[2]等给出了软集的运算及它们的基本性质。此后，基于这些运算，软集被广泛应用到数学、信息科学、计算科学等各个学科领域，并取得了很大的成就[3-8]。

给定一个初始论域X和一个参数集A，X上软集就是从参数集A到X的幂集的一个集值函数。但是一般的集合没有代数结构，为了丰富软集理论，建立软集的代数结构，2007年Aktaş和Çağman[9]在研究软集理论的基础上，首次把软集理论应用到群论中，提出了软群的概念：设G是一个群，(F，A)是群G上的软集，称软集(F，A)是群G上的软群当且仅当∀ ε∈A，F(ε)是G的子群。在此基础上，Aktaş和Çağman研究并讨论了软群的一些基本性质，初步建立了软群理论。之后，许多学者将这一定义的方式拓展到其他的代数系统上，深入研究了软集的代数性质[10-16]，这些研究工作对代数学的发展起到了极大的推动作用。

1994年，Zhang[17]给出了模糊集的一种推广即双极值模糊集。随着研究的不断深入，杨文华[18]等将软集与双极值模糊集相结合提出了双极值模糊软集的概念，研究了它们的运算及性质，这使软集理论进一步得到了充实。利用这一概念，殷霞[19]等将双极值模糊软集应用到群论中，提出了双极值模糊（反）软子群的概念并研究了它们的基本性质。本文在前面工作的基础上，进一步研究了双极值模糊软子群的等价刻画，提出了双极值模糊正规软子群的概念，并讨论了它的代数性质。

2 预备知识

本章给出双极值模糊集、模糊软集、双极值模糊软集等基本概念，同时定义群上双极值模糊软集的一些运算并给出其基本性质。

定义2.1[17]设X是一个初始论域，μP:X→[0， 1]，μN:X→[-1， 0]是两个映射，则称B={(x，μP(x)，μN(x))| x∈X}是X上的一个双极值模糊集，简记为B= (，μ)。这里，正隶属度μ(x)表示元素x关于双极值模糊集B对某性质的满足度，负隶属度μ(x)表示元素x关于双极值模糊集B对这种性质的相反性质的满足度。

设X是一个初始论域，X上的所有双极值模糊集的全体记为BFX。

定义2.2[3]设X是一个论域，E是参数集，A⊆E，X上的一个模糊软集是指序对(F，A)，其中F:A→IX( I=[0，1])是一个映射，即∀ ε∈A，F(ε):X→I是X上的模糊集合。

定义2.3[18]设X是一个论域，E是参数集，A⊆E，X上的一个双极值模糊软集是指一个序对(F，A)，其中F:A→BFX是一个映射。

换句话说，一个X上双极值模糊软集就是X上的一些双极值模糊集构成的参数族。即∀ ε∈A，F(ε)是一个与ε相关的X上的双极值模糊集

定义2.4[18]设X是一个论域，E是参数集，A，B⊆E，(F，A)和(K，B)是X上的两个双极值模糊软集，若(F，A)和(K，B)满足下列两个条件：

（1）A⊆B。

（2）∀ ε∈A，F(ε)是K(ε)的双极值模糊子集，即是(K，B)的双极值模糊软子集，记为(F，A)(K，B)。

定义2.5[18]设(F，A)和(K，B)是X上的两个双极值模糊软集，若(F，A)K，B)且(K，B)(F，A)，则称(F，A)和(K，B)是双极值模糊软相等的。

下面取初始论域X为群G，定义群上双极值模糊软集的乘积与逆运算，并给出这两种运算的基本性质。

定义2.6设(F，A)和(K，B)是群G上的两个双极值模糊软集，称双极值模糊软集(H，C)是(F，A)与(K，B)的乘积，记作(H，C)=(F，A)(K，B)，如果C= A∩B，且∀ε∈C，∀z∈G有：

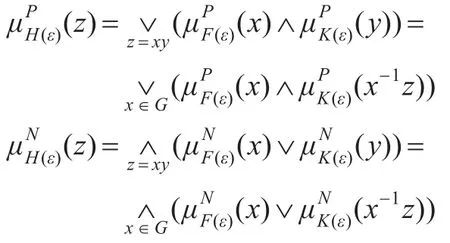
定义2.7设(F，A)是群G上的双极值模糊软集，称双极值模糊软集(F-1，A)是(F，A)的逆，记作(F，A)-1= (F-1，A)，如果∀ε∈A，∀x∈G有：

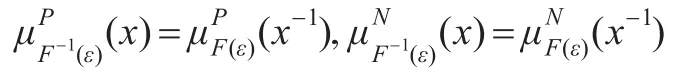
性质2.1设(F，A)和(K，B)是群G上的两个双极值模糊软集，则

3 双极值模糊软子群的等价刻画

本章中在文献[19]的基础上进一步给出群G上的双极值模糊软子群的一些等价刻画。

定义3.1[19]设(F，A)是群G上的双极值模糊软集，称(F，A)是G的双极值模糊软子群，如果∀ ε∈A，∀ x，y∈G有：

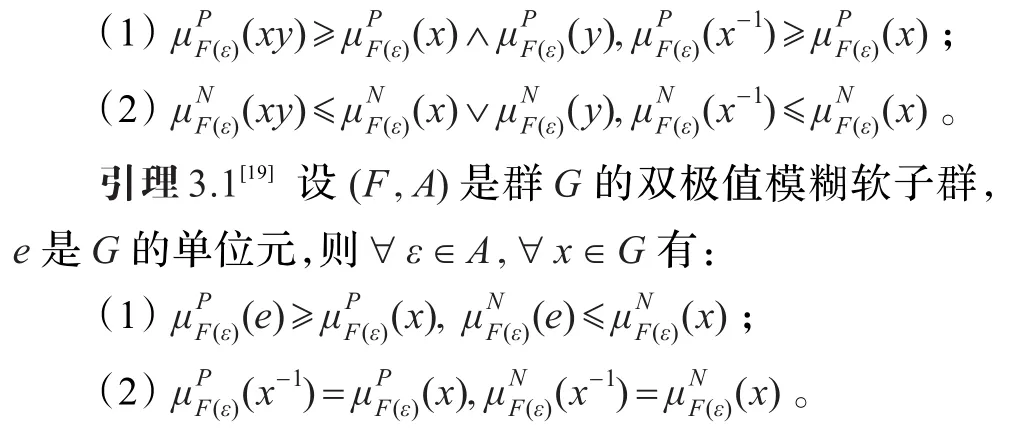
定理3.1[19]设(F，A)是群G上的双极值模糊软集，则(F，A)是G的双极值模糊软子群当且仅当∀ ε∈A，∀ x，y∈G有：

定理3.2设(F，A)是群G上的双极值模糊软集，则(F，A)是群G的双极值模糊软子群当且仅当(F，A)(F，A)(F，A)，(F，A)(F，A)-1。

证明由引理3.2、引理3.3及定义3.1即得。

定理3.3设(F，A)是群G上的双极值模糊软集，则(F，A)是群G的双极值模糊软子群当且仅当(F，A)(F，A)-1(F，A)。

证明必要性：(F，A)是群G的双极值模糊软子群，则由定理3.2可得(F，A)(F，A)(F，A)，(F，A)(F，A)-1。由性质2.1（4）得(F，A)=(F，A)-1，从而(F，A)(F，A)-1(F，A)。

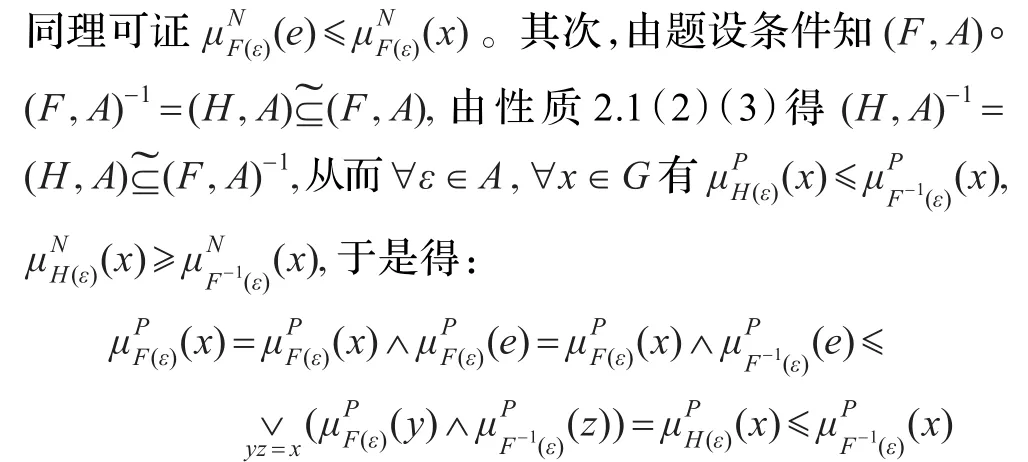
定理3.4设(F，A)是群G的双极值模糊软子群则(F，A)(F，A)=(F，A)。

根据性质2.1，定理3.2及定理3.4可得下面的推论。

推论3.1设(F，A)是群G上的双极值模糊软集，则(F，A)是群G的双极值模糊软子群当且仅当(F，A)(F，A)=(F，A)，(F，A)=(F，A)-1。

定理3.5设(F，A)和(K，B)是群G的双极值模糊软子群，且(F，A)(K，B)=(K，B)(F，A)，则(F，A)(K，B)是群G的双极值模糊软子群。

证明设(F，A)和(K，B)是群G的双极值模糊软子群，由推论3.1得：

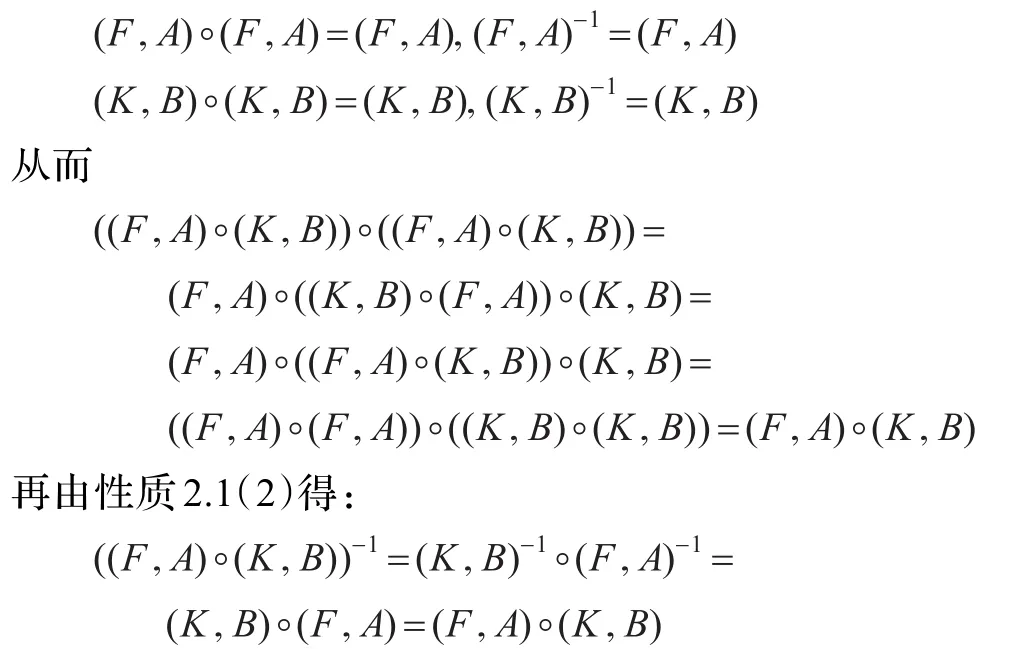
定义3.2[19]设(F，A)是群G上的双极值模糊软集，α∈[0，1]，β∈[-1，0]，∀ ε∈A定义：

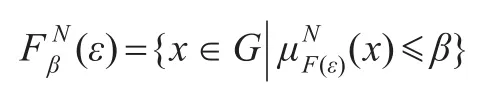
定理3.6[19]设(F，A)是群G上的双极值模糊软集，则(F，A)是G的双极值模糊软子群当且仅当∀ ε∈A，∀ α∈[0，]，∀ β∈[-1，0]，当F(ε)，F(ε)非空时，F(ε)，(ε)都是G的子群。

定义3.3[19]设(F，A)和(K，B)分别是X和Y上的双极值模糊软集，φ是X到Y的映射，ψ是A到B的映射，则称(φ，ψ)是X到Y的双极值模糊软映射。

定义3.4[19]设(F，A)和(K，B)分别是X和Y上的双极值模糊软集，(φ，ψ)是X到Y的双极值模糊软映射，定义Y上的双极值模糊软集(φ(F)，ψ(A))：∀ ε′∈ψ(A)，∀ y∈Y

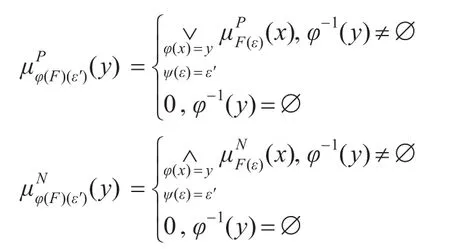
则称双极值模糊软集(φ(F)，ψ(A))是(F，A)在(φ，ψ)之下的像，记作(φ，ψ)(F，A)=(φ(F)，ψ(A))。

定义X上的双极值模糊软集(φ-1(K)，ψ-1(B))：∀ ε∈ψ-1(B)，∀ x∈X，

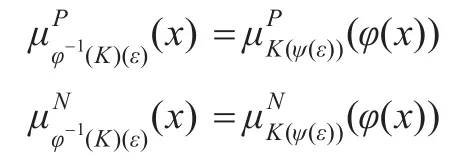
则称双极值模糊软集(φ-1(K)，ψ-1(B))是(K，B)在(φ，ψ)之下的原像，记作：

定义3.5[19]设(F，A)和(K，B)分别是群G1和G2上的双极值模糊软集，(φ，ψ)是G1到G2的双极值模糊软映射，若φ是G1到G2的群同态映射，则称(φ，ψ)是G1到G2的双极值模糊软同态映射。

定理3.7[19]设G1和G2是两个群，(F，A)是G1的双极值模糊软子群，(φ，ψ)是G1到G2的双极值模糊软同态映射，则(φ，ψ)(F，A)是G2的双极值模糊软子群。

定理3.8[19]设G1和G2是两个群，(K，B)是G2的双极值模糊软子群，(φ，ψ)是G1到G2的双极值模糊软同态映射，则(φ，ψ)-1(K，B)是G1的双极值模糊软子群。

4 双极值模糊正规软子群

设G是群，x，y∈G，规定xy=y-1xy，并称xy为x在y下的共轭变形。

定义4.1设(F，A)是群G的双极值模糊软子群，若∀ε∈A，∀x，y∈G有：

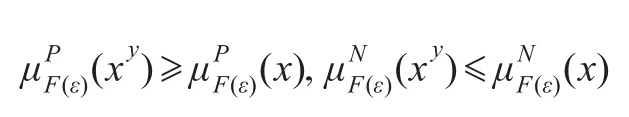
则称(F，A)是群G的双极值模糊正规软子群。

例设N是自然数集，G是四次对称群S4，A4是四次交代群。G上的双极值模糊软集(F，N)定义如下：是G上的双极值模糊集，这里：

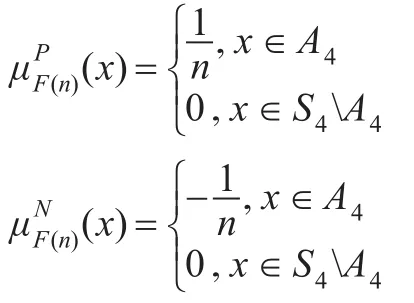
容易验证(F，N)是群G的双极值模糊软子群。又因为A4是S4的正规子群，所以对任意x，y∈G，有：xy∈A4⇔x∈A4，xy∈S4A4⇔x∈S4A4，从而(F，N)是群G上的双极值模糊正规软子群。

定理4.1设(F，A)是群G上的双极值模糊软集，则(F，A)是群G的双极值模糊正规软子群当且仅当∀ε∈A，∀α∈[0，1]，∀β∈[-1，0]，当集合(ε)，(ε)非空时，(ε)，(ε)都是G的正规子群。

(1)⇒(5)设(K，B)是群G上的任意双极值模糊软集，记(F，A)(K，B)=(H，C)，(K，B)(F，A)=(H1，C1)，其中C=A∩B=B∩A=C1。∀ε∈C，∀x∈G，

定理4.2设(F，A)是群G的双极值模糊软子群，则下列条件等价：

（1）(F，A)是群G的双极值模糊正规软子群。

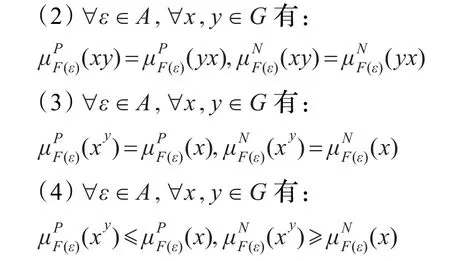
证明由引理4.1及定义4.1即得。

由定理3.5及定理4.2（5）可得下面的两个定理。

定理4.3设(F，A)是群G的双极值模糊正规软子群，(K，B)是群G的双极值模糊软子群，则(F，A)(K，B)是群G的双极值模糊软子群。

定理4.4设(F，A)和(K，B)都是群G的双极值模糊正规软子群，则(F，A)(K，B)也是群G的双极值模糊正规软子群。

定理4.5设(F，A)是群G的双极值模糊软子群，则(F，A)是群G的双极值模糊正规软子群当且仅当∀ε∈A，∀x，y∈G有：

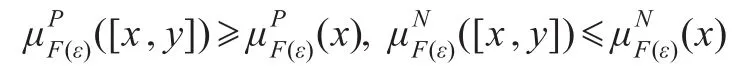
这里[x，y]是G的换位子。

证明必要性：设(F，A)是群G的双极值模糊正规软子群，则∀ε∈A，∀x，y∈G，

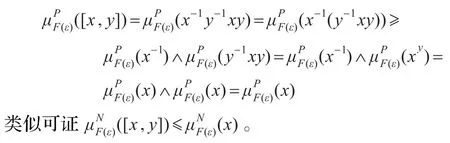
充分性：∀ε∈A，∀x，y∈G，因为(F，A)是群G的双极值模糊软子群，所以

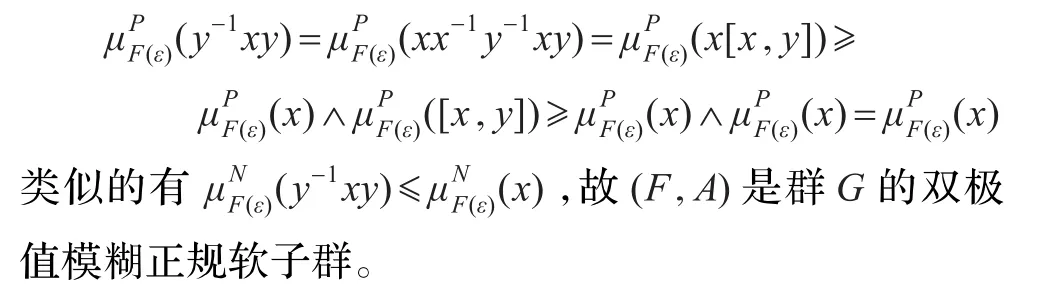
推论4.1设(F，A)是群G的双极值模糊软子群，e是G的单位元。如果∀ε∈A，∀x，y∈G，有：

则(F，A)是群G的双极值模糊正规软子群。

定理4.6设G1，G2是两个群，(φ，ψ)是G1到G2的双极值模糊软同态映射，且φ是G1到G2的满同态。若(F，A)是群G1的双极值模糊正规软子群，则(φ，ψ)(F，A)是群G2的双极值模糊正规软子群。

证明由定理3.7知(φ，ψ)(F，A)是群G2的双极值模糊软子群。∀ε′∈ψ(A)，∀y1，y2∈G2，因为φ是G1到G2的满同态，所以∃x1，x2∈G1使得φ(x1)=y1，φ(x2)=y2，从而由此可得：

定理4.7设G1，G2是两个群，(φ，ψ)是G1到G2的双极值模糊软同态映射。若(F，A)是群G2的双极值模糊正规软子群，则(φ，ψ)-1(F，A)是群G1的双极值模糊正规软子群。

证明由定理3.8知(φ，ψ)-1(F，A)是群G1的双极值模糊软子群。∀ε∈ψ-1(A)，∀x1，x2∈G1，

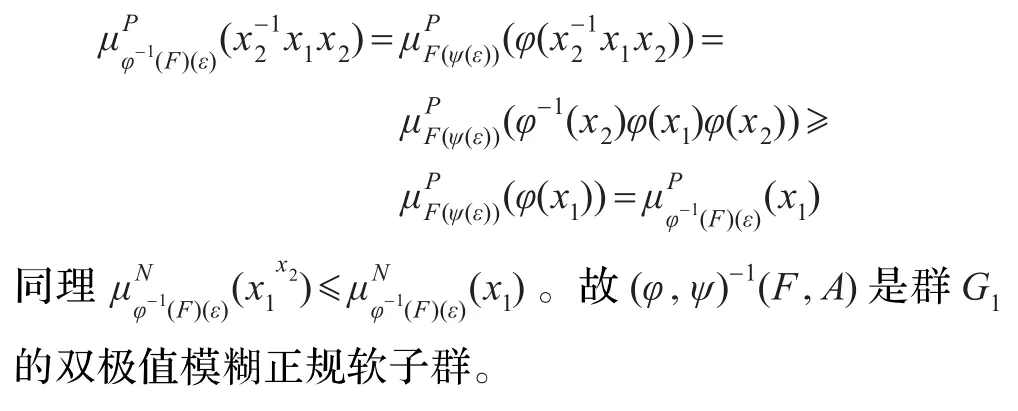
5 结束语

本文将双极值模糊软集理论应用到群上，定义了双极值模糊正规软子群，并研究了双极值模糊软子群和双极值模糊正规软子群的代数性质，使得对群的理论的研究又向前迈进了一步。利用这一定义方式，双极值模糊软集理论还可以应用到其他的代数系统中，比如环、域、模等等，使这些代数理论也得到进一步的发展。

[1]Molodtsov D A.Soft set theory-first results[J].Computers and Mathematics with Applications，1999，37（4/5）：19-31.

[2]Maji P K，Biswas R，Roy A R.Soft set theory[J].Computers and Mathematics with Applications，2003，45：555-562.

[3]Maji P K，Biswas R，Roy A R.Fuzzy soft sets[J].Journal of Fuzzy Mathematics，2001，9（3）：589-602.

[4]Ali M I，Feng Feng，Liu Xiaoyan，et al.On some new operations in soft set theory[J].Computers and Mathematics with Applications，2009，57：1547-1553.

[5]Aygünoglu A，Aygün H.Introduction to fuzzy soft groups[J].Computers and Mathematics with Applications，2009，58：1279-1286.

[6]Çağman N，Enginoğlu S.Soft matrix theory and its decision making[J].Computers and Mathematics with Applications，2010，59：3308-3314.

[7]Çağman N，Enginoğlu S.Soft set theory and uni-int decision making[J].European Journal of Operational Research，2010，207：848-855.

[8]Çağman N，Enginoğlu S，Çitak F.Fuzzy soft set theory and its applications[J].Iranian Journal of Fuzzy Systems，2011，8（3）：137-147.

[9]Aktaş H，Çağman N.Soft sets and soft groups[J].Information Science，2007，177（13）：2726-2735.

[10]Feng Feng，Jun Y B，Zhao Xianzhong.Soft semirings[J].Computers and Mathematics with Applications，2008，56：2621-2628.

[11]Jun Y B.Soft BCK/BCI-algebras[J].Computers and Mathematics with Applications，2008，56：1408-1413.

[12]Jun Y B，Lee K J，Zhang Jianming.Soft p-ideals of BCIalgebras[J].Computers and Mathematics with Applications，2009，58：2060-2068.

[13]Jun Y B，Lee K J，Khan A.Soft ordered semigroups[J].Mathematical Logic Quarterly，2010，56（1）：42-50.

[14]Zhang Jianming，Jun Y B.Soft BL-algebras based on fuzzy sets[J].Computers and Mathematics with Applications，2010，59：2037-2046.

[15]Atagün A O，Sezgin A.Soft substructures of rings，fields and modules[J].Computers and Mathematics with Applications，2011，61（3）：592-601.

[16]Manemaran S V.On fuzzy soft groups[J].International Journal of Computer Applications，2011，15（7）：38-44.

[17]Zhang Wenran.Bipolar fuzzy sets and relations：a computational framework for cognitive modeling and multiagent decision analysis[C]//Proceedings of IEEE Conference，1994：305-309.

[18]杨文华，李生刚.双极值模糊软集[J].计算机工程与应用，2012，48（35）：15-18.

[19]殷霞，廖祖华，章里程，等.双极值模糊（反）软子群[J].计算机工程与应用，2013，49（19）：58-62.

YIN Xia, LIAO Zuhua, ZHANG Licheng, ZHU Xiaoying

School of Science, Jiangnan University, Wuxi, Jiangsu 214122, China

The equivalent characterizations of bipolar-value fuzzy soft subgroup are investigated. The concept of bipolarvalue fuzzy normal soft subgroup based on the bipolar-value fuzzy soft subgroup is introduced and in the meantime, some of its properties and equivalent characterizations are discussed. Furthermore, the theorems of soft homomorphic image and pre-image of bipolar-value fuzzy normal soft subgroup are given.

bipolar-value fuzzy soft set; bipolar-value fuzzy soft subgroup; bipolar-value fuzzy normal soft subgroup;bipolar-value fuzzy soft homomorphism

YIN Xia, LIAO Zuhua, ZHANG Licheng, et al. Bipolar-value fuzzy soft subgroups and bipolar-value fuzzy normal soft subgroups. Computer Engineering and Applications, 2014, 50（17）：74-79.

A

O153

10.3778/j.issn.1002-8331.1401-0055

国家自然科学基金（No.11301227）；江苏省自然科学基金青年基金项目（No.BK 20130119）。

殷霞（1975—），女，讲师，主要研究领域为有限群理论、模糊与粗糙代数；廖祖华（1957—），男，教授，主要研究领域为模糊与粗糙代数、广义逆理论及应用、人工智能等；章里程（1972—），男，副教授；朱晓英（1964—），女，副教授。E-mail：yin-xia1975@aliyun.com

2014-01-06

2014-03-20

1002-8331（2014）17-0074-06

CNKI网络优先出版：2014-06-20,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1401-0055.htm l