泊松过程和排队论在银行排队问题中的研究

邓秋玲，韦新星

（广西大学数学与信息科学学院，广西南宁530004）

泊松过程和排队论在银行排队问题中的研究

邓秋玲，韦新星

（广西大学数学与信息科学学院，广西南宁530004）

银行排队现象屡见不鲜，如何缓解和控制银行的排队问题一直是顾客和银行管理者共同关心的问题.基于泊松过程和排队论处理银行排队问题，确定当前银行所需的服务窗口数目，理论计算结果与银行当前的实际情况相符.验证了二者的结合是解决银行排队问题的一种实用新途径，且能够为银行的窗口数目设置、最优系统问题提供决策支持.

银行；排队问题；泊松过程；排队论；最优系统

经济发展给银行业带来繁荣景象的同时，也带来了一些不可避免的问题.其中最为突出的是银行的排队问题[1].针对该问题，目前很多银行都采取了一些相应措施，诸如调整银行网点的设置、引导顾客使用自助设备等，但效果均不明显.

排队论[2]是研究系统由于随机因素干扰而出现排队现象的一门学科，能够在研究各种排队系统概率规律性的基础上，解决相应排队系统的最优设计和最优控制问题.将泊松过程与排队论结合，并应用到银行窗口服务中研究，是解决银行排队问题的一次新角度尝试.

1 相关理论

1.1 泊松过程

泊松过程[3-4]是应用最广泛的一类随机过程，它常用来描述排队系统中顾客到达的过程.

记N（t）为时间区间[0，t）（t＞0）内发生的事故数，如果N（t）是一个随机变量，那么就称为一个随机过程.

泊松过程的定义为：对于随机过程{N（t），t≥0}，如果满足

①N（0）=0；

②具有独立增量；

③在任何长度为t的时间内，发生的事件数服从参数为λt的泊松分布.

则称上述过程为泊松过程，且λ为其强度.

1.2 排队系统与泊松过程[5]

如果N（t）为时间区间[0，t）（t＞0）内到达系统的顾客数，那么N（t）是一个随机变量，且是一个随机过程.若该随机过程满足：

①在不相重叠的区间内，顾客的到达数是相互独立的；

②在时间区间[t，t+Δt）内，顾客的到达与时间起始点t无关，而只与区间长度Δt有关；

1.3 排队论基本知识[6]

一般的排队系统由三个基本部分组成：输入过程、排队规则和服务机构.当研究的是多服务台单队列队时，排队过程见图1.

图1 多服务台单队系统Fig.1One team system with multi service platform

银行排队问题是一个典型的并列多服务台单队排队系统，可表示为M/M/s模型.它是指输入过程为泊松输入、服务时间服从负指数分布、共有s个服务窗口的排队系统模型.现对该模型所用到的一些数量指标符号作下述规定：

L：平均队长，表示系统中的顾客数，是排队等候的顾客和正在接受服务的顾客的总和.

Lq：平均列队长，表示系统中排队等候的顾客数.

W：平均逗留时间，包括等待时间和服务时间.

Wq：平均等待时间，也称平均排队等待时间.

P0：系统到达平衡时，所有服务台空闲的概率.

λ：顾客到达的平均速率，即单位时间内平均到达的顾客数.

μ：平均服务速率，即单位时间内服务完毕离去的顾客数.

ρ：服务强度，表示每个服务窗口单位时间内的平均服务时间，有公式成立，且只有当ρ＜1时才不会排成无限的队列.

从状态间的转移关系分析M/M/s模型，可以得到：

用递推法解上述差分方程，得到状态概率：

于是求得各指标如下：

平均队长

平均列队长

平均逗留时间

根据上述各表达式可以知道，只要确定了顾客到达的平均速率λ和平均服务速率μ，即可计算出W和Wq，进而确定服务窗口数量.

1.4 排队系统最优化

银行排队系统包括顾客和银行两方面.顾客总是希望逗留时间越短越好，服务窗口数目越多越好、服务效率越高越好，而这些往往会使得银行的服务费用大大增加，有损银行的利益.因此，在考虑银行排队的优化问题时，应从顾客和银行双方的利益出发，以费用作为指标，进行考察[7].

至于最佳服务台数目s*的确定，在M/M/s模型中，服务台数可控，取单位时间全部费用的期望值的最小者，即

其中s为服务台数，cs是每个服务台单位时间的成本，cw是每个顾客在系统停留单位时间的费用.cs和cw均可人为给定.运用边际分析法有

结合（6）和（7）式并化简得

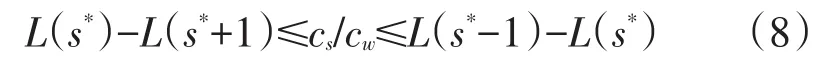
此时，依次求s=1，2，…时的L值，并计算相邻两个L值的差，鉴于cs/cw是已知数，故可根据该数落在哪个不等式的区间来确定最优服务台数s*.

2 基于泊松过程和排队论的银行排队问题分析

2.1 数据处理

以某银行为研究对象，对其进行多次实际调查和统计，选取其中一天上午9点30分到11点30分内所到达顾客的相关信息进行汇总整理，得到样本数据.部分数据见表1.

表1 各时间段所到达的顾客数Tab.1Number of customers who arrive at each time

2.2 顾客流量分析和服务时间分析

结合表1的数据，运用SPSS统计软件进行单样本K-S检验，结果见表2.

表2 单样本Kolmogorov-Smirnov检验Tab.2Kolmogorov-Smirnov test of single sample

a.检验分布为Poisson分布.

b.根据数据计算得到.

由于P=0.992＞0.05，故可认为银行顾客流量过程服从泊松分布.同时还可以知道，顾客到达的平均速率λ=5（人/10分钟）=0.5（人/分钟）.

同理可验证银行排队系统的服务时间服从负指数分布，且还可得到每个窗口的平均服务速率μ=3（人/10分钟）=0.3（人/分钟）.

2.3 各项指标计算值[8]

结合公式（1）-（5），可以得到s取不同值时各指标对应的计算值.

窗口空闲概率

平均队长L=3.772+2-0.833=5.438（人）

④当s=4时，P0=0.186，Lq=0.074（人），L=1.742（人），Wq=0.148（分钟），W=3.484（分钟）.

⑤当s=5时，P0=0.188，Lq=0.015（人），L=1.680（人），Wq=0.030（分钟），W=3.360（分钟）.

现将各指标计算值列入表3.

由表3知，当银行设置3个服务窗口时，减少排队人数3.772-0.377=3.395≈3人，排队问题可以得到较好解决；但当设置4个服务窗口时，减少的排队人数0.377-0.074=0.303人，排队问题没能得到很好解决.

2.4 银行排队系统的最优化

鉴于经验分析，假设cs为1（元/分钟），cw为0.8（元/分钟）.结合上表和式子（6）、（8），得到表4.

表3 各指标计算值Tab.3Calculated values of each index

表4 排队系统总费用Tab.4Total cost of queuing system

则由于cs/cw=1.25，落在区间（0.573，3.393）内，所以s*为3.且从上表中的最右边一列也可验证，当设置3个服务窗口时的总费用是最小的，即

minZ（s*）=Z（3）=css+cwL=13+0.82.045=4.636（元）

综上，在该时间段内，当该银行设置的服务窗口数目为3时，顾客和银行的利益达到最优平衡.同时，根据观察得知，此结论与当前银行的实际情况相符.

（1）将泊松过程与排队论结合，验证了在银行排队系统中，顾客流量服从泊松分布，而窗口服务时间服从负指数分布.

（2）通过对基于泊松过程和排队论的银行窗口排队问题的实际应用，验证了二者的结合是解决银行排队问题的一种新途径，且能够为银行的窗口数设置、最优系统问题提供决策支持.

3 结论

[1]高斯博.银行排队问题及窗口设置优化研究[J].财政金

[2]融,2011(7):80-81.王兴贵,焦争昌.基于排队论的银行排队问题研究[J].湘

[3]潭师范学院学报:社会科学版,2008,30(1):58-60.王东升,刘玉堂.泊松过程在排队论中的应用[J].河南机

[4]电高等专科学校学报,2007,15(4):121-125.盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等

[5]教育出版社,2008:356-357.

[6]熊伟.运筹学[M].北京:机械工业出版社,2005:193-212.钱颂迪,顾基发,郭耀煌,等.运筹学[M].北京:清华大学出

[7]版社,2005:325-337.肖立顺,石玉文,黄勇博.银行排队系统的随机分析[J].

[8]信息与电脑,2009(8):15.覃志奎.基于银行排队问题的数学模型及求解[J].大众科学,2008(3):24-26.

责任编辑：毕和平

Study of Poisson Process and the Queuing Theory in the Bank Queuing Problem

DENG Qiuling，WEI Xinxing
（College of Mathematics and Information Science，Guangxi University，Nanning 530004，China）

Bank queuing phenomenon is common,and it’s the concern that how to alleviate and control the bank queuing problem for both customers and the bank managers.The article deals with the problem of bank queuing based on the Poisson process and the Queuing theory,and determines the number of service window.The result shows that it’s the same with the actual.Then we conclude that the combination of Poisson process and Queuing theory is a practical new way to solve the problem of bank queuing,and can provide decision support for the setting of the number of windows as well as the optimal system problems.

bank；queuing problem；Poisson process；Queuing theory；optimal system

O 211.6

A

1674-4942（2014）01-0011-04

2013-09-15

广西自然科学基金（2012GXNSFBA053010）