基于投影神经网络求解凸规划问题的二分法

刘勇为，胡剑峰，王平

（海南师范大学数学与统计学院，海南海口571158）

基于投影神经网络求解凸规划问题的二分法

刘勇为，胡剑峰*，王平

（海南师范大学数学与统计学院，海南海口571158）

将投影梯度神经网络方法和二分法相结合，提出了一种求解凸规划的新算法，并证明了该算法的收敛性.

凸规划；二分法；神经网络

近年来，用神经网络来解决优化问题已经取得了很多重要的成果，其中很多已经被应用到优化领域和工程控制中.

1985年，Tank和Hopfield[1]首次提出了一类神经网络模型来解决线性规划问题，但其平衡点不能保证收敛到线性规划问题的最优点.后来，Kennedy和Chua[2]提出了一类求解非线性规划的神经网络.该模型利用了罚函数，仅当惩罚参数为无限大时，才有可能得到问题的最优解.为了避免使用罚参数，Zhang和Constantinides[3]基于Lagrange乘子法建立了求解约束优化问题的网络模型，该模型在目标函数是严格凸时能保证收敛到问题的最优解.

基于投影理论的投影神经网络最近被提出来用来解决一般凸规划问题，如：Liang[4]和Gao[5]建立了求解约束优化问题的投影神经网络模型；Yang[6]提出了凸规划的投影神经网络.本文在文献[6]的基础上，首先通过构造Lyapunov函数和利用LaSalle不变原理，给出了投影神经网络模型稳定性和收敛性的一种新的证明过程；其次结合二分法的思想，提出一种求解凸规划问题的二分投影神经网络模型，并给出了算法的收敛性证明.

1 问题和模型建立

考虑如下凸规划问题

其中，f

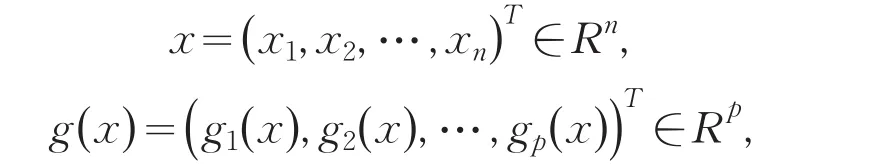
（x）和gi（x）（i=1，2，…，p）在Rn→R上是2阶连续可微的凸函数，A∈Rm×n,b∈Rn和

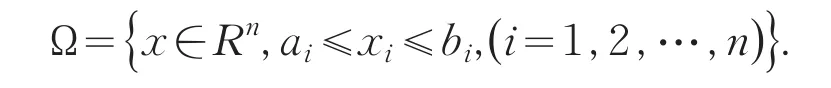
对于问题（1），考虑下面的子问题[6]

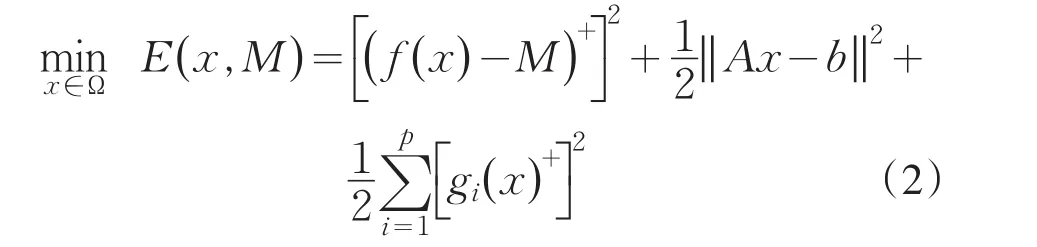
和相应的投影梯度神经网络

其中

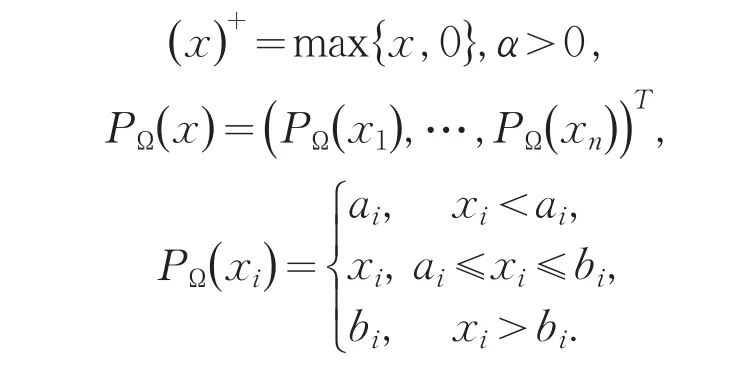
2 投影神经网络稳定性和收敛性分析

本节通过构造Lyapunov函数和利用LaSalle不变原理，给出了投影神经网络模型（3）的全局稳定性和收敛性的一种新的证明过程.

证明令x*是问题（2）的最优解，考虑如下的Lyapunov函数

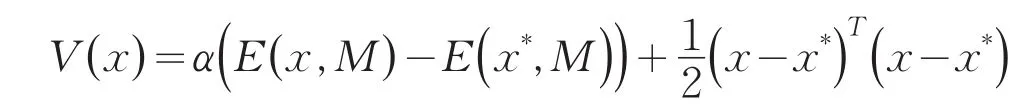
显然V（x）是Ω上的连续可微的凸函数，并且对

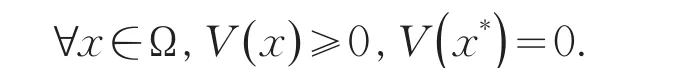
根据投影理论和E（x，M1）是可微的凸函数，很容易得到

由此，可以得到神经网络（3）对于任意的初始点是Lyapunov意义下稳定的.

证明（i）先证存在唯一连续解.

（ii）再证Ω是神经网络模型（3）的不变集，即

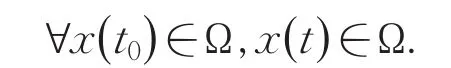
从而

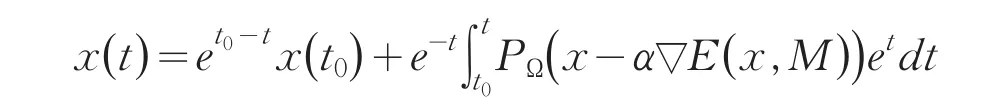
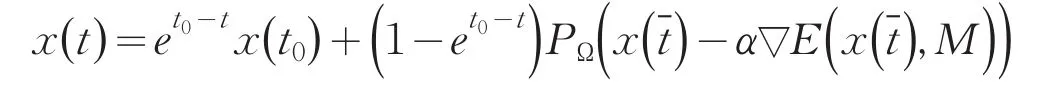
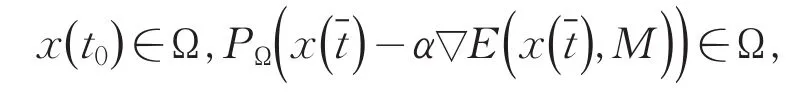
（iii）最后证明x（t）在[t0，T）上是有界的.

令x*是问题（2）的最优解.由V（t）的定义及V（t）沿着轨线x（t）是不增的，有

从而有

因此，x（t）是有界的，故T=+∞.

综合（i）、（ii）和（iii）即得到定理2的证明.

定理3令Ωe为神经网络（3）的平衡点集，Ω*为凸规划问题（2）的最优解集，则Ωe=Ω*.

证明x*是凸规划问题（2）的最优解，即x*∈Ω*，等价于

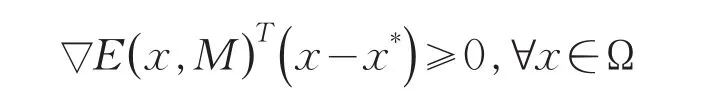
上式又等价于

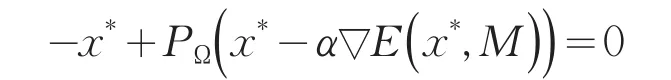
故Ωe=Ω*.

根据LaSalle不变原理，于是有下式成立

令

又因为V1（x）是连续的，故有

而

3 基于投影神经网络的二分法

基于上一节的投影神经网络模型，结合二分法的思想，给出了一个求解问题（1）的二分投影神经网络模型，并给出了算法的收敛性证明.

定理5设Lk和Uk分别是问题（1）的最优值的下界和上界，即，将带入子问题（2），得到相应的神经网络模型（3）的平衡点.如果，则有如果，则有

根据上面的定理5，给出了求解问题（1）的二分投影神经网络算法.

算法1

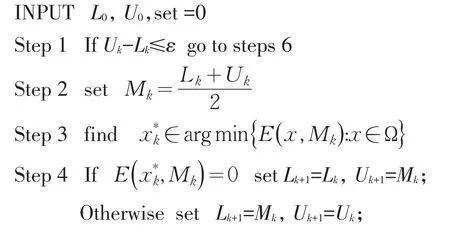
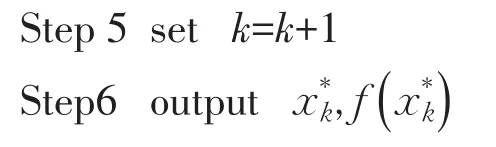
定理6令x*是凸规划问题（1）的最优解，L0和U0分别是问题（1）的最优值的下界和上界，则基于投影神经网络求解问题（1）的二分法得到的序列满足

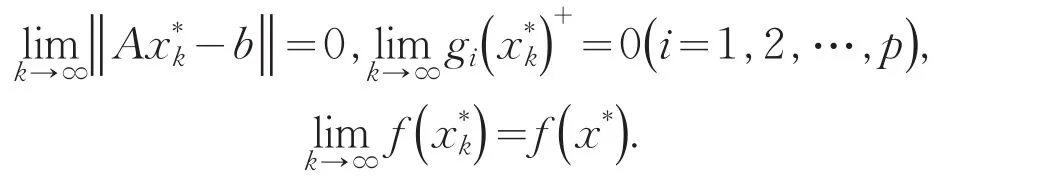
证明对任意k≥0，有

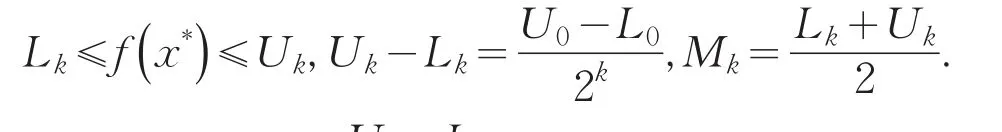
而

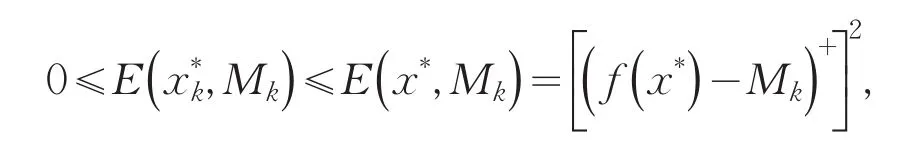
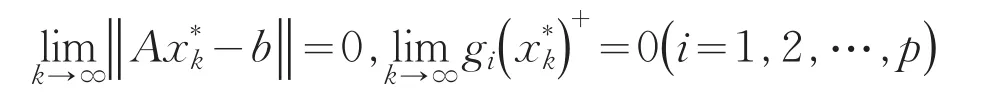
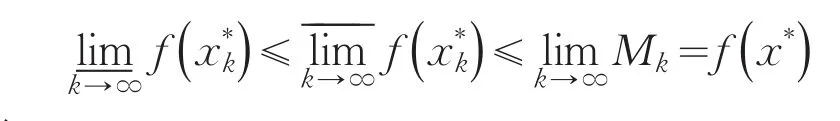
而

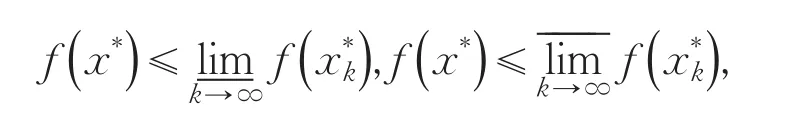
故有

即

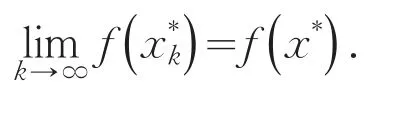
[1]Tank D W,Hopfield J J.Simple‘neural’optimization network:an A/D converter,signal decision circuit and a linear programming circuit[J].IEEE Trans Circuits Syst, 1986,33:533-541.

[2]Kennedy M P,Chua L O.Neural networks for nonlinear programming[J].IEEE Trans Circuits Syst,1988,35:554-562.

[3]Zhang S,Constantinides A.Lagrange programming neural networks[J].IEEE Transaction on Circuits and Systems-II:Analog and Digital Signal Processing,1992,39(7):441-452.

[4]Liang X,Wang J.A recurrent neural network for nonlin-ear optimization with a continuously differentiable objective functions and bound constraints[J].IEEE Transactions on Neural Networks,2000,11(6):1251-1262.

[5]Gao X.A novel neural network for nonlinear convex programming[J].IEEE Transactions on Neural Networks, 2004,15:613-621.

[6]Yang Y,Cao J.A feedback neural network for solving convex constraint optimization problems[J].Appl Math Comput,2008,201:340-350.

责任编辑：毕和平

A Bisection Method for Convex Programming Based on the Projection Neural Network

LIU Yongwei，HU Jianfeng＊，WANG Ping
（College of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

In this paper,a new algorithm for convex programming is proposed by combining projection neural network with bisection method.The convergence of the algorithm is proved.

convex programming；bisection method；neural network

O 221.1

A

1674-4942（2014）01-0015-03

2013-10-25

*通讯作者