新分数阶混沌系统及异结构同步

潘红

（山西工程职业技术学院基础部，山西太原030002）

新分数阶混沌系统及异结构同步

潘红

（山西工程职业技术学院基础部，山西太原030002）

文章提出了一个新的分数阶三维混沌系统，利用分数阶稳定性理论给出证明，画出其吸引子相图验证了其具有混沌学行为；同时也在理论上证明了该系统与分数阶chen系统异结构同步，并运用matlab软件数值模拟仿真得出误差系统演化曲线图，充分说明了两系统达到有效同步.

分数阶；吸引子；混沌同步

自从分数阶微积分理论被引入混沌研究中，对分数阶混沌系统及其同步的研究就逐步的被研究者们所关注，成为了研究的热点问题，文献[1-2]发现分数阶chen系统，分数阶Lorenz系统，分数阶Rosslor系统，文献[3-4]对分数阶混沌系统同步控制进行深入的研究.发现在各领域中分数阶系统是系统通常的存在方式，而整数阶系统只是一种理想化状态，所以对分数阶混沌系统的研究更加具有实际的意义，应用性更强.

本文提出了一个新的三维混沌系统，利用分数阶稳定性理论给出证明，画出其吸引子相图，验证了其混沌学行为；同时也对该系统与分数阶chen系统异结构同步给出了理论推导，运用matlab软件数值模拟仿真误差系统相图，充分说明了误差系统在原点渐进稳定，两系统达到同步，为分数阶混沌系统及其同步的研究提供一些理论依据.

1 分数阶微分的定义

在分数阶微积分的研究过程中，对分数阶导数的概念有多种定义，本文采用Caputo微分定义来研究分数阶混沌动力学行为，Caputo微分定义为

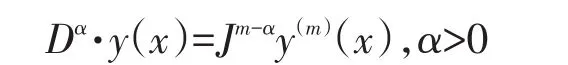
这里m=[α]，为第一个不小于α的整数，y（m）为y的m阶导数，Jβ是β阶Riemann-Liouville积分算子，即

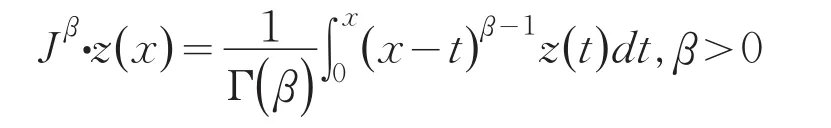
其中Γ（β）是Gamma函数.Dα*通常称为α阶Caputo微分算子.

2 分数阶系统稳定理论

引理[5]考虑线性分数阶系统：

其中X=（x1，x2，x3…xn）为系统状态变量，A为系数矩阵.

3 新的三维分数阶混沌系统

新的三维分数阶混沌系统：

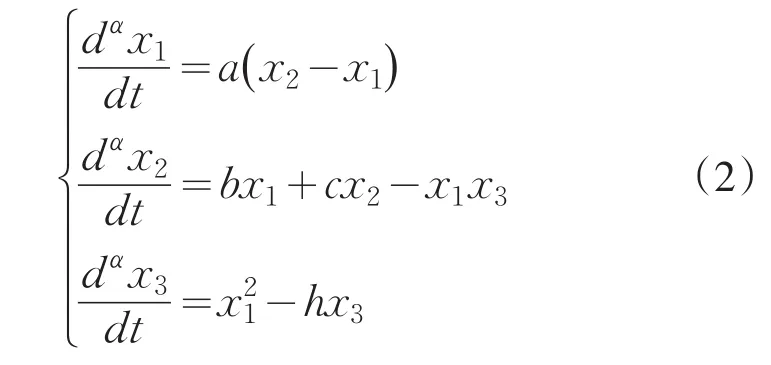
其中x1，x2，x3为系统的状态变量，系统参数a=20，b= 14，c=10.6，h=2.8，α为微分阶数dα=Dα为微分算子.

1）讨论系统为整数阶时系统的特性.

当α=1，初值为（20，20，20），通过LE软件包检算得出lyapunov指数为λL1=2.3554，λL2=3.0354×104，λL3=-14.5561.

系统的分形维数为

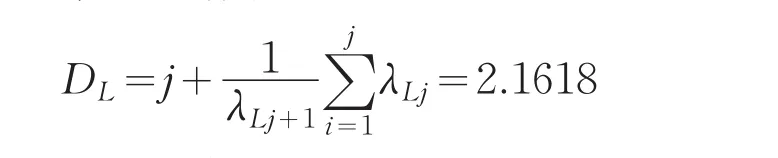
由上可推得，当α=1时，系统是混沌的，吸引子相图如下：

2）当0＜α＜1时，系统（2）的平衡点为：

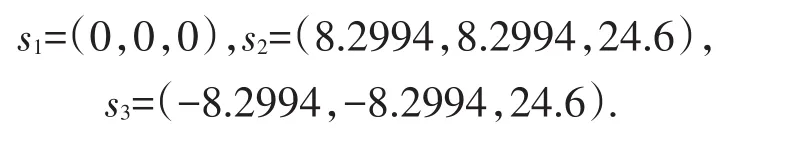
在平衡点s1，对系统（2）对应的Jacobian矩阵为

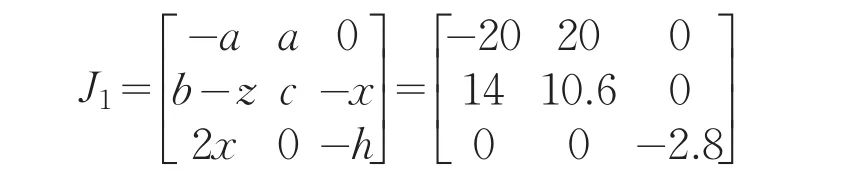
令det（J1-λI）=0，得到相应的特征根λ11=-2.8，λ12= 17.9736，λ13=-27.3736，这里两个负实根，一对正实根.根据Routh2Hurwitz条件，可得平衡点s1=（0，0，0）是不稳定的鞍点.

因为s2=（8.2994，8.2994，24.6）与s3=（-8.2994，-8.2994，24.6）关于z轴对称，若（a1，a2，a3）是方程的解，那么（-a1，-a2，-a3）也是方程的解，所以s2，s3具有相同的性质，相同的特征根.

在平衡点s2，采用同样的方法可求得其相应的特征根λ21=-18.6839，λ22=3.2419+11.7027i，λ23= 3.2419-11.7027i，这里一个特征根是负实根，一对共轭复根.根据Routh2Hurwitz条件，可得平衡点s2是不稳定的鞍点.则s3也是不稳定的鞍点.

可计算出

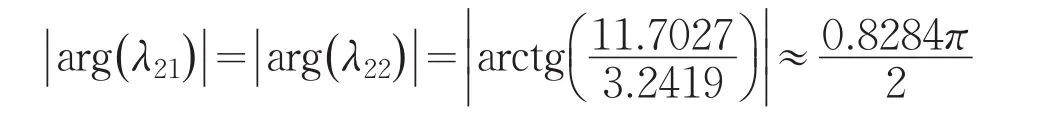
所以由引理1可知，系统（2）在0.8284＜α＜1时是混沌的.

利用预估校正法对该分数阶混沌系统的进行离散化，运用Matlab软件，进行数值模拟计算，得到结果为：当参数a=20，b=14，c=10.6，h=2.8时，0.8284＜α＜1时，该分数阶系统是混沌的.α=0.90，取初始值x0=1，y0=1，z0=2时，该系统的吸引子相轨迹图见图1.

4 分数阶混沌系统与分数阶chen系统异结构同步

驱动系统为

系统参数a=20，b=14，c=10.6，h=2.8响应系统为受控的分数阶chen系统u=u1，u2，u3为控制器

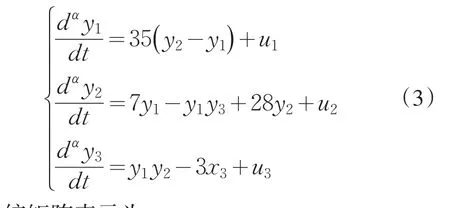
驱动系统矩阵表示为

响应chen系统矩阵表示为

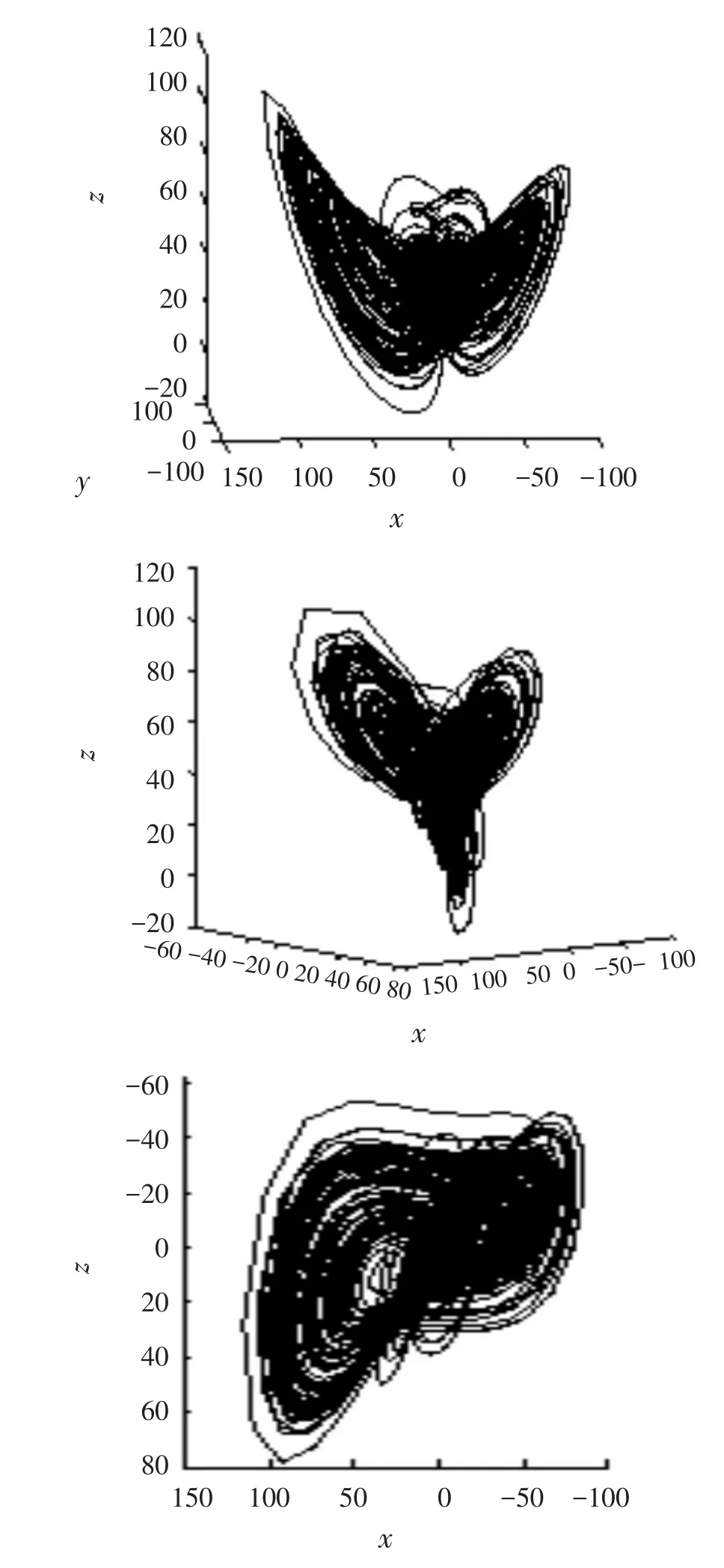
图1 α=0.90时的该分数阶混沌吸引子Fig.1The fractional chaotic attractor when α=0.90

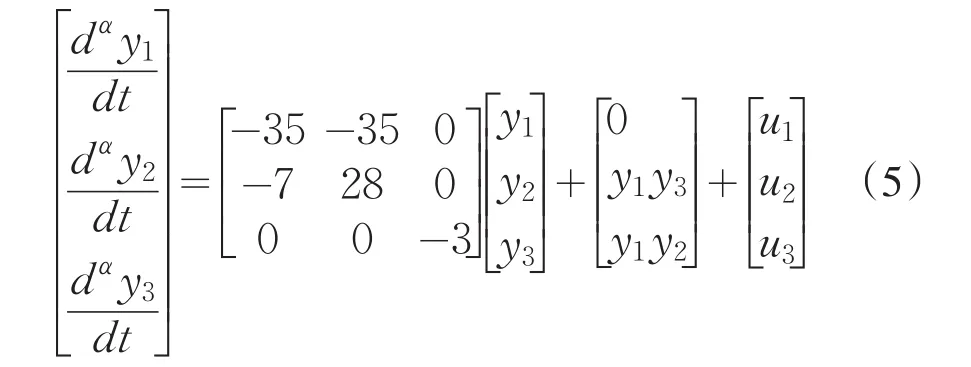
选取控制器

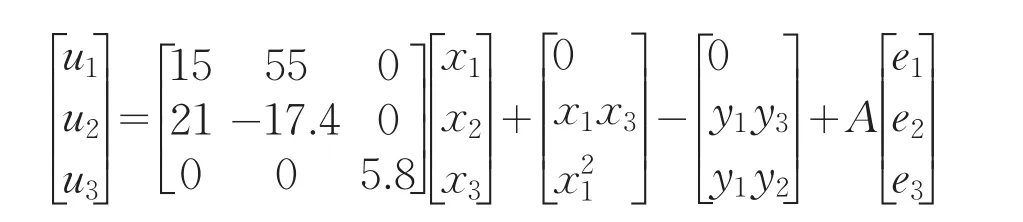
其中ei=xi-yi，i=1，2，3

用驱动系统（4）减去响应系统（5）得误差系统为：

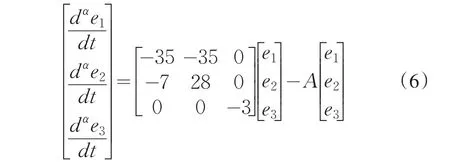
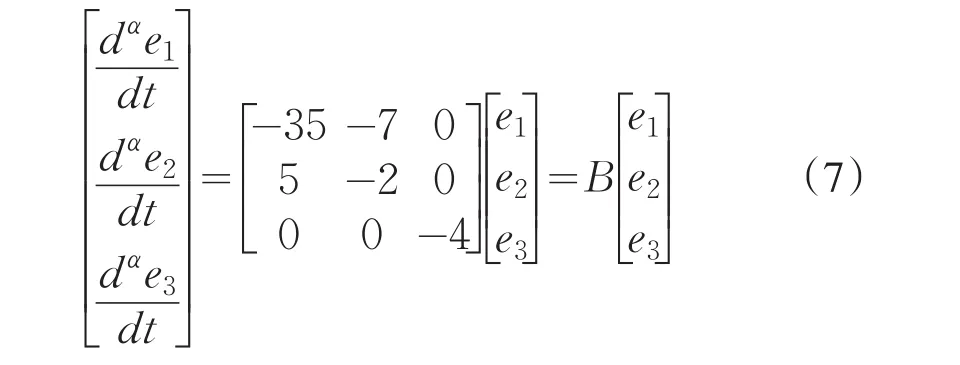
通过计算的矩阵B的特征值分别为

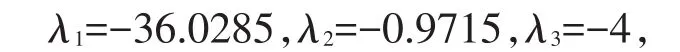
采用预估-校正解法，进行数值模拟，α=0.90，时间步长为0.01，状态初始值x1（0）=2，x2（0）=0，x3（0）=0，y1（0）=4，y2（0）=10，y3（0）=6；图2是误差系统演化曲线，可见系统（4）和（5）渐进同步.

5 结论

本文利用分数阶稳定性理论证明了一个新的分数阶三维动力系统的混沌特性，画出其吸引子相图来验证了其具有混沌学行为；同时也给出了该系统与分数阶chen系统异结构同步理论推导，并运用matlab软件进行数值模拟仿真得出误差系统演化相图，充分说明了误差系统在原点渐进稳定，两系统达到同步，为分数阶混沌系统及其同步的研究提供一些理论依据.

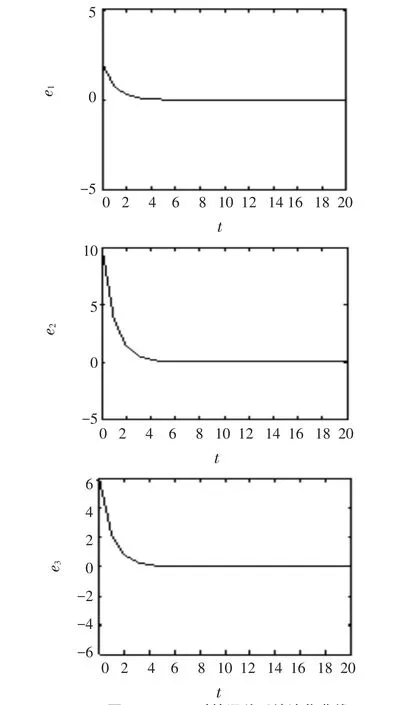
图2 α=0.90时的误差系统演化曲线Fig.2The evolution curve of the error system when α=0.90

[1]Lu J G.Nonlinear observer design to synchronize fractional-order chaotic system via a scalar transmitted signal[J]. Physica A,2006,359:107-118.

[2]Wu X J.Chaos in the fractional order unified system and its synchronization[J].Chinese physics,2007,16(7):392-401.

[3]Zhou T S,Li P.Synchronization in fractional—order differential systems[J].Physica D,2005,212:111-125.

[4]孙宁,张化光,王智良.基于分数阶滑模面控制的分数阶超混沌系统的投影同步[J].物理学报,2011,60（5）:1-7.

[5]胡建兵.分数阶混沌稳定性理论及同步方法研究[D].太原:中北大学,2008.

责任编辑：毕和平

Study of a New Fractional-Order Chaotic System and Different Structure Synchronization

PAN Hong
（Department of Basic，Shanxi Engineering Vactional College，Taiyuan 030002，China）

In this paper,a new fractional-order three dimensional chaotic syetem is presented,it is proved that this system is chaotic system based on the stable theory for fractional linear systems,Chaos behavior is given with chaotic attractor phase diagram,and it also proved that this system has different structure synchronization with Chen system.Phase diagrams of error system show that two system synchronize by matlab.

Fractional order；Chaotic attractor；Chaotic synchronization

O 415.5

A

1674-4942（2014）01-0007-04

2013-12-15

国冶金教育协会“十二五”高等教育科学研究课题（Yzy1127）