强度折减法计算边坡稳定性中弹性模量和泊松比的取值研究

潘新恩

（重庆交通大学河海学院，重庆400074）

强度折减法计算边坡稳定性中弹性模量和泊松比的取值研究

潘新恩

（重庆交通大学河海学院，重庆400074）

为探究强度折减法中弹性模量与泊松比取值对边坡稳定性系数的影响，采用有限元强度折减法，在强度参数折减的同时，根据公式调整弹性模量与泊松比的取值，所得到的边坡稳定性系数 ，与保持弹性模量和泊松比不变所得到的边坡稳定性系数对比，发现弹性模量与泊松比取值的变化对边坡稳定性系数计算结果影响很小，表明在采用有限元强度折减法计算边坡稳定性系数时只需对强度参数进行折减，不需要考虑弹性模量与泊松比取值的变化。

边坡稳定分析；安全系数；强度折减法；弹性模量；泊松比

边坡稳定、土压力和地基承载力是岩土力学中的三大经典问题［1－2］。边坡的稳定分析常用的方法主要有极限平衡条分法和有限元强度折减法［3－10］等。极限平衡法在工程实践中积累了丰富的使用经验，但是使用时需要做较多的假定，与实际存在不符，使得它在应用中受到一定的限制。有限元强度折减法则不需要做出任何假定，不仅能满足力的平衡条件，而且还可以求出土体的应力应变关系，考虑土体的非线性本构关系，而且可以直观的显示坡体失稳时滑动面的形状和位置。因此，采用有限元强度折减法进行边坡的稳定分析研究正成为新趋势［11］。

但是，在采用有限元强度折减法计算安全系数时，众多学者都是假定刚度参数 E和ν是不变的，仅仅对强度参数 c和φ折减，没有考虑随着强度参数的降低，应对刚度参数 E和ν做相应调整。已有研究结果表明：边坡的稳定与变形之间关系密切，坡体在失稳的同时常出现较大的垂直沉降与侧向变形的情况［12］。文献［11］认为由于弹性系数对变形有很大的影响，所以其对边坡安全系数还是有一定影响的。文献［13］指出若不调整弹性模量和泊松比，安全系数的计算结果有影响。文献［14］指出了对土体刚度参数进行调整的必要性，认为在对边坡土体的抗剪强度参数进行折减的同时，必须根据某一种方法对土体的刚度参数进行相应的调整，这样计算出来的安全系数才是合理的。因此笔者认为有必要探究清楚弹性模量与泊松比的取值变化对边坡稳定安全系数有何影响、以及影响的程度大小。

1 计算原理、方法及研究思路

1.1 有限元强度折减法原理

英国科学家Zienkiewicz在20世纪70年代就提出了在有限元中采用增加荷载或降低岩土强度的方法来计算岩土工程的极限荷载和安全系数［4］。有限元强度折减法的原理就是首先选取一个折减系数Fi，根据式（1）对原土体强度参数c和φ进行折减得到一组新的强度参数 c′和φ′，然后将得到的 c′和φ′代入有限元中进行分析，如此反复计算直到边坡达到临界破坏状态，把此时对应的折减系数作为安全系数 Fs。其公式如下：

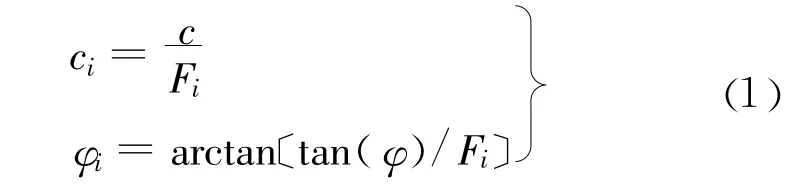
赵尚毅、郑颖人［15］等通过比较传统极限平衡法和有限元强度折减法的安全系数定义，认为两者的安全系数具有相同的物理意义，在本质上是一致的。因此，强度折减理论应用于边坡稳定分析是可行的。

1.2 本构关系与屈服准则的选取

有限元极限分析法所采用的本构模型为理想弹塑性模型。岩土工程分析中常选用的准则有摩尔－库仑准则和Drucker－Prager准则（简称D－P准则）两类。ANSYS采用的是摩尔－库仑不等角六边形外接圆D－P准则（在本文中简称DP1准则）。D－P准则可定义为：

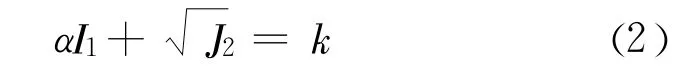
式中：I1，J2是应力张量的第一不变量和应力偏张量的第二不变量，α，k是与岩土材料强度参数有关的常数，不同的α，k在π平面上代表不同的圆，各准则的α，k见表1。

ANSYS中采用的是DP1准则，在实际工程计算中得到的结果是偏不安全的［8］。为了能够使用其他的屈服准则，可以利用DP1准则的α和κ与其他准则的α和κ对应相等这一条件，把在需要使用的准则中的强度参数，反算出来DP1准则中对应的强度参数后再带入ANSYS中，才能在ANSYS中是使用该准则。

表1 各屈服准则参数换算表［2，9］

安全系数的大小与计算所采用的屈服准则关系密切，采用不同的准则计算出来的安全系数是不一样的［10］。根据以往研究，采用由徐干成、郑颖人（1990）提出的摩尔－库仑等面积圆屈服准则（DP3）和平面应变非关联法则下摩尔－库仑匹配圆屈服准则（DP4）的计算结果精度相对较高。故本文在进行边坡稳定计算时，通过转化将DP1屈服准则转化为DP3和DP4准则，使计算结果更为精确，方便与传统极限平衡法作比较。

1.3 边坡破坏的判据

如何根据有限元计算结果来判断边坡是否达到极限破坏状态是采用有限元强度折减法分析边坡稳定性所面临的一个关键性问题［9］。边坡失稳判据的选取影响到安全系数计算的准确性，现在常用的失稳判据［3－6］主要有：（1）有限元计算不能收敛；（2）坡体内部塑性区从坡底到坡顶贯通；（3）边坡产生很大且无限发展的位移突变和塑性变形。

本文以边坡产生很大且无限发展的位移突变和塑性变形作为判别边坡失稳的标志。此时有限元计算也会出现计算不收敛和坡体塑性区的贯通［9］。

1.4 考虑刚度参数调整的方法

对刚度参数 E和ν做相应调整，基于一个基本的假定，即对于岩石类材料，若其满足摩尔 －库伦准则，其摩擦角 φ和泊松比ν应满足式（3）［13－14］：

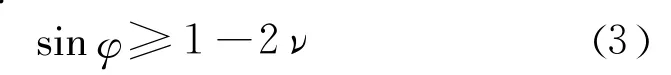
在强度参数折减的同时，为了保持式（3）的成立，从而引出假定关系式：

式中：φi和νi对应于强度折减系数Fi；β为常数。

式中：φ和ν为岩石的真实参数。

同时，假定弹性模量 Ei的变化规律符合下式定义［14］：

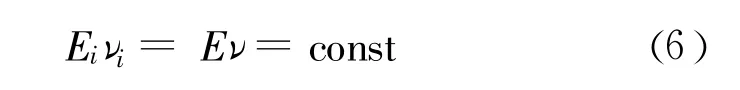
式中：E和ν为岩石的真实参数。

文献［13］通过理论和试验数据推导了坡体材料泊松比的折减方法，认为式（3）在土质边坡中是适用的，并应用于均质土坡的稳定性分析。因此本文的刚度参数的调整基于公式（3）和公式（6），具体方法如下［14］：

（1）先将岩石土体材料的实际强度参数，代入式（5），求得参数β；

（2）给定一个强度折减系数 Fi，由式（1）求出折减后的 ci、φi；

（3）由式（7），求得 Ei和νi；

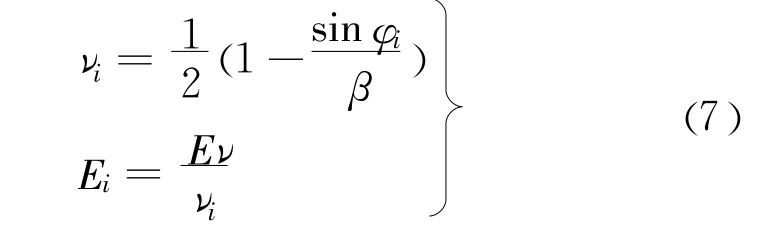
（4）以 ci、φi、Ei、νi为参数进行有限元分析；

（5）若计算已使得边坡达到临界极限状态，则取边坡安全系数 Fs＝Fi，并结束分析，否则需要重新选取一个新的强度折减系数 Fi重复（2）步。

1.5 研究思路

为了探讨刚度参数 E和ν的取值对边坡的安全系数是否有影响，分别在DP3和DP4准则下，计算出各坡比下不调整刚度参数取值的强度折减法（分别简称DP3、DP4）和调整了刚度参数取值的强度折减法（分别简称DP3′、DP4′）时的安全系数。同时，为了验证计算结果的准确性 ，又采用了符合实际的简化bishop法计算出来边坡的安全系数，并与在DP3、DP3′、DP4、DP4′下计算出来的安全系数进行对比。

2 有限元建模

本文采用大型通用有限元软件ANSYS12.0建立二维边坡模型进行分析。土体材料采用Plane82单元，按平面应变分析计算。边界范围的取值为坡顶到左侧竖向边界的距离为坡高的2.5倍，坡脚到右侧竖向边界的距离为坡高的1.5倍，并且上下边界高度为2倍坡高。同时网格的划分考虑合理的网格密度，模型的边界条件考虑为左右两侧法向约束，底部为固定约束，上部为自由边界。模型施加竖直方向的重力加速度为9.8m／s2。本文建立的有限元模型尺寸（未知尺寸根据坡比推出）如图1所示。网格划分及约束如图2所示。

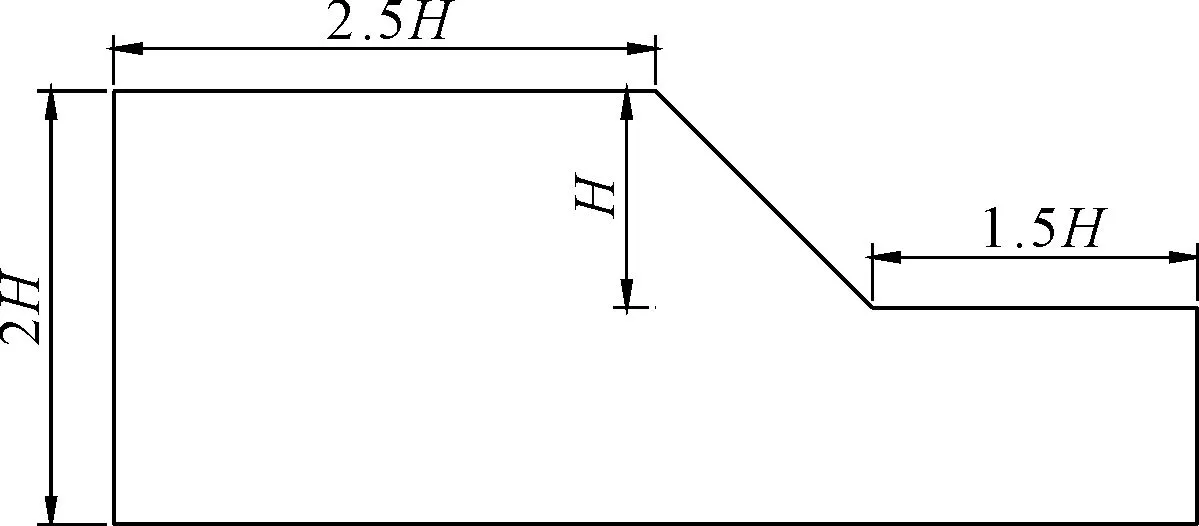
图1 模型尺寸示例

图2 有限元模型

3 算例及分析

均质土坡，坡高 H＝20 m，土重度 γ＝19 kN／m3，黏聚力с＝20 KPa，内摩擦角 φ＝25°，弹性模量 E＝20MPa，泊松比ν＝0.3。分别求出在坡比为1∶0.75，1∶1，1∶1.25，1∶1.5，1∶1.75，1∶2，1∶2.25，1∶2.5，1∶2.75，1∶3时的安全系数，简化Bishop法计算的边坡安全系数通过理正岩土软件实现。计算结果详见表2。

由表2的（DP1－B）／B一栏中计算结果比较，我们可以得出，用有限元强度折减法进行边坡稳定分析时，DP1准则的计算结果比简化Bishop法的计算结果平均要大26.4%左右，边坡的坡比越大，结果误差越大，且远远大于传统极限平衡方法（如简化Bishop法）的计算结果，因此采用DP1准则计算出来的结果误差偏大，计算结果用于工程实际分析偏于危险；DP3准则的计算结果比简化Bishop法的平均大4.5%左右，DP4准则的计算结果比简化Bishop法的平均小1.6%左右，这两者的计算精度均可满足工程需要，证实了有限元法用于工程的可行性。因此，在进行边坡稳定方面的有限元分析计算时有必要把DP1准则转换为DP3或者DP4准则。

DP3′与DP3的计算结果近乎相等，DP4′与DP4相比也是如此。因此，用有限元强度折减法分析计算边坡安全系数时，是否调整边坡土体刚度参数的取值，对计算边坡安全系数的结果影响非常小。建议在此类计算中可以假定弹性模型和泊松比是不变的，所带来的计算结果误差可以忽略不计。

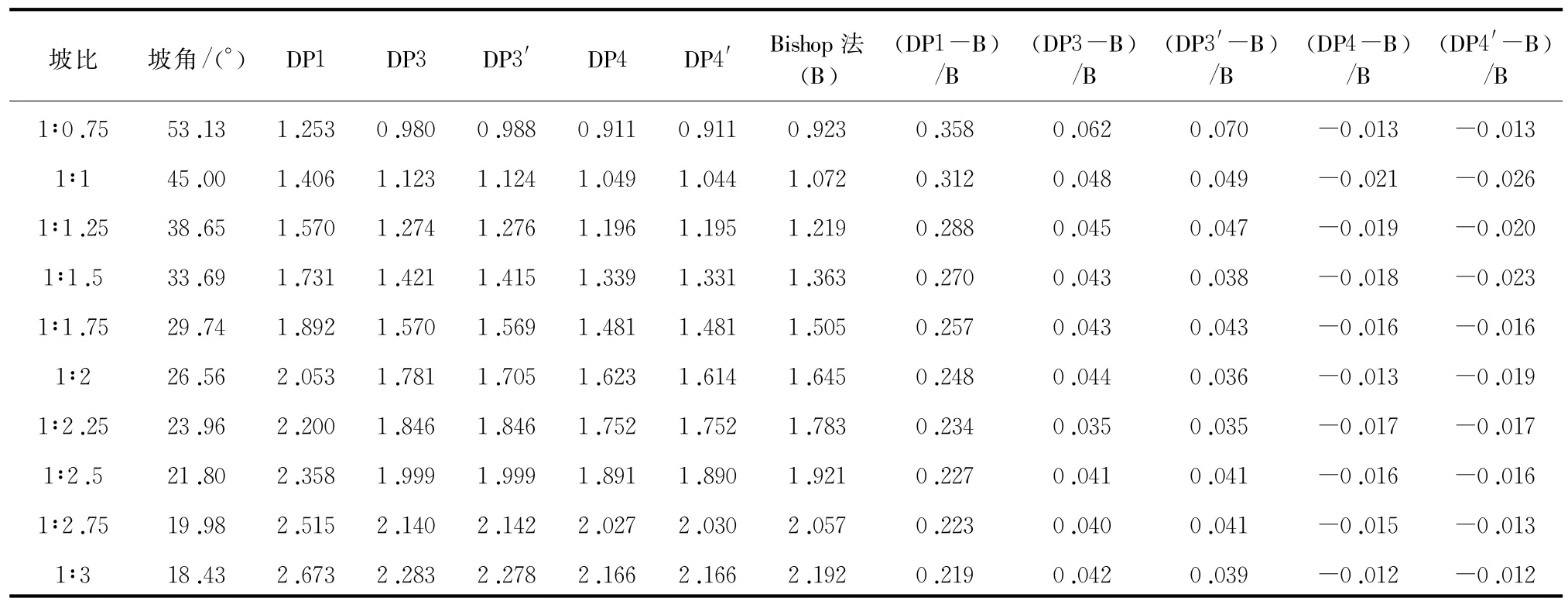
表2 边坡安全系数表

另外，在强度折减时，不采用 E、ν根据公式（7）同时调整的方法，在 E不变时ν变化或者E变化时ν不变这两种情况下来探讨E、ν各自取值变化对边坡有何影响及影响程度，取坡比为1∶1.5，折减系数为 Fi＝1.2时，使用DP4准则进行计算。

当泊松比ν＝0.3保持不变时，改变弹性模量 E的取值，从10MPa变化到20MPa，利用ANSYS的后处理功能，观察边坡等效塑性应变云图，如图3、图4所示，发现弹性模量 E的改变对坡体的塑性区的分布范围没有影响，但是对坡体的位移和变形是有显著影响的，弹性模量从10MPa变化到20MPa时，坡体的整体位移逐渐变小，如图5。

当弹性模量E＝20 MPa保持不变时，改变泊松比ν的取值，从0.25变化到0.35，利用ANSYS的后处理功能，观察边坡等效塑性应变云图，如图6、图7所示，可知泊松比取值的变化，对坡体的塑性区的分布范围的影响很明显，泊松比的取值越大，边坡的塑性区范围越小；同时随着泊松比的增大，边坡的总体位移逐渐减小，如图8。

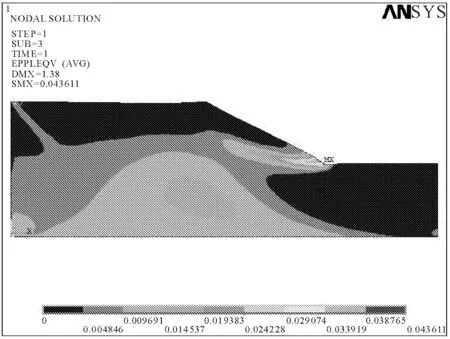
图3 等效塑性应变云图（E＝10MPa）

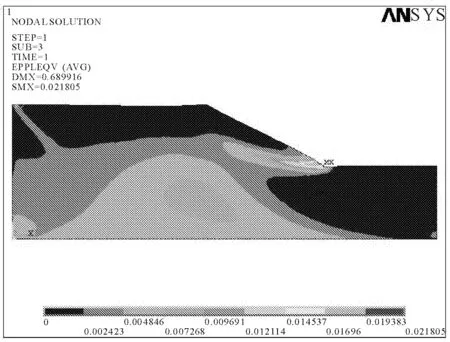
图4 等效塑性应变云图（E＝20MPa）

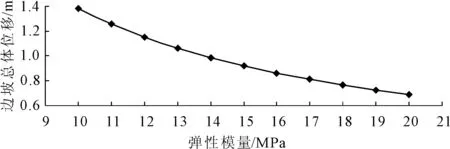
图5 边坡整体位移随弹性模量变化的曲线

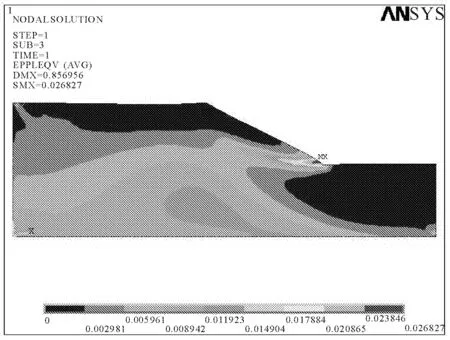
图6 等效塑性应变云图（ν＝0.25）

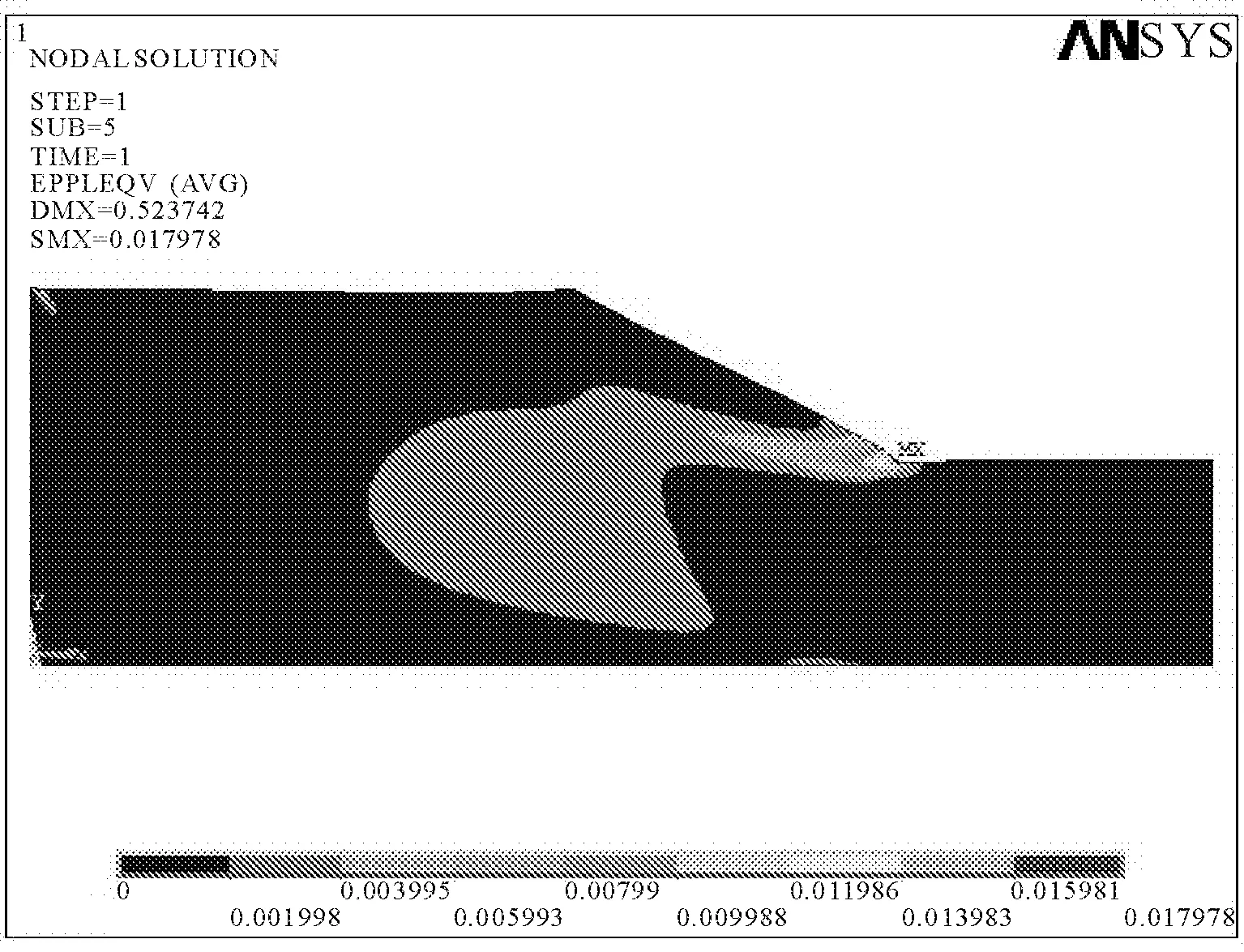
图7 等效塑性应变云图（ν＝0.35）

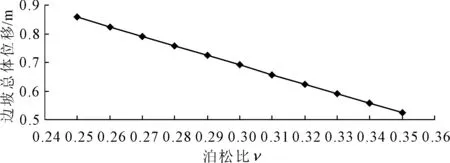
图8 边坡整体位移随泊松比变化的曲线

4 结 论

（1）使用有限元强度折减法进行边坡的稳定分析不仅可靠，而且与传统极限平衡法相比更为直观。在实际分析中应用DP3、DP4准则比DP1准则计算出来的误差要小，计算出来的安全系数可以直接用于边坡的稳定分析。

（2）在边坡稳定分析中，不需要考虑弹性模量和泊松比取值的变化，因为它们对边坡的安全系数计算结果影响微乎其微。在实际分析中，如果没有这方面数据，可以按照经验或者参照工程地区周边原有参数来选弹性模量和泊松比，即使选取有所不当，对稳定分析的结果也是影响很小的。

（3）粘聚力和内摩擦角是影响边坡安全系数的主要参数，而弹性模量和泊松比对边坡安全系数影响非常小。因此在实际边坡稳定分析时，粘聚力和内摩擦角取值应准确，切合实际情况。

（4）用强度折减法可以求出边坡的安全系数，在强度折减后计算出来的位移和变形的值并不反映实际的真实的位移和变形。但是可以通过这些变形和位移的变化趋势反映出刚度参数变化对边坡的变形和位移是有影响的。因此在边坡的变形分析中，必须准确的选取边坡的弹性模量与泊松比。

（5）泊松比不变时，弹性模量取值的变化对坡体的塑性区的分布范围没有影响；当弹性模量保持不变时，泊松比的取值越大，边坡的塑性区范围越小。

［1］ 戴自航，卢才金.边坡失稳机理的力学解释［J］.岩土工程学报，2006，28（10）：1191－1197.

［2］ 唐 芬，郑颖人.强度储备安全系数不同定义对稳定系数的影响［J］.土木建筑与环境工程，2009，31（3）：61－65，97.

［3］ 刘金龙，栾茂田，赵少飞，等.关于强度折减有限元方法中边坡失稳判据的讨论［J］.岩土力学，2005，26（8）：1345－1348.

［4］ 郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用［J］.岩石力学与工程学报，2003，23（19）：3381－3388.

［5］ 赵尚毅，郑颖人，张玉芳.极限分析有限元法讲座－Ⅱ有限元强度折减法中边坡失稳的判据探讨［J］.岩土力学，2005，26（2）：332－336.

［6］ 吕 庆，孙红月 ，尚岳全 .强度折减有限元法中边坡失稳判据的研究［J］.浙江大学学报（工学版），2008，42（1）：83－87.

［7］ 唐 芬，郑颖人.边坡渐进破坏双折减系数法的机理分析［J］.地下空间与工程学报，2008，4（3）：436－442.

［8］ 张鲁渝，时卫民 ，郑颖人 .平面应变条件下土坡稳定有限元分析［J］.岩土工程学报，2002，24（4）：487－490.

［9］ 柳林超，梁 波，刁 吉 .基于ANSYS的有限元强度折减法求边坡安全系数［J］.重庆交通大学学报：自然科学版，2009，28（5）：899－901.

［10］ 秦 帆，王正中.基于有限元强度折减理论的边坡稳定分析方法探讨与改进［J］.水利与建筑工程学报，2012，10（1）：43－47.

［11］ 连镇营，韩国城，孔宪京.强度折减有限元法研究开挖边坡的稳定性［J］.岩土工程学报，2001，23（4）：407－411.

［12］ 钱家欢，殷宗泽.土工原理与计算（第2版）［M］.北京：中国水利水电出版社，1996.

［13］ 张培文，陈祖煜.弹性模量和泊松比对边坡稳定安全系数的影响［J］.岩土力学，2006，27（2）：299－304.

［14］ 郑 宏，李春光，李焯芬，等.求解安全系数的有限元法［J］.岩土工程学报，2002，24（5）：626－628.

［15］ 赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24（3）：343－346.

Study on the Value of Elastic Modulus and Poisson’s Ratio of Slope Stability Calculation of Strength Reduction Method

PAN Xin－en
（School of River and Ocean Engineering，Chongqing Jiaotong University，Chongqing 400074，China）

To explore the impactof elasticmodulus and Poisson’s ratio on the stability parameters by adapting strength reductionmethod ，the stability of the slope coefficient was calculated，using the finite element strength reduction method.While the strength parameterswere reduced，the elasticmodulus and Poisson’s ratiowere adjusted according to the formula.The slope stability coefficient drawn from thatwas compared with the ones obtained by keeping the elastic modulus and Poisson’s ratio unchanged.It is found that adjusting the value of the elasticmodulus and Poisson’s ratio had little impact on slope stability coefficient.The result suggests that only the strength parameters of reduction needs considering when calculating the stability parameters by using the finite elementstrength reductionmethod.It isunnecessary to consider the changes of elasticmodulus and Poisson’s ratio.

slope stability analysis；safety factor；strength reduction；elasticmodulus；Poisson’s ratio

TU441＋.35

A

1672—1144（2014）04—0055—05

10.3969／j.issn.1672－1144.2014.04.010

2014－02－21

2014－03－25

水利水运工程教育部重点实验室开放基金（SLK2009B01）；重庆市国土资源和房屋管理局科技项目资助

潘新恩（1989—），男（壮族），广西南宁人 ，硕士研究生 ，研究方向为水利工程灾害形成机理及防治。