双向水平循环荷载下单桩承载力的离心模型实验
2014-07-07王忠涛赵守正
张 宇,王忠涛,赵守正
(1.大连理工大学海岸和近海工程国家重点实验室 ,辽宁大连116024;2.大连理工大学土木工程学院岩土工程研究所,辽宁大连116024;
3.中交四航工程研究院有限公司,广东广州510000)
双向水平循环荷载下单桩承载力的离心模型实验
张 宇1,2,王忠涛1,2,赵守正3
(1.大连理工大学海岸和近海工程国家重点实验室 ,辽宁大连116024;2.大连理工大学土木工程学院岩土工程研究所,辽宁大连116024;
3.中交四航工程研究院有限公司,广东广州510000)
针对饱和密砂地基,采用位移控制方式,分别进行了单向水平位移和双向水平循环位移加载下刚性单桩基础的离心模型实验。实验表明:桩端反力随位移荷载循环次数的增加而增加,10次循环后,桩端反力逐渐趋于稳定;桩身弯矩与桩端反力基本呈线性变化 ,最大弯矩出现在1/3埋深附近;随着水平位移和循环次数的增加,桩体转动中心最终稳定在2/3埋深附近。
单桩;水平荷载;双向循环;离心模型实验;位移控制
作为建筑、港口、近海钻井平台和海上风机等工程结构物的常用基础形式,桩基础往往同时承受着较大的竖向荷载、水平荷载和弯矩的作用。水平荷载下的桩-土相互作用较为复杂,针对这类问题,国内外学者开展了大量模型实验研究,文松霖等[1]通过离心模型实验探讨了加载位置对桩基础水平承载力的影响;Verdure[2]、Li等[3]和Klinkvort等[4]对水平循环荷载下密砂中桩-土相互作用问题进行了离心模型实验研究,讨论了荷载-位移曲线的割线刚度随循环荷载次数的变化规律,以及由循环荷载引起的永久变形的累积规律,并发现砂土中桩的极限承载力并未因循环荷载的作用而减小;王富强等[5]采用臂式离心模型实验探讨了饱和砂土中桩基础在水平循环荷载下的受力变形规律。但上述模型实验均采用应力控制加载,或仅考虑单向水平循环荷载。为讨论不同位移幅值的循环荷载作用下,单桩基础承载力的变化规律,本文采用位移控制法,针对单向水平位移和双向水平循环位移加载下的单桩进行了离心模型实验,分析了桩身的响应规律,包括双向水平循环位移加载对单桩基础临界承载力的影响、桩身弯矩的分布规律、以及桩体的转动中心变化规律等。
1 实验设备
1.1 土工鼓式离心机
实验采用国内首台大型土工鼓式离心机GT450/1.4,环形模型槽直径为1.4 m,深度为0.27 m,宽度为0.35m。设备负载能力450 g・t,最大离心加速度600 g,此时对应的最大载重为0.75 t。其性能优良,功能全面,在机械设备规模、数据采集精度、控制系统自动化程度及作动器加载模式方面均领先于国外同类产品。
1.2 砂土成样装置
砂土地基成样采用自主研发的自动撒砂装置,以严格控制试样的相对密实度和均匀性,确保实验的高度可重复性,设备如图1所示。撒砂筒上部装有孔径可调的薄片,以控制砂土的流量,下部装有双层滤网,确保出砂的均匀性。撒砂筒在伺服电机驱动控制下,可实现精确的三维运动,包括水平向、竖向的移动速度和行走路线均可严格控制,保证撒砂过程中落距始终相同。整套设备适用于制备相对密实度范围为0.47~0.94的均匀砂样。实验中为获得相对密实度为0.92的密砂,参照赵守正等[6]和曾虹静等[7]的经验图表,选用6mm孔径的喷嘴薄片,落距为400mm,撒砂筒水平移动速度为50mm/s,每次同水平面撒砂循环后提高撒砂筒15mm。

图1 自动撒砂装置和撒砂筒示意图
1.3 加载装置
实验中选用自主研发的Maxon伺服电机驱动加载装置。装置固定于离心机中轴的作动器上,如图2所示。最大加载行程200mm,加载速度可精确控制在0.001mm/s~0.5mm/s。本实验采用位移式控制加载,桩端水平向加载速度为0.05 mm/s。通过图2中的连接部件6,可实现加载装置与桩头光滑接触,有效避免了加载过程中机械摩擦引起的桩体上拔。

图2 实验加载装置及测量系统设计图(单位:mm)
1.4 测量系统
实验中采用非接触式激光位移传感器Laser测量桩身位移,通过测力杆获得桩端反力,布置方式如图2。激光位移传感器布置在砂面上方,其中Laser1距砂面19 mm,Laser2距砂面75 mm。实验中以Laser1采集的水平位移作为加载的控制参数。测力杆双侧贴有应变片,经过严格标定可测算桩端受力。桩身布置4组高精度应变片以测算桩身弯矩,敷设位置距地基表面依次为17mm、42mm、67mm和92 mm。
2 实验方案
2.1 实验模型
实验中使用弹性模量约为65 000MPa的高强度硬铝合金空心圆管模拟刚性桩,尺寸为,外径 d=20 mm,壁厚 t=2mm,长L=200mm,埋深h=100mm。实验在50 g离心加速度下进行,模型比尺为1∶50,相对应的原型钢桩尺寸为桩径 d=1m,壁厚 t=0.1 m,桩长L=10m,埋深 h=5m。
实验模型箱由铝合金制成,长度 a=310mm,宽度 b=290mm,深度 c=180mm,底部铺有中砂并覆盖透水板,可通过底部进水阀缓慢注水饱和砂样。由于 b/d=14.5>5[8],可忽略模型边界效应的影响。
2.2 地基材料
地基材料选用福建标准砂,筛除大于0.5mm粒径的砂粒后,粒径特征参数列入表1。砂土颗粒级配曲线如图3。因为 d/d50=20/0.17=117.6>30[1],可忽略颗粒效应的影响。

表1 砂土基本参数

图3 土料颗粒级配曲线
2.3 实验步骤
第1步:在1 g条件下,用自动撒砂装置制备相对密实度为0.92的砂样,通过模型箱侧壁底部的进水阀缓慢注入无气水饱和砂样。
第2步:砂样饱和完成后,在1 g条件下通过伺服电机作动器,以0.05 mm/s的速度将桩垂直压入模型箱的中心位置,贯入深度为100mm。
第3步:桩安装完毕后,通过模型箱下方的进水阀排出砂样中的部分水分,使砂样能够侧立。安装传感器,并将模型箱固定在离心机环形模型槽内,准备实验。
第4步:开始离心模型实验,先将离心机提速至20 g,在此条件下向环形模型槽内通水,直至自由水面超出砂面。将离心机提速到50 g,待水面平稳、且传感器信号稳定后进行加载,完成实验。
2.4 实验内容
通过4组离心模型实验,分别考虑单向加载和双向循环加载以及循环位移幅值的变化,分析和讨论了水平荷载下密实砂土地基中刚性桩的响应规律。各组实验工况列入表2。
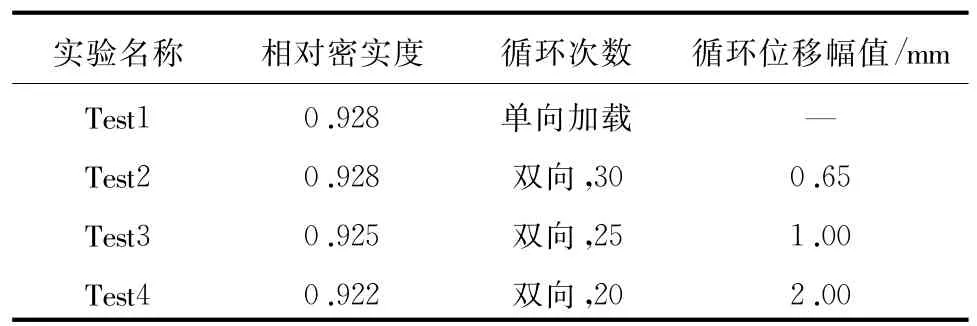
表2 实验工况
Test1为单向水平位移加载,最大加载位移为7 mm;Test2~Test4分别按照水平位移控制进行双向循环加载,循环位移幅值A依次为0.65 mm、1 mm和2mm。循环加载实验中,当位移幅值处的桩端反力趋于稳定时停止加载,以确定循环加载次数,对应次数列于表2。为考察循环位移加载后的单桩承载能力,在Test2~Test4循环加载结束后,分别进行一次单向位移加载,当桩端反力趋于稳定时停止加载,对应的水平位移依次为6.5mm、6.0mm和5.0mm。
3 实验结果分析
3.1 单向水平位移加载下桩端反力
图4(a)为4组实验中第1轮循环达到加载位移幅值前,桩端反力 H和水平位移u的关系曲线,4条曲线趋势相同,相同水平位移范围内曲线基本重合,总体上桩端反力随位移增加而增大。可以看出 H-u曲线的第1个拐点出现在0.2mm水平位移处,对应临界承载力 Hcr=25 N,第2拐点不明显,后期呈非线性变化。

图4 循环加载前后单向加载 H-u曲线
3组循环加载实验结束后,继续进行1次单向水平位移加载实验,相应的 H-u曲线见图4(b)。经过循环位移加载后,对应原起始位置桩端反力不为0,为便于比较,图中曲线均以桩端反力为0时,即完全卸载后作为新起始点,相应位置如图4(b)所示。桩周砂土在刚性桩的挤压下,表面有少许隆起,桩周土体形成椭圆形凹陷,凹陷深度小于桩埋深3%。总体上桩周砂土受刚性桩挤压变得更为密实,桩承载力得以提高,因此3条曲线初始斜率相比图4(a)均有明显增大,水平临界荷载 Hcr明显增大,均超过100 N。但达到临界荷载 Hcr所需的位移也明显增大,基本接近循环加载的位移幅值,同时注意到,之前经历的双向循环加载位移幅值越大,桩端反力在相同的水平位移处越小,即 H-u曲线的初始斜率越低。原因是桩周凹陷区域和深度随循环位移增大而增大,对桩的承载能力发挥有一定影响。出现临界荷载后,随着循环位移的继续发展,桩端反力继续增大,但增长率逐渐减小,最终趋于稳定。
3.2 循环位移加载下桩端反力
图5为按位移控制的双向水平循环荷载下桩端反力H和水平位移u的滞回曲线,图6为对应各循环中最大桩端反力及其增长率与循环次数的关系曲线。

图5 循环加载 H-u曲线
由图5~图6可知,对应循环位移幅值处,桩端反力随循环次数的增加而增加。首次循环时桩端反力的增量最大,3组实验中反力增量分别为18.7%, 16.4%和14.1%。当循环次数达到10次以后,桩端反力增长速率开始减缓,每次循环的增量不超过3%。循环加载结束后,Test2、Test3、Test4中桩端反力的增长率分别达到85%、79%和51%,说明循环位移幅值A越大,桩端反力的增长率越小。

图6 最大桩端反力及其增长率与循环次数的关系
3.3 水平荷载下桩身弯矩
图7为单向位移加载实验中桩身弯矩与桩端反力的对应关系,可以看出两者基本呈线性关系。由于实验采用的是位移控制法,注意到图4(a)中桩端反力与水平位移为曲线变化关系,结合桩身截面的弯矩计算公式,可知桩侧土体的刚度系数为非线性变化,与桩端反力随水平位移的变化规律一致。因此当采用位移法控制施工时,以往假定地基比例系数m为恒值是不准确的。

图7 桩身弯矩与桩端反力的关系
图8是随循环次数变化对应位移幅值时桩身弯矩沿深度的分布规律。由图8可以看出3组实验中弯矩分布趋势基本相同,随着循环次数增加,桩身弯矩有一定增长。前10次的循环中,桩身弯矩增长较为明显,随着循环次数的增多,增幅逐渐变小,达到20次循环后,桩身弯矩趋于稳定。3组实验中,距地基表面17mm和42mm位置处弯矩基本相同,说明最大弯矩出现在2个位置区间内,与王富强等[5]得出的位于1/3埋深位置处的结论相近。靠近桩底位置,弯矩接近0,说明小尺寸刚性桩的桩底竖向地基抗力很小,未引起有效弯矩,符合理论解。

图8 桩身弯矩随深度的变化
3.4 水平荷载下桩体转动中心
实验桩的模型材料为高强度铝合金管,可忽略自身变形,根据Laser1和Laser2量测的不同位置的水平位移,可计算出桩的转动中心。实验结果表明桩体转动中心随桩身水平位移的变化而改变,循环加载次数对桩体转动中心的位置影响较小。
以单向加载为例,加载过程中桩体转动中心随加载位移的增加而上升,如图9所示。实验初始阶段,转动中心约在砂面以下75mm处,随后较快上升到距砂面65mm左右,随着水平位移进一步增加,转动中心缓慢上升最终稳定在砂面以下60mm左右。类似地,循环加载实验最初的3个循环,桩体的转动中心从砂面以下75mm左右上升到65 mm左右,并最终稳定在65mm左右。综合4组实验来看,转动中心最终稳定在2/3埋深附近。
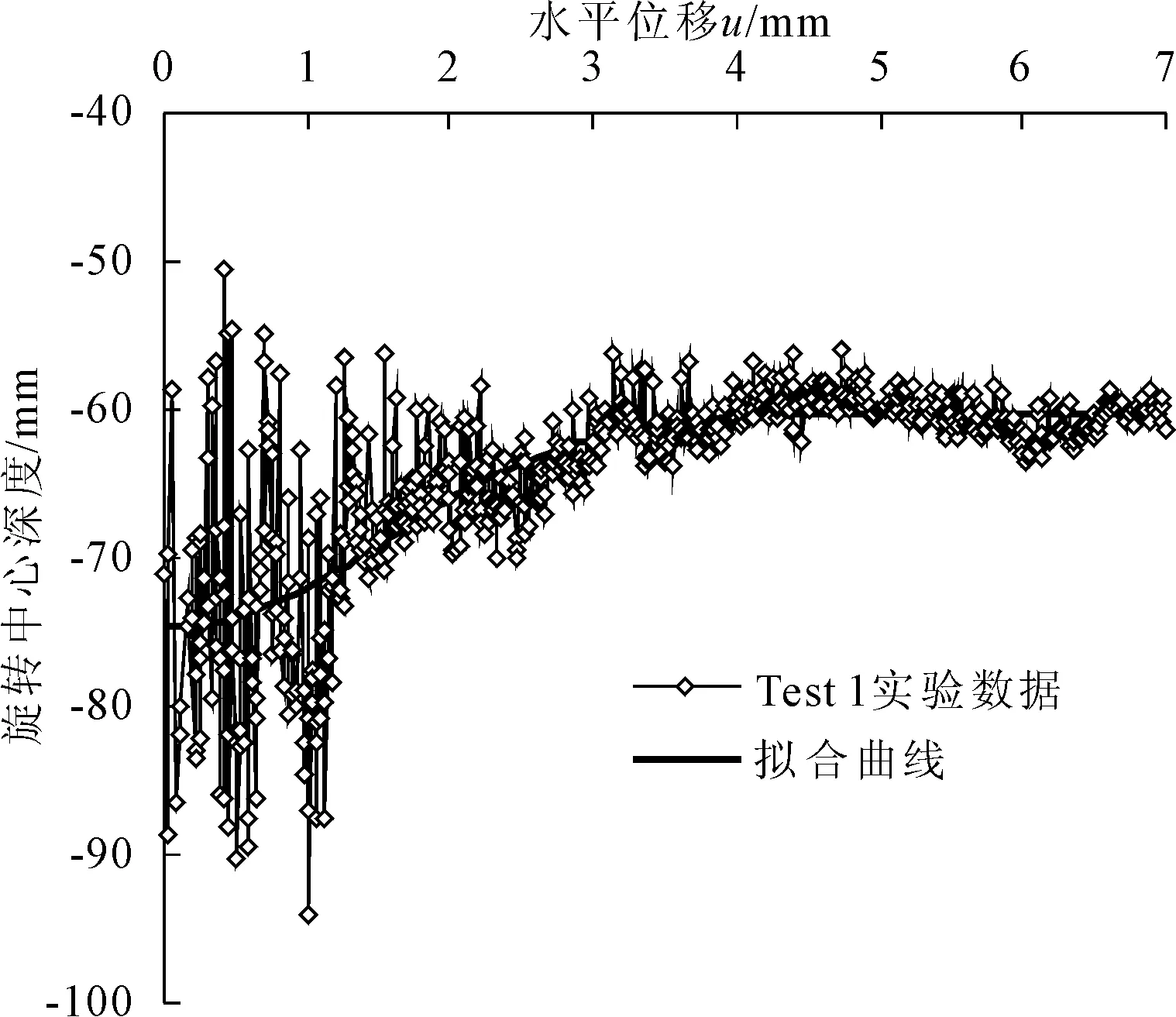
图9 桩体转动中心的变化
4 结 论
通过单向水平位移和双向水平循环位移加载刚性单桩的离心模型实验,分析得出如下结论:
(1)循环加载后,桩的水平承载能力有所提高,但受桩周砂土凹陷深度和范围的影响,循环位移幅值越大,达到临界荷载所需的位移越大,桩端反力随水平位移的增长斜率越低。
(2)循环加载实验中,对应循环位移幅值,桩端反力随循环次数的增加而增加,循环次数10次后,桩端反力转为缓慢增长,并逐步趋于稳定。循环位移幅值越大,桩端反力增长率越小。
(3)桩身弯矩与桩端反力基本呈线性变化,桩侧土体的刚度系数为非线性变化,与桩端反力随水平位移的变化规律一致;最大弯矩出现在1/3埋深的附近。靠近桩底位置,弯矩接近0。
(4)随着水平位移和循环次数的增加,刚性桩的转动中心会有上升,最终稳定在2/3埋深附近。循环次数对转动中心的位置影响不大。
[1] 文松霖,柴红涛.加载高度对桩基水平承载特性影响的离心模型试验研究[J].岩土工程学报,2011,33(S2):69-73.
[2] Verdure L,Garnier J,Levacher D.Lateral cyclic loading of single piles in sand[J].International Journal of Physical Modeling in Geotechnical,2003,3(3):17-28.
[3] LiZ,Haigh SK,BoltonM D.Centrifugemodellingofmonopile under cyclic lateral loads[C]//7th International Conference on Physical Modelling in Geotechnics,Zurich,2010:965-970.
[4] Klinkvort RT,Leth CT,HededalO.Centrifugemodeling of a laterally cyclic loaded pile[C]//7th International Conference on PhysicalModelling in Geotechnics,2010:959-964.
[5] 王富强,荣 冰,张 嘎,等 .水平循环荷载下风电机桩基础离心模型试验研究[J].岩土力学,2011,32(7):1926-1930.
[6] 赵守正,栾茂田 ,王忠涛,等 .自动撒砂装置的研制与测试[J].水利与建筑工程学报,2013,11(5):176-182.
[7] 曾虹静,王忠涛 ,罗 强,等 .自制砂土装样设备及其控制要素分析[J].人民长江,2012,43(11):66-70.
[8] Ovesen NK.The use of physicalmodels in design:the scaling law relationships[C]//Proceedings of 7th European Conference on Soil Mechanics and Foundation Engineering.Brighton,1979:318-323.
Centrifugal Tests of Single Pile’s Bearing Capacity Subjected to Bidirectional Cyclic Lateral Loading
ZHANG Yu1,2,WANG Zhong-tao1,2,ZHAO Shou-zheng3
(1.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian,Liaoning 116024,China;2.Institute ofGeotechnical Engineering,School of Civil Engineering,Dalian University of Technology,Dalian,Liaoning 116024,China;3.CCCC Fourth Harbor Engineering Institute Co.,Ltd.,Guangzhou,Guangdong 510000,China)
Centrifugemodel tests forsingle pileburied in saturated dense sandwere carried out to investigate the behavior of pile foundation subjected to unidirectional and bidirectional cyclic lateral displacement loadings separately.The results indicate that the reaction force riseswith cycles of lateral displacement loading,and it becomes stable after 10 cycles gradually.The bendingmoment varieswith the reaction force linearly,and the biggestmoment’s position is at around 1/3 buried depth.With the increasing of lateral displacementand cycles,the rotation center stables ataround 2/3 buried depth.
single pile;lateral loading;bidirectional cyclic loading;centrifugal test;displacement control
TU449
A
1672—1144(2014)04—0027—05
10.3969/j.issn.1672-1144.2014.04.005
2014-04-08
2014-05-10
国家自然科学基金项目(50909014,51079018),国家重大科技专项“南海深水油气开发示范工程”子课题“南海北部陆坡区地质灾害风险评价预测研究”(2011ZX05056-001-02),中央高校基本科研业务费专项资金资助(DUT14ZD220)
张 宇(1987—),男 ,辽宁阜新人 ,硕士研究生 ,研究方向为近海结构物的承载特性研究。
