随机波浪作用下海底管线与海床的相互作用研究

邓海峰，王忠涛，刘 鹏

（1.大连理工大学海岸和近海工程国家重点实验室 ，辽宁大连116024；2.大连理工大学土木工程学院岩土工程研究所，辽宁大连116024）

随机波浪作用下海底管线与海床的相互作用研究

邓海峰1，2，王忠涛1，2，刘 鹏1，2

（1.大连理工大学海岸和近海工程国家重点实验室 ，辽宁大连116024；2.大连理工大学土木工程学院岩土工程研究所，辽宁大连116024）

针对随机波浪作用下海底管线的动力响应是设计中需考虑的重要因素，考虑波浪随机特性、管－土接触和惯性效应，建立了二维有限元管－土相互作用的数值计算模型，开展了摩擦系数、埋深、管径、海床渗透系数对管周孔隙水压力、管线竖向位移及其内部正应力影响的数值模拟研究。研究成果可为海底管线设计提供技术参考。

随机波浪；海底管线；相互作用；接触效应；惯性效应

作为由海上油气田向陆地输送石油和天然气的工程结构物，海底管线得到了广泛应用。波浪荷载是海底管线设计中需要考虑的主要因素之一。在天然波浪作用下海底管线的受力形式非常复杂，其中涉及到管线、波浪和土体的相互作用。波浪在海面传播过程中引起的波压力将会通过海床土体的渗透性进一步传递到海床土体内部，对海床内部的有效应力和孔隙水压力分布有显著影响，海床土体的孔隙水压力逐渐累积，同时有效应力逐渐减小，最终导致海床将会出现液化或者滑移等失稳破坏现象，进而引起海底管线的上浮或者下沉［1］。综上，为了能够正确合理地估计海底埋置管线在波浪作用下的工作状态，就一定要掌握海底管线在波浪作用下的动力响应以及管线周边海床的受力状态。

MacPherson［2］采用解析方法求解了无限深度海床中海底埋置管线的波浪渗流力大小；McDougal［3］利用映像法对此问题也得到了相应的解析解答；Lennon［4］采用边界积分方法对波浪作用下海底管线周边海床土体的孔隙水压力分布进行了研究。但上述所有研究中均包含了以下假定：孔隙流体不能够被压缩、土骨架不可变形，同时孔隙水压力满足Laplace方程。因此其结果与实际差距较大。

基于Biot固结理论［5］，相关学者对海底管线在波浪作用下海床土体内部的孔隙水压力做了大量的数值研究。Cheng［6］和Magda［7］采用边界积分方法计算得到了管线周边海床土体内部的孔隙水压力分布情况。但上述几种方法均假定海底管线为刚性体，同时仅对管线周边的孔隙水压力与管线受到的上升力进行了计算分析，而没有考虑海底管线的内部应力。栾茂田［8－9］利用有限单元法对海床－管线在非线性波浪作用下的相互作用进行了系统研究；刘靖［10］针对管－土接触摩擦效应对海底管线在规则波浪作用下的动力响应进行分析。但是自然条件下的波浪具有明显的不规则特性，所以根据非线性和线性波浪基本理论发展起来的相应计算方法，不能够合理地反映海底管线的动力响应。为此，Kumar［11］和Neelamani［12］分别通过室内模型试验进行了相关研究。王忠涛［13］应用有限元方法，结合随机波浪谱分析，同时基于Biot动力固结理论对自由海床在随机波浪荷载作用下的动力响应进行了系统分析。远航［14］采用随机波浪谱分析方法，进行了黄河口埕岛油田管土相互作用的有限元数值分析，但未考虑海底埋置管线的内部应力分布。

本文假定海底管线为线弹性材料，考虑管－土惯性效应及其接触摩擦效应，同时结合随机波浪谱分析，建立了随机波浪作用下管线－海床相互作用二维有限元模型，进而对管线和海床的动力响应进行了系统分析。对惯性效应以及管－土接触摩擦效应对随机波浪作用下海底管线的动力响应的影响进行了重点分析，并分析了不同管－土接触摩擦系数、管线埋深、半径和海床土体的渗透系数对随机波浪作用下管线内部正应力及其位移和管线周边孔隙水压力的影响。

1 基本理论

考虑有限深度海床厚度为 s，海底管线埋置在海床内部一定深度内 ，管线半径为 R，埋深为 b，海床底面不透水且为刚性。波浪沿着水平方向传播，z坐标自不透水刚性基底起向上，如图1所示。

图1 波浪 －管 －土相互作用示意图

1.1 控制方程

根据Biot动力固结理论［5］，海床内部孔隙介质的质量守恒方程为：

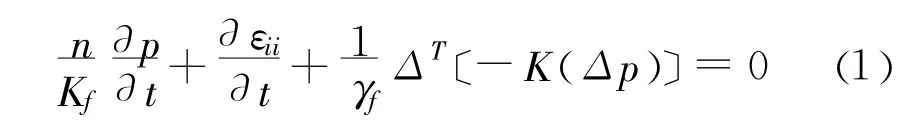
式中：K为海床土体渗透系数，p为孔隙水压力，εii为海床土体体积应变，Kf为海床内部孔隙流体体变模量，γf为海床内部孔隙流体重度，n为土体的孔隙率。

根据Luan［9］可知，当忽略土体骨架和孔隙流体的相对加速度时，海床土体的动平衡方程为：

式中：δij为Kronecker符号，为土体加速度为土体的有效应力，bsi和ρs分别为土体体积加速度与密度。

按照弹性动力学理论，埋置管线的控制方程为：

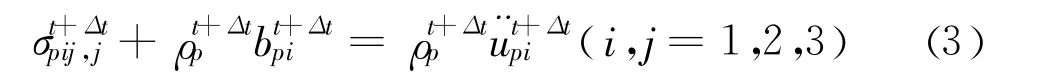
式中：ρp为管线密度，σpij为管线内部应力，为管线加速度，bpi为管线体积加速度。

1.2 边界条件

不透水刚性海床底面：

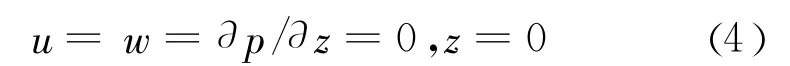
式中：u、w分别为海床土体水平和竖向位移。海床表面位置处的波浪压力和孔隙水压力相等，可以表示为：

式中：P为海床表面波浪压力，pb为孔隙水压力，γw为海水的重度，ai、ki、fi、εi分别为第i个线性规则波浪的波高、波数、频率和初始波相角。

假设管线为刚性不透水材料，因此其表面的孔隙水压力梯度可表示为：

式中：n表示管线外表面法线方向。

1.3 接触问题

在波浪荷载作用下，管线与海床在其接触面上可能发生相互错动，所以要在接触位置设置相应的接触单元。本文在考虑接触效应时采用约束函数的接触算法，同时分别选择管线和土体为主、从接触面，两接触面构成接触对［15］。根据Coulomb摩擦理论，管线－海床之间的摩擦力为τ＝μpc，式中，μ为接触摩擦系数大小；pc为接触压力大小。当管土之间的拖曳力小于摩擦力时，管土间不会出现相对滑移现象。

2 有限元模型

数值模型长度取120m，海床厚度取40m，尺寸远大于最大管线半径，以避免边界效应，如图2所示。考虑到管线周围的应力集中，在管线及其附近采用了局部网格加密，通过选取特定点进行网格检验，得到可用于计算的最小网格密度。当考虑管－土接触时，确定沿管线环向和径向分别划分80份和10份，同时与管线外表面相接触的海床土体的网格划分密度与其保持一致，管线采用八节点四边形单元，海床土体采用四节点四边形单元［9］，如图3所示。根据刘靖［10］的研究成果可知，管线半径、埋深和土体渗透系数对海底管线动力响应具有显著影响 ，本文基于Luan［9］和刘靖［10］综合制定管线和管周土体的物理参数，详见表1。

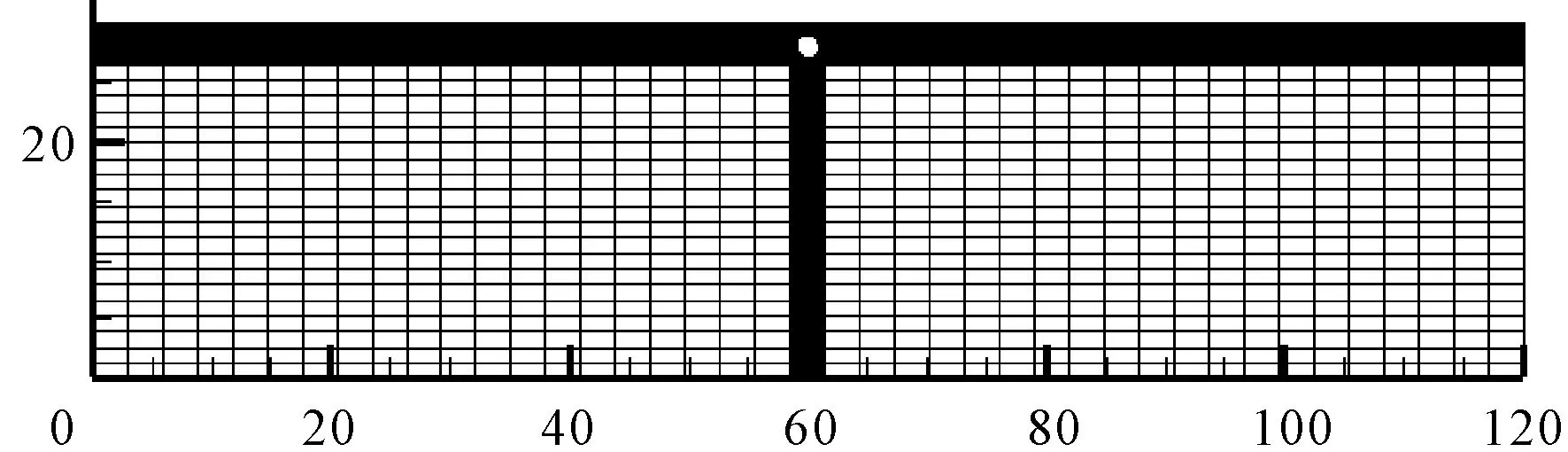
图2 有限元模型示意图

图3 管周土体网格剖分

表1 管线和管周围土体的物理参数

3 随机波浪时程序列模拟

本文采用线性波浪叠加方法［16］模拟随机波浪的时程序列。选用平均JONSWAP谱作为模拟谱，其谱密度函数为：

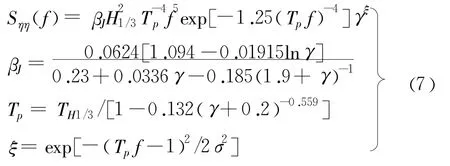
式中：Tp＝1／fp，fp为频谱峰值点对应的频率，βJ为用于调整谱面积的参数 ，H1／3和 TH1／3为前1／3部分线性规则波的平均值，γ＝3.3，为谱峰增强因子。当f＞fp时，σ＝0.07，反之σ＝0.09。设定99.8%的波能量集中在低频fL＝0和高频fH＝5 fp之间，因此设定 Δf＝ Δfi＝（fH－fL）／M。

模拟波浪的参数 H1／3＝6m，TH1／3＝15 s，水深d＝25m，模拟得到的随机波浪时程序列时间大于30倍的代表性波浪周期，如图4所示。

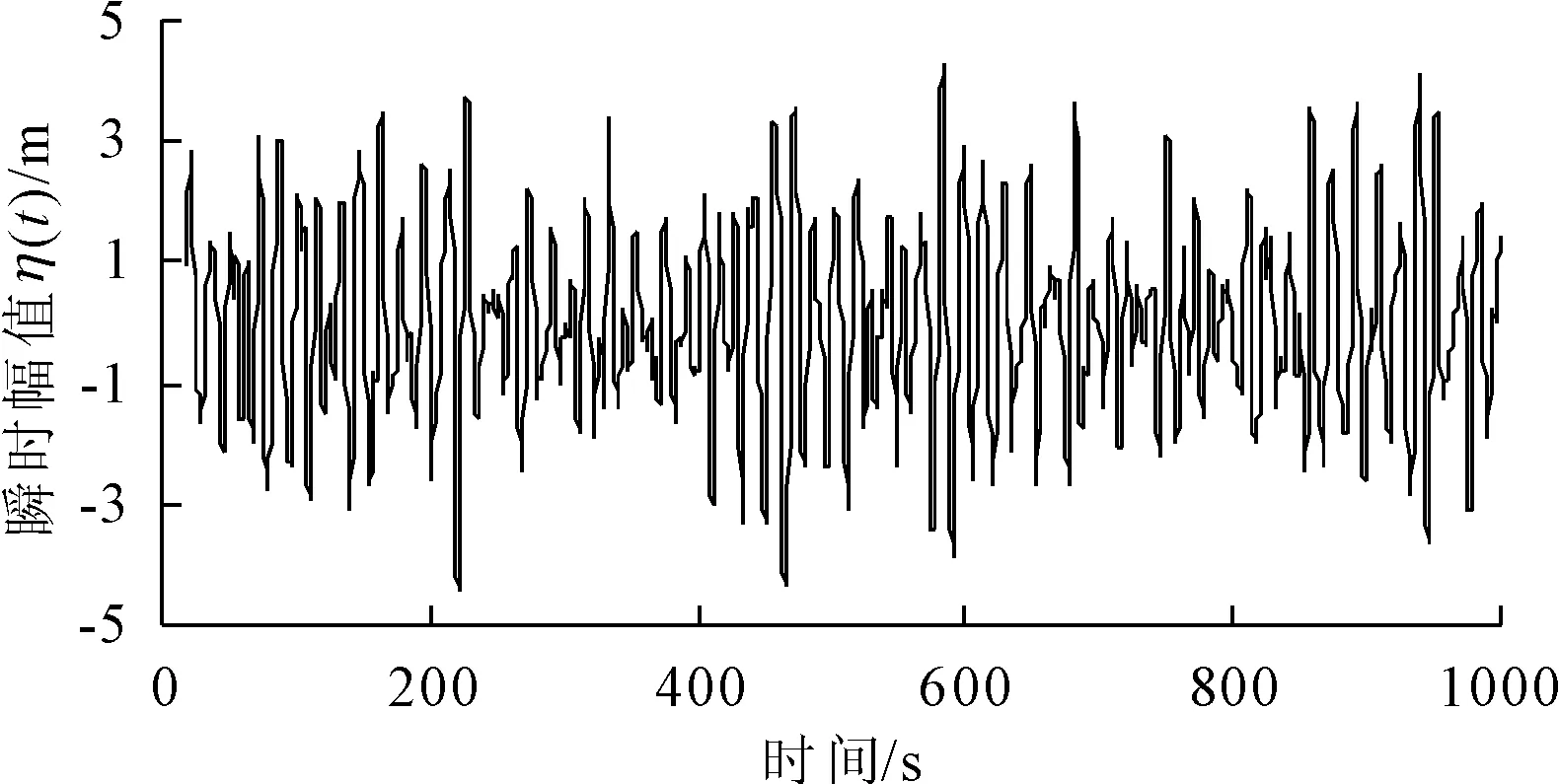
图4 模拟的随机波浪时程序列

根据自相关函数反推出模拟得到的随机波浪时程序列的模拟谱，并对其光滑处理，可看出靶谱和平滑谱二者很好地拟合，如图5所示。因此根据线性波浪叠加法模拟得到的随机波浪时程序列可用于本文的求解。

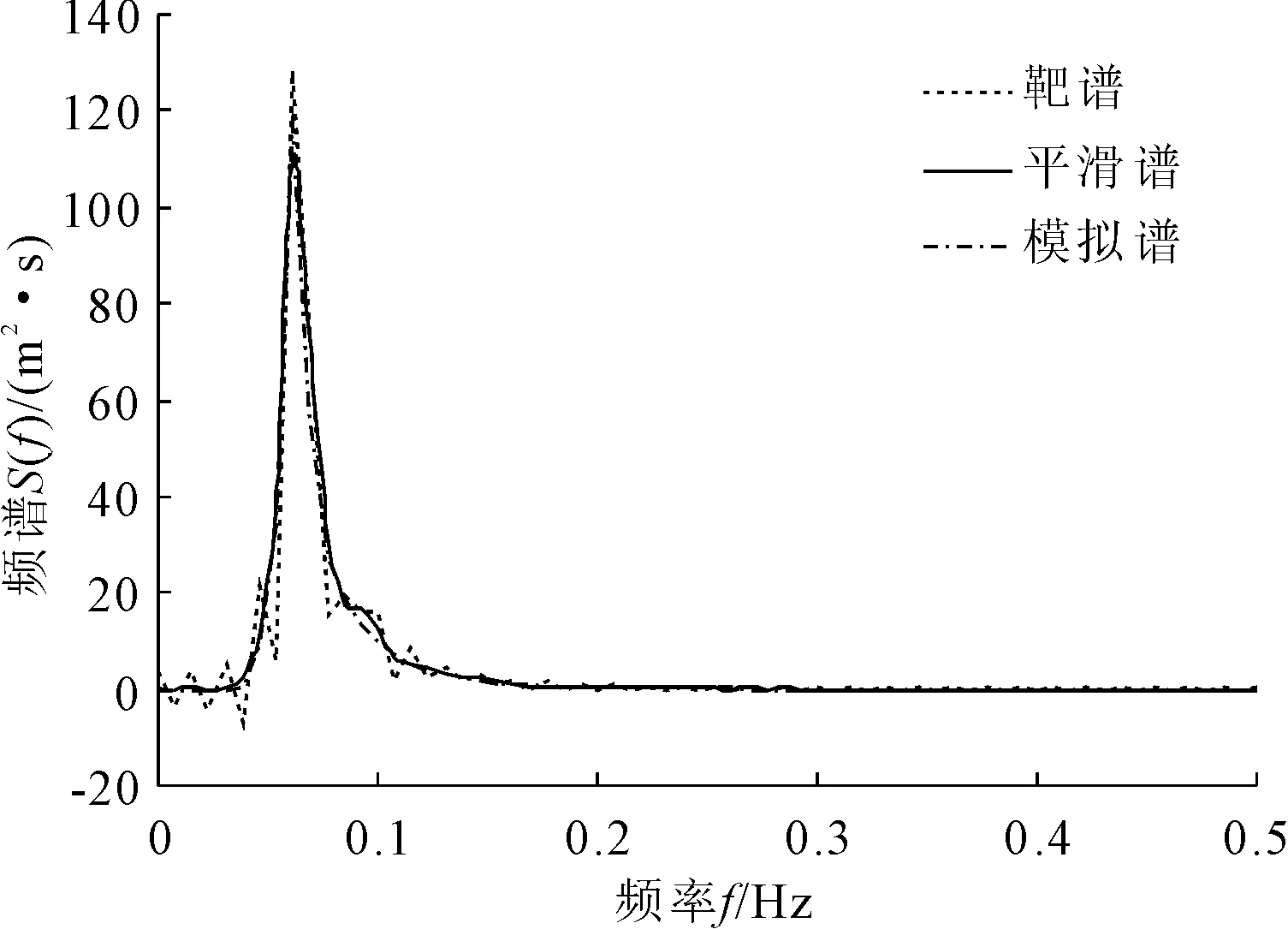
图5 模拟生成谱、平滑谱和靶谱的比较

4 数值计算与对比分析

4.1 管－土接触效应的影响

在管线埋深b＝1m、管线半径 r＝1m，分别针对考虑和忽略管－土之间的接触效应（μ＝0.4）两种情况，图6给出随机波浪作用下管线内部正应力及其位移和管线周围孔隙水压力的分布情况。由图6可以看出，接触摩擦效应对随机波浪作用下管线内部正应力影响显著，但对管线周围孔隙水压力的影响特别小。同时根据图6（b）、图6（c）可知，忽略接触摩擦效应会显著低估管线内部正应力。如图6（d）所示，考虑管－土接触效应时，管线正上方处管线和土体的竖向位移时程存在一定差异，表明考虑接触效应时，管线受土体约束作用减弱，管－土将发生相对运动，管线稳定性降低。因此，在海底管线的设计中必须考虑管－土相互作用。

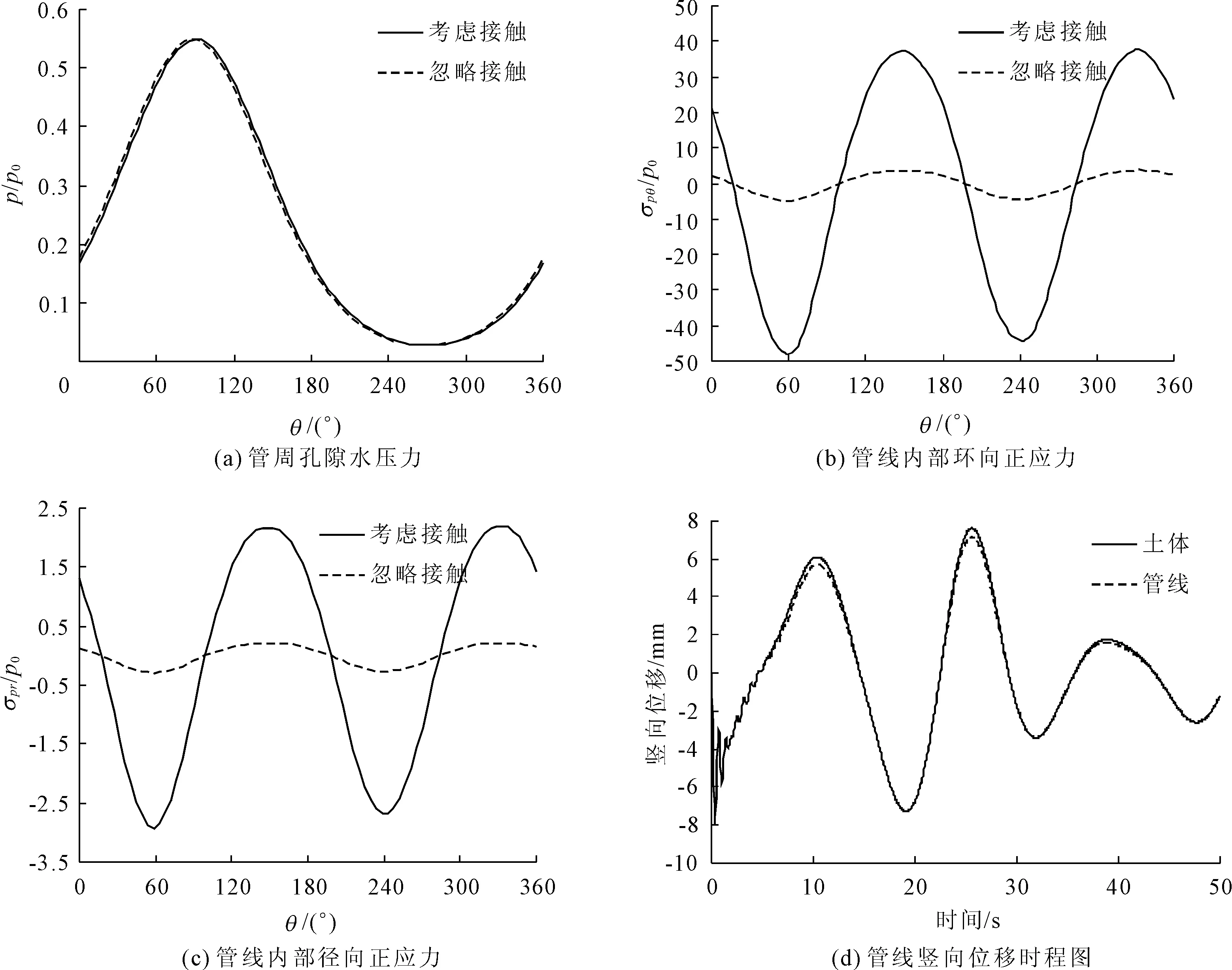
图6 接触效应对管周土体孔隙水压力、管壁内部正应力及管线竖向位移的影响

4.2 摩擦系数的影响

不同工况条件下管－土间接触摩擦系数差异显著。本文拟选取摩擦系数 μ为0.2、0.4、0.6，同时考虑管线半径和埋深均为1m。图7给出了不同摩擦系数条件下管线内部正应力及其位移和管线周边孔隙水压力的分布情况。由图7可以看出，摩擦系数的变化对管线内部正应力及其位移具有显著影响，同时可以看出，管线内部正应力及其位移随管－土间摩擦系数增大而逐渐减小；但摩擦系数对管线周围孔隙水压力的分布影响很小。工程上通常采用向管沟填充粗粒料来增加管－土间的摩擦力，进而满足海底管线的竖向稳定及结构安全。

4.3 惯性效应的影响

在管线埋深b＝1m、管线半径 r＝1m条件下，分别考虑和忽略惯性效应两种工况，图8给出了随机波浪作用下管线周边土体孔隙水压力、管线外表面环向正应力、径向正应力及管线位移分布。由图8可见，管－土惯性效应随机波浪作用下管线内部正应力及其位移和管线周围孔隙水压力基本没有影响。综上可以得出本文所选工况条件下，管线和海床土体控制方程中的加速度项可以忽略。

4.4 管线埋深及管径的影响

如前所述，管－土间的惯性效应和接触效应对随机波浪作用下管线内部正应力及其竖向位移的影响显著，同时考虑管－土惯性效应和接触摩擦效应计算得到的管线内正应力及管线位移与同时忽略两种效应计算得到的结果差值也会受到管线几何尺寸及埋深的影响。

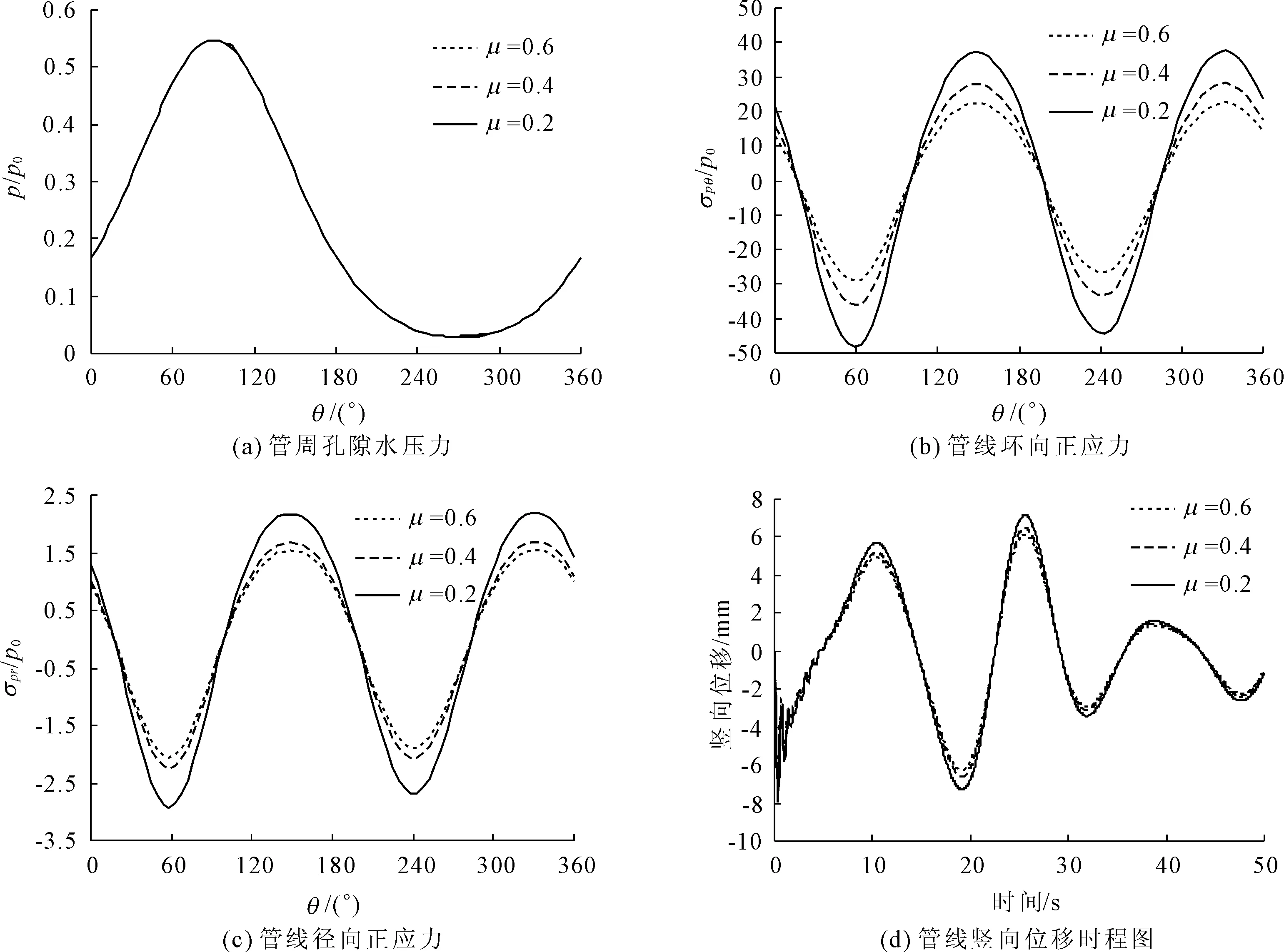
图7 不同摩擦系数下的管周孔隙水压力、管线内部正应力及管线竖向位移比较

图8 管－土惯性效应对管周土体孔隙水压力、管线内部正应力及管线竖向位移的影响

图9给出了不同管线埋深 b和管径r下，同时考虑或同时忽略两种效应时计算得到的管线竖向位移差值 ΔVp、环向正应力差值 Δσpθ和径向正应力差值Δσpr，其中μ＝0.4。由图9可以看出，管线埋深和半径对管线竖向位移及正应力差值影响显著，竖向位移差值随管线半径的增加而增大，随管线埋深的增加而减小；随管线埋深和半径的增加，管线内部正应力差值减小。结果表明，在管线浅埋或管线半径较小的情况下，必须考虑管－土相互作用。

图9 管线几何尺寸对管线竖向位移差值和环向、径向正应力差值的影响

4.5 海床土体渗透系数的影响

作为海洋土中极其重要的参数，渗透系数对随机波浪作用下海底管线的动力响应具有显著影响。

数值计算工况同上节，分别更改海床土体渗透系数 kz为1×10－3m／s（工况1）和1×10－5m／s（工况2），同时考虑管－土接触及惯性效应计算管线竖向位移和内部正应力的比值，结果如图10所示。Vc、σθc、σrc和Vf、σθf、σrf分别为工况1和工况2中管线的竖向位移、环向正应力和径向正应力。由图10可知 ，Vc／Vf位于7～30之间，σθc／σθf和 σrc／σrf位于2.5～10之间，表明埋置在渗透系数较大的土中的管线位移及正应力明显大于渗透系数小的土。同时可以看出，当管线半径 r减小，埋深 b增加时，管线竖向位移受渗透系数影响更大 ；而渗透系数对管线内部正应力的影响随管线埋深和半径的增加而增大。

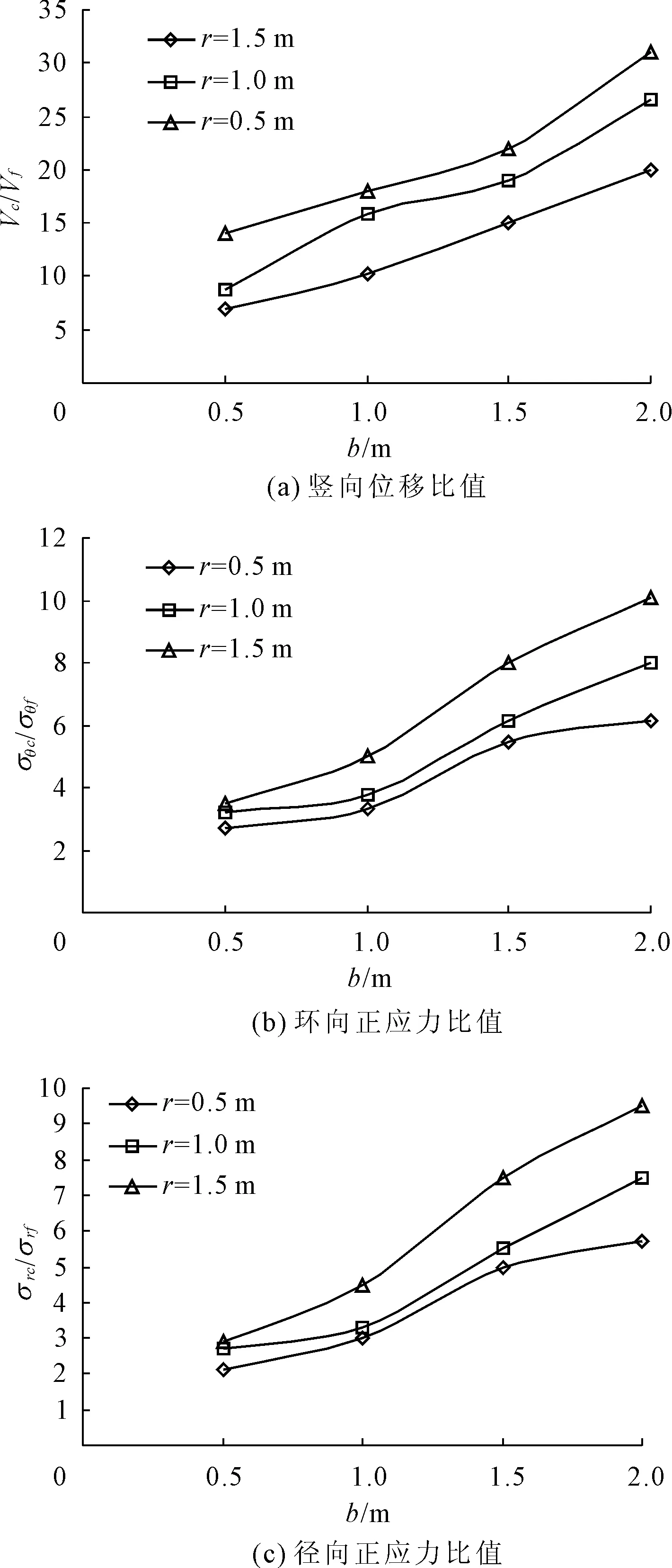
图10 管线几何尺寸对管线竖向位移比值和环向、径向正应力比值的影响

5 结 论

通过以上分析，可以得出如下结论：

（1）管－土间接触摩擦对随机波浪作用下管线内部正应力影响显著，但对管线周围孔隙水压力的影响特别小，忽略接触效应会显著低估管线内部正应力。惯性效应对海床及管线的动力响应影响较小 。

（2）管－土间接触摩擦系数管线内部正应力及其位移影响显著，同时随摩擦系数增大而逐渐减小，但对管线周围孔隙水压力的分布影响特别小。

（3）管线埋深和半径对同时考虑或忽略接触及惯性效应计算得到的管线竖向位移差值和管线内部正应力差值均有显著影响。管线竖向位移差值随管线半径的增加而增大，随管线埋深的增加而减小；管线内部正应力差值随管线埋深和半径的增加而减小 。

（4）相比渗透系数小的土，在渗透系数较大的土中计算得到的管线竖向位移及正应力明显增大。同时可以看出当管线半径 r减小，埋深 b增加时，管线竖向位移受渗透系数影响更大；而渗透系数对管线内部正应力的影响随管线埋深和半径的增加而增大。

［1］ Sumer B M，Fredsoe J，Christensen S，et al.Sinking／Floatation of pipelines and other objects in liquefied soil underwaves［J］.Coastal Engineering，1999，38（2）：53－90.

［2］ MacPherson H.Wave forces on pipeline buried in permeable seabed［J］.Journalof theWaterway PortCoastal and Ocean Division，1978，104（4）：407－419.

［3］ McDough W G，Davidson S H，Monkmeyer P L，et al.Wave－induced forceson buried pipelines［J］.JournalofWaterway，Port，Coastal and Ocean Engineering，1988，114（2）：220－236.

［4］ Lennon G P.Wave－induced forces on buried pipelines［J］.Journal ofWaterway，Port，Coastal and Ocean Engineering，1985，111（3）：511－524.

［5］ BiotM A.General theory of three－dimensional consolidation［J］.Journal of Applied Physics，1941，12（2）：155－164.

［6］ Cheng A HD，Liu PLF.Seepage forceon a pipeline buried in a poroelastic seabed underwave loading［J］.Applied O－cean Research，1986，8（1）：22－32.

［7］ MagdaW.Wave－induced uplift force on a submarine pipeline buried in a compressible Seabed［J］.Ocean Engineering，1997，24（6）：551－576.

［8］ 栾茂田，曲 鹏，杨 庆，等.非线性波浪作用下海底管线—海床动力响应分析［J］.岩土力学，2007，28（6）：709－714.

［9］ Luan M T，Qu P，Jeng D S，et al.Dynamic response of a porous seabed－pipeline interaction underwave loading：Soilpipeline contact effects and intertial effects［J］.Computers and Geotechnics，2008，35（2）：173－186.

［10］ 刘 靖，李明高.海底管道与多孔弹性海床的相互作用研究［J］.水电能源科学 ，2009，27（5）：159－163.

［11］ Neelamani S，Narasimha Rao S.Wave interaction with a submarine pipeline in clayey soil due to random waves［J］.Ocean Engineering，2005，32（13）：1517－1538.

［12］ Neelamani S，Al－Banaa K.Wave force variation due to burial of submarine pipeline in random wave fields［J］.International Journal of Earth Sciences and Engineering，2011，4（4）：601－613.

［13］ 王忠涛，栾茂田，Jeng D S，等.随机波浪作用下海床动力响应及液化的理论分析［J］.岩土力学，2008，29（8）：2051－2057.

［14］ 远 航，贾永刚，刘 涛.随机波浪作用下黄河口海床与管线相互作用数值模拟［C］／／城市地质环境与可持续发展论坛论文集.上海，2010：674－679.

［15］ 曲 鹏，栾茂田，郭 莹 ，等.波浪作用下饱和海床管线动力相互作用的有限元分析［C］／／第七届全国土动力学学术会议论文集，北京：清华大学出版社，2006：446－453.

［16］ 俞聿修.随机波浪及其工程应用［M］.大连：大连理工大学出版社，2000.

Study on Seabed－Pipeline Interaction under Random Wave Loading

DENG Hai－feng1，2，WANG Zhong－tao1，2，LIU Peng1，2
（1.State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China；2.Institute ofGeotechnical Engineering，School of Civil Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China）

It is a key issue to define the dynamic response of buried submarine pipeline subjected to random wave loading in the design of submarine pipelines.Taking the stochastic behavior ofwaves，contact and inertia effects into consideration，a2－D finite elementanalysismodelwasestablished considering pipeline－soil interaction，based onwhich，the influence factors including frictional coefficient，buried depth，pipe radius and permeability of seabedwere analyzed to study the impacts on pore pressure，vertical displacement and normal stress of the pipes respectively.The derived conclusion provides a technical support for the design of submarine pipelines.

random wave；submarine pipeline；interaction；contact effects；inertia effects

TU449

A

1672—1144（2014）04—0043—07

10.3969／j.issn.1672－1144.2014.04.008

2014－03－17

2014－04－07

国家自然科学基金项目（51079018，50909014）；国家重大科技专项“南海深水油气开发示范工程”子课题“南海北部陆坡区地质灾害风险评价预测研究”（2011ZX05056－001－02）；高等学校博士学科点专项科研基金资助课题（20120041130002）

邓海峰（1989—），男 ，吉林舒兰人 ，硕士研究生 ，研究方向为随机波浪作用下海底管线动力响应。