方管中中性悬浮颗粒惯性迁移现象的数值研究*
2014-07-05姚同林余钊圣邵雪明
姚同林,余钊圣,邵雪明
(浙江大学力学系,浙江 杭州 310027)
0 引 言
颗粒悬浮流在自然界和工农业生产中广泛存在,如流化床、管道输运、细胞分离,以及更为常见的河道中泥沙沉降和输运等。尽管学术界对这种流动已有了大量的实验、数值方面的研究,但由于颗粒与流体之间相互作用的复杂性,至今对其流动特性以及作用机理仍缺乏足够的认识。
其中,Poiseuille流动中的粒子迁移问题是一个研究热点。该问题起源于 Segré and Silberberg[1-2]在1961年观测到的中性悬浮圆形颗粒在圆管中迁移到一个平衡位置,该平衡位置大约距离圆管中心轴有0.6倍的管半径的距离。之后,更多的学者(如Jeffrey[3],Karnis[4],Matas[5-6]等)通过更多深入的实验研究确认了Segré—Silberberg效应。最近,Matas等在 Re高于2400(基于管直径和平均速度)的实验中,发现了更靠近中心轴的平衡位置,称之为内环。在粒子迁移问题的数值模拟中,J.Feng等[7]研究了单个圆形粒子在二维 Poiseuille 流动中的运动。Pan & Glowinski[8-9]在平板和圆管Poiseuille流动下模拟了中性悬浮粒子的运动。Yu等[10]在垂直管 Poiseuille流动中模拟了中性悬浮和非中性悬浮球形颗粒的径向迁移速度、角速度及轴向速度。Shao等[11]在较大Re下,对圆管中球形颗粒的运动进行了模拟,验证了内部平衡点的存在。Chun&Ladd[12]研究了球形颗粒在方管中的迁移现象,模拟出了颗粒的两种平衡位置,并提出将两个粒子用弹簧捆绑在一起形成哑铃结构,新的平衡位置则会偏向方管中心。
综上所述,文献中对于圆管颗粒问题研究比较多,但对于方管中颗粒的惯性迁移问题模拟工作比较少,更缺乏对形成的两种不同平衡位置的研究。
本研究采用虚拟区域方法,研究中性悬浮球形颗粒在上下前后边界均为固定壁面的方管Poiseuille流中的惯性迁移问题。本研究主要关注雷诺数为100~1500范围内,颗粒粒径对惯性迁移现象的影响。本研究算法中对湍流和颗粒的模拟均使用直接数值模拟,没有引入模型,所以称为完全直接数值模拟。所采用的虚拟区域方法基于非贴体网格,在计算过程中无需移动和重新划分网格,简单高效且精度高。但对于网格大小以及时间步长有比较高的要求,而且计算量大。
1 数值方法
1.1 物理模型
一个颗粒在方管中的简单示意图如图1所示,其中z表示方管的流向,球形颗粒的半径为a;方管边长为2H;方管长度为L。在数值模拟中,颗粒与流体密度比ρr=1,即在方管内球形粒子处于中性悬浮状态。为减少计算区域,流向采用周期性边界条件,从右边界流出的颗粒与流体,再次以相同条件从左边界进入计算区域,如此循环,即可代表无限长的管道;x,y方向均采用壁面无滑移边界条件。
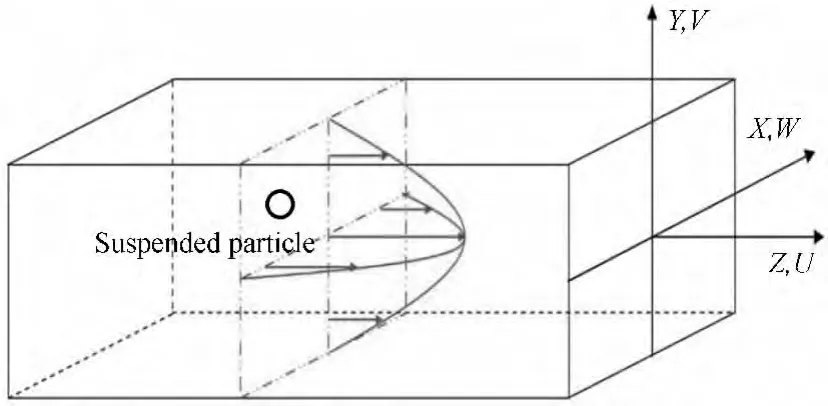
图1 方管中一个颗粒的示意图
本研究中将方管边长的一半(H)和流向中心线速度(um)作为特征长度和特征速度,以此定义的雷诺数为Rem=umH/ν。由于流向采用周期性边界条件,需要额外的压力梯度▽p=-dp/dz克服壁面摩擦力,以维持流动。方管进口速度剖面为方管Poiseille流动速度剖面:
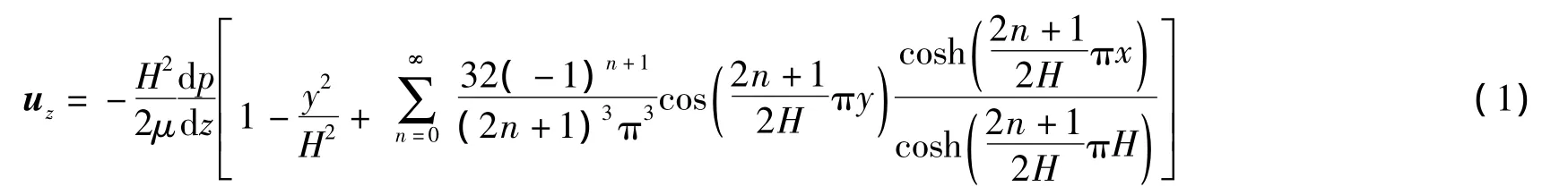
对处于平衡态的方管中的流体,无量纲后的额外压力梯度为:

1.2 虚拟区域法
本研究采用的模拟方法是由Glowinski等人[13]提出、余钊圣[14]推广改进的基于非贴体网格的直接力/虚拟区域法(DF/FD)。该方法的核心思想是假设固体颗粒内部充满流体,通过在这部分流体上引入虚拟体积力,使其符合刚体颗粒的运动。基于上述假设,虚拟区域法很好地处理了流体跟固体颗粒之间的界面问题以及两者之间的相互作用问题,在槽流和管流中得到了广泛应用,其有效性和正确性得到了充分的证明。
基于虚拟区域法的假定,本研究在颗粒内部引入虚拟体积力λ,假设颗粒的密度、体积、转动惯量、速度和角速度分别为 ρs,Vp,J,U 和 ωp,采用下述特征量来无量纲化控制方程:特征长度Lc,特征速度Uc,特征时间Lc/Uc,特征密度 ρf,特征压力,特征拟体力。
无量纲化之后的控制方程为:
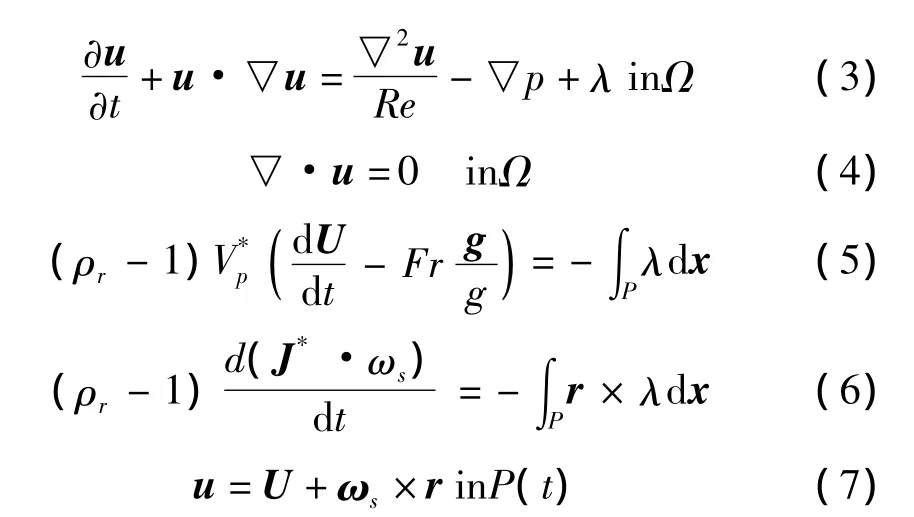
式中:Ω—整个计算区域;P(t)—颗粒占据的区域;Ωf—流体区域,Ωf=ΩP(t);r—以颗粒中心为原点的位置矢径。
无量纲化控制参数如下:
密度比:ρr= ρs/ρf;
雷诺数:Re= ρfUcLc/μ;
通过时间分裂步格式离散上述控制方程,将原来流固耦合的问题式(3~7)分解成流体子问题和颗粒子问题。其中流体子问题是一个标准N-S方程的求解问题,利用基于半交错风格的有限差分法和投影格式来求解,对于压力泊松方程采用基于快速傅里叶变换技巧快速求解。对于空间离散,全部采用基于半交错网格的二阶精度有限差分格式。颗粒问题的求解与DLM/FD方法不同,不需要迭代求解。
另外,本研究利用区域分解和MPI实现算法的并行化。在并行算法中,速度方程和压力方程均采用多重网格法(MG)进行迭代求解,有效保证了算法求解的速度与精度。
2 颗粒的惯性迁移分析
本节主要研究Re在100~1500之间,颗粒粒径对颗粒在方管中的惯性迁移平衡位置的影响,分别计算了管长为2H条件下,颗粒尺寸a/H=0.15、a/H=0.1和a/H=0.075这3种工况,划分的网格使得颗粒直径上有10个节点,单个颗粒算例的具体参数如表1所示。每种工况下,笔者选取约20种具有代表性的颗粒的初始位置,具体布置如图(2~5)所示。
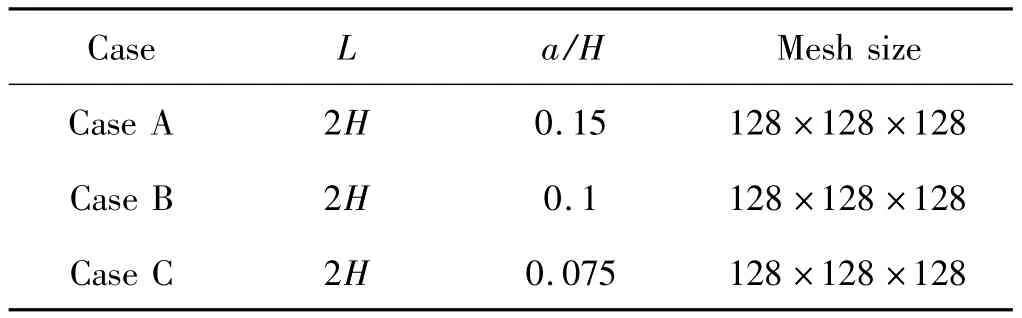
表1 单个颗粒算例的具体参数
以a/H=0.15为例,图(2~5)显示了颗粒迁移轨迹,方管中颗粒的平衡位置有两种:一种位于对角线上靠近角落;另一种位于边线中部,在整个方管中存在8个平衡点。两种平衡位置与壁面之间的距离有着明显的区别,在Re数(如图2、图3所示)较小时,二者与壁面间距离相差不多,随着Re数的增大,边线中部的平衡位置明显远离壁面,而Chun&Ladd采用格子玻尔兹曼方法模拟的结果显示,两个平衡位置总是距壁面0.2H。
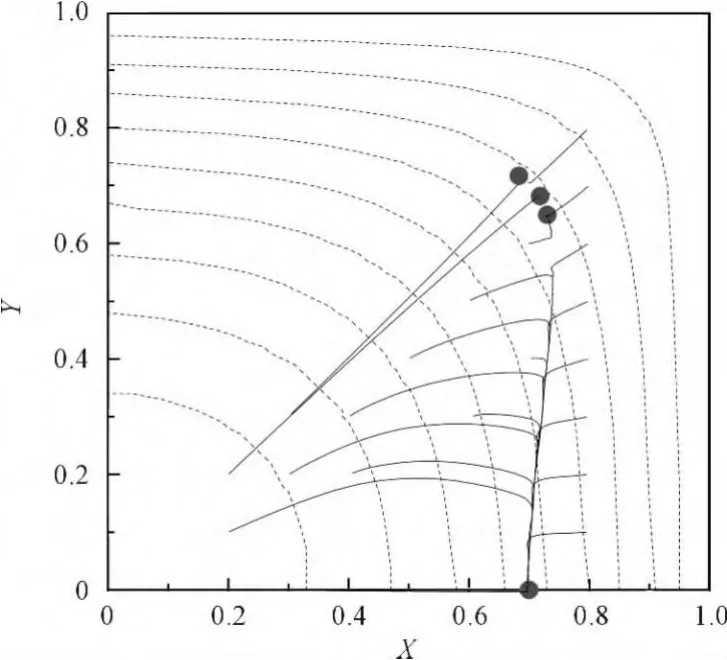
图2 Re=200下颗粒迁移轨迹在流向速度等值上的投影
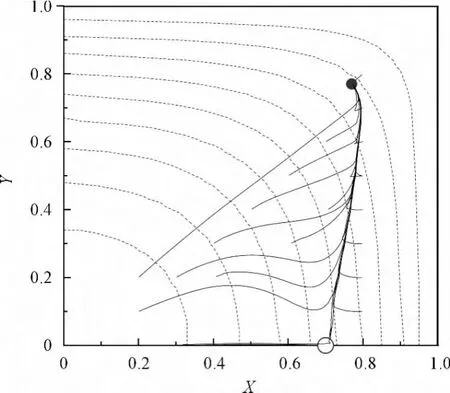
图3 Re=500下颗粒迁移轨迹在流向速度等值上的投影
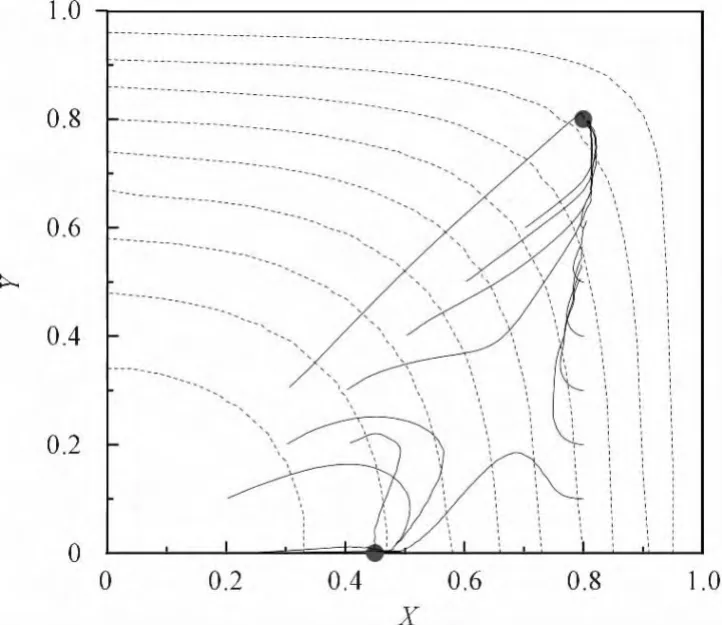
图4 Re=1000下颗粒迁移轨迹在流向速度等值上的投影
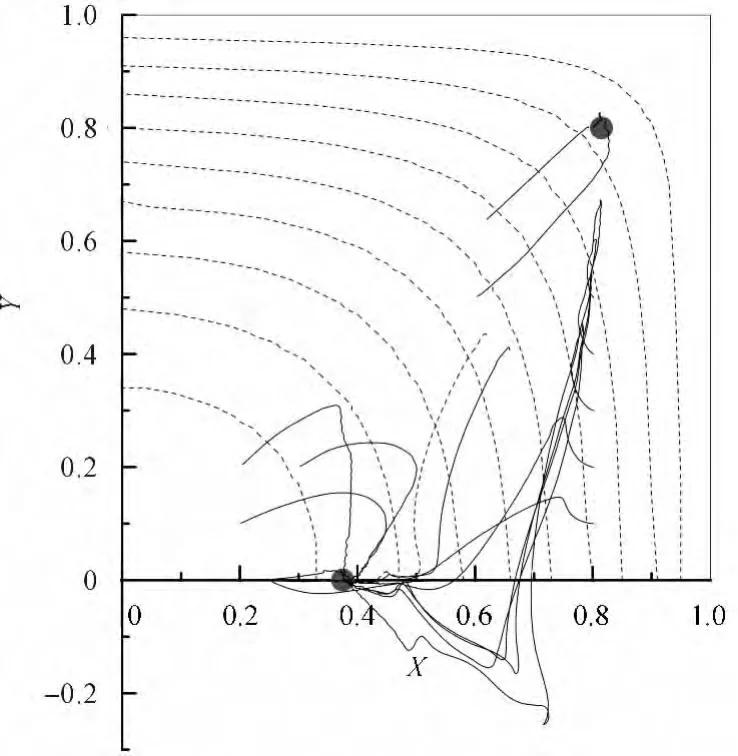
图5 Re=1500下颗粒迁移轨迹在流向速度等值上的投影
a/H=0.15条件下,方管、圆管和槽道迁移平衡位置的比较如图6所示。方管和圆管中的颗粒平衡位置相近,与槽道则明显不同。颗粒的迁移,如前所述,源于固壁施加给颗粒的力与速度梯度产生的力之间的不平衡,而方管与圆管在两个方向上为固壁边界,而槽道只有法向为固壁边界,这可以被认为是差异产生的主要原因。方管中对角线上的平衡位置,随着Re数从100增加到1500,逐渐向管壁靠近,直至颗粒中心距管壁约为0.2H处,这与实验中结果相似。方管边线中间处的平衡位置,随着Re数的增加,先靠近壁面,在Re数增加到800附近后,反而出现向方管中心迁移的现象,形成类似于圆管的内部平衡点。
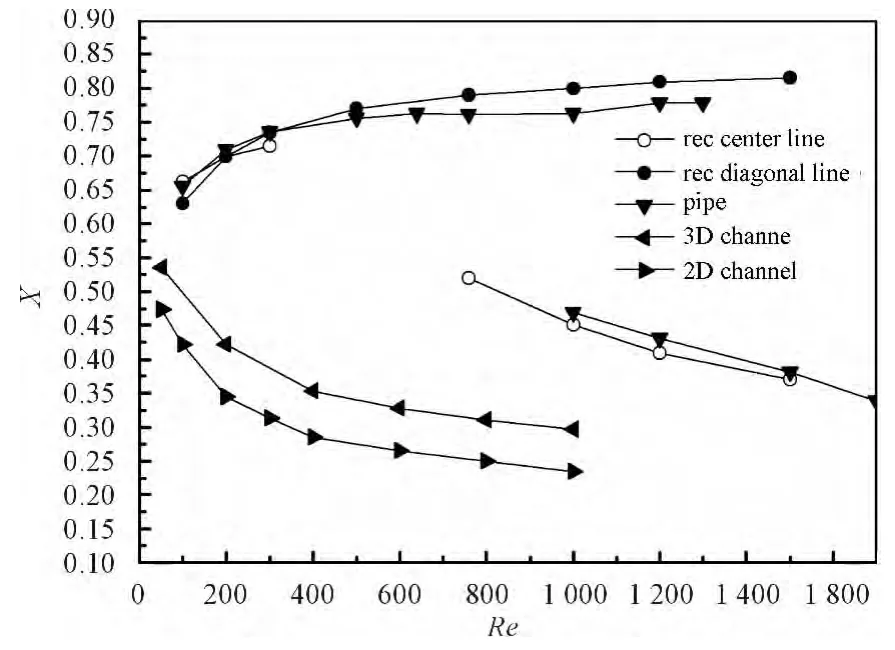
图6 a/H=0.15条件下,方管、圆管和槽道中颗粒迁移平衡位置的比较
两种不同粒径的颗粒都具有两种平衡位置,且两种位置都能够稳定存在。随着Re数的增加,3种大小颗粒的平衡位置改变的趋势相同,如图7所示。其区别主要体现在:相同Re数下,相对于大颗粒,小颗粒的平衡位置要更靠近于壁面。高Re数下,边线中部的平衡位置相差较大,大颗粒更易形成内部平衡点。
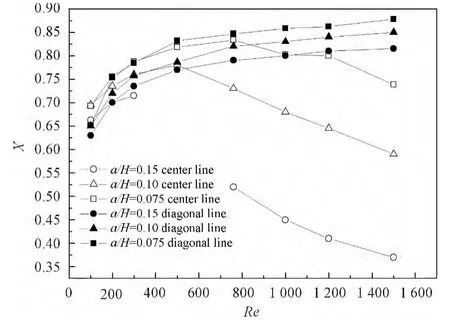
图7 a/H=0.1、a/H=0.15 和 a/H=0.075 颗粒的平衡位置
3 结束语
本研究采用并行虚拟区域方法对方管中中性悬浮颗粒惯性迁移现象进行了完全直接数值模拟,研究了雷诺数为100~1500范围内,颗粒粒径对惯性迁移现象的影响,丰富和完善了颗粒迁移运动的机理研究。研究结果表明:颗粒的迁移平衡位置分为方管对角线和边线中间两种。在周期性管长(L=2H)条件下,其平衡位置与粒径大小密切相关。稳定存在的对角线和边线中间两个平衡位置,随着雷诺数的增加,对角线上的平衡位置愈靠近角落,边线中间的平衡位置则先靠近壁面,再远离壁面,向管芯靠近;相同Re条件下,小颗粒的平衡位置比大颗粒更靠近壁面,尤其边线中部的平衡位置差别较大。高Re条件下,大颗粒更易形成类似管流中的内部平衡点。
[1]SEGRE G,SILBERBERG A.Behaviour of macroscopic rigid spheres in poiseuille flow part 2.experimental results and interpretation[J].Journal of Fluid Mechanics,1962,14(1):136-157.
[2]SEGRE G,SILBERBERG A.Behaviour of macroscopic rigid spheres in poiseuille flow part 1.determination of local concentration by statistical analysis of particle passages through crossed light beams[J].Journal of Fluid Mechanics,1962,14(1):115 -135.
[3]JEFFREY R C,PEARSON J R A.Particle motion in laminar vertical tube flow[J].J.Fluid Mech,1965,22(4):721-735.
[4]KARNIS A,GOLDSMITH H L,MASON S G.The flow of suspensions through tubes:V.inertial effects[J].The Canadian Journal of Chemical Engineering,1966,44(4):181-193.
[5]MATAS J P,MORRIS J F,GUAZZELLI E.Inertial migration of rigid spherical particles in poiseuille flow[J].Journal of Fluid Mechanics,2004,515(1):171 -195.
[6]MATAS J P,MORRIS J F,GUAZZELLI E.Lateral forces on a sphere[J].Oil & Gas Science and Technology,2004,59(1):59 -70.
[7]FENG J,HU H H,JOSEPH D D.Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid.part 2.couette and poiseuille flows[J].Journal of fluid mechanics,1994,277(271):271 -301.
[8]PAN T W,GLOWINSKI R.Direct simulation of the motion of neutrally buoyant circular cylinders in plane poiseuille flow[J].Journal of Computational Physics,2002,181(1):260-279.
[9]PAN T W,GLOWINSKI R.Direct simulation of the motion of neutrally buoyant balls in a three-dimensional poiseuille flow[J].Comptes Rendus Mécanique,2005,333(12):884-895.
[10]YU Z,PHAN-THIEN N,TANNER R I.Dynamic simulation of sphere motion in a vertical tube[J].Journal of Fluid Mechanics,2004(518):61 -93.
[11]SHAO X,YU Z,SUN B.Inertial migration of spherical particles in circular poiseuille flow at moderately high Reynolds numbers[J].Physics of Fluids,2008(20):103-307.
[12]CHUN B,LADD A J C.Inertial migration of neutrally buoyant particles in a square duct:an investigation of multiple equilibrium positions[J].Physics of Fluids,2006(18):317-320.
[13]YU Z,SHAO X.A direct-forcing fictitious domain method for particulate flows[J].Journal of computational physics,2007,227(1):292 -314.
[14]YU Z.A DLM/FD method for fluid/flexible-body interactions[J].Journal of Computational Physics,2005,207(1):1-27.
