永磁同步电动机结构的模态研究*

李 娉 马永龙

(1.湖北三江航天险峰电子信息有限公司 武汉 432000)(2.海军驻中南地区光电系统军事代表室 武汉 430074)

永磁同步电动机结构的模态研究*

李 娉1马永龙2

(1.湖北三江航天险峰电子信息有限公司 武汉 432000)(2.海军驻中南地区光电系统军事代表室 武汉 430074)

论文先简要介绍模态分析理论,再运用机电类比的方法推导定子固有频率的计算方法,并用ANSYS软件对电机定子建立的三维有限元模型进行模态分析,计算出它们的固有频率及其振型,避免和电磁力的频率及次数发生共振,从而降低永磁同步电动机的电磁振动和噪声。

永磁同步电动机; 模态分析; ANSYS

Class Number TM359.4

1 引言

永磁同步电动机的电磁振动与噪声不仅与电机中气隙磁场所产生的电磁激振力波频率、幅值和力波阶数有关,而且还与电机结构的固有频率的大小及分布有着密切的关系。通过对电机定子结构的模态分析,可以确定电机电枢结构的固有频率和振型,就可预测电机在电磁力的作用下实际振动响应。

模态分析技术从20世纪60年代后期发展至今已经有40多年的历史了。模态分析的经典性定义是:将线性定常系统振动微分方程组中的物理坐标变换为模态坐标,使方程组解藕,成为一组以模态坐标及模态参数描述的独立方程,以便求出系统的模态参数[1]。振动模态是振动系统的各点以特定的频率作简谐振动时,表示波节和波腹的振动形态或与其相应的衰减振动状态;固有模态是自由振动时系统的振动模态,与系统的各个自由度相对应,常简称为模态[2]。模态是机械及结构的固有振动特性。每一阶模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由有限元计算或试验分析取得。基于线性叠加原理,一个复杂的振动系统可以分解为许多模态的叠加。这样一个分析过程为模态分析[3]。

永磁同步电动机结构的模态分析是判断电动机定子结构是否发生共振的重要手段,电动机的电磁噪声和振动主要是通过定子、壳体向外辐射。本节主要是进行电动机结构的模态分析,由于电动机结构的几何特性决定着定子沿轴向的刚度是变化的,所以采用三维结构有限元模型来分析电动机定子及机壳结构的模态。

2 电机结构的模态分析理论

永磁同步电动机模态分析的关键在于找到模态振型矩阵,以构成模态坐标系统,并求得响应量在这一坐标系统中的坐标,具体过程如下[4]:

1) 寻找各阶模态振型,组成坐标变换矩阵{ψr}=[{ψ1} {ψ2} {ψ3} … {ψN}];

2) 进行坐标变换{X}={ψ}{q};

3) 求取模态坐标qr,r=1,2,3,…,N,从而得到{q};

4) 建立响应计算模型—模态模型;运用模态模型,便可计算在实际激励作用下的结构的运动,包括位移、速度、加速度,乃至应力应变。

2.1 质点运动方程

通过牛顿第二定律可以得到质点的运动方程:

(1)

进行拉普拉斯变换后上式可写为

s2mX(s)+srX(s)+kX(s)=F(s)

两边同除以m可变换为

则质点的位移响应为

质点的速度响应为

质点的加速度响应为

因此可得出由力到加速度的传递函数为

永磁同步电动机定子振动中,除了有电磁力引起的强迫振动,还有自由振动。下面分析永磁同步电动机的自由振动特性。令系统的运动方程(1)的右边为0,则可得系统的自由振动方程为

该方程的通解形式为

式中,C1、C2为由系统初始条件决定的常数。

故运动方程的解可表示为

对于无阻尼运动,ζ=0;对于欠阻尼运动,ζ<1;对于临界阻尼运动,ζ=1对于过阻尼运动,ζ>1。在实际的振动系统中,一般都是欠阻尼运动,否则就不会形成振动了。则对于欠阻尼情况,ζ2≪1,运动方程的解可写为

2.2 永磁同步电动机振动特性的机电类比分析

图1 电机定子机电类比双环型模型

永磁同步电动机一般选用同容量的异步电机机座,定子铁心与机壳内圆采用过盈配合,无连接筋。设定子铁心轭的刚度为K1,质量为m1,机壳的刚度为K2,质量为m2,不考虑绕组、定子凸极的影响,散热筋、底脚、接线盒的质量归入机壳质量;并设各部分的阻尼系数分别为rm1、rm2(假设各部分阻尼比为粘性,且等于钢或铸铁的阻尼比),则其物理模型、机械网络图、等效电路图如图1所示[5～6]。

图中p0为作用在定子铁心内表面上单位面积力的幅值,pn为等效的集中力,即:

Pn=2πRilaP0

式中,Ri为定子磁轭的内半径,la为定子铁心轴向长度。

由机电类比法[7]可得对应角频率ω的总机械阻抗为

则定子振动位移的幅值为

(2)

式中,铁心及机壳的刚度和质量为[3]

(3)

(4)

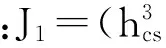
设定子铁芯、机壳的阻尼比ζ1、ζ2为粘性,则阻尼系数为

令机械阻抗的虚部为零,可求得定子的固有频率为

(5)

共振时,定子振动位移的振幅为

将式(3)、(4)代入式(2)、(5),可得电机强迫振动幅值和固有频率为

(6)

(7)

由式(6)～(7)可得永磁电机轴向阶数为零的平面振动特性[6],即:

1) 振动幅值与力波幅值成正比。因此减小力波幅值是控制振动的主要措施之一;

2) 随着振形阶数n的增大,对应的固有频率近似以n2的比例增大,而振幅则近似以n4的比例减小,因此,阶数较低的力波引起的振动应是防范的重点;

3) 定子直径越大,固有频率越低,亦即当激励力的振幅、频率均相等时,几何尺寸越大的电机,振动幅值越大,因而磁噪声级亦越大;

4) 振动大小与振动系统的阻抗Zm关系很大,阻抗表明振动系统接近谐振的程度。谐振时振动甚至在小的电磁激振力时都可能很大。因此,使固有频率避开主要的力波频率是减小振动的主要措施之一;

5) 共振时激振力波与振动速度同相位,这时振动幅值完全由阻尼限制。

3 永磁同步电动机定子模态分析

目前,理论计算固有频率的方法有两大类:一类是解析解计算方法,典型的是机电类比法,该方法可以得到固有频率的解析表达式,但是计算精度较差;另一类是能量法,它有两种解法,一种是傅里叶级数解法,另一种是有限元法。一般情况下,两种解法都不能得到解析解,而只能得到数值解。在定子结构对称时,傅立叶级数的求解精度可满足一般工程上的要求。有限元解法可以考虑定子结构的不规则性,其计算精度较高。由于电机结构复杂,用解析法计算虽然简便,但计算误差较大,因此本文采用有限元方法仿真计算了电机的模态,研究了电机的定子铁心的模态。

用户使用ANSYS的模态分析来决定一个结构或者机器部件的振动频率(固有频率和振型)。ANSYS产品家族的模态分析是线性分析。任何非线性特性,如塑性和接触(间隙)单元,即使定义了也将被忽略。

需要记住以下两个要点[8]:

1) 模态分析中只有线性行为是有效的,如果指定了非线性单元,它们将被当作是线性的。例如,如果分析中包含了接触单元,则系统取其初始状态的刚度值并且不再改变此刚度值。

2) 必须指定弹性模量EX(或某种形式的刚度)和密度DENS(或者某种形式的质量)。材料性质可以是线性的或非线性的、各向同性或正交各向异性的、恒定的或与温度有关的,非线性特性将被忽略。用户必须对某些指定的单元(COMBIN7,COMBIN14,COMBIN37)进行实常数的定义。

3.1 基于能量法的电机振动模态的有限元分析模型

作为有限元法的一种,能量法的基础是拉格朗日方程。在能量法计算中,一般用广义坐标来描述系统,将系统的动能和势能等表示为广义坐标及其导数的函数[9]。系统的拉格朗日运动方程可表示为

其中,L=T-U为拉格朗日函数,T为系统动能,U为系统势能,Fi为系统非保守广义力,qi为广义坐标,i=1,2,3…。

在有限元解法中,单元的动能为

势能为

单元的刚度矩阵为

依据Hamilton原理和应力—应变、应变—位移的关系[10],可导出电机离散后单元的运动方程为

将各个离散的单元方程组联合成总的系统方程组,经过整理则可得出系统标准的运动方程为

(8)

([K]-ω2[M]){u}={0}

(9)

根据线性方程组理论有非零解的充分必要条件为

|[K]-ω2[M]|=0

(10)

解出满足方程(9)、(10)的频率ω2和对应的非零解向量{ur}(r=1,2,3…),则ωr,{ur}分别为电机结构的固有频率和固有振型。

有限元法ANSYS软件提供了子空间法、分块Lanczos法、Power Dynamics法、缩减法、非对称法、阻尼法和QR阻尼法七种模态提取方法。大多数分析都选用前四种求解方法,非对称法和阻尼法只在特殊情况下会用到。本文主要采用分块Lanczos方法对问题展开求解。此方法应用于提取大模型的多阶模态,经常应用在具有实体单元或壳单元的模型中,特别是在模型中包含形状较差的实体和外壳单元中,它的计算速度很快,但要以消耗内存为代价[11]。

分块Lanczos法的特征值求解器采用缺省求解器,它采用Lanczos算法,是由一组向量来实现Lanczos递归运算。这种方法和子空间法一样精确,但速度更快。无论EQSLV命令指定过何种求解器进行求解,分块法都将自动采用稀疏矩阵方程求解器。计算某系统特征值谱所包含一定范围的固有频率时,采用这种方法特别有效。计算时,求解从频率谱中间位置到高频端范围内的求解收敛速度和求解低阶频率时基本上一样快。因此,当采用频移频率(FREQB)来提取从FREQB(起始频率)的模态时,提取大于FREQB的n阶模态和提取n阶低频模态的速度基本相同。在本节的计算中均采用了这种方法。

3.2 定子铁芯的模态分析

永磁同步电动机定子铁芯的弹性模量通常取2.05～2.15×1011N/m2,密度为7305kg/m2,泊松比是0.3。采用有限元软件进行模态仿真时,模型选用的单元类型为PLANE82,分析类型选用分块的兰索斯(Block Lanczos)法,求解的模态数选择为40,扩展的模态数选择为40。图2是定子铁芯三维有限元模型,图3是模态分析后的固有频率及振型。

图2 定子铁芯三维有限元模型

(a) 二阶振型

(b) 三阶振型

(c) 四阶振型

(d) 五阶振型图3 定子铁芯模态分析的固有频率及振型表1 永磁同步电动机定子三维模型的振型和固有频率

振型固有频率振型固有频率二阶1618Hz 1620Hz2251Hz 2253Hz四阶5300Hz 5317Hz6225Hz 6228Hz7536Hz 7603Hz三阶3791Hz 3805Hz4602Hz 4612Hz4886Hz 4893Hz五阶8317Hz 8431Hz9542Hz 9553Hz1174Hz1183Hz

从表1中可以看出三维定子模型更加接近实际模型,可以得到丰富的模态和固有频率信息。有些频率相近是由于电机定子结构是对称的,会出现振型和频率相同但相位不同的情况;考虑永磁同步电动机定子结构的固有模态,有利于避免电磁共振,减少振动幅值,从而有利于降低电磁振动和噪声。

4 结语

本文运用机电类比的方法推导出了定子固有频率的计算方法。利用有限元分析软件ANSYS建立了永磁同步电动机样机定子的三维有限元模型,计算得到了样机的振型及振动固有频率的关系,从而为避免共振起到了预见性作用,为高转速和低噪声的永磁同步电动机定子设计提供理论参考。

[1] 袁安富,陈俊.ANSYS在模态分析中的应用[J].中国制造业信息化,2007,36(11):42-44.

[2] S. J. 杨著.低噪声电动机[M].北京:科学出版社出版,1985.

[3] 张培强,冯文琴.现代实验模态分析的基本原理[J].武汉水运工程学院学报,1984,(4):99-115.

[4] 李德葆.振动模态分析及其应用[M].北京:宇航出版社,1989:57.

[5] 陈永校,诸自强,应善成.电机噪声的分析与控制[M].杭州:浙江大学出版社,1987:1-200.

[6] 孙剑波.开关磁阻电机的减振降噪和低转矩[D].武汉:华中科技大学,2005.

[7] 王宏华,王治平,江泉.开关磁阻电动机固有频率解析计算[J].中国电机工程学报,2005,25(12):133-135.

[8] 王建江,胡仁喜,刘英林,等.ANSYS11.0结构与热力学有限元分析实例指导教程[M].北京:机械工业出版社,2008,3.

[9] 盛剑霓.工程电磁场数值分析[M].西安:西安交通大学出版社,1991.

[10] 吴建华.基于物理模型开关磁阻电机定子模态和固有频率的研究[J].中国电机工程学报,2004,24(8):109-114.

[11] 佟宁泽.大中型感应电机电磁力及定子振动分析[D].沈阳:沈阳工业大学,2006.

Model Analysis of Permanent Magnet Synchronous Motor

LI Ping1MA Yonglong2

(1. Hubei Sanjiang Aerospace Xianfeng Electronic Information Co., Ltd., Wuhan 432000) (2. Navy Representative Office in EO System of Central-South Area, Wuhan 430074)

The paper introduces the theory of the model analysis. The electromechanical analogy method is used to derive the calculation method of the natural frequency of the stator, and the ANSYS software is used to set up motor stator three-dimensional finite element model and model analysis. The natural frequency and vibration mode are calculated to avoid resonance of frequencies and force with electromagnetic force then reduce electromagnetic vibration and noise of PMSM.

permanent magnet synchronous motor, model analysis, ANSYS

2013年8月5日,

2013年9月27日

李娉,女,工程师,研究方向:电子信息、技术改造等。马永龙,男,硕士,工程师,研究方向:舰船电子。

TM359.4

10.3969/j.issn1672-9730.2014.02.041