基于自适应加权的船舶操纵性能多目标优化*
2014-07-05周猛猛黄卫刚
周 奇 陈 立 周猛猛 许 辉 黄卫刚
(中国舰船研究设计中心 武汉 430064)
基于自适应加权的船舶操纵性能多目标优化*
周 奇 陈 立 周猛猛 许 辉 黄卫刚
(中国舰船研究设计中心 武汉 430064)
针对多目标优化问题中固定加权和法存在的缺陷,提出以设计者期望目标值为约束的自适应加权和法。以水面船舶为研究对象,建立操纵性能多目标优化数学模型。35000吨级原油船算例表明基于自适应加权法求解操纵性优化模型能获得较为理想的Pareto最优前沿。最后,采用信息熵权TOPSIS法对Pareto方案排序供决策者选择。
操纵性; 多目标优化; 自适应加权; TOPSIS
Class Number U661
1 引言
船舶的操纵性是船舶的重要性能之一,与航行的安全性、经济性以及军舰的战斗力和生命力有着密切关系。传统的船舶设计中,往往以浮性、稳性快速性来决定船舶的主尺度,船舶的操纵性设计只是参考母型船进行舵设计。随着造船工业的飞速发展,船舶日益大型化、高速化和专用化,航运密度提高,海损事故剧增,给人类生命财产和海洋生态环境带来了很大的威胁。自1982年国际海事组织(IMO)提出了“评定船舶操作性能的指导书(草案)”以来,各国相继制定了船舶操纵性标准,我国根据现有条件也制定了相关的海洋船舶操纵性衡准。将操纵性和快速性、稳性一样纳入船舶优化设计流程之中,有利于提高船舶总体性能。
船舶操纵性能涵盖诸如直线稳定性、回转性、航向改变性等多方面的内容,因此操纵性能优化设计属于多目标优化的研究范畴。国内已有学者对操纵性的衡准和优化进行了研究[1~3],大多是基于经典的多目标处理方法(固定加权和法)将多目标问题转换为单目标后求解。这种做法继承了单目标算法计算成本低、程序编制容易的优点,但也存在一些局限性[4~5],如在求解多目标优化问题时,对Pareto最优前沿的形状很敏感,不能很好处理前端的凹部;另外,对于某些问题,与应用背景相关的启发式知识不能获得,缩小了寻优空间,易陷入局部最优。
本文对传统的固定加权和方法加以改进,采用以设计者期望目标为约束,自适应调节加权系数,产生一系列权值代替固定权系数,然后采用序列二次规划算法对单目标优化问题求解,构成pareto解集。这种方法克服了固定加权和法对Pareto前沿形状敏感的弱点,同时,相对于基于Pareto意义的多目标遗传算法程序简单,易于实现,具有较快的收敛效率。最后,以一艘35000吨级原油船为研究对象,结合船舶初步设计阶段的具体情况,选取直线稳定性指数、相对回转直径为优化目标,构建船舶操纵性多目标优化数学模型,应用熵权TOPSIS(Technique for Order Preferenceby Similarity to Ideal Solution)法给出了自适应加权操纵性多目标优化Pareto解集排序方案。
2 基于自适应加权和法的多目标优化
2.1 多目标优化问题的概念
多目标优化问题可以表述为
maxF(x)=[f1(x),f2(x),…,fq(x)]
x=[x1,x2,…,xm]
s.t.gi(x)<0i=1,2,…,n
hj(x)=0j=1,2,…,t
(1)
式(1)中:fi(x)(i=1,2,…,q)为目标函数;x=[x1,x2,…,xm]为设计变量;m、q、t、n为设计变量、目标函数、等式约束条件、不等式约束条件的个数。
在多目标优化中,各目标之间通过设计变量相互制约,对其中一个目标优化必须以牺牲其它目标作为代价,因此很难找到真正意义上的最优解。与单目标优化问题的本质区别在于多目标优化问题的解不是唯一的,而存在一系列解,其特点为至少存在一个目标优于其他所有的解,这样的解称之为非支配解,或Pareto解,这些解的集合即为Pareto最优解集。

图1 基于自适应加权和的 多目标优化求解流程
2.2 基于自适应加权和的多目标优化求解流程
在多目标转化为单目标过程中,采用自适应调节形式进行权值的选取,以保证优化目标值接近期望目标限定值。其中单目标优化求解采用序列二次规划法。对于具有m个设计变量,n个约束条件,q个目标函数的优化问题,基于自适应加权的多目标优化求解流程图如图1所示。具体步骤如下:
1) 借鉴专家经验,对q个目标函数赋予初始权值wi,将多目标优化问题转化为单目标问题。即:

(2)
2) 采用试验设计的方法获取初始设计点。
采用试验设计的方法能够保证初始设计样本点的分散性与均匀性,能减少运算量,提高收敛效率。
3) 采用序列二次规划法求解单目标优化问题,获取优化一组解。
4) 以决策者期望目标值为阈值,判断q个优化目标值是否都达标,若达标,则输出优化结果,否则自动调整目标权重值。
5) 重复步骤1)~4)多次,由于权重值选取的随机性,多次运行就能获得多组达到设计者期望的Pareto解。
3 基于熵权TOPSIS法的决策体系
熵(Entropy)的概念来源于热力学,表示不能用于做功的热能,后由数学家Shannon引入信息论。在信息论中,用信息表示系统的有序程度,用熵的概念表征系统的无序程度。当系统可能处于n种不同状态,每种状态出现的概率为pi(i=1,2,…,n)时,定义系统的熵为
(3)

一般来说,多属性评价中某项指标的指标值变异程度越大,信息熵越小,则该指标信息量越大,在综合评价中重要程度就越高,赋予权重应该更大;反之,该指标的权重则越小。
TOPSIS法,又称逼近理想解排序法,是系统工程有限方案多目标决策分析常用的一种决策方法[6],它借助于多属性问题的理想解和负理想解给备选方案中各方案排序。具有原理直观,计算简便,对样本属性要求不高的优点。被广泛应用于工程风险评估[7]、医疗服务评价[8]、物流配送选址[9]等领域。
将信息熵法与TOPSIS法结合对多目标问题决策,能合理利用客观数据信息,降低评价过程中的主观因素和不确定因素,给出真实有效的方案序列。
4 应用实例
本文讨论一艘载重量35000吨级原油船。操纵性多目标设计优化数学模型简述如下:
4.1 设计变量
选取:船长L(m),船宽B(m),方形系数CB,吃水T(m),舵的宽度bR(m),舵的高度hR(m)这6个参数作为优化设计变量。即X=[L,B,T,CB,hR,bR]T
4.2 目标函数
结合我国操纵性规范及在客货船初步设计阶段的具体情况,选取直线稳定性和回转性能作为优化目标。其中,直线稳定性指数C′越大,表明船舶稳定性越好,相对回转直径D′越小,表明船舶反映灵敏度高。即优化目标表述为
MaxC′;MinD′
两个指标的表达式如下:
(4)

(5)
(6)
(7)
(8)

(9)
附加质量系数采用回归公式[10]:
(10)
相对回转直径D′的计算采用Lyster和Knights的回归公式[11]:
(11)
式中,δ为舵角,Ab为艏部浸湿面积,Trim为船舶纵倾。
4.3 约束条件
设计变量的限界约束条件为
160 0.65 根据操纵性衡准规范,参照实船操纵性试验资料,对直线稳定性指数C′、相对回转直径D′约束为 0.0035 其它约束条件包括: 其中排水量为Δ=ρLBTCB,式中ρ为海水密度。 4.4 优化结果与方案排序 以C′、D′约束为加权值调节依据,自适应调节加权因子500次,获取86个满足要求的优化解,构成Pareto最优解集如图2所示。为了比较本方法的可靠程度,图中同时给出了基于非支配解排序多目标进化算法(NSGA-Ⅱ)[12]的优化结果。图中可以看出,本文方法与NSGA-Ⅱ优化结果吻合度良好。 图2 Pareto最优前沿结果比较 船舶操作性多目标优化问题还是一个多属性决策问题。当Pareto最优解集求出来之后,还需要根据决策理论,挑选出最后的折中解或最优解。基于信息熵法,以优化解构造86×2的初始决策矩阵,通过计算,可以得到直线稳定性指数C′和相对回转直径D′属性权重值分别为 wC′=0.8678;wD′=0.1322 由属性权重可以反映出优化数据样本中相对回转直径D′变异程度较低,提供的信息量也小,赋予权重则小。表1给出了TOPSIS法综合评价指数IF前2的方案A和方案B具体优化参数。在图2中用A、B标识。 表1 优化方案A、B优化参数 船舶操纵性能优化即是利用操纵性能指数来优选船舶主尺度、船型系数及舵参数,以使船舶操纵性能最优。本文通过对一艘载重量35000吨原油船进行操纵性多目标优化设计时舍弃了传统固定加权和法将多目标问题转化为单目标求解的方法,而是基于设计者对目标函数值的约束,采用自适应加权和的形式给出了Pareto最优解集。自适应加权是对固定加权形式的延伸,能提供设计者选择的多种设计方案,且相对于基于Pareto意义的多目标遗传算法程序简单,易于实现。基于信息熵权的TOPSIS排序能避免人为决策的随意性,给出的决策序列客观、可信。 [1] 李密,刘江波,杨松林.高速单体船航行性能综合优化的遗传混沌算法[J].中国舰船研究,2008,3(1):23-27. [2] 王志东,朱仁庆,杨松林.船舶操纵性能优化设计方法研究[J].造船技术,2001,6(10.11):10-11. [3] 王志东,杨松林,朱仁庆.船舶操纵性能优化中隶属函数及权重的确定方法[J].华东船舶工业学院学报(自然科学版),2002,16(2):11-14. [4] Ray T, Gokarn R P, Sha O P. A global optimization model for ship design[J]. Computers in Industry,1995,26(2):175-192. [5] 潘治,李学斌.改进的多目标优化算法及其在船舶设计中的应用[J].中国造船,2010,51(2):99-106. [6] Dashti Z, Pedram M M, Shanbehzadeh J. A multi-criteria decision making based method for ranking sequential patterns[C]//International MultiConference Of Engineers And Computers Scientists March,2010:17-19. [7] Wang Y M, Elhag T. Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment[J]. Expert Systems with Applications,2006,31(2):309-319. [8] 周伟,王文英,袁兆康.江西省11地市城市社区卫生服务中心服务能力评价[J].中国全科医学,2013,16(1):26-28. [9] Kannan G, Pokharel S, Sasi Kumar P. A hybrid approach using ISM and fuzzy TOPSIS for the selection of reverse logistics provider[J]. Resources, conservation and recycling,2009,54(1):28-36. [10] 范尚雍.船舶操纵性[M].北京:国防工业出版社,1988,118. [11] 吴秀恒,刘祖源,施生达.船舶操纵性[M].北京:国防工业出版社,2005. [12] Deb K, Agrawal S, Pratap A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-Ⅱ[J]. Lecture notes in computer science,2000,1917:849-858. Application of Adaptive Weighted-sum Method in Ship Maneuverability ZHOU Qi CHEN Li ZHOU Mengmeng XU Hui HUANG Weigang (China Ship Development and Design Center, Wuhan 430064) Facing the shortcomings of the fixed weighted-sum method in multi-objective optimization, an adaptive weighted-sum method relying on designers’target expectations is presented. Then, the mathematical model of ship maneuverability performance is eatablished. Taking a crude oil tanker as an example, the optimization results show that the adaptive weighted-sum method can obtain a fine Pareto solution. Finally, information entropy weighting TOPSIS method is used to rank the solution series. maneuverability, multi-objective optimization, adaptive weighted-sum method, TOPSIS 2013年8月4日, 2013年9月27日 周奇,男,硕士研究生,研究方向:舰船总体多学科优化、决策。陈立,男,研究员,研究方向:舰船总体性能优化。周猛猛,硕士研究生,研究方向:舰船结构优化。许辉,女,工程师,研究方向:舰船水动力性能优化。黄卫刚,男,工程师,研究方向:舰船水动力。 U661 10.3969/j.issn1672-9730.2014.02.010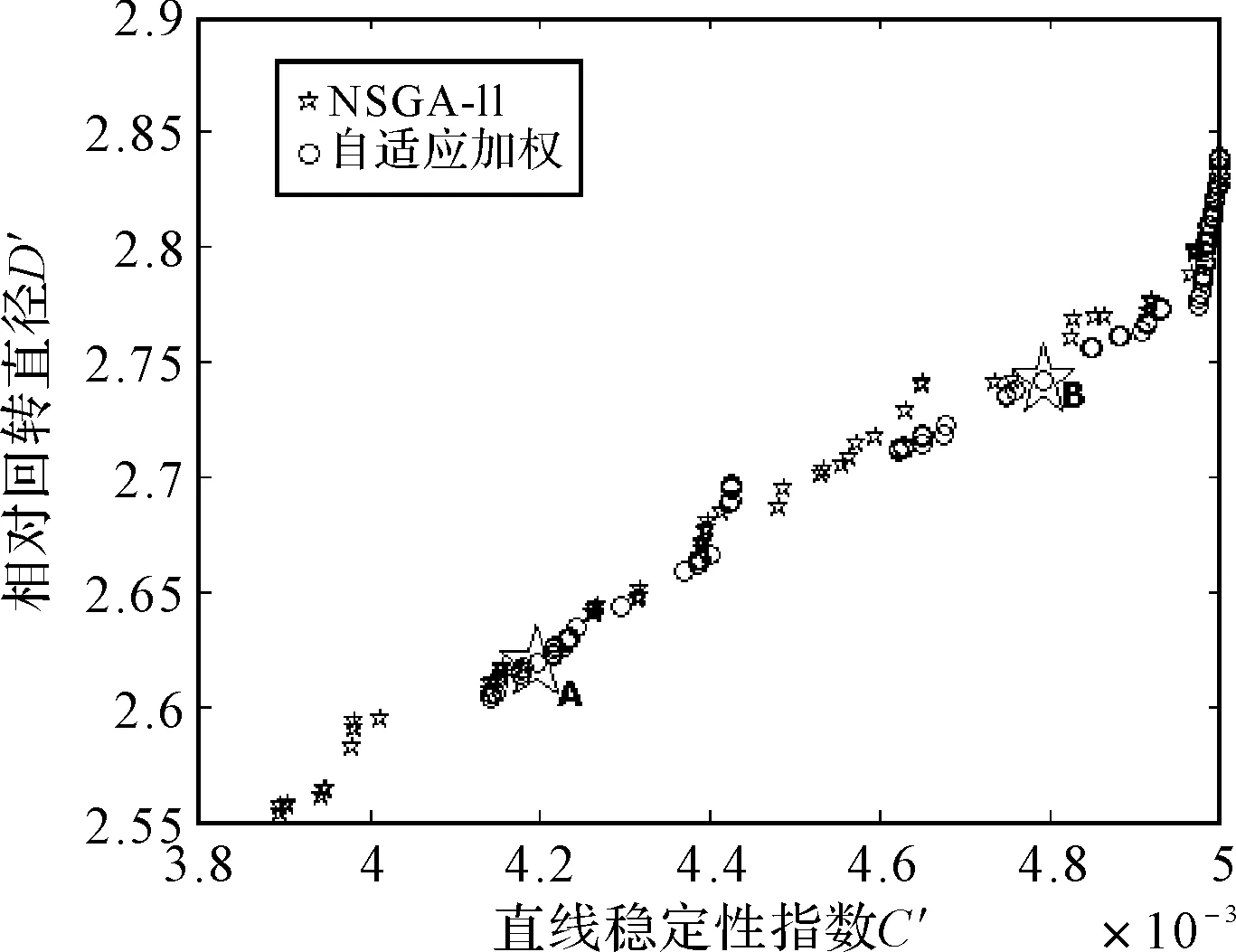

5 结语
