基于K均值聚类的传输函数设计方法
2014-07-03陈基伟向俊利杨同满
陈基伟,范 茵,向俊利,李 骞,周 蕊,杨同满
(解放军理工大学气象海洋学院,江苏 南京 211101)
0 引言
体绘制是一种重要的三维数据场可视化技术[1],它不需要生成中间几何图元,直接将三维数据场转换为二维图像,依据不同透明程度的设置让图像拥有三维显示效果。利用体绘制技术对三维数据场成像,能够准确反映数据场内部特征信息,达到在一幅图中全面显示所有数据场信息的目的。基于上述的优点,体绘制技术广泛应用在科学计算、工程计算、医学扫描等数据的可视化中,并取得了很好的发展。
体绘制的关键是传输函数设置[2],传输函数将数据值进行分类并映射为图像属性(如不透明度等光学属性)。体绘制效果取决于传输函数,传输函数的设计已成为体绘制技术中最重要的研究问题之一。
传输函数又分为一维传输函数和多维传输函数[3-4]。当面对复杂的三维数据场,一维函数显然不能很好地对数据进行处理,为了克服一维传输函数带来的局限,国内外学者进行了深入的研究,一个很好的解决方案是扩展传输函数构建多维函数。Kindlmann等人研究了利用一阶梯度和二阶梯度来对数据进行分析进而设计传输函数[5-6],基于这种方法设计出来的多维函数能对复杂数据场取得较好的体绘制效果。Wang等人通过采用二维特征空间内的高斯混合模型设计出椭圆形的传输函数[7],对传输函数的准确度和设计效率有了一定的提升;Fujishiro等人通过分析体数据的拓扑结构及其变化的信息来指导体绘制传输函数的设计[8],也得到了较好的实验结果;Levoy提出了将体数据内部同一要素不同区域和不同要素边界附近的体素赋予较小的不透明度[9],从而在采样的时候可以表现出更多的细节部分,采用这种办法得到的体绘制效果明显改善了物质细节部分的表现;Sereda采用数据灰度直方图提取物质的边界来设计传输函数[10],显示效果也有一定的改善;Caban等人提出并研究了一种基于纹理特征的传输函数,每个体素在添加了纹理特征以后,体绘制结果中体素的结构得到了明显的区分[10];Bajaj等人提出了一种基于等值面(ISO-value)传输函数设计方法[11],首先利用体数据计算得出相关等值面的平均梯度、面积和拓扑结构等特征信息,并将这些信息反馈到传输函数设计过程,然后基于这些已知的特征信息设计传输函数,得到了较为理想的绘制结果。
从现有的传输函数设计方法可以看出,基于数据中心的传输函数设计方法(如利用高维直方图信息)缺乏直观的用户交互;基于交互式传输函数设计模式的设计方法,用户可以很好地进行交互,但是缺乏自动化的数据分析来进行传输函数设计。同时,上述方法并未考虑融合多种数据时突出显示用户感兴趣的特征区域。基于上述的考虑,本文提出一种基于K-means聚类[12]的高维传输函数的设计方法。本文方法在利用K-means聚类方法设计传输函数时,对所采用的气象台风数据进行了分类,在考虑当前通用的体素特征信息基础上,压缩简化了高维空间数据,提供了便于用户交互的传输函数设计界面参数,并最终完成基于台风数据的体绘制,达到了快速便捷绘制出体数据结构特征和对用户感兴趣区域进行突出显示的目的。
1 K均值聚类算法
K均值聚类算法是由J.B.MacQueen于1967年提出的一种被广泛应用于科学研究和工业应用领域的数据挖掘经典分类算法[13-15],其核心思想是将需要处理的N个数据划分为K个聚类,然后通过计算使每个聚类中的数据到该聚类中心平方和最小。
K均值聚类算法的工作流程图如1所示。
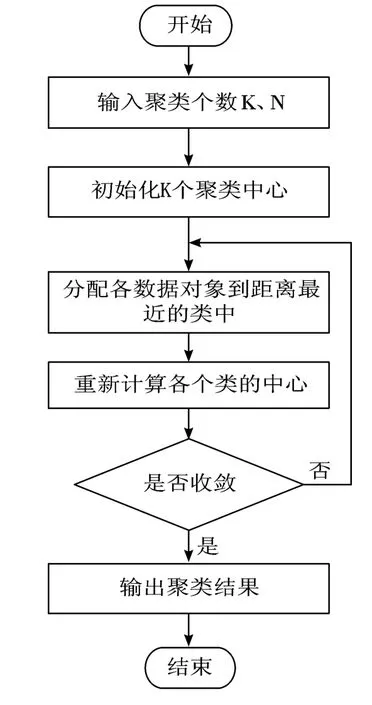
图1 K均值聚类算法的工作流程
K均值聚类算法首先选择K个对象作为初始N个数据的聚类中心,然后将剩下的对象通过与初始聚类中心进行比对,依据相似度最高原则,分类到初始聚类中心对象的集合中。接着计算每个新聚类的聚类中心(即该聚类中所有对象的均值)。不断重复这一过程直到标准测度函数开始收敛为止。标准测度函数采用均方差函数,均方差具体定义如下:

式(1)中E表示采用的标准测度函数,在这里是数据中所有对象的均方和;p表示对象空间中的某点;mi表示聚类Ki的均值。该公式表示的聚类标准旨在使所获得的K个聚类中每个聚类内部都尽可能紧凑,聚类之间的距离尽可能分开。K均值聚类算法的优点是可以处理大数量的数据集,由于它的算法复杂度是O(nkt),其中n为对象个数,k表示聚类个数,t为迭代次数,所以这种算法是相对高效率和可伸缩的。
2 算法步骤
本文算法大致可以分为5个步骤,分别是:体数据的预处理、体数据特征提取、K均值聚类算法处理、传输函数调节和基于GPU的体绘制。其流程如图2所示。
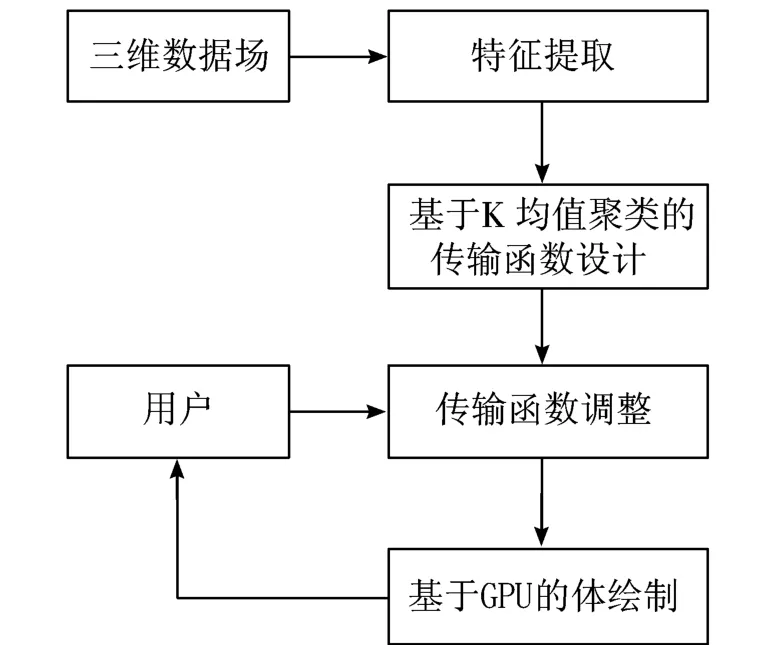
图2 本文算法流程
本文基于K均值聚类的传输函数设计方法首先对体数据进行预处理,对体数据进行滤波,剔除冗余和干扰的体素,达到加速体绘制和提高体绘制效果的目的;接着提取体数据的多种特征属性,生成体数据的特征空间;然后采用改进的K均值聚类算法对体数据特征进行分类,对于每一个分类结果,将其与体数据的局部一维传输函数相绑定,并设计相应的人机交互界面给用户参与到传输函数设计的过程中;最后采用基于GPU的光线投射算法进行体绘制中的渲染工作,得到最终输出图像。
2.1 体数据的预处理
数据预处理是把混在原始数据中的异常数据和干扰数据排除,留下尽可能多的有效数据,从而达到加快体绘制绘制速度和提高体绘制绘制质量的目的。考虑到处理速度和处理体数据所消耗的资源这2个因素,本文介绍的对体数据预处理的方法相对简单。
本文中采用体数据的位置信息和体素密度这2种属性对明显无效的体素进行剔除,达到初步预处理体数据的效果。具体操作是,设定一个阈值∈[D1,D2](D1<D2),对所有体素 f(x,y,z)的值进行阈值判定,若 f(x,y,z)的值在预设范围内并且中心(x/2,y/2,z/2)也在预设范围内,将此体素作为有效体素保留,否则剔除此无效体素。
2.2 体数据特征提取
体数据特征提取是对体数据进行分类的前提。令三维体数据场为 f(x,y,z),则三维数据场 f(x,y,z)在 x、y 和 z方向上的一阶偏导数分别为 ∂f/∂x、∂f/∂y、∂f/∂z,三维数据场在 x、y、z、xy、xz和 yz方向的二阶偏导数分别为 ∂2f/∂x2、∂2f/∂y2、∂2f/∂z2、∂2f/∂xy、∂2f/∂xz和∂2f/∂yz。本文方法将采用三维数据的梯度幅值、多阶导数、曲率、光滑度等特征作为体数据分类的根据。
2.3 K均值聚类处理
K均值聚类算法是一种基于划分的主流分类算法,被广泛应用于科学研究和工业应用中,算法相对来说简单实用高效。传统的K均值聚类算法的初始聚类中心是随机选取的,只能够选取到一个局部最优值,对于分类的准确性有一定的影响。针对这个不足,Arthur D等人提出了改进的K均值聚类算法,该方法通过改进初始聚类中心的选取方法,在提高聚类结果准确度和算法运行效率的基础上获得了聚类选取的全局最优解,因此本文采用这一思想,设计改进的K均值聚类算法对多维数据的特征空间进行聚类分析。
改进的K均值聚类算法流程如下:
令 x⊂Rd(d=1,2,3,…)是选取的数据点集(其中d表示维数),假设D(x|x∈X)表示当前被选取的最佳的聚类中心的距离。则有:
1)初始化聚类中心S1:从数据点集X中随机选取一个聚类中心S1。
2)选取聚类中心 Si(i=1,2,...,K)。令 x'∈X,采用为概率,式中D(x)2表示X中数据点x到最近的聚类中心的距离,利用Si=x'∈X选择聚类中心Si。令i=i+1,继续选取Si,到i=K时终止,即直到K个聚类被选完为止。
3)对选取的种子采用K均值算法进行聚类分析。
采用改进后的聚类算法对特征组合进行聚类运算后会产生K个分类类别,即K个聚类中心。根据实验得知,聚类中心的个数K的值对于聚类分析的结果会产生一定影响。当聚类中心数目较大时会增大计算量影响计算效率,同时分类太多导致分类结果缺少概括性,对于后续体绘制工作中的传输函数调整有较大影响;当聚类中心数目较小时,则会导致特征空间中不同的特征映射到同样的类中,聚类分析后的分类效果较差。因此,根据选取的不同特征空间,本文经过大量实验选取了不同的聚类中心个数。
本文选取了由一阶梯度、二阶梯度模值、体素灰度值、体素均值、体素空间坐标等几种特征组合而成的多维特征空间。选取了带权值的相似性测度作为2个特征空间距离的标准,通过这种方法可以更好地获取聚类分析结果。具体方法如下:
令Fi(x)为体素x的第i个特征值,其中i=0,1,2,...,n(n为选取的特征空间的维度数)。令 S(x,x0)为体素x与选择的参考体素x0的相似性测度值,ki为选择的权值且权值和为1,即∑ni=0ki=1。本文中权值初始设定为ki=1/n。因此本文中所定义的相似性测度为:

权值的大小决定其对应的特征空间的重要程度,在试验中可以对较重要的特征空间赋予较高的权值。通过赋予不同重要性的特征空间不同的权值可以使聚类分析的分类结果更加准确,导致体绘制有更好的效果。
2.4 基于分类的传输函数和体素合成
将选择的特征空间经过上述聚类算法处理后,会生成一个值在1到n的标号矩阵J(x,y,z),其中n为初始指定的分类个数。本文方法中首先产生n个初始参数函数F(1)、F(2)、…、F(n),根据产生的标号矩阵J(x,y,z)将聚类分析后的分类结果与相应的传输函数F(1)、F(2)、…、F(n)相映射。将产生的传输函数簇定义为基于分类的传输函数族[16]。
体绘制过程中颜色合成的传统方法如下:

在体绘制过程中加入传输函数后,令颜色传输函数为FC(x),不透明度传输函数为Fα(x),其中x为选取的体素的特征值,如标量值、灰度值、梯度等三维数据场特征,则可以将如上公式改进为如下公式:

根据本文采取的方法,将产生的标号矩阵与传输函数结合起来生成一个基于分类的标号传输函数,令x表示聚类分析的分类结果号,y表示体素的标量值,则颜色传输函数可以表示为FC(x,y),不透明度传输函数可以表示为Fα(x,y),上面的合成函数可以改为:

2.5 局部传输函数编辑界面
本文设计了一个简单高效的提供用户进行传输函数编辑和修正的交互界面。传输函数修正界面提供用户对传输函数簇中的n个传输函数进行简单的修改功能。本文方法产生了n个与分类结果相对应的传输函数,用户可以按需求选择其中传输函数并进行简单修改,修改方式与传统的一维传输函数修改方式相一致。

图3 传输函数调节效果界面
在图3所示界面左侧,选择需要修改的第i个传输函数,单击删除或增加可以删除或增加当前选择的第i个传输函数。拖动右侧图中某一特征与光学属性构成的笛卡儿坐标系中显示的红色圆点的位置,就可以调节第i个传输函数的定义域到值域的映射方式。
3 实验结果与分析
实验所采用的硬件环境配置如下:NVIDIA Ge-Force GTX 680显卡,Intel Core i7-3770K CPU,8G 内存。实验所采用的软件环境是:Windows 7操作系统,Visual C++6.0编程环境结合 OpenGL3.0 3D 程序接口。本文所采用的实验数据有台风莫拉克CNOP数据、伊莎贝尔台风(Hurricane Isabel)数据。针对上述台风数据,分别采用本文提出的基于K均值聚类的体绘制方法和基于灰度-梯度直方图的体绘制方法进行绘制,效果图如图4~图7所示。

图4 基于灰度-梯度直方图的台风莫拉克数据绘制结果

图5 基于K均值聚类的台风莫拉克数据绘制结果

图6 基于数据值-梯度直方图的伊莎贝尔台风数据体绘制结果

图7 基于K均值聚类的伊莎贝尔台风数据绘制结果
图4为台风莫拉克CNOP数据在基于数据值-梯度直方图的体绘制结果。图5为台风莫拉克CNOP数据在K均值聚类体绘制结果,绘制结果显示了CNOP数据分布及其内部结构,有助于从整体上对其进行分析。通过对比,本文提出的基于K均值聚类的体绘制算法相比较基于数据值-梯度直方图更能够显示体数据的内部细节部分。
图6为伊莎贝尔台风数据在基于数据值-梯度直方图的体绘制结果。图7为伊莎贝尔台风数据K均值聚类体绘制结果。从绘制效果对比来看,基于K均值聚类的算法对于伊莎贝尔台风数据的内部结构和细节层次显示得更加清楚,对于预报人员分析台风的结构和发展趋势可以起到更好的促进作用。
表1为台风莫拉克CNOP数据和伊莎贝尔台风数据在基于数据值-梯度直方图的体绘制算法绘制速度和基于K均值聚类的体绘制算法绘制速度对比。由于基于K均值聚类算法要计算体数据的多种特征,所以理论体绘制速度应该慢于基于数据值-梯度直方图的绘制方法。从表1中也可以看出基于K均值聚类算法较基于数据值-梯度直方图的算法绘制速度慢。

表1 绘制速度对比
4 结束语
本文围绕基于K均值聚类的数据分类和传输函数设计方法,主要进行了以下工作:研究了体数据的特征提取方式并提出了改进的K均值聚类数据分类方法和高维传输函数设计算法,完成了基于K均值聚类的体绘制算法,并将基于K均值聚类的体绘制算法和基于数据值-梯度直方图的体绘制算法进行了对比。实验结果表明,本文提出的基于K均值聚类的体绘制算法比基于数据值-梯度直方图的体绘制算法能消除高维传输函数设计的复杂性并且有效地考虑气象数据的结构特征,提高了气象数据的渲染效果。对于体数据内部信息的表达更加有利。
[1] 屠文洁.三维气象数据的可视化研究[D].杭州:浙江大学,2008.
[2] 孙薇薇.光线投射体绘制算法关键技术研究[D].天津:天津理工大学,2006.
[3] 谭国珍.体绘制传输函数的研究与实现[D].杭州:浙江工业大学,2009.
[4] 周芳芳,樊晓平,叶榛.基于多尺度等值面设计传输函数[J].小型微型计算机系统,2007,28(1):144-147.
[5] Kniss J,Kindlmann G,Hansen C.Interactive volume rendering using multi-dimensional transfer functions and direct manipulation widgets[C]//Proceedings of the 2001 IEEE Visualization.2001:255-262.
[6] Kindlmann G.Transfer functions in direct volume rendering:Design,interface,interaction[C]//Proceedings of the 2002 SIGGRAPH.2002:50-60.
[7] Wang Chaoli,Yu Hongfeng,Ma Kwan-Liu.Importancedriven time-varying data visualization[J].IEEE Transactions on Visualization and Computer Graphics,2008,14(6):1547-1554.
[8] Takahashi S,Takeshima Y,Fujishiro I.Topological volume skeletonization and its application to transfer function design[J].Graphical Models,2004,66(1):24-49.
[9] Levoy M.Display of surfaces from volume data[J].IEEE Computer Graphics and Applications,1988,8(3):29-37.
[10] Sereda P.Thetransfer function design for volume data rendering[C]//Proceedings of the 2004 Advanced School for Computing and Imaging.2004:17-28.
[11] Bajaj C,Pascucci V,Schikore D.The contour spectrum[C]//Proceedings of the 1997 IEEE Visualization Conference.1997:167-173.
[12] 王莉,周献中,沈捷.一种改进的粗K均值聚类算法[J].控制与决策,2012,27(11):1711-1714.
[13] 孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.
[14] 白雪峰,蒋国栋.基于改进K-means聚类算法的负荷建模及应用[J].电力自动化设备,2010,30(7):80-83.
[15] 韩敏,范剑超.单点逼近型加权模糊C均值算法的遥感图像聚类应用[J].中国图象图形学报,2009,14(11):2333-2340.
[16] 储璟骏,杨新,高艳.使用GPU编程的光线投射体绘制算法[J].计算机辅助设计与图形学学报,2007,19(2):257-262.
