基于超混沌系统的自适应图像加密算法
2014-07-03李伊林
李伊林
(江西省水利科学研究院,江西 南昌 330029)
0 引言
随着网络技术的快速发展,越来越多的信息在网络通道中进行交换,如何提高这些信息的安全性是当前密码学所面临的一个重要问题。对于数据量大的图像信息,传统意义上的加密会出现运行效率慢的问题,而借助混沌系统对图像进行加密显然可提高效率。低维混沌系统由于结构简单、易于实现等,在图像加密中有较为广泛的应用,然而也正是其方程结构上过于简单的特点导致算法易被破解[1-5]。对于高维的超混沌系统,由于其密钥空间巨大,且含有2个正的Lyapunov指数,具有更高的复杂性及更好的不可预测性,显然更适用于数字图像加密。高铁刚等[6]较早提出了一种超混沌图像加密算法,但该算法密钥与明文没有关联性,无法抵御已知明文攻击[7-8]。卢辉斌等[9]提出的新型超混沌图像加密方案与高铁刚等在加密思想方面相接近,因此也存在安全性问题。文献[10]针对王静等[8]的改良算法进行分析和攻击,发现其同样可被破解。最近,钟厚桥等[11]提出了一种基于超混沌序列的加密方案,该方案在加密过程中采取了图像置乱与置换相结合的方式,安全性较高。本文基于超混沌系统介绍了一种自适应图像加密算法,其主要思想如下:一是将明文像素信息加入到密钥序列的变换处理中,提高了密文、明文与密钥之间的敏感性;二是采取自适应加密策略,节省生成密钥序列的时间开销,提高算法加密效率;三是对前一密文像素进行非线性模加法运算产生中间密钥,利用中间密钥对当前像素执行异或加密运算,该过程不可逆,其安全性取决于密钥,符合克尔克霍夫原则。
1 超混沌系统概述及改造
本文借助文献[12]提出的超混沌系统:
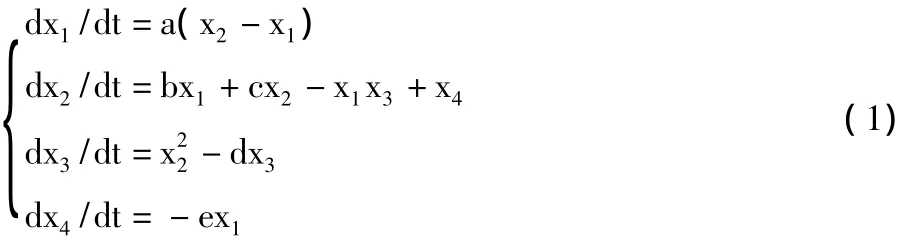
根据四阶龙格-库塔离散化算法对系统(1)进行迭代可得到原始超混沌序列。由于该原始超混沌序列的数值类型和图像像素类型不匹配,因此该序列不可直接用于数字图像加密,需要进行预先处理。
假设产生的4组原始超混沌序列为:{xj(i)},(j=1,2,3,4;i=1,2,…,L/4)。对序列各元素按式(2)进行变换处理,即取数值小数点后的第12、13、14位十进制数字组成一个新的整数xj,再将xj按式(3)组合得到长度为L的密钥序列K,式中abs()表示取绝对值,floor()表示向负方向取整,L表示算法所需密钥的数目,L=M+N,M、N分别为像素高度与宽度。
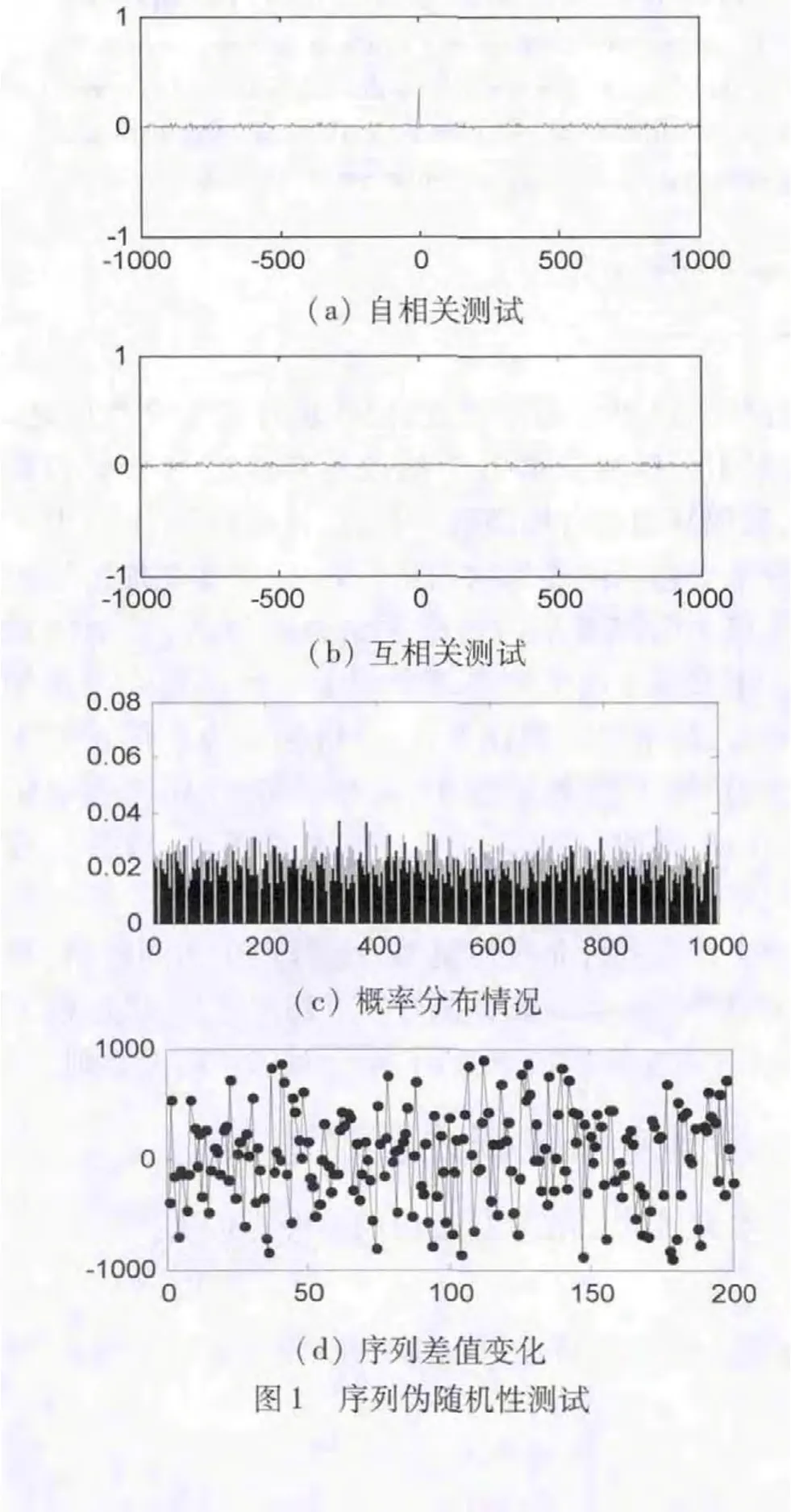
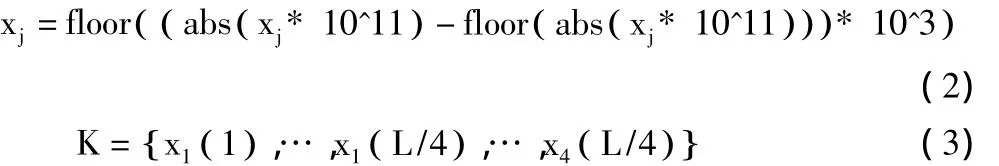
对密钥序列K进行伪随机性能检验,结果如图1所示,为防止混沌迭代暂态效应影响,测试中舍弃了前面部分初始迭代状态值。图1(a)、(b)分别是密钥序列自相关与互相关系数曲线,图1(c)是对密钥序列K连续抽取长度为10 000个数值时各值的概率分布情况,图1(d)是初值x1(0)误差为10-15时所得2组密钥序列前200个元素差值情况。由检验结果可知改造后密钥序列能够满足理想伪随机性条件。
为了使密钥序列与明文图像发生关联,再根据明文像素信息对密钥序列各元素进行如下取模运算:K=mod(S,K),式中S为原始图像像素值总和,mod()表示取余。将取模变换后的K划分成长度分别为M与N的2组密钥KM与KN。
2 自适应图像加密算法
假设原始图像为P,其像素大小为M×N,所有像素值总和为S,加密后的图像为E。将系统状态初值x=[x1(0),x2(0),x3(0),x4(0 )]载入系统(1)进行迭代,舍弃前面λ次结果后再迭代(M+N)/4次,将所得超混沌序列按前述方法进行改造处理,得到2组密钥KM与KN。
加密算法步骤如下:
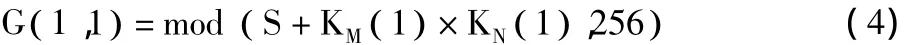
步骤2 根据中间密钥G( 1,1)按照式(5)对第1行第1个像素执行加密操作,E( 1,1)表示加密后的像素,bitxor()表示异或运算。
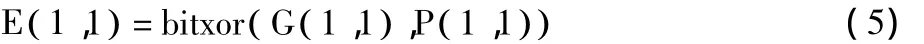
步骤1 根据式(4)得到图像P第1行第1个像素P( 1,1)的中间密钥,S表示原始图像像素值总和,KM(1)×KN(1)表示2组密钥序列KM、KN首个数值的乘积。
步骤3 利用第1行第n-1个密文像素E(1 ,n-1)按照式(6)生成第 1行第 n个像素 P(1 ,n)的中间密钥G( 1,n),n∈ (2 ,3,…,N)。
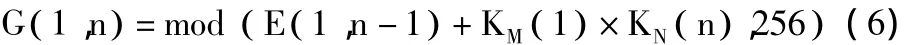
步骤4 根据中间密钥G( 1,n)按照式(7)对第1行第n个像素执行加密操作,n∈ (2 ,3,…,N)。
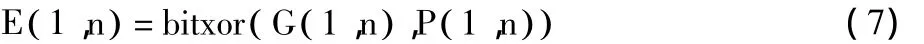
步骤5 当第1行所有像素完成加密后,以第1行密文像素E( 1,):为基础,依次生成后一行像素的中间密钥序列,即按照式(8)得到中间密钥序列G( m,:),E( m-1,:)表示上一行密文像素,m∈(2,3,…,M)。
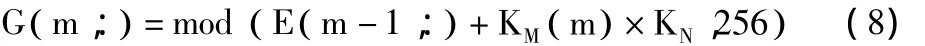
步骤6 再根据中间密钥G( m,):按照式(9)对第m行像素P( m,):执行加密操作,m∈(2,3,…,M)。
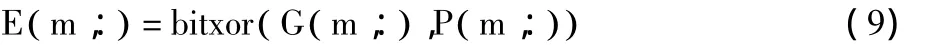
当加密操作遍历所有像素后得到最终密文图像。从加密公式可看出,每个像素均采用了不同的中间密钥进行加密操作,满足“一次一密”的密码原则,因而具有较高的安全性。
图像解密为加密的逆序过程,本算法按如下方法进行解密:
步骤1 对密文图像第M至第2行像素按式(8)、(10)执行逆序解密操
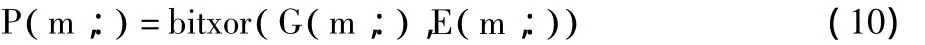
步骤2 对密文图像第1行第N至第2个像素按式(6)、(11)执行逆序解密操作,n∈(N,N -1,…,2);
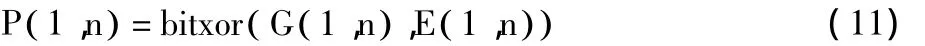
步骤3 对密文图像第1个像素按式(4)、(12)执行解密操作。
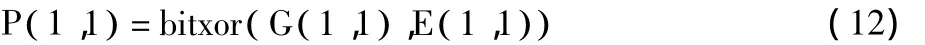
3 实验仿真与分析
态初值取 x=[1.72,3.26,2.74,1.85 ],预迭代次数 λ=100,待加密图像像素值总和为S,生成密钥序列对图像进行加解密仿真。
3.1 统计特性分析
3.1.1 直方图分析
实验中选用大小为256×256、灰度为256级的Lena等经典图像进行测试,采用Matlab 7.10作为仿真软件,实验环境为2.4 GHz的32位PC机。系统状
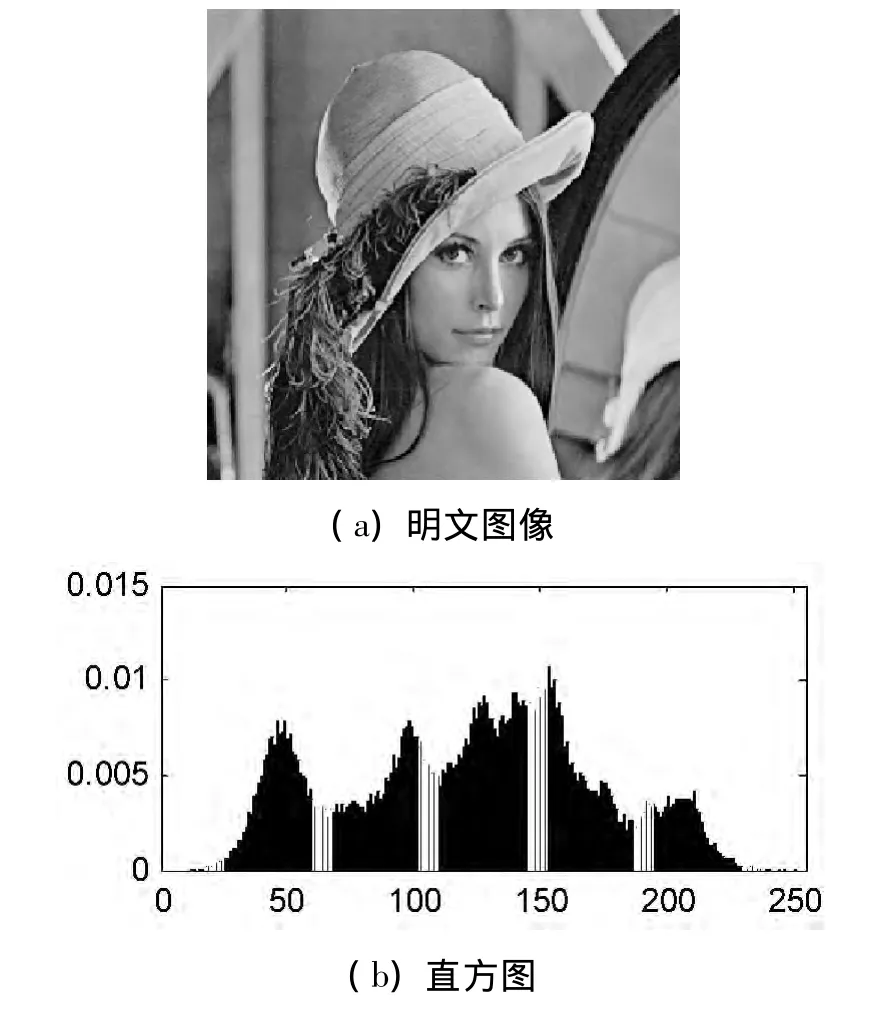
图2 明文图像及其直方图
图2、图3分别是Lena图像加密前与加密后的直观图像及对应直方图。从图2可见,原始图像灰度分布不均匀,能反映出原始图像灰度统计分布情况。而加密后图像变得杂乱无章,如图3所示,其像素值呈现平坦分布特性,各像素值取值概率趋于均等,隐藏了原始图像灰度分布情况。
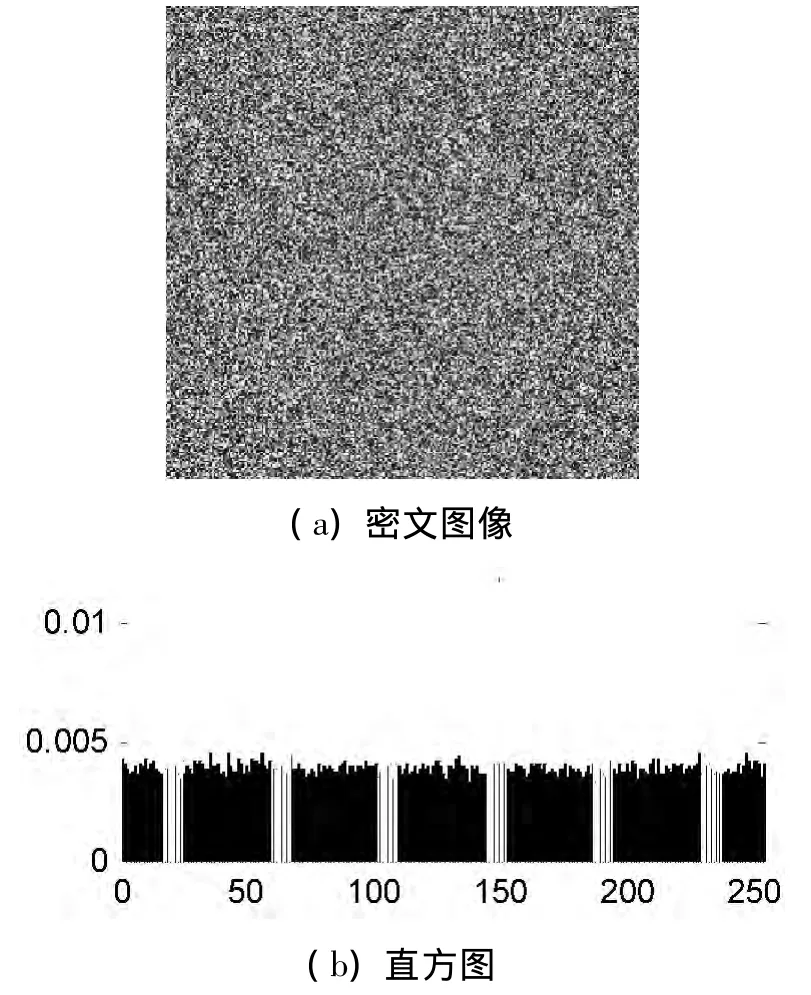
图3 密文图像及其直方图
3.1.2 相关性分析
分别选取Lena明、密文图像所有相邻像素对进行相关性统计测试,其中包括水平、垂直、对角3个方向,结果如表1所示。从表1中数据可看出,明文图像相邻像素之间存在较大的相关性,而使用本算法加密后这种相关性已基本被解除。与文献[10]与文献[13]同样方法下的相关性系数结果相对比,本算法所得相关性系数更接近于0。水平方向随机选取2000对相邻像素对在灰度值区间[0,255]分布情况如图4所示,由图4可直观地看到明文图像相邻像素点灰度值分布表现出连续性特征,加密后这种连续性被强制置乱,其相邻像素的灰度值随机杂乱出现,且近乎均匀地布满在整个灰度区域。
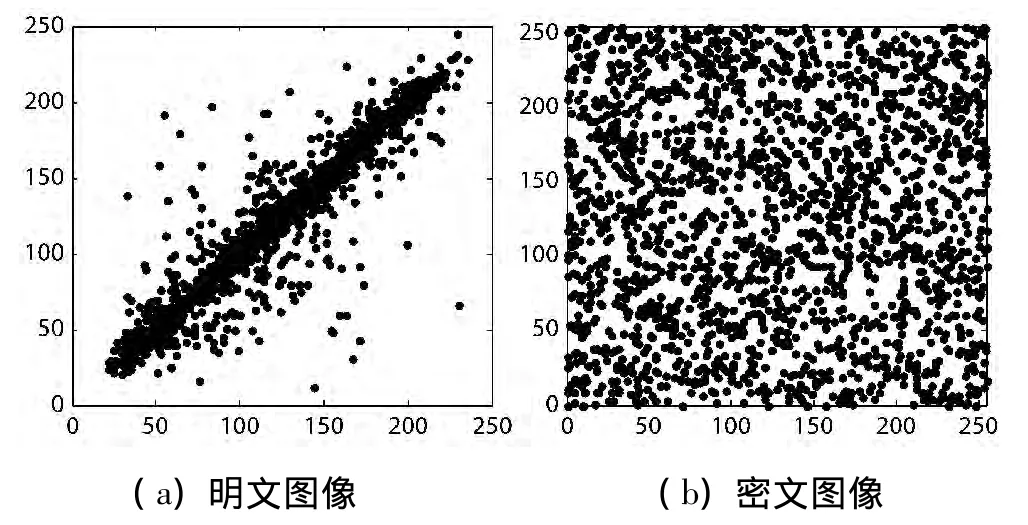
图4 图像相邻像素水平相关分布
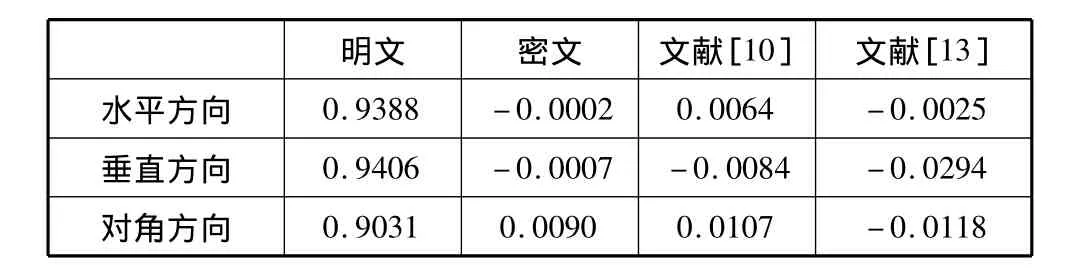
表1 相邻像素相关系数
3.1.3 信息熵分析
图像信息熵计算式如下所示[14]:
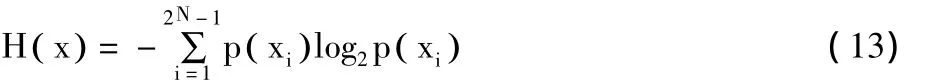
对于256级灰度图像其理想信息熵值为:H(x)=N=8。根据式(13)计算本算法得到的Lena密文图像信息熵可达到7.997,说明算法对图像置乱充分,加密算法对抵抗熵攻击是安全的。
3.2 抗差分攻击分析
像素变化率(NPCR)和平均改变强度(UACI)是衡量一个图像加密算法抵抗差分攻击的重要指标。设仅一个像素不同的2幅明文对应的密文分别为C1和 C2,各个像素分别表示为 C1(i,j)和 C2(i,j),若 C1(i,j)=C2(i,j),定义 D(i,j)=0;若 C1(i,j)≠ C2(i,j),定义 D( i,j)=1。则 NPCR 与 UACI的计算公式如下:
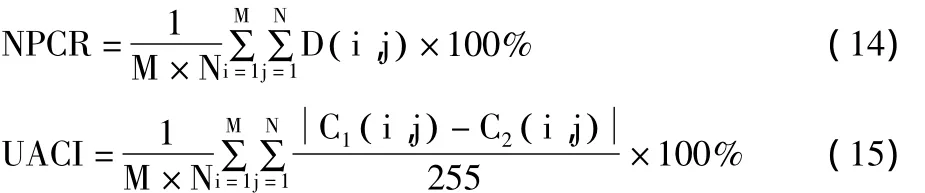
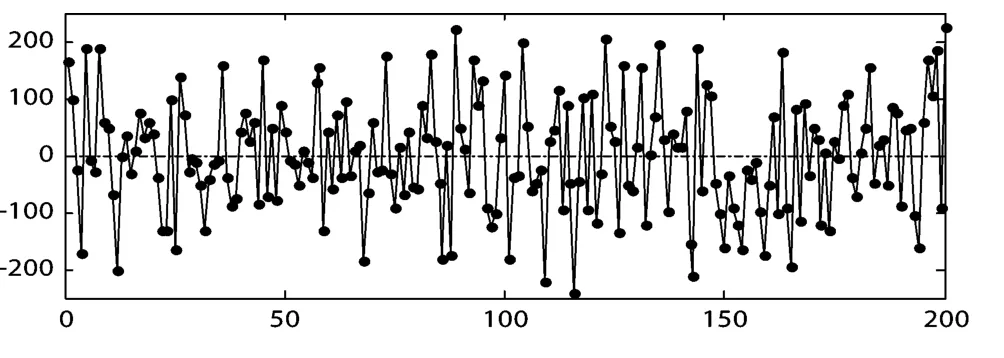
图5 密文图像像素差值
对于一幅256级的灰度图像,通过上述公式可计算得到其像素变化率与平均改变强度的理想值分别为99.6094%、33.4635%[10]。在此选取 100 组仅有一个像素值不同的Lena明文图像进行测试,且该像素点坐标在明文图像各区域随机选择。计算得到这100组密文图像的 NPCR与 UACI平均值分别为,可见所得NPCR、UACI值均非常接近理想值。同时选取一组密文图像,在不同坐标位置随机抽取200组像素对,并绘制其灰度值差曲线如图5所示。实验表明,如果明文发生微小改变,则密文会表现出极大不同,表明密文图像对明文图像高度敏感,算法可有效抵抗差分攻击。表2同时给出了文献[15-17]的相应数据值,文献[15]需要对图像进行2轮加密,文献[17]需要对图像进行3轮加密,而本文进行一轮加密后的NPCR、UACI值高于文献[15-17]相应值,说明本算法抗差分攻击能力更强。

表2 抗差分性能分析
3.3 密钥敏感测试
测试时包括以下2方面,一是微小变化的2个密钥加密同一明文图像后应得到2个不同的密文,二是微小变化的2个解密密钥解密同一密文的结果也应该截然不同[10]。
在测试前使用初值 x=[1.72,3.26,2.74,1.85]对Cameraman图像进行加密。
1)微小变化的2个密钥加密同一明文图像。
加密时选取初值密钥x2(0)误差10-15,其余参数值不变。当密钥x2(0)=3.26时随机选取密文图像100个像素绘制曲线,如图6中实线所示,同时保存这100个像素坐标位置;当密钥x2(0)=3.26+10-15时,在相同坐标位置选取100个像素绘制曲线,如图6虚线所示。同时计算2幅加密图像的NPCR、UACI值分别可达到99.6283%、33.4805%。由此可见,当微小变化的2个密钥对同一幅图像进行加密所得密文相差巨大,这体现了算法对密钥敏感。对密钥x1(0)、x3(0)、x4(0)进行同样测验,所得结果类似。
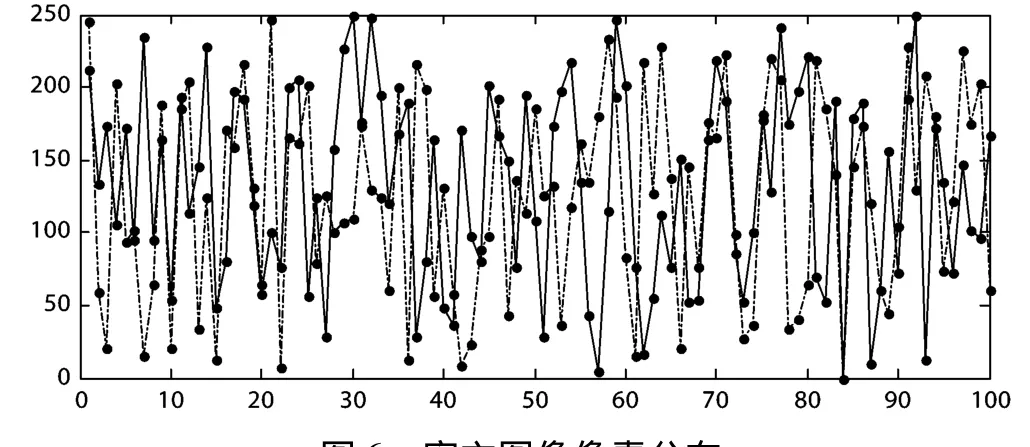
图6 密文图像像素分布
2)微小变化的2个解密密钥解密同一密文图像。
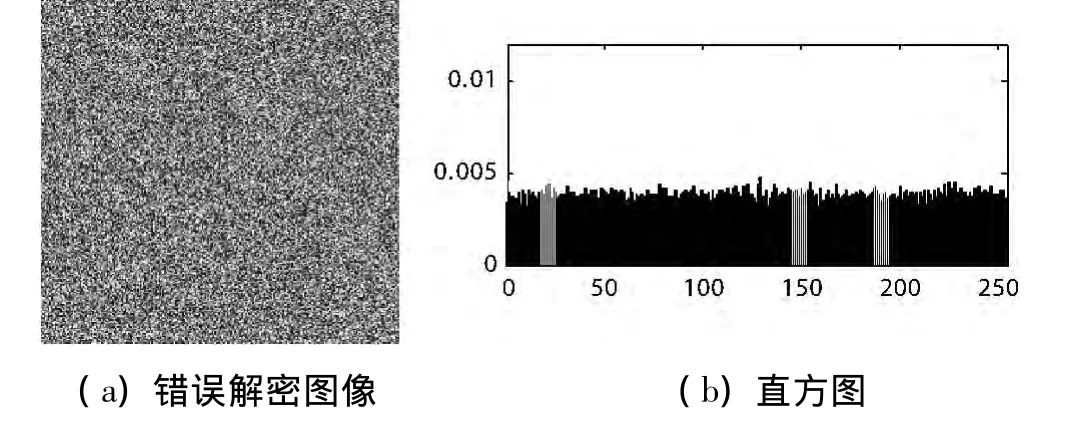
图7 错误解密图像及其直方图
解密时选取初值密钥x1(0)误差10-15,其余参数值不变,结果如图7、图8所示。图7为错误解密图像及直方图,图8为正确解密图像及直方图。可见,加密图像在密钥误差极其微小情况下解密仍是杂乱无章,图像像素值分布也仍呈现均等分布特征,验证了密钥敏感性。对密钥x2(0)、x3(0)、x4(0)进行同样测验,所得结果类似。
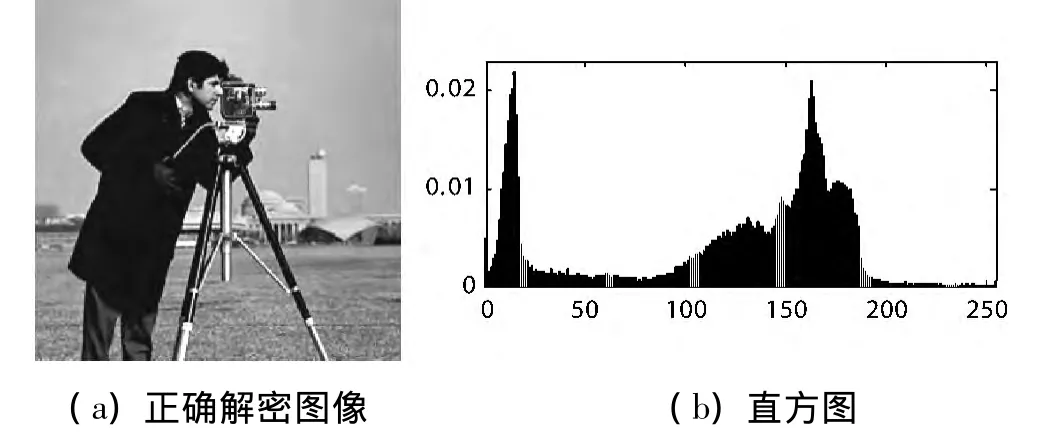
图8 正确解密图像及其直方图
3.4 密钥空间和执行效率
本文仿真时采用的数据为双精度浮点实数,可精确到小数点后15位数,则4个初值组成的密钥空间可达到:1015×1015×1015×1015=1060≈2199,可见算法密钥空间巨大。如果同时考虑预迭代次数λ和原始像素值总和S,则拥有更大的密钥空间。
本算法加密一幅大小为256×256的8位灰度图像平均时间开销为0.051 s,而文献[9]时间开销为0.82 s,相比快了约16倍,可见在运行效率方面更具优势。
4 算法性能分析
本算法采用像素自适应加密方法进行加密,其复杂度主要体现在以下几方面:
1)算法借助超混沌系统产生密钥序列,使得针对低维混沌系统的相空间重构攻击技术难于发挥作用,密文不容易被破解。同时系统密钥参数与控制参数增多,相比低维混沌系统大大扩展了密钥空间,达到了1060数量级,因此算法表现出很强的抵抗穷举攻击的能力。
2)算法中所用密钥序列与原始图像像素信息相关联,因而不同图像对应的密钥序列不同,也即若明文发生改变必然会影响密钥序列的生成,最终会导致密文图像的不同,这使得明文、密文与密钥关系非常复杂。而且从加密过程来看,用于像素加密的中间密钥均由前一个密文像素非线性运算产生,该过程具有较高的复杂性和不可逆推性,因此密码分析者要想进行反推是困难的。
3)对于一幅大小为M×N的图像,通常需要产生至少M×N个混沌序列值作为密钥,而本方案中仅需要M+N个混沌序列值即可完成加密,这大大节省了混沌迭代所需时间开销。在加密后期还采取整行方式进行操作,无需逐个像素进行加密,这很大地提高了算法加密速度,因此整个算法执行效率较高。
5 结束语
本文介绍了一种基于超混沌的自适应图像加密算法。该算法先是根据原始像素信息对密钥序列进行改造处理,建立了密钥与明文图像的关联性。然后通过前一密文像素与密钥值进行非线性变换产生中间密钥,利用中间密钥对各个像素采取自适应加密策略进行加密操作。这种方法不仅节省了密钥长度与加密时间开销,而且具有更好的密钥敏感性。实验结果表明,该算法安全高效,在军事、信息存储、信息传输等实际应用中具有较大前景。
[1] Wei Jun,Liao Xiaofeng,Wong Kwok-wo,et al.Cryptanalysis of a cryptosystem using multiple one-dimensional chaotic maps[J].Communications in Nonlinear Science and Numerical Simulation,2007,12(5):814-822.
[2] Wang Xingyuan,Wang Xiaojuan,Zhao Jianfeng,et al.Chaotic encryption algorithm based on alternant of stream cipher and block cipher[J].Nonlinear Dynamics,2011,63(4):587-597.
[3] He Jun,Qian Haifeng,Zhou Yuan,et al.Cryptanalysis and improvement of a block cipher based on multiple chaotic systems[J].Mathematical Problems in Engineering,2010,2010:Article ID 590590.
[4] 王继志,王英龙,王美琴.一类基于混沌映射构造Hash函数方法的碰撞缺陷[J].物理学报,2006,55(10):5048-5054.
[5] Liu Shubo,Sun Jing,Xu Zhengquan,et al.Digital chaotic sequence generator based on coupled chaotic systems[J].Chinese Physics B,2009,18(12):5219-5227.
[6] Gao Tiegang,Chen Zengqiang.A new image encryption algorithm based on hyper-chaos[J].Physics Letters A,2008,372(4):394-400.
[7] Rhouma R,Belghith S.Cryptanalysis of a new image encryption algorithm based on hyper-chaos[J].Physics Letters A,2008,372(38):5973-5978.
[8] 王静,蒋国平.一种超混沌图像加密算法的安全性分析及其改进[J].物理学报,2011,60(6):83-93.
[9] 卢辉斌,孙艳.基于新的超混沌系统的图像加密方案[J].计算机科学,2011,38(6):149-152.
[10] 朱从旭,孙克辉.对一类超混沌图像加密算法的密码分析与改进[J].物理学报,2012,61(12):76-87.
[11] 钟厚桥,李建民,林振荣,等.基于超混沌序列的图像加密方案[J].计算机应用研究,2013,30(10):3110-3113.
[12] Wang Haoxiang,Cai Guoliang,Miao Sheng,et al.Nonlinear feedback control of a novel hyperchaotic system and its circuit implementation[J].Chinese Physics B,2010,19(3):154-161.
[13]李玲,王伟男,李津杰,等.基于Logistic映射和超混沌的自适应图像加密算法[J].微电子学与计算机,2012,29(1):42-46.
[14] 柏森,胡中豫,吴乐华,等.通信信息隐匿技术[M].北京:国防工业出版社,2006.
[15] 朱从旭,胡玉平,孙克辉.基于超混沌系统和密文交错扩散的图像加密新算法[J].电子与信息学报,2012,34(7):1735-1743.
[16] Teng Lin,Wang Xingyuan.A bit-level image encryption algorithm based on spatiotemporal chaotic system and selfadaptive[J].Optics Communications,2012,285(8):4048-4054.
[17] Zhu Zhiliang,Zhang Wei,Wong Kwok-wo,et al.A chaosbased symmetric image encryption scheme using a bit-level permutation[J].Information Sciences,2011,181(6):1171-1186.
