基于MPI的并行密码恢复框架

蒋璐瑾

(湖南省妇幼保健院信息中心，湖南 长沙 410011)

0 引言

密码是保护保密数据的重要手段，对称密钥加解密算法虽然安全度不高，但是具有使用方便的优点。因此，对称密钥加解密方法至今仍然被广泛使用。用户可以将数据用一个密钥进行处理，并把加密后的数据发送到接收端，在接收端用户再用同样的密钥解密。如果加密数据在传输过程被获取，解密方在不知道加密密钥的情况下，需要通过几百万次、甚至几百万亿次的尝试才可能破解密码，此种方法也称为“暴力破解”。在没有任何密码破解提示的情况，使用当前的单机系统，很难在有限时间内破解一个加密文件。

基于字典(Dictionary-based Password Recovery)的密码破解技术[1-4]通过尝试一个密码字典中的所有密码来破解加密数据。密码字典通常由熟悉的名称、常用单词、简单字符序列等组成，针对由大量密码组成的密码字典，顺序地测试每个密码是一种很费时的工作。但是，此类计算具有天然的并行性，因为各个密码的测试是相互独立的，这些测试可以并行执行。因此基于字典的密码恢复技术易于被高性能计算机并行执行。

一个大的密码字典通常会提高破解密码的可能性。但是，这也提高了计算复杂性。基于用户密码的可能概率分布，Weir[2]设计了一个自动生成字典的系统。基于特殊字符和数字出现的概率，该系统首先分析训练密码集合，从而决定生成密码的不同语法的概率。此方法可以根据已知的密码集合，分析出密码生成的概率，从而派生出可能的未知密码集合。生成的密码集合以预测的可能性的概率从高到低排序。JtR[5]是一个开源的软件包，该软件包设计的目的是破解具有特殊格式的密码，例如基于MD5和SHA-1的加密密码。这个工具对于恢复忘记的密码和弱密码很有用。此外JtR还支持基于字典的攻击。马尔科夫链也可以用来进行数据解密[6]，某些情况下性能优于JtR和暴力破解。在实际应用过程中，马尔科夫过程比JtR更有效果。马尔科夫过程的另一个突出的优点是它可以在一个确定的时间完成。

在高性能计算领域，有很多基于MPI(Message Passing Interface，消息传递接口)或OpenMPI的工具集[7-15]。Foster[16]首 先 提 出 了 网 格 计 算 技 术，MPICHG是一种基于网格的MPI实现。基于分布式提供的志愿计算资源，Bernaschi[4]设计了一种面向松耦合系统结构的密码破解框架。该框架把异构的节点分为不同类型节点，第1层是根节点，第2层和第3层是计算节点，不同层次的计算节点的功能不同。Pellicer[17]基于 BOINC 系统结构，设计了一种面向MD4算法的密码搜索算法。

本文设计并实现了一个基于MPI的并行密码恢复框架P2RF(Parallel Password Recovery Framework)。该框架把需要解密的数据和候选密钥在任务级分布到不同的计算节点上，计算节点再根据节点计算资源配置的不同把计算分布到计算资源上。本文使用多种实验测试集分析了P2RF的内存占用和执行时间情况，针对不同的测试集合分析了其任务分布和内存占用的策略。

1 P2RF框架的设计与实现

1.1 框架设计

P2RF框架由3部分组成:根节点、计算节点、字典文件，如图1所示。根节点和计算节点集合可以是独立的物理节点也可以是网格上的虚拟节点，字典文件存储在文件系统中，可以在本地磁盘中也可以在磁盘阵列中。

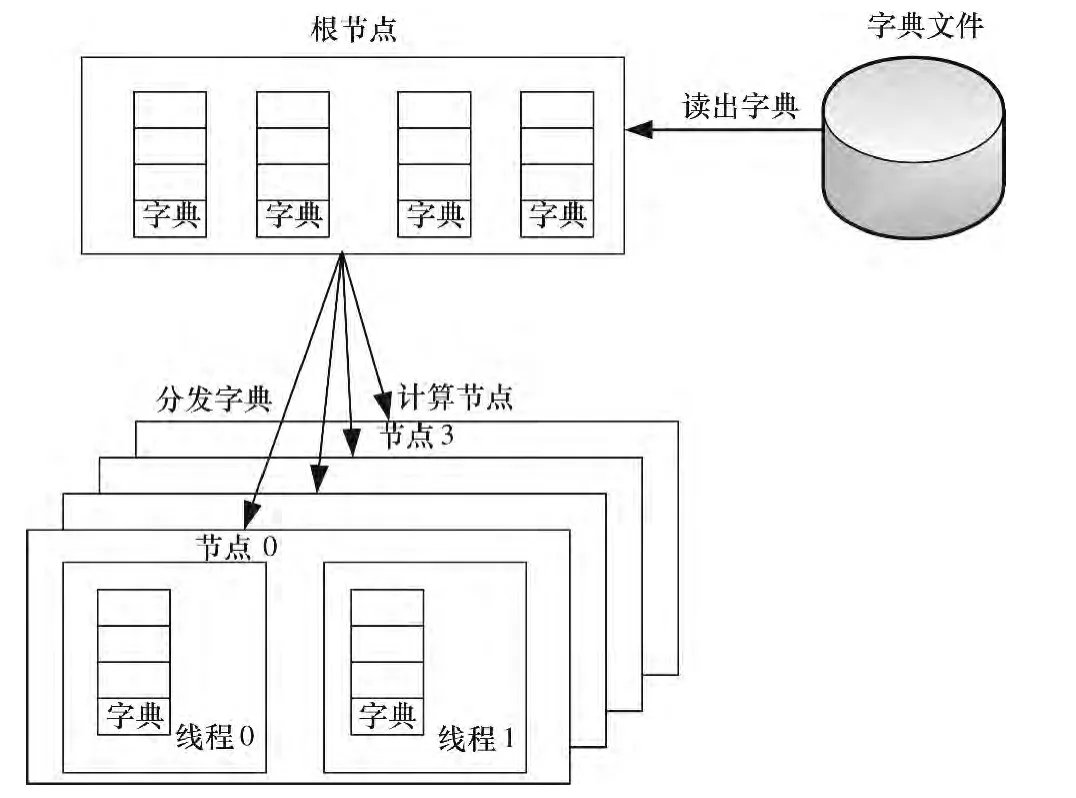
图1 P2RF框架设计

加密数据破解的基本步骤为:

1)把密码字典和加密数据分布到不同的节点;

2)每个节点根据分布到自己的密码字典，解密加密数据，通过CRC校验判断密码的有效性;

3)如果发现正确的密码，则程序停止并报告。

根节点的功能是从字典文件中读取字典，然后派发到计算节点，根节点读取是采用非阻塞读取的方式，把字典文件中的数据分批读入到根节点的主存中，根节点再把数据以非阻塞的方式发送到计算节点。因此，根节点开辟了多块缓冲区，这些缓冲区顺序地被字典文件数据填满，当数据被发送到计算节点后，缓冲区被标记为空闲，等待下次被字典文件数据填满。

计算节点使用双缓冲从根节点接收字典数据，当缓冲数据到达后，把数据发派到计算线程或加速器上(这些都称为可执行部件Process Element，PE)，这些可执行部件根据收到的字典密钥，进行对加密数据的解密操作，通过比较校验和判断该密钥是否为正确的密钥，当计算节点找到了正确的密钥，就把正确的密钥报告给根节点，此时，根节点发送结束通知信息给所有的计算节点。如果一个计算节点尝试了所有的密钥都没有找到正确的密钥，则发送请求给根节点，让根节点发送新的字典给自己。如果一个计算节点在测试本次的密钥集合过程中，收到了根节点已经寻找到正确密钥的通知，则该计算节点等待当前密钥的判断结束后，立即退出程序。

1.2 框架实现

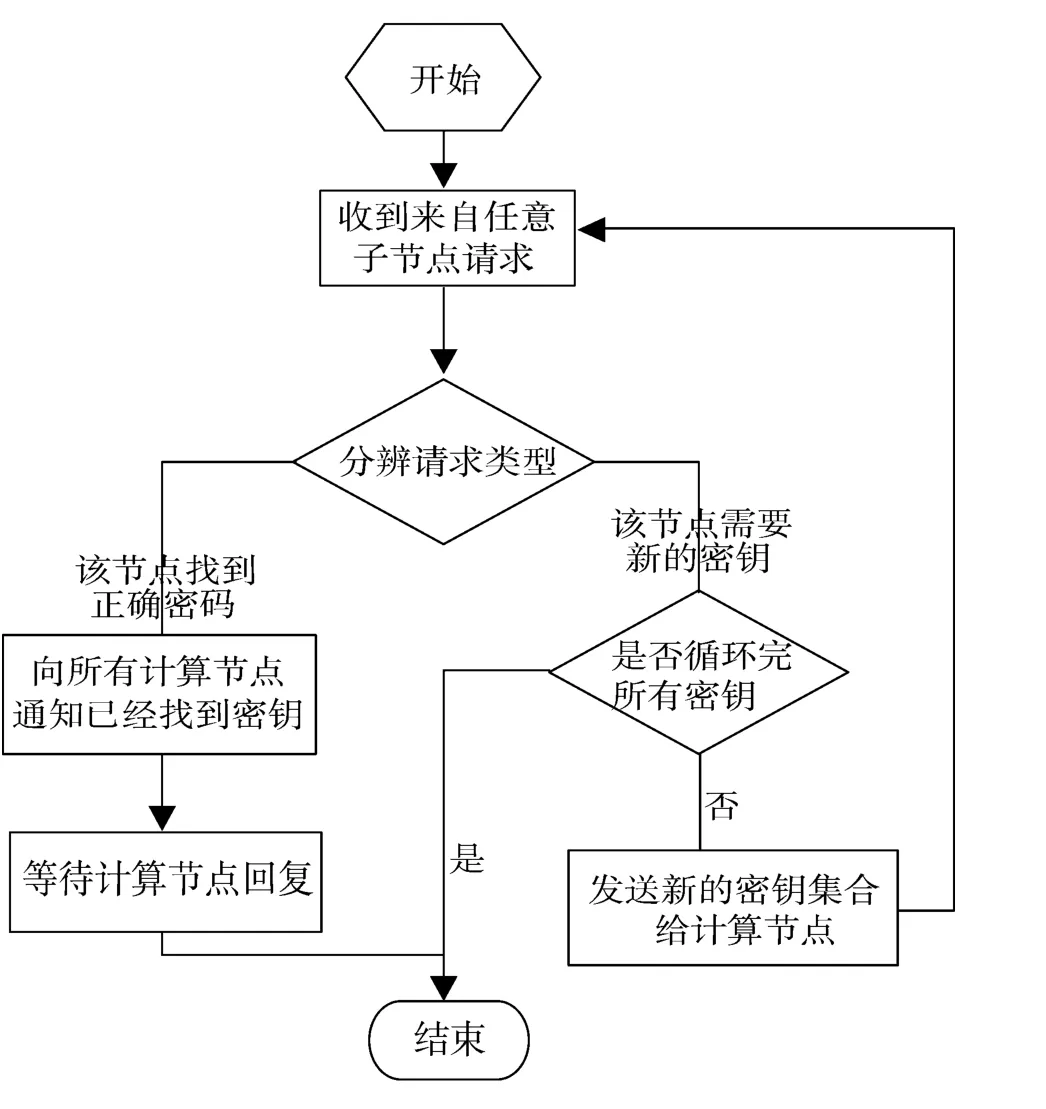
图2 P2RF框架根节点功能实现

框架包括2个部分:根节点的实现和计算节点的实现，根节点和计算节点间的通信采用MPI通信库实现。图2给出了根节点的功能实现，系统初始化后，根节点处于等待状态，等待计算节点发送的请求，如果计算节点计算完成当前需要处理的密钥，则向根节点发出请求，如果根节点发现字典已经处理完成，则说明当前字典没有找到正确的密钥，那么就向计算节点发送计算完成的指令，计算节点收到该指令后即退出;如果仍然有没有处理完成的密钥，则继续发送密钥给计算节点，计算节点收到密钥后，解密这批密钥的正确性;如果一个计算节点找到了正确的密钥，则发通知给根节点，根节点收到通知后，会等待没有完成的计算节点，当计算节点发送下一阶段的请求后，则通知它计算已经完成，找到了正确的密钥。

1.3 任务调度模块

在并行程序执行过程中，任务调度的作用是控制循环并行结构的执行。P2RF框架专门设计了调度模块，可以通过调度去控制解密任务的调度和分配，从而适应不同的使用情况，提高性能。P2RF框架的调度模块支持3种工作模式:静态调度、动态调度和用户指导的调度。

1)静态调度。

系统默认采用的是静态调度方式。静态调度的关键输入参数为chunk，表示一个线程执行的默认子任务数目(需要解密的密码空间)，当需要执行的子任务数目为 N，执行计算的线程数为 M时，[0，chunk-1]的chunk次的迭代是在第1个线程上运行，[chunk，2*chunk-1]是在第2个线程上运行，依次类推。该任务分配过程是静态确定的，不会因为运行的情况改变。如果chunk没有指定，只是指定采用静态类型，那么系统使用子任务数/线程数作为chunk的值，这样每个线程执行的子任务数目就是一样的。

2)动态调度。

动态调度的子任务分配是依赖于运行状态动态确定的，所以哪个线程上将会运行哪些子任务是无法像静态调度一样事先预料的。对于动态调度，没有chunk参数的情况下，每个线程按先执行完先分配的方式执行Iter个子任务，比如，刚开始，线程1先启动，那么会为线程1分配Iter个子任务开始去执行，然后，可能线程2启动了，那么为线程2分配Iter个子任务，假设这时候线程0和线程3没有执行完，而线程1的子任务已经执行完，可能会继续为线程1分配Iter个子任务。所以，动态分配的结果是无法事先知道的，这些都是取决于系统的资源、线程的调度等。

3)用户指导的调度。

用户指导的调度类似于动态调度，但每次分配的子任务数目不同，开始分配的数目比较大，以后逐渐减小。chunk表示每次分配的子任务数目的最小值，由于每次分配的子任务数目会逐渐减少，当减少到chunk时，分配的子任务数目将不再减少。

运行过程中，程序员可以通过设置 P2RF_SCHED_TYPE环境变量，来配置任务调度策略，其语法是 export P2RF_SCHED_TYPE=“type，chunk”。其中，type 可以是 static、dynamic、guided，chunk 可以选择设置为正整数。

2 实验结果和分析

为了验证P2RF框架的有效性，在表1所示平台上测试了P2RF框架的性能，测试用例采用大小为16 kB的加密Word文档。该平台的每个计算节点有2个CPU，每个CPU有6个计算核心，每个计算节点有12个核。

表1 实验平台介绍

实验结果如图3所示，本实验的调度策略是static，chunk=2048。从图3可知，系统平均每秒的解密次数随着计算节点数目的增加近似线性增长(根节点不参与计算过程)，例如2个节点的时候，框架的解密能力是11850次/s，32个节点的时候，系统解密能力是365000次/s。可见系统的扩展性是线性可扩展的。

为了分析解密数据大小对解密速率的影响，在32节点的平台上，使用不同大小的解密数据测试了P2RF的解密速率。实验结果如图4所示，当解密数据规模为128 kB时，解密速率可达68万次，基本上为数据规模为256 kB时的2倍，这说明2点:首先，P2RF框架的并行效率较好，通信不会引入冗余的开销;其次，P2RF选择的串行解密算法的计算复杂度是O(N)量级的，其运算时间和被解密数据的大小正相关。但是，当数据规模逐渐变大时，例如在4096 kB时，解密速率只有2万6千次，这是因为最后一级共享Cache不能容纳所有线程的访存工作集合，出现了一定的Cache失效，导致了系统性能的下降。

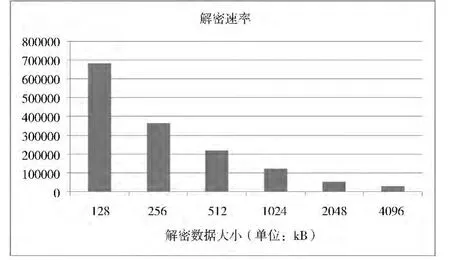
图4 P2RF框架解密速率分析图

3 结束语

本文设计了一个基于MPI的并行密码恢复框架P2RF，该框架把需要解密的数据和候选密钥在任务级分布到不同的计算节点上，计算节点再根据节点计算资源配置的不同把计算分布到计算资源上。实验结果表明:P2RF的扩展性随着节点的增多而线性扩展。

[1] Grama A，Karypis G，Kumar V，et al Introduction to Parallel Computing[M].2nd Edition.Addison Wesley，2003.

[2] Weir M，Aggarwal S，de Medeiros B，et al.Password cracking using probabilistic context-free grammars[C]//Proceedings of the 30th IEEE Symposium on Security and Privacy.2009:391-405.

[3] Dell’Amico M，Michiardi P，Roudier Y.Password strength:An empirical analysis[C]//Proceedings of the 29th IEEE Conference on Computer Communications.2010:1-9.

[4] Bernaschi M，Bisson M，Gabrielli E，et al.An architecture for distributed dictionary attacks to cryptosystems[J].Journal of Computers，2009，4(5):378-386.

[5] Peslyak A.John the Ripper[DB/OL].http://www.openwall.com/john/，2013-05-30.

[6] Marechal S.Advances in password cracking[J].Journal in Computer Virology，2008，4(1):73-81.

[7] 张华杰.基于MPI的并行算法的研究[D].金华:浙江师范大学，2010.

[8] Wilkinson B，Allen M.并行程序设计[M].陆鑫达，等译.北京:机械工业出版社，2005.

[9] Li Kuan-Ching，Chang Hsun-Chang，Yang Chao-Tung，et al.On construction of a visualization toolkit for MPI parallel programs in cluster environments[C]//Proceedings of the 9th International Conference on Advanced Information Networking and Applications.2005，2:211-214.

[10] Panda D K，Ni L M.Special issue on workstation clusters and network-based computing[J].Journal of Parallel and Distributed Computing，1997，40(1):1-3.

[11] Desai N，Bradshaw R，Lusk A，et al.MPI cluster system software[C]//Proceedings of the 11th European PVM/MPI Users’Group Meeting.2004:277-286.

[12] 都志辉.高性能计算并行编程技术:MPI并行程序设计[M].北京:清华大学出版社，2001.

[13] Chong Yong-Kim，Hwang Kai.Performance analysis for four memory consistency models for multithreaded multiprocessors[J].IEEE Transactions on Parallel and Distributed Systems，1995，6(10):1085-1099.

[14] Hockney R W.The Science of Computer Benchmarking[Z].The Society for Industrial and Applied Mathematics，Philadelphia，1996.

[15] 李继民，马力，王风先.PC机群系统的关键技术[J].河北大学学报(自然科学版)，2002，22(1):55-58.

[16] Foster I，Karonis N T.A grid-enabled MPI:Message passing in heterogeneous distributed computing systems[C]//Proceedings of the 1998 ACM/IEEE Conference on Supercomputing.1998.

[17] Pellicer S，Pan Yi，Guo Minyi.Distributed MD4 password hashing with grid computing package BOINC[C]//Proceedings of the 3rd International Conference on Grid and Cooperative Computing.2004:679-686.