基于突变决策方法的物流虚拟企业选择研究

张云丰，王 勇，龚本刚，桂云苗

（1.安徽工程大学 管理工程学院，安徽 芜湖 241000；2.重庆大学 经济与工商管理学院，重庆 400030）

近年来，国内外学者对虚拟企业合作伙伴选择问题进行了大量研究，并取得丰富的研究成果［1－6］.部分学者结合虚拟企业的特点和物流行业的特殊性，提出了针对物流虚拟企业合作伙伴选择的新思路［7－10］.物流虚拟企业合作伙伴选择属于典型的多属性决策问题，基于各属性对决策目标的贡献不同，在评价时需要给各属性分配相应的权重，而权重的分布将很大程度上制约着最终方案的排序.确定属性权重的方法有主观赋权法和客观赋权法，前者如层析分析法、Delphi法、二项系数法、环比评分法等；后者如最大熵技术法、主成分分析法、变异系数法、离差最大化法等.主观赋权法主要依靠决策者的经验、知识等主观因素来确定，片面性太强；而客观赋权法需要掌握属性的大量信息，可操作性又较差.因此，在多属性决策问题中，若能寻找到一种避免确定属性权重的评价方法，那么必然使得排序结果更具有说服力.突变决策方法作为多属性评价决策的一种管理技术，能够很好地满足此要求.目前这种方法在交通流预测、生态环境评估、灾害诊断及众多社会科学领域都得到了广泛应用，尤其适用于解决属性权重难以量化的多属性决策和矛盾目标决策问题.

1 基于突变决策方法的多属性决策机理

1.1 突变模型的基本原理

突变模型是由数学家R.Thom创立的一种综合应用拓扑学、奇点理论和结构稳定性等数学工具研究系统行为演变非连续现象的决策方法.突变模型的研究对象是系统的势函数，势函数（f（x））是描述系统的状态变量和控制变量之间相对关系、相对位置的函数.令f′（x）＝0可以得到该系统所有临界点集合成的平衡曲面方程，该平衡曲面的奇点集可以通过令f″（x）＝0获得.由f′（x）＝0和f″（x）＝0消去x，则得到由状态变量表示的反映各状态变量与各控制变量间分解形式的分歧点集方程.系统的所有性质都由分歧点集方程决定，当各控制变量的变化不满足该方程时，系统只有量的改变；一旦满足该方程，系统将出现质的改变.从系统的势函数和分歧点集方程出发，可以推导突变模型的归一公式.归一公式是利用突变模型进行决策的基本运算公式，它将系统内部各属性的不同质态归化为可比较的同一质态，从而对系统进行量化递归运算，求出表征系统状态特征的系统总突变隶属函数值，作为系统综合评价的依据.

1.2 突变模型的多属性决策思路

假定某一个多属性决策系统在任何时刻的状态特征X可完全由有限的变量xi＝（x1，x2，…，xm）（i＝1，2，…，m）的值来确定，而变量xi又受变量xij＝（xi1，xi2，…，xin）（j＝1，2，…，n）的控制，即变量xij的值决定了变量xi的值.我们把变量xi称为系统的内在变量，变量xij称为系统的外在变量，由此建立多属性决策系统综合评价的属性递阶层次结构模型（见图1）.如果我们把多属性决策系统里的每一个属性看成是由其相应下层属性的行为变化所决定的状态变量，就可以借助突变模型来研究下层属性（称为控制变量）对上层属性（称为状态变量）的作用机制.简单地说，若一个属性受若干个下层属性的行为变化所控制，则将其视为发生相应突变行为的状态变量.

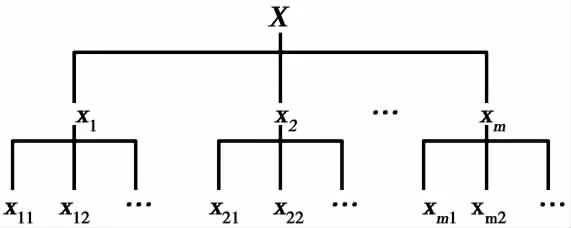
图1 属性递阶层次结构模型

当建立起属性递阶层次结构模型后，在已知最底层属性数值的情况下，通过转换公式将不同物理量纲的属性数据做规范化处理，利用各种突变模型的归一公式逐步将下层属性的取值转化为相应的上层属性评价参数，即确定下层属性对上层属性的突变隶属函数值，最终求得多属性决策系统总突变隶属函数值，对各总突变隶属函数值排序后便可进行决策.

2 物流虚拟企业选择基本步骤

结合突变模型的多属性决策思路，归纳出突变决策方法进行物流虚拟企业选择的基本步骤如下：

第1步 按照物流虚拟组织的内在作用机理，将决定其状态特征的变量分解成由多个属性组成的多层系统，建立多属性决策系统的递阶层次结构模型.在模型示意图里，一般将主要控制变量写在前面，次要控制变量写在后面.

建立物流虚拟企业属性递阶层次结构模型时，一般需遵循以下原则：①快速响应原则.物流虚拟企业的特点就是对市场机遇作出快速反应，因此要求合作伙伴具有较高的敏捷性，对市场机遇或虚拟企业内部的请求具有快速反应能力；②效益增加原则.效益增加体现在两个方面：一是组建物流虚拟企业使得资源得到了整合，产生了更强的竞争力，获得更大的收益；二是整合后总的交易费用和管理费用比原先各自的费用和要小；③核心能力互补原则.组建物流虚拟企业的目的就是要用非核心企业的优势去弥补核心企业的劣势，达到强强联合，提高虚拟企业整合的效果；④风险弱化原则.市场风险是不可避免的，但可以分散，组建物流虚拟企业可以在一定程度上回避或分散物流虚拟企业整体的运行风险，使整体风险最小化.

对多个控制变量进行主次排序时，多位决策专家的评价结果可能不一致，可以通过计算平均Spearman等级相关系数来作出选择.设D位决策专家分别对n个控制变量给出一组排序，di表示两位决策专家排序结果的差值，则决策专家p和q之间的Spearman等级相关系数为：

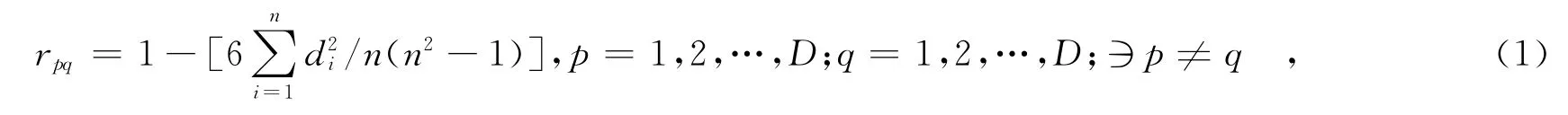
对rpq加权求和，得到决策专家p的平均Spearman等级相关系数表达式：

令rk＝max｛rp｜p＝1，2，…，D｝，则认为决策专家k的评价结果与其他决策专家的评价结果一致性最好，可以作为控制变量的最优排序.当样本容量超过20时，必须对Spearman等级相关系数进行显著性检验.由于初等突变模型里涉及的控制变量个数远小于20，因此不需要再进行显著性检验.

第2步 获取最底层属性原始数值（控制变量），应用转换公式对其进行规范化处理，得到0～1区间内的越大越优型无量纲可比较数值，即最底层属性初始的隶属函数值.

在获取最底层属性原始数值时，经常会遇到部分属性值难以量化的困难.其原因在于有些属性是定性类的，受制于人类思维的模糊性及受专业知识水平等客观因素的影响，很难用精确的实数值来量化.相反，采用模糊类语言变量来刻画它们则显得更贴近实际.

为了应用模糊类语言变量来刻画属性的评估信息，在此引入不确定语言评估标度［11］.设S＝｛sa｜a＝－L，…，L｝为不确定语言评估标度，其中sa表示不确定语言变量，s－L和sL分别表示不确定语言变量的下限和上限，且满足下列性质：①若a＞b，则sa＞sb；②存在负算子neg（sa）.S中不确定语言变量根据实际需要进行标度，但一般取奇数个，如取S＝｛s－5，…，s5｝＝｛极差，很差，差，较差，稍差，一般，稍好，较好，好，很好，极好｝.如果γ＝［sα，sβ］，其中sα，sβ∈S且α ≤β，则称γ为不确定语言区间数.

在不确定语言属性信息集成过程中，为了避免决策信息丢失和方便计算，在原有标度S基础上定义一个拓展标度¯S＝｛sa｜a∈［－N，N］｝，其中N（NØL）是一个充分大的自然数，且若a∈｛－L，…，L｝，则称sa为本原术语；若a∉｛－L，…，L｝，则称sa为拓展术语.通常，决策专家标度属性值时使用本原术语，拓展术语只出现在运算和排序过程中.

为方便决策时对不确定语言变量进行转化和比较，可运用以下不确定语言评估标度的度量公式：

定义1 在不确定语言评估标度中，对任意两个不确定语言区间数μ＝［sa，sb］∈~S，v＝［sc，sd］∈~S，令κ，κ1，κ2∈ ［0，1］，满足下列运算法则：

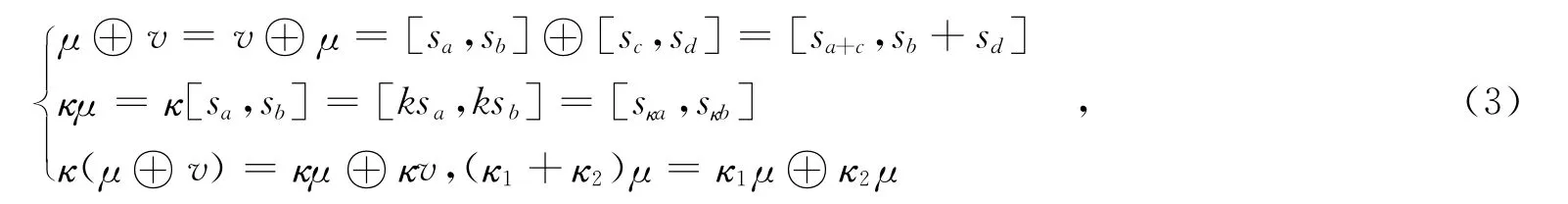
定义2 在不确定语言评估标度中，对任意两个不确定语言区间数μ＝［sa，sb］∈~S，v＝［sc，sd］∈令lengthab＝b－a，lengthcd＝d－c，，则μ≥v的可能度为：

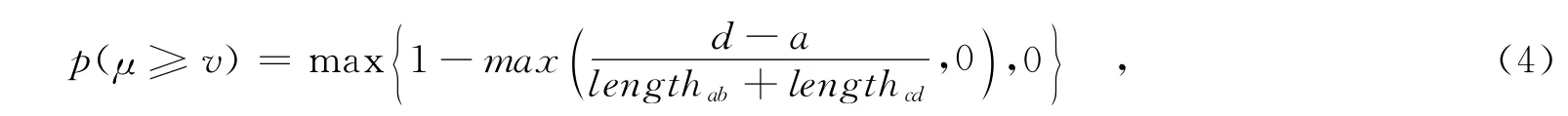
显然，v≥μ的可能度p（v≥μ）＝1－p（μ≥v）.

定义3［12］设P＝（pij）m×m为决策专家对所有方案的第i个属性赋予的不确定语言区间数转化后的可能度矩阵，则可能度矩阵P的排序向量计算公式为：

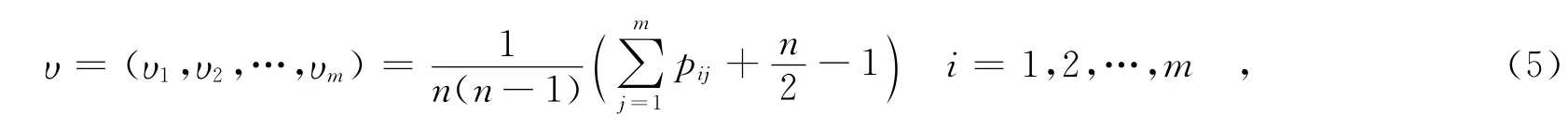
第3步 根据状态变量所属控制变量的个数，确定物流虚拟企业选择多属性决策系统各层次的突变模型种类，依据相应的归一公式进行逐层量化递归运算，得到每一物流虚拟企业的总突变隶属函数值.

数学上已经证明，当状态变量不多于2个、控制变量不多于5个时，自然界的各种突变最多可有11种形式，且又以1个状态变量的5种初等突变模型应用最为广泛，如表1所示.其中，x为系统的状态变量（上层属性），f（x）为状态变量x的势函数，a～e为状态变量x的控制变量（下层属性）.

表1 常用5种初等突变模型

对n个控制变量的各种突变模型的势函数分别求n阶导数，令其表达式等于零，则可确定相应的分歧点集方程与归一化公式，以燕尾突变为例：

解得a＝－15x4，b＝20x3，c＝－10x2，用t1＝－a/15，t2＝b/20，t3＝－c/10进行替换，有再将原变量换回即为归一化公式.常用5种初等突变模型的分歧点集方程与归一化公式如表2所示.

按归一公式计算系统状态变量时，若一个系统的诸控制变量间没有互补关系，应从诸控制变量相应的突变隶属函数值中选最小值作为系统的状态变量值，即x＝min｛x（a），x（b），…｝；相反，若存在互补关系，则应选诸控制变量的突变隶属函数值的平均值作为系统的状态变量值，即x＝aver｛x（a），x（b），…｝.

第4步 对得到的各物流虚拟企业总突变隶属函数值进行大小排序，作出综合决策.由于总突变隶属函数值属于0～1区间内的越大越优型无量纲数值，可直接进行比较，因此，决策者只需选择总突变隶属函数值最大的物流虚拟企业即可.

表2 分歧点集方程与归一化公式

3 算例分析

某第四方物流企业为实现某一物流机遇欲在市场寻求第三方物流企业组建动态物流联盟，经过初步筛选，确定3家第三方物流企业作为候选对象.第四方物流企业依据有关原则，并结合物流虚拟企业的特点，准备建立包含5个一级属性、13个二级属性的属性递阶层次结构模型.现需对5个一级属性及所属二级属性进行主次排序.5位决策专家对5个一级属性给出的主次排序结果如表3所示.

表3 一级属性初始主次排序表

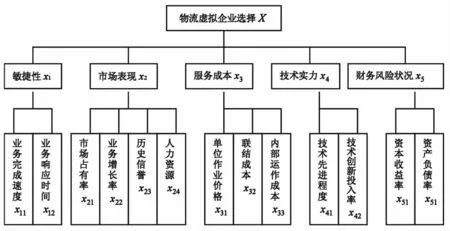
图2 物流虚拟企业选择属性递阶层次结构模型

根据Spearman等级相关系数计算公式，有r1＝0.838，r2＝r4＝0.850，r3＝0.688，r5＝0.700.因此，决策专家D2和D4的排序结果最优.同理可计算出各二级属性的平均Spearman等级相关系数.最终建立物流虚拟企业选择的属性递阶层次结构模型如图2所示.

决策专家们对获取的信息综合分析并经多轮协商后，赋予各二级属性原始不确定语言区间数，运用式（3）～（5）对原始数据进行规范化处理，得到最底层属性初始隶属函数值，两组数据如表4所示.

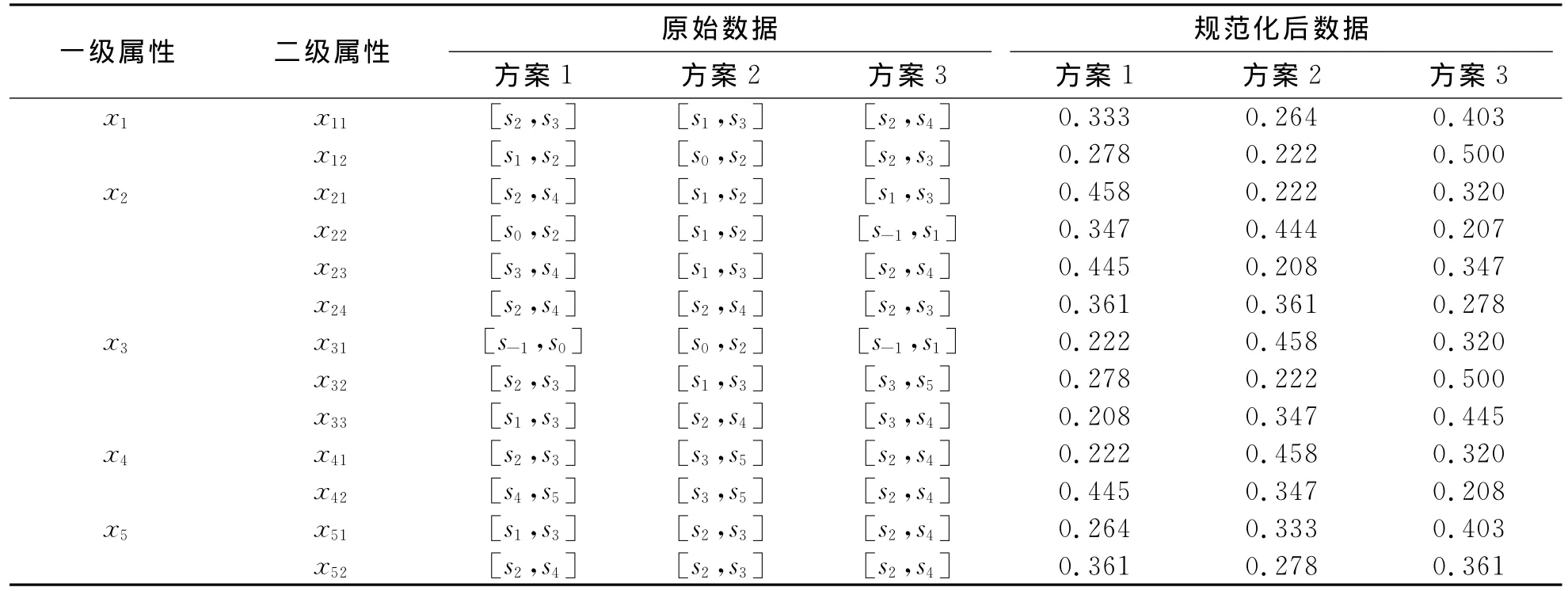
表4 二级属性不确定语言评估数据

图3 物流虚拟企业选择的递阶突变模型

根据突变模型种类，结合属性递阶层次结构模型，可得出虚拟物流企业选择的递阶突变模型，如图3所示.其中，控制变量（x1，x2，x3，x4，x5）、控制变量（x21，x22，x23，x24）、控制变量（x31，x32，x33）、控制变量（x51，x52）为非互补型，应从突变隶属函数值中取小；控制变量（x11，x12）、控制变量（x41，x42）为互补型，应取突变隶属函数值的平均值.

结合物流虚拟企业选择的递级突变模型和突变隶属函数值取值原则，利用归一公式由下向上逐层计算，直到得出最高层的总突变隶属函数值.由于计算过程简单且工作量较大，下面仅以一级属性市场表现的突变隶属函数值的计算过程为例.

按照“非互补”取值原则，3个方案的突变隶属函数值分别为0.677、0.471、0.566.同理，可计算出其他一级属性及系统总突变隶属函数值，如表4所示.从表4给出的计算结果可以看出，3个方案的优劣次序为X3＞X1＞X2＞，因此，第三方物流企业X3是组建动态物流联盟的最佳合作伙伴.

表4 一级属性突变隶属函数值及总突变隶属函数值

4 小结

本文研究了如何运用突变决策方法进行复杂系统多属性决策，并以物流虚拟企业选择为例说明整个决策过程.突变决策方法的优势在于，可以避免确定属性权重的问题，它将属性对决策目标的重要程度转化为由归一公式的内在机理决定.应用突变决策方法进行虚拟物流企业选择时，需要解决一个关键问题，即同级别的属性主次排序.属性的排序结果对最终方案的排序产生重要影响，排序结果的合理与否关系到突变决策方法本身是否科学.现有文献尚未涉足这一问题的研究.因此，引入平均Spearman等级相关系数来度量各排序结果间的一致性程度，取得了良好效果.另外，在刻画最底层原始属性值时，采用不确定语言评估标度，最大限度地避免了由于信息不完全、人类思维的模糊性及专业知识水平制约等因素造成的消极影响.最后的算例验证了突变决策方法的合理性，为多属性决策问题提供了一种新思路.

［1］ ZENG Zhi－Bin，LI Yan，ZHU Wen－xing.Partner selection with a due date constraint in virtual enterprises［J］.Applied Mathematics and Computation，2006，175（2）：1 353－1 365.

［2］ DENG Hong，CHENG Li，WANG Cheng－tao，et al.Multilevel manufacturing system of virtual enterprise based on manufacturing grid and strategies for member enterprise selection and task assignment［J］.Digital Object Identifier，2008，12（4）：330－338.

［3］ YE Fei，Li Yi－na.Group multi－attribute decision model to partner selection in the formation of virtual enterprises under incomplete information［J］.Expert System with Application，2009，36（5）：9 350－9 357.

［4］ 凌云，顾烨，魏贵义.动态联盟中伙伴选择的 Top－k问题的优化算法［J］.计算机集成制造系统，2010，16（3）：650－657.

［5］ 黄彬，高诚辉，陈亮.模糊完工时间和模糊交货期下的虚拟企业伙伴选择［J］.系统工程理论与实践，2010，30（6）：1 085－1 091.

［6］ 冯博，索玮岚.一种考虑维度表现权衡的虚拟企业伙伴信任评价方法［J］.系统工程，2011，29（12）：70－76.

［7］ 沈立新，陈燕.基于径向基函数网络的虚拟物流企业伙伴选择方法研究［J］.数学的实践与认识，2005，35（2）：43－49.

［8］ 沈立新，陈燕，徐颂，等.基于双层规划的虚拟物流企业伙伴选择［J］.软科学，2005，19（3）：30－33.

［9］ 岳意定，王雄.虚拟物流中心伙伴选择的不确定语言群体决策［J］.湖南大学学报：自然科学版，2008，35（3）：88－91.

［10］ 马跃如，王雄.多时段条件下动态物流联盟伙伴选择的模糊语言群体决策模型［J］.系统工程，2008，26（6）：32－36.

［11］ Xu Ze－shui.A direct approach to group decision making with uncertain additive linguistic preference relation［J］.Fuzzy Optimization and Decision Making，2006，5（1）：21－32.

［12］ 徐泽水.不确定多属性决策方法及应用［M］.北京：清华大学出版社，2004.