新型行星环锥齿轮功率分流式无级变速器的研究*

王 爽，董小瑞，毛虎平

(中北大学 机械与动力工程学院，太原 030051)

0 引言

无级变速器(CVT)可实现实时自主地改变传动比，达到发动机、变速器与汽车行驶道路载荷的最佳匹配，以满足车辆具有最优的动力性、燃油经济性和排放性能，而且汽车能够平稳变速，满足日益提高的乘坐舒适度。但传统的无级变速器传动效率不高，特别是其传动效率受车辆实时变化的工况影响较大［1］。另外，其传送带的使用寿命较短，变速范围较小，其应用推广相应的也受到一定的限制。故提出一种新型的行星环锥齿轮功率分流式无级变速器，即行星环锥齿轮式无级变速器和差动轮系的组合。是指在采用传统无级变速器的装置基础上，通过行星齿轮机构及其它组件的配置结构改进，添置压盘等机构，利用外部载荷实时正压力进行调控调速环和圆锥面之间的摩擦力，利用功率分流的方法，使其中一部分功率流经效率较低的行星架，另一部分功率流经行星环锥齿轮传动机构，这两部分功率在输出端汇合。由于行星锥齿轮的效率系数比行星架的传动系数高，从而在保证无级变速器本身传动优点的基础上，改善整个机构的传动效率。变速时，水平移动变速环，改变行星环锥齿轮的自转半径，实现变速;而且调速环和行星环锥齿轮是通过摩擦力传递动力的。其行星环锥齿轮调速范围大，传动效率高。在满负荷下可稳步从零起动，适应变工况工作。其中差动轮系组合真正实现功率分流，克服原行星环锥式无级变速器传递功率小的缺点［2］。因此在车辆等行业具有重要的实用价值意义。

1 传动结构与工作原理

该设计机构主要采用齿轮通过牵引力运动(实际为摩擦运动)，其效率在整个运动传动比变化范围内都比较高，其传动原理为:功率从输入轴7 输入，一部分功率直接传递到行星架11，另外一部分功率经过中心轮5、行星锥轮1、调速环2、中心齿轮21、行星齿轮20、中心内齿轮18、14 传递，两部分功率同时传递给行星齿轮13，行星轮将两部分功率进行合成，经过行星轮12、中心内齿轮9，最终通过输出轴10 将功率输出。调速时，改变外环2 和行星环锥齿轮1 自转半径，达到了无级变速的目的。不论在调速还是运转时，外环2 都不转动。输入轴7 的输入转矩以及输出轴10 的输出转矩为:

式中:P7—输入功率kW;n7—输入转速r/min。

图1 行星环锥齿轮功率分流式无级变速器机构简图

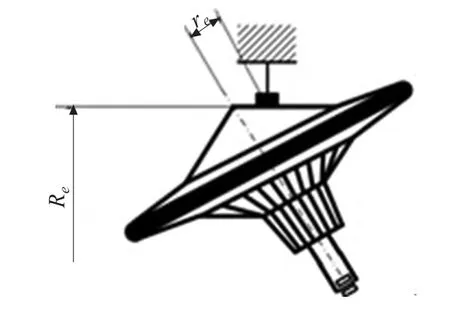
图2 行星环锥齿轮简图

对于环锥齿轮装置，由环锥大齿轮、环锥小齿轮和调速锥面结合传递动力。环锥齿轮没有保持架，处于浮动状态，在传递动力的三部分中，只有一部分是摩擦面，由此环锥齿轮浮动非常小，但是在工作状态下，特别是调速过程中，环锥齿轮存在倾翻力矩，使得其有一定的浮动量，从而降低传动效率，缩短环锥齿轮的寿命。为了改善此缺点，在环锥大齿轮和调速锥面之间设计一个圆环体，同时与其对应的小支撑环和大支撑环，这样可以平衡在调速过程中产生的倾翻力矩，不仅可以改善环锥大齿轮和环锥小齿轮的传动特性，而且可以提高调速环和调速锥面的寿命，减小滑动量，提高传递效率。

对于后续的差动轮系设计时，可能会出现两种情况，一种存在封闭功率流，另一种为功率分流传动。如果出现前者，不仅不能提高效率，反而封闭功率流使得效率减低，并且无级变速器的传递功率大大下降。该机构的差动轮系属于后者，属于完全功率分流传动。特点是输入功率大部分直接传递到行星架，而小部分功率经过环锥齿轮式无级变速器传递到内啮合中心轮，最后在行星轮处合成输出。

在机构设计装置中，合理选取行星环锥齿轮传动装置的结构参数和输入、输出构件的参数［3-4］，则是避免传动结构功率回流现象的关键，也是提高机构传动效率的有效途径。

2 传动比计算推导

由图一可知，从主动锥齿轮经过环锥齿轮至从动锥齿轮中，其机构的运动自由度为1，在后续的差动轮系中，其自由度为2;

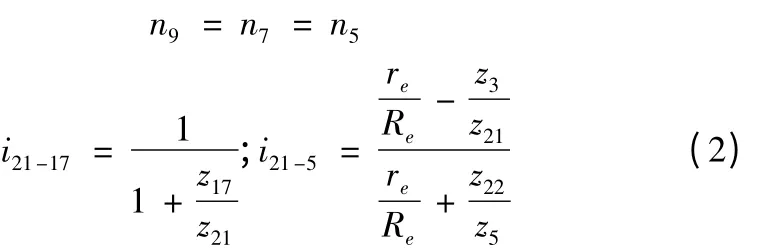
因此，我们也可以计算出来从输入轴到输出轴的总传动比为:

式中:i21、i21-5为中心内齿轮21 与齿轮17 的传动比、齿轮21 与齿轮5 的传动比。z17、z18、z3、z5、z21、z22、z13、z9、z12为中心齿轮17、齿轮18、齿轮3、齿轮5、齿轮21、齿轮22、齿轮13、齿轮9、齿轮12 的齿数;n9为输出中心轮的转速;n7为输入轴的转速;n5为主动中心锥齿轮转速。将图一简化为下图三，可以将差动轮系看作X，行星环锥齿轮轮系看作P。

图3 PX 封闭行星传动简图

由图一和图三可以计算出

由式子(1)、(3)、(4)可知:

则总传动比公式也可表示为:

式中:nt、nn、nu分别表示构件t、n、u的转速，nw表示输出轴端的转速;ithm表示差动轮系中固定构件t，当h主动，m从动时候的传动比［5-6］。

3 机构效率及功率的计算研究

3.1 分析功率能量流动的几种状况

在设计行星环锥齿轮轮系时，要特别注意轮系中的功率流动问题［7-10］。如其型式及有关参数选择不当时，可能会产生只在一般轮系内部循环流动的封闭功率流;依据PX 封闭行星传动简图可以得出一小部分功率通过输入轴和主动中心锥齿轮驱动行星环锥小齿轮，使各行星锥齿轮一方面随输入轴绕中心轴线作公转，同时本身在调速环的作用下又绕行星环锥齿轮自身的中心线作自转，二者合成的行星运动通过从动中心锥齿轮带动圆柱齿轮、同步齿轮、同步圆柱齿轮将功率传给定轴齿轮;然后，传给中心内齿轮及同步内啮合齿轮;同时大部分功率通过输入轴直接传给行星架;两部分功率通过行星轮合成，再经过同步行星轮、输出中心轮，最后总功率从输出轴输出。分析其PX 封闭行星环锥机构可知:如此可以增加机构系统的功率容量，以此提高机构的运转效率，从结构设计上避免复杂多变工况转换时系统的异常振动。

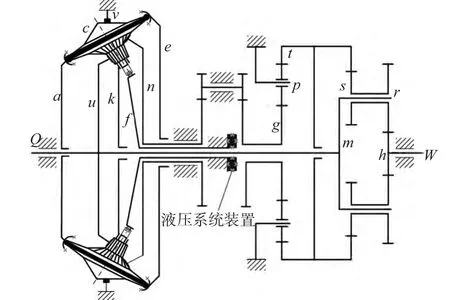
图4 图一与图三结合的结构简图

差动轮系和行星轮系以及谐波传动都可以看作三轴传动，其指具有三个基本构件的传动系统，且此三个基本构件的传动系统必须有三轴传动的内部结构形式和外部负载运动状况、工作条件共同决定的［11-12］。对于图3，由输入功率的流向及差动轮系和行星环锥齿轮无级变速器均为行星齿轮传动，满足力矩关系，则有下式成立:

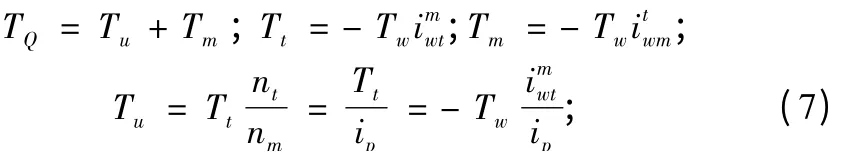
对于差动轮系传动组，则

对于行星环锥齿轮轮系传动组，则有

考虑到v为机架，相当于一轴输入，一轴输出，另一轴固定，输入功率等于输出功率。可得出行星环锥齿轮的功率分流式无级变速器机构的总比例

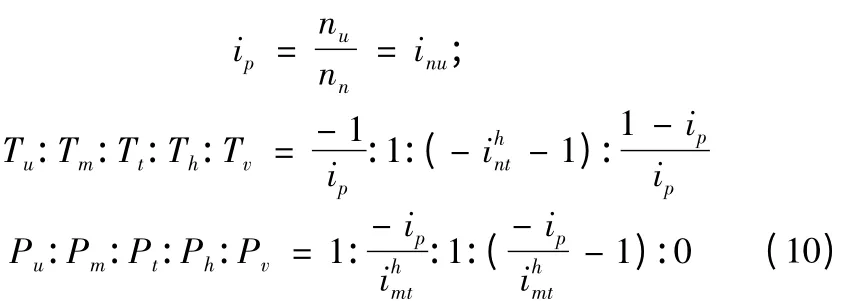
3.2 差动轮系效率的计算

式中:φ0=φ1+φ2+φ3;φ1、φ2为齿轮啮合损失的系数;φ3为轴承传动时的损失系数;φ0为总的轮系传动损失系数;在2K-H 差动轮系中，若m，t两轴输入，h轴端输出时，在考虑其能量损耗的前提下，输出轴动力及其传动的功率和传递的效率满足:

但当不考虑其能量损耗理想情况下功率之间的关系［8］:

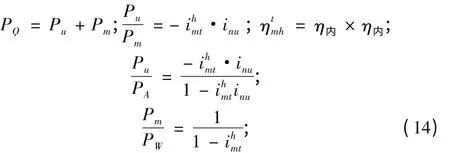
当行星轮的个数大于3 时，φ3=0.005，

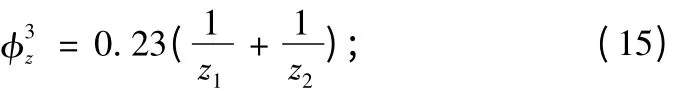
z1，z2为齿轮副中大、小齿轮的齿数。

ηtmh =η内×η内;，其他定轴轮系效率等数据均可查阅手册。

图5 原RX 环锥齿轮传动系

4 实验计算结果分析

以原2K-H 组合的功率分流式行星锥环无级变速器和本研究RX 行星环锥齿轮功率分流式无级变速器为研究比较对象，进行功率结果的分析比较。已知输入功率为2.2 kW，输入转速为1800r/min，齿轮啮合效率为η内=0.98;η外=0.99;图5 的与图4 中的取-0.5，令差动轮系中的传动比取不同值。计算分析步骤为:依据上式求出原行星环锥变速器效率即现行的效率、差动轮系的效率和定轴轮系的传动效率。最后可以求出其总效率。得到数据运用MATLAB 如图6 进行示意图分析比较:

图6 效率比较曲线

5 结论

(1)对RX 行星环锥齿轮功率分流式无级变速器适当调整其传动比，可以有效提高其工作传动效率;齿轮传动机构，行星环锥齿轮机构及其控制策略均满足车辆的操控性及平顺性的要求。

(2)两种RX 行星环锥齿轮功率分流式无级变速器均是随着传动比的增加而效率增加，但在较高速传动时，其总效率随着传动比增加降低。

该研究方法为进一步分析行星环锥齿轮功率分流式无级变速器机构传动过程、动力学分析、强度校核、优化设计分析等提供了较为准确可靠的依据。

［1］周祖焕. 齿轮无级变速原理［J］. 机械传动，2001(2):31 -33.

［2］赵玉香，孙首群，朱卫光，等.行星齿轮传动机构动力学分析［J］.机械传动，2008(4):69 -71.

［3］张兰春，常思勤.功率分流式无级变速器的整车经济性研究［J］.南京理工大学学报(自然科学版)，2008，32(3):346-349.

［4］罗绍新，王芙蓉.行星齿轮功率分流式无级变速器的设计研究［J］.机械设计与制造，2010(4):141 -143.

［5］胡强.新型无级变速器的设计与研究［D］. 武汉:武汉理工大学，2010.

［6］孙智民，沈允文，李素有.封闭行星齿轮传动系统的动态特性研究［J］.机械工程学报，2002，38(2):44 -48.

［7］毛虎平，任家骏.高效率功率分流式RX 行星环锥无级变速器研究［J］.机械管理开发，2007(3):1 -2.

［8］孙智民，季林红，沈允文.2K-H 行星齿轮传动非线性动力学［J］.清华大学学报(自然科学版)，2003，43(5):636-639.

［9］魏超，苑士华，胡纪缤.等差式液压机械无级变速器的速比控制理论与实验研究［J］.机械工程学报，2011，47(16):101-105.

［10］PFIFFNER R.GUZZELLA L，ONDER C H. Fuel—optimal control of CVT powertrains［J］. Control Engineering Practice，2003，11(3):329 -336.

［11］苑士华，侯国勇，张宝斌.液压机械无级变速器的变参数PID 控制［J］.机械工程学报，2004，40(7):81 -84.

［12］胡建军.金属带式无级变速传动系统速比匹配控制策略［J］.重庆大学学报，2001，24(6):12 -17.