高速铣削中刀具偏心跳动参数辨识

殷红梅，汪木兰，吴 玲

(1.淮安信息职业技术学院 机电工程系，江苏 淮安 223003;2.南京工程学院 先进数控技术江苏省高校重点建设实验室，南京 211167)

0 引言

在数控高速铣削中，铣削力作为评价铣削加工过程的一个重要物理参数，能够明显的反映加工状态过程的变化，与加工过程中的变形、振动和零件表面粗糙度有着密切的关系。目前国内外学者研究静态切削力模型较多，动态切削力研究较少，但在切削过程中，刀具偏心、跳动及刀具变形等都会直接影响瞬时未变形切削厚度的大小，进而影响加工零件的精度，同时刀具偏心对表面粗糙度和刀具寿命等的影响也不容小视［1］。因此，对刀具偏心跳动进行分析，建立包含刀具偏心跳动的铣削力模型显得尤为重要，本文即针对铣削中不可忽视的刀具偏心跳动展开研究，包括其宏观影响与微观算式，确定由其产生的瞬时铣削切削厚度以及综合瞬时铣削力中的偏心跳动参数，为高速铣削中铣削力模型的建立奠定基础。

1 刀具偏心跳动模型的建立

铣刀大部分为多刃铣刀，且为空间螺旋状，比较复杂，在制造过程中经常出现刀刃不对称或者偏心现象，同时受到刀柄和主轴锥孔接触刚度的影响，使得刀具回转中心与几何中心不重合，从而引起铣削过程中刀具的偏心跳动。偏心跳动一般可分为三种情况:第一种是刀具的回转中心平行偏离了刀具的几何中心;第二种是刀具的回转中心与刀具的几何中心在一平面内成一定的夹角;第三种是刀具的回转中心与刀具的几何中心成一定的空间夹角［2］。

刀具偏心跳动通常出现在多切削刃的铣削过程中，可以通过刀具偏心量和偏心角来表示。由于刀具偏心的存在，刀齿上任意切削微元切削的实际半径将会发生变化。在这里给出上述三种情形下实际半径的具体函数表达式［3］。

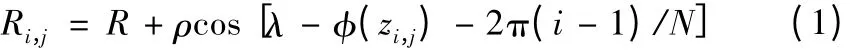
模型一:刀具的回转中心平行偏离了刀具的几何中心式中，Ri，j、R分别表示第i个刀齿上的第j个切削微元的实际切削半径和理想切削半径，ρ 为刀具偏心量，λ刀具偏心角。

模型二:刀具的回转中心与刀具的几何中心在一平面内成一定的夹角

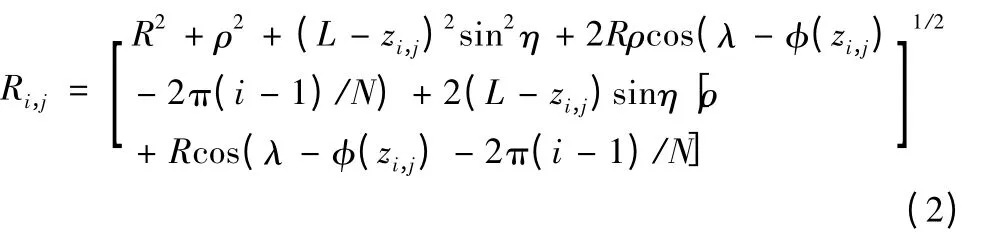
式中，L为安装后的刀具长度，η 为铣刀倾斜的角度。

模型三:刀具的回转中心与刀具的几何中心成一定的空间夹角

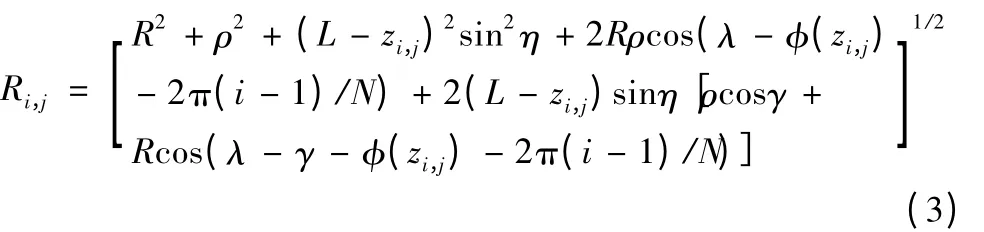
式中，γ 倾斜方向与平面的夹角。

2 刀具偏心跳动对切削厚度的影响分析

由于偏心跳动使得刀齿的实际切削半径和理想切削半径不同，从而导致刀齿切削路径的变化，影响了瞬时未变形切削厚度。因此，在瞬时未变形切削厚度的计算中考虑偏心跳动非常必要。本文采用安装与加工过程中最常见的模型I 对刀具偏心跳动进行分析。根据对刀具切削微元受力情况分析得出未考虑刀具偏心的瞬时切削厚度可近似表示为:

下面加入偏心跳动影响，由于加入后的预测铣削力中参数的个数发生了变化，各个参数的辨识变得相对复杂。为简化辨识过程，考虑适当减少参数的个数。实际应用中λ 一般为μm 数量级，远小于刀具半径，刀具偏心跳动模型I 具有足够的精度，且参数个数相对较少，极大地降低了辨识的难度。结合公式(3)，最终得出考虑了刀具偏心的瞬时未变形切削厚度:

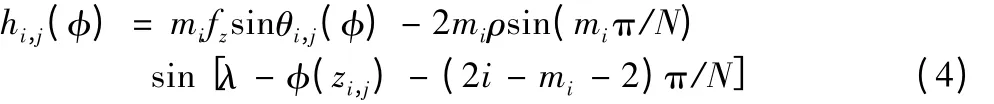
其中:mi为当前切削微元(i，j)瞬时切除的材料是前几个刀齿应该切除的，fz为每齿进给量。

图1 偏心跳动对瞬时未变形切削厚度的影响

3 刀具偏心引起的铣削力计算

实践表明，当切削力系数为常数时，预测到的铣削力的精度并不准确，尤其是小波动时的铣削力难以被预测，为了能够精确反映切削力系数的尺寸效应，提高预测精度，本文采用切削厚度的指数函数和集中表示模型来表示切削力系数，通过分析切削微元，建立某一时刻作用于铣刀上的三个方向的瞬时铣削力为:

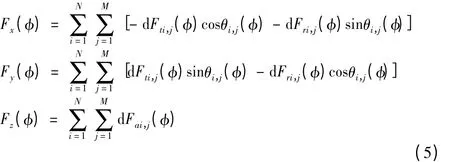
根据铣削实际情况，我们将实测瞬时铣削力分为名义铣削力与由刀具偏心引起的铣削力两个部分，实测铣削力中包含了刀具偏心跳动的影响，但是刀具偏心跳动的参数未知，根据江苏大学王保升博士的《瞬时铣削力模型参数辨识及其试验研究》得知，刀具偏心跳动对名义铣削力没有影响［4］，经过铣削力分解得出由偏心跳动引起的铣削力可以表示为:

4 刀具偏心跳动参数辨识

在上文中，我们建立了三种刀具偏心跳动模型，模型的选择直接影响着参数辨识的复杂程度和精确度，因此我们选择只包含ρ、λ 的刀具偏心跳动模型进行参数辨识。在假设mi =1 的情况下，意味着当前刀齿切除的材料为前一刀齿应该切除却未切除掉的。瞬时切削厚度可简化为:

在已知切削力系数的基础上，通过求取实测值与预测值之差的平方和的最小值来建立刀具偏心跳动系数模型，具体步骤如下:

(1)在铣刀旋转一周内选取S个可以代表波形变化规律的旋转角度作为样本点，获得相应的x、y和z方向上的实测铣削力。即

(2)设置初始值ρ=0，λ=0 。也就意味着此时不存在刀具偏心跳动，因此根据瞬时未变形切削厚度近似表达式hi，j(φ)= fzsinθi，j(φ)计算出瞬时未变形切削厚度，利用瞬时铣削力模型计算出x、y和z方向上的铣削力以及在各个位置角上实测铣削力与预测铣削力差的平方和δ(ρ，λ);

(3)设置迭代步长为Δρ 和Δλ，并使ρ=ρ+Δρ。此时，存在刀具偏心跳动，利用式(4)和铣削力分解式分别计算出瞬时未变形切削厚度和x、y和z方向上的铣削力，同样计算出各个位置角上实测铣削力与预测铣削力差的平方和，δmin=δ(ρ，λ);

(4)设置最大值为ρc，判断ρ ≤ρc是否成立。若成立，计算出判 断δ(ρ，λ)≤δmin是否成立，若成立，赋值ρb =ρ，λb =λ 后重复执行步骤(3)，若不成立，直接重复执行步骤(3)并判断λ ≤2π 是否成立，若成立，则置λ=λ+Δλ 、ρ=0 ，并继续执行步骤(3)，若不成立，则此时的ρ、λ 即为优化结果。利用此方法的流程图如图2 所示［5］。

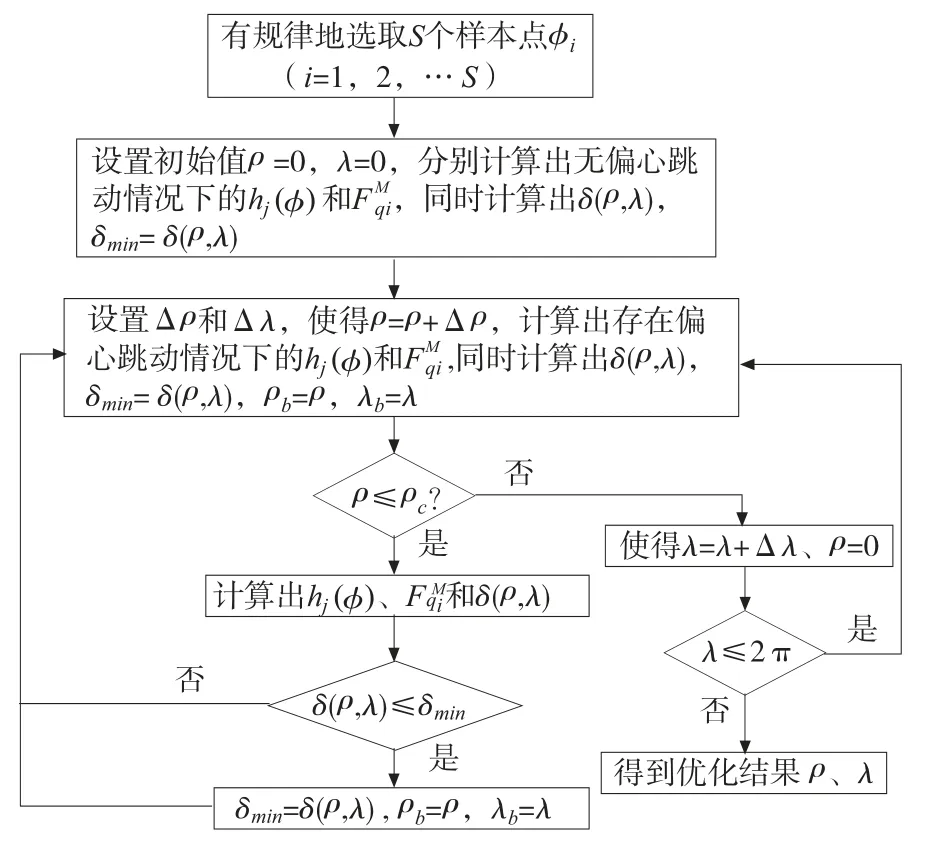
图2 刀具偏心跳动参数辨识流程图

5 刀具偏心参数辨识试验研究

确定参数辨识的原理与过程后，下面通过铣削试验，根据一定的铣削条件进行实际铣削中刀具偏心跳动参数ρ、λ 的确定。在试验过程中，刀具参数不变，保持加工过程处于稳定状态，在合理选择铣削参数—铣削速度、每齿进给量、轴向切深和径向切深的基础上进行试验。试验中选用工件材料为Al6061 -T6，尺寸为90mm×90mm×35mm。选用刀具为平底立铣刀，材料为硬质合金，直径16mm，刀齿数为2，螺旋角为30°。选用机床为德西数控铣床XK—L650，转速范围为60～6000r/min，最大功率为5.5kW，最大转矩为8N.m。铣削方式铣削方式为顺铣，干切削。其他设备及系统测力系统由动态切削测力仪、电荷放大器、数据采集系统及分析软件组成。x、y和z方向上的铣削力通过测力仪转换为电信号，并通过电荷放大器后进行放大，最后输送到数据采集系统由计算机分析软件进行分析处理［6-7］。

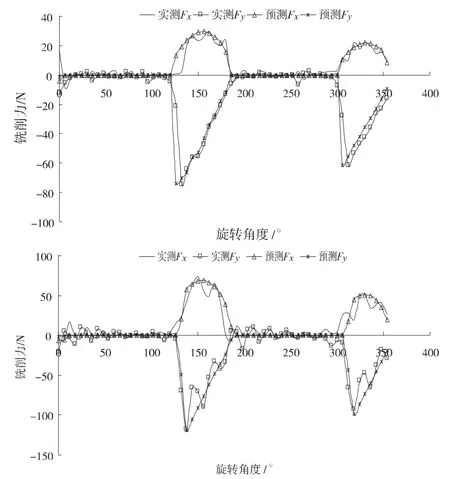
图3 试验1 与试验2 实测铣削力与预测铣削力比较(包含偏心跳动)

依据上述辨识方法，设定初始条件ρ=0 、λ=0 ，偏心跳动参数的最大值为ρc =20μm，搜索步长Δρ=0.1μm、Δλ=1°。以2 组实验的实测铣削数据为基础(具体铣削实验参数见表1)，编写MATLAB 程序，包含偏心跳动因素的实测铣削力与预测铣削力比较图如图3 所示，辨识结果如表2 所示。

表1 铣削参数设计

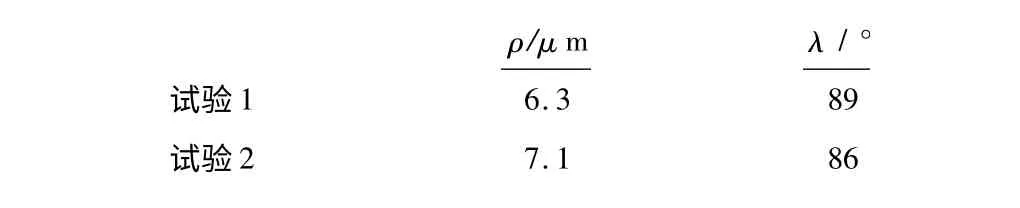
表2 偏心跳动参数辨识结果

由图3 可知，加入刀具偏心跳动参数后，预测出的铣削力与实测铣削力具有相对较好的一致性。而从表2 和大量的试验可以得出，在铣削参数不同的情况下，偏心跳动参数略有不同，刀具偏心量随着进给量与轴深的增加而增加，最后趋于稳定。最终证明了这种偏心参数确定方法的可行性。

6 总结

本文以高速铣削中的铣削参数为研究对象，以平底立铣刀的立铣加工为例对高速铣削中偏心跳动对加工产生的影响尤其是瞬时切削厚度的影响进行分析，建立偏心跳动数学模型，给出了偏心跳动参数偏心量与偏心角度的推理与辨识方法，并通过实验证实了方法的可行性，为高速铣削动态切削力的模型建立以及参数确定提供了帮助。

［1］汪木兰. 数控原理与系统［M］. 北京:机械工业出版社，2008.

［2］王启东，刘战强，汤爱民，等. 平头螺旋刃立铣刀切削力预报模型的建立与数值仿真(一)—刀具几何参数对铣削力的影响［J］. 刀具技术，2011，45(3):17 -22.

［3］王保升. 瞬时铣削力模型参数辨识及其试验研究［D］.镇江:江苏大学，2011.

［4］吴玲，王保升，汪木兰，等.基于遗传算法的铣削参数优化［J］. 组合机床与自动化加工技术，2014(4):108 -111.

［5］潘永智，艾兴，唐志涛，等.基于切削力预测模型的刀具几何参数和切削参数优化［J］. 中国机械工程，2008，19(4):428 -431.

［6］时政博，黄筱调，丁文政，等. 基于自适应控制技术的铣削参数优化［J］.组合机床与自动化加工技术，2012(4):105 -107.

［7］J. M，Zuo，L. Wu，M. L Wang，et al. Efficient prediction of runout parameters in end milling operation［J］.Advanced Materials Research，2013，681 :186 -190.