刀具切削刃钝圆半径的图像测量法*

曾志伟，蒋代君

(西华大学 机械工程与自动化学院，成都 610039)

0 引言

机械加工中，刀具切削刃钝圆半径对切削力、应力分布、刀具磨损、能耗以及成品表面粗糙度等有重要影响［1-4］。切削刃钝圆半径的精确测量成为影响加工质量和效率的重要因素。三坐标测量仪是一种传统的测量工具，具有价格昂贵、操作复杂的弊端。随着计算机技术的发展，数字图像处理在刀具测量领域已得到越来越多的应用。其中的边缘检测和刃口曲线计算对系统测量精度最为重要。

一些经典算子可用于边缘检测，如Roberts、Sobel、Prewitt、Laplacian、LoG 和Canny 算 子 等［5-6］。Roberts算子边缘定位较准确，但不具备噪声抑制力。Sobel 和Prewitt 算子边缘定位较准确且有一定的噪声抑制力，但容易检测到多像素边缘。Laplacian 算子能准确定位阶跃型边缘，但容易检测到不连续边缘，噪声抑制力差。LoG 和Canny 算子具有较强的噪声抑制力，但同时也将尖锐边缘平滑掉。实际的图像总含有噪声且灰度递变地并不剧烈，上述算子难以得到连续单像素边缘，更不能实现边缘的亚像素级定位，所以不适用于刀具的精确测量。为此，Lim 等［7］提出在包含边缘的感兴趣区域(Region of Interest，ROI)，沿近似的梯度方向提取像素，拟合灰度曲线，在灰度函数一阶导数曲线上准确定位边缘点的方法，有效提高了切削刃钝圆半径测量精度。但该方法没有充分利用边缘附近灰度等值线分布规律，对梯度方向的近似计算还不够准确。对于刃口曲线计算，如今多数方法都是直接采用检测到的圆弧部分边缘点拟合刃口曲线。这些方法没有考虑到刀具直线段和圆弧段刃口曲线相切的几何关系［8-9］，圆弧段刃口曲线拟合精度不高，切削刃钝圆半径测量误差较大。文中将给出改进的边缘检测和含约束条件的刃口曲线计算方法，并在实际测量中验证边缘检测的准确性和切削刃钝圆半径的测量精度。

1 材料和方法

1.1 实验

实验选用办公扫描仪采集刀具图像。它在运行时提供较为理想的光照条件，采集的图像质量稳定，最大输出分辨率为12800dip。刀具选用三角形铣刀片，其钝圆半径为0.4mm。图1a 是采集的刀具图像，图1b是其中一个刀尖。

图1 扫描仪采集的刀具图像

为了获取测量系统采集的图像中一个像素的实际尺寸，需要对扫描仪进行标定。标定精度对测量精度有直接影响。实验采用标准量块标定扫描仪，其制造精度在0.0005mm 以下。经计算，系统标定系数为1.9554 ×10-3mm/pixel。

实验中刀具切削刃钝圆半径测量方法见图2，其实现工具为Visual Studio 2010。

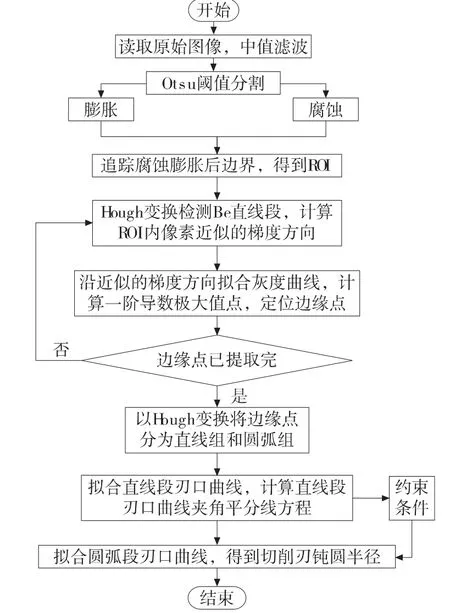
图2 刀具切削刃钝圆半径测量方法

1.2 定义ROI

由于不均匀光照和刀具表面存在的污垢会使采集的图像变得模糊，所以首先对刀尖原始图像进行中值滤波。中值滤波不仅能去除图像噪声，也能较好地保持边缘特性［10］。

边缘是背景和刀具区域的分水岭，边缘附近梯度大于背景和刀具区域梯度(见图3b)，将边缘附近梯度较大的区域定义为ROI。显然，ROI 以外的梯度信息与边缘检测无直接关系，ROI 内梯度信息能完整反映边缘附近灰度递变情况，所以将边缘检测的范围限制在ROI 内。这不仅能节省计算时间，而且由于ROI 边界大致平行于刀具边缘，这在边缘检测时会很有用。为得到ROI，首先从背景中分离出刀具。因为扫描仪内置LED 光源提供了较好的光照条件，刀具背景灰度变化较小，采用Otsu 阈值分割效果较好。对阈值分割图像(见图3a)分别进行形态学腐蚀和膨胀，刀具边界收缩、扩张形成新的边界Be、Bd。用链码技术跟踪Be、B［11］d，则二者之间的区域就是ROI (见图3b)。

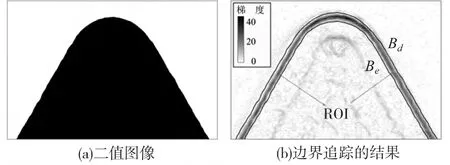
图3 包含刀具边缘的ROI

1.3 计算边缘检测方向

设g(x，y)为灰度函数。如图4a 所示，在Be上取点O，作垂线OP。由于ROI 内灰度等值线大致平行于Be，OP大致垂直于OP方向的灰度等值线，所以OP方向可近似作为该方向上各像素(如P1、P2、P3)的梯度方向，从O点开始、g(x，y)沿OP方向的灰度变化率最快。同理，可将Be上其他像素的法线方向近似作为该法线方向上各像素的梯度方向。刀具边缘附近灰度在梯度方向递变地最剧烈。

图4 计算ROI 内像素近似梯度方向

为计算边缘检测方向、即梯度方向，Lim 等采取的方法是，将刀具图像分割成几部分，此时各部分中Be、Bd上像素数量相差不大，然后将各部分的Be、Bd上像素按顺序配对，并把配对像素的连线方向近似作为该方向上各像素的梯度方向。该方法有两点不足:①Be、Bd上配对像素的连线方向不一定垂直于ROI 边界，也就不一定垂直于灰度等值线，所以对梯度方向近似的准确度不够高;②ROI 直线段内各像素的梯度方向都可以近似成同一方向、即该段ROI 边界Be的法线方向，Lim 等的方法会造成重复计算。

本文以Be上像素的法线方向近似该法线方向上各像素的梯度方向。如图4b 所示，采用改进的Hough变换［12］，检测Be左、右部分直线la、lb，计算la、lb夹角平分线lm，lm与Be交于点G。在角平分线上找到点H，使H到la的距离等于GH。过H作la、lb的垂线，两条垂线分别与Be交于D、F，此时ROI 由D、F分成三部分。ROI 直线部分某像素的梯度方向就是la或lb的法线方向，圆弧部分某像素梯度方向为此像素与H的连线方向。显然，ROI 直线段内各像素的梯度方向只需计算一次，且由于ROI 边界大致平行于灰度等值线，所以对梯度方向近似的准确度也比较高。

1.4 检测边缘

为检测刀具边缘，设灰度函数:

则

式中:f(a0，…，a5)—目标函数;

Gi—第i个像素的灰度;

Ri—第i个像素与起始像素间的距离。

式(1)的最优解就是g(r)的参数。如图5a 所示，在Be上取点Q并沿其e1方向提取像素，由(1)式拟合灰度曲线并计算灰度变化率曲线，结果见图6 中曲线1 和曲线2。那么，所得到的e1方向灰度变化率极大值点E1(见图5b 和图6 的点5)是不是边缘点呢?如果E1是边缘点，则E1也必定是过E1垂直于刀具边缘方向(e2方向)上的灰度变化率极大值点。为此，过E1作Be垂线，沿垂足V的e2方向提取像素(见图5a)，拟合灰度曲线并计算灰度变化率曲线，结果见图6 中曲线3 和曲线4。计算表明，e2方向灰度变化率极大值点是E2(见图5b和图6 的点6)，所以E2才是准确的边缘点。虽然此例中E1仅偏离边缘点E2约0. 6 个像素，但若提取像素的方向更为偏离梯度方向，边缘点的计算误差会更大。所以，沿梯度方向才能检测到准确的边缘点。

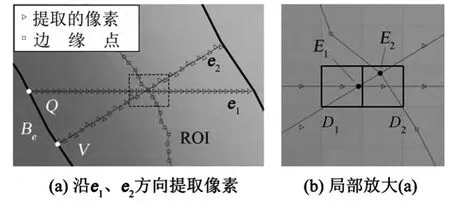
图5 沿e1、e2 方向检测边缘

图6 e1、e2 方向的灰度曲线及灰度变化率曲线

1.5 计算刃口曲线

在计算刀具刃口曲线前，采用Be的分段方法，将边缘点分成直线组和圆弧组。

在刀具的设计和加工中，为方便制造、测量和检验，常用圆弧和直线的组合代替刃口曲线，此时要保证直线与圆弧之间光滑连接。但通常的刀具刃口曲线计算方法并未将此考虑在内，都是直接利用圆弧组边缘点拟合刃口曲线方程。这些方法的不足，一是圆弧组边缘点较少，拟合的刃口曲线精度不高;二是没有充分利用直线组边缘点。所以，在拟合圆弧段刃口曲线时，提出如下约束条件:

(1)刀具圆弧段刃口曲线圆心处于两条直线段刃口曲线形成的刀尖角的角平分线上。

(2)刀具圆弧段刃口曲线半径等于圆心到两条直线段刃口曲线的距离。

设刀具直线段刃口曲线l1、l2的方程为:

则

式中:f(k1，b1)—l1的目标函数;

f(k2，b2)—l2的目标函数;

(Xi，Yi)—l1第i个边缘点坐标;

(Xj，Yj)—l2第j个边缘点坐标。

式(4)的最优解就是l1、l2的参数。设l1、l2相夹的刀尖角的角平分线l3的方程为:

l3的参数由l1、l2的方程联立解出。设刀具圆弧段刃口曲线c的方程为:

则

式中:f(a，b，r)—c的目标函数;

(Xi，Yi)—c的第i个边缘点坐标;

h1(a，b)—约束条件(1)对应的函数;

h2(a，b，r)—约束条件(2)对应的函数。

式(7)的最优解就是c的参数，由此可得刀具切削刃钝圆半径。

2 结果和讨论

测量刀具切削刃钝圆半径时，先将(7)式中的约束条件去掉、直接用圆弧组边缘点拟合刃口曲线，再以本文提出的约束条件拟合刃口曲线，相关结果见表1。无约束图像测量误差为7%，测得的切削刃钝圆半径普遍偏小，故系统误差较大，测量准确度较低。有约束图像测量误差为0.5%，测得的切削刃钝圆半径比较集中和均匀地分布在0.4mm 附近，故系统误差和随机误差均小，测量的准确度较高。

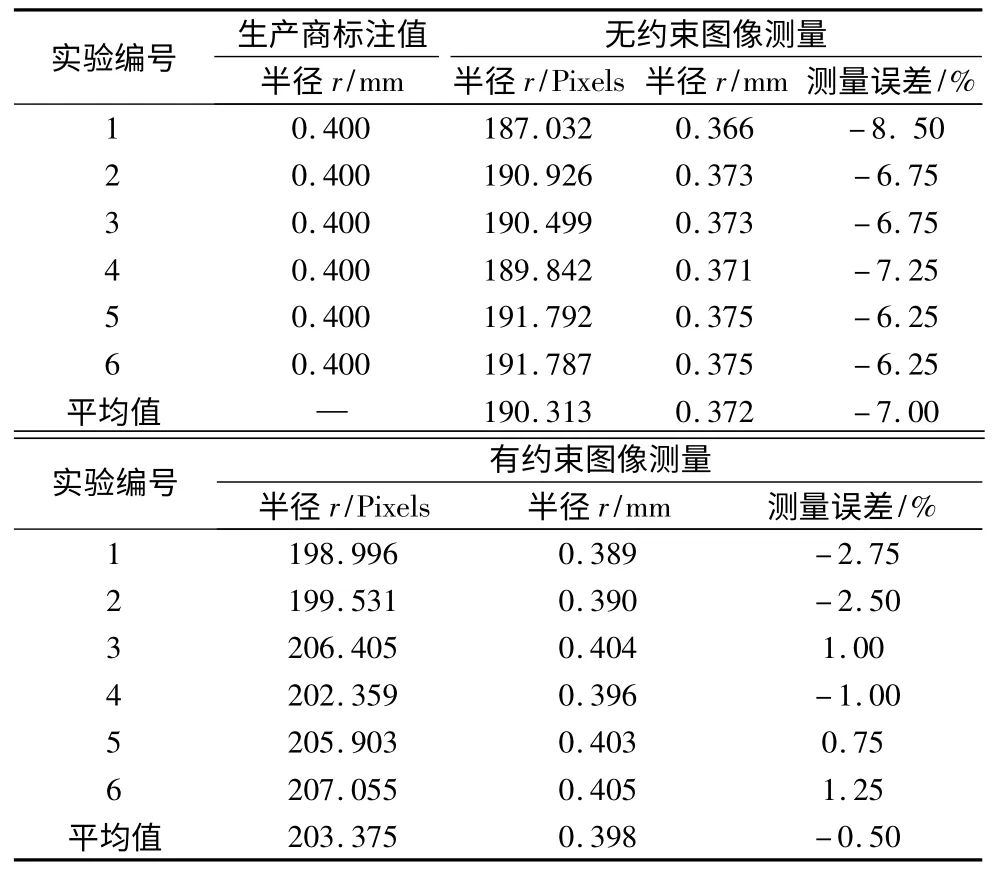
表1 刀具切削刃钝圆半径的测量结果

无约束图像测量误差偏大的原因是，圆弧组边缘点仅占完整圆周的小部分，较大的数据噪声会影响圆心的定位和半径的计算精度［13-14］。设c的圆心到l1与l2的距离分别为d1、d2。理论上，d1=d2=r= 0.4mm。如图7 所示，实验中的d1、d2大于r，说明c和l1、l2无交点。d1与d2差值显著，说明c的圆心明显偏离角平分线l3。d1、d2小于0.4mm，说明c的圆心离l1、l2过近，所以切削刃钝圆半径测量值偏小。可见，用较少的数据无约束拟合c，c圆心的定位和半径的计算精度并不高。利用刀具直线段和圆弧段刃口曲线相切的几何关系，对圆心和半径进行约束，可显著提高圆心的定位和半径的计算精度。这种方法在测量新刀具时效果较好。

3 结论

(1)刀具ROI 边界像素法线方向可以比较准确地近似该法线方向上各像素的梯度方向。沿近似梯度方向提取像素，可以拟合一条变化率最快的灰度曲线，从而可在相应的灰度变化率曲线上精确定位边缘点。

(2)以刀具直线段和圆弧段刃口曲线相切作为约束条件，最优化拟合圆弧段刃口曲线，使切削刃钝圆半径的测量误差从不加约束的7%减小到加入约束的0.5%。改进的刃口曲线计算方法可以显著提高切削刃钝圆半径的测量精度。

［1］Nath C，Rahman M，Neo K S. A study on the effect of tool nose radius in ultrasonic elliptical vibration cutting of tungsten carbide［J］. Journal of Materials Processing Technology，2009，209(17):5830 -5836.

［2］Liu M，Takagi J，Tsukuda A. Effect of tool nose radius and tool wear on residual stress distribution in hard turning of bearing steel［J］. Journal of Materials Processing Technology，2004，150:234 -241.

［3］Chou Y K，Song H. Tool nose radius effects on finish hard turning［J］. Journal of Materials Processing Technology，2004，148(2):259 -268.

［4］吴红兵，刘刚，毕运波，等. 刀具几何参数对钛合金Ti6Al4V 切削加工的影响［J］. 中国机械工程，2008，19(20):2419 -2422.

［5］邹福辉，李忠科. 图像边缘检测算法的对比分析［J］. 计算机应用，2008，28(6):215 -216，219.

［6］段瑞玲，李庆祥，李玉和. 图像边缘检测方法研究综述［J］. 光学技术，2005，31(3):415 -419.

［7］Lim T Y，Ratnam M M. Edge detection and measurement of nose radii of cutting tool inserts from scanned 2-D images［J］. Optics and Lasers in Engineering，2012，50:1628 -1642.

［8］刘杰华. 刀具精确设计理论与实践［M］. 北京:国防工业出版社，2005.

［9］宋寅，姚彬，沈志煌，等. 可转位刀片圆弧过渡刃曲面的成形理论［J］. 机械设计，2013，30(6):90 -93.

［10］赵高长，张磊，武风波. 改进的中值滤波算法在图像去噪中的应用［J］. 应用光学，2011，32(4):678 -682.

［11］史进伟，郭朝勇，刘红宁，等. 一种快速提取弹底底火表面缺陷图像方法［J］. 计算机工程与应用，2013，49(17):154 -158.

［12］张红霞. 基于机器视觉的旱田多目标直线检测方法的研究［D］. 北京:中国农业大学，2007.

［13］朱嘉，李醒飞，谭文斌，等. 基于圆心约束最小二乘圆拟合的短圆弧测量［J］. 光学精密工程，2009，17(10):2486 -2492.

［14］刘珂，周富强，张广军. 半径约束最小二乘圆拟合方法及其误差分析［J］. 光电子·激光，2006，17(5):604 -607.