基于调度序列的大型公共设备规划优化设计研究*
2014-06-29杨建国
张 昕,施 烁,杨建国
(1.上海电气机床成套工程有限公司,上海 200041;2.东华大学 机械工程学院,上海 200051)
0 引言
车间生产调度问题是最困难的约束组合优化问题[1],因为没有有效的算法能在多项式时间之内算得它的最优解。对于许多具有大型工件的加工车间而言,车间的调度问题除了一般的工件与机床的约束关系之外,还要受到例如行车、自动化小车(AGV)等公共资源的约束。由于通常行车数量受限,故大型工件的搬运除了考虑工序完工时间之外,还要考虑大型工件搬运路径、搬运时间等约束[2]。
在实际生产过程中,大型公共设备的运输时间涉及行车的行走路径,即设备布局情况。在本文算法中,先用遗传算法解决基本车间的调度问题,得出调度最优解后,在调度序列的基础上,进行公共设备规划设计。在公共设备规划设计时,考虑其现有车间布局,动态搜索大型公共设备行走路径,利用动态右重移策略解决大型公共设备合理规划问题。
1 调度问题
大型公共设备调度问题可以描述为:n个工件{J1,J2,…,Jn},在m台设备{M1,M2,…,Mm}上加工。每个工件由一系列工序Ojx(x=1,2,…,TOj)组成,Ojx和TOj分别表示工件j的第x道工序和工件j的总工序数;工序Ojx在指定设备Mijx上加工,Mijx∈(M1,M2,…,Mm),加工时间为tijx;其中n个工件中有q个工件是重型工件,对于某一个重型工件,其加工工序Ojx及Oj(x+1)之间必须有一个大型公共设备的运输时长Njx,(x+1),且大型公共设备使用次数为TOj。大型公共设备的运输优先级与加工时间的先后顺序有关,且运输时长与大型公共设备的行走路径有关。同时,加工过程中,根据调度模型,作出如下假设:
①每一个设备位置点旁有货架缓冲区;
②设备旁货架缓冲区可存放的工件数不限;
③每个货架缓冲区与设备加工区属于同一区域,该区域内不再使用大型公共设备;
④大型公共设备的起始位置默认为初始工序的搬运位置;
⑤同一重型工件的工序之间使用大型公共设备具有不同的优先级;
⑥不同重型工件的工序之间使用大型公共设备具有不同的优先级;
⑦同一时刻大型公共大型设备只能运输一个工件。
在满足上述条件的前提下对大型公共设备调度模型中的工件进行调度安排,确定每个工件的加工设备以及在各台设备上的开工时间,考虑大型公共设备生产调度过程中涉及的目标函数[3-4]:工件完工时间,建立(1)所示目标,使工件最大完工时间最小。
min(f1)=min(makespan)=min(max(Ci)) (1)其中,设Ci表示第i个工件的完工时间。
2 调度问题模型构建
2.1 车间布局的数学描述
车间设施布局就是按照一定的原则,在已确定的车间场地内,合理地安排车间内部各类加工设施、辅助服务设施等的具体位置,并对人员及物料的移动路线做最可行的设计。既保证生产活动能有效进行和获得最大的生产经济效益,又为员工提供一个安全、方便、舒适的工作环境[5]。
现已知,普遍应用的典型布局方式有:按工艺布置、按产品布置、按固定工位布置和按成组生产原则布置。根据调研可知,某车间为按工艺布置方式。按车间布局即是将相近的工艺归入同一组,如车床组、五轴加工中心组、三轴立式加工中心组、铣床组等,并基于设施间的物流来确定一个工艺设备相对另一个设备的位置,在制造业内广泛用于单件小批量生产方式。按工艺布置见图1。
车间布局矩阵与车间布局及大型公共设备的轨道方向有关。其中车间多为矩形c·d,大型公共设备的轨道方向与车间矩形一致。车间布局矩阵大小为p×q,其中p代表该车间d 方向最大设备行数,q代表该车间c 方向最大设备数,当矩阵对应的位置处无设备则用0 表示。由图1 知,则p=4,q=5。则车间布局矩阵为:
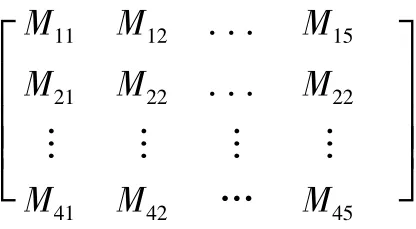
其中M11对应图1 中车床1。
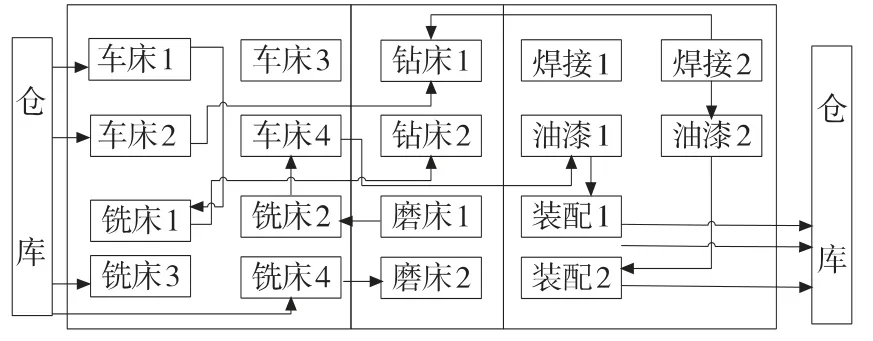
图1 按工艺布置车间布局图
2.2 工件信息的数学描述
若已知有n个工件{J1,J2,…,Jn}参与调度,其中有q个重型工件{q=1,2,3...n-1},则工件矩阵大小为的矩阵,其中重型工件在矩阵中用1 表示,普通工件用0 表示。假设参与调度的工件共有J1,J2,J3,则矩阵表示为[0 1 0 ],其中J2为重型工件。
2.3 大型公共设备动态路径规划
(1)大型公共设备行走路径计算公式
在启用大型公共设备运输重型工件时,考虑大型公共设备运行平稳为匀速运动,忽略其设备初始时间,即起吊时间。可知,大型公共设备运输时其位置由初始设备转至另一设备的时间与其行走路径和车间布局有关,且和车间布局中设备间的距离有关[6]。
根据2.1 节车间布局的数学描述及车间布局矩阵,计算大型公共设备行走路径。其计算公式见式(2)、(3)、(4)。
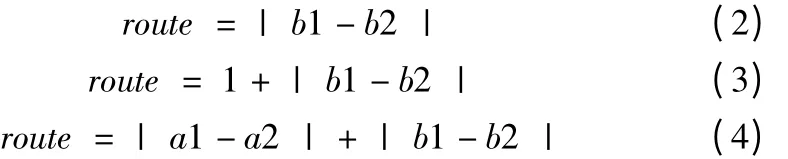
式中,(a1,b1),(a2,b2)代表设备M1、M2在车间布局矩阵中的位置坐标。式(2)表示车间方向c 上,大型公共设备在车间布局矩阵中同一行设备中转移的路径计算公式。式(3)表示车间方向c 上,大型公共设备在车间布局矩阵中相邻两行设备间转移的路径计算公式。式(4)表示在车间方向c 上,大型公共设备在车间布局矩阵中非相邻非同行两行设备间转移的路径计算公式。
(2)大型公共设备行走时长计算
大型公共设备行走时长的计算与行走路径,车间中设备间的距离dis及大型公共设备行走速度v相关。由于默认大型公共设备起始位置默认为初始工序的搬运位置,故大型公共设备第一步行走时长为0。行走时长T=(dis×route)/v。
(3)工序优先级确定
一般地说,大型公共设备路径行走的关键问题在于解决多个重型工件之间工序的优先级问题。已知同一工件工序间的加工具有优先级顺序,而不同工件工序间的加工具有相同优先级[7-8]。采用遗传算法求解出调度最优结果,根据最优结果中各工序的起始加工时间,可得出多个重型工件的工序加工优先级矩阵。根据多个重型工件的加工优先级矩阵,可得出大型公共设备的初始行走路径。
(4)右重移策略
右重移策略常用于解决动态调度问题[9],当紧急工件插入时,未受影响的工序统一向右移,右移量为紧急工序的时长。算法中将大型公共设备运输时间作为紧急插入时间来处理,但与紧急工件工序插入的解决策略并不完全一致。图2 为示例甘特图,虚线矩形为重型工件工序。根据大型公共设备的调度模型之可知,默认大型公共设备的初始位置在第一道工序处,故其搬运路径为0,下一步搬运是从初始位置1/1(工件1 工序1)处至如图中在虚线部位1/2(工件1 工序2)处,插入大型公共设备的运输时长,此步的右重移策略过程如下:
步骤1:由大型公共设备行走路径公式计算大型公共设备从初始位置1/1 处运输至1/2 处的行车行走路径,以及行走路径时长即M3至M2的运输时间t,大型公共设备运输将重型工件从原始位置运输至下一加工位置的设备,即图2 中设备为M2。
步骤2:大型公共设备运输至M2上时,该重型工件工序(工件1 工序2)以及在M2设备上在重型工件工序之后加工的所有工序,向右移t的时间量。
步骤3:其他设备(不包括大型公共设备运输至的设备,如图2 中M1,M3)上工序时间右移判断。其他设备,若插入时间点(工件1 工序2 的加工起始时间)在该工序加工过程中(如工件3 工序1),则该工序之后的所有加工工序(如图2 中工件1 工序3),向右移t的时间量;否则,该插入时间点后的所有加工工序向右移t的时间量(如图2 中工件3 工序2 和工件2 工序3)。
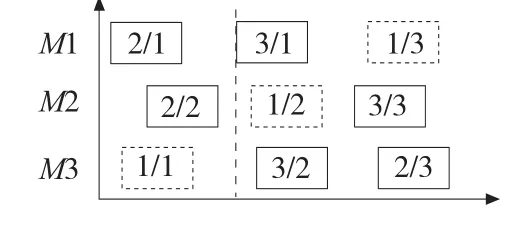
图2 右重移策略图
3 混合遗传算法的实现
步骤1:读取调度任务信息及车间布局矩阵信息;
步骤2:将所得任务信息处理成遗传算法所需的设备约束矩阵、时间约束矩阵,工件信息矩阵及车间布局矩阵,同时初始化大型公共设备路径矩阵和工序优先级矩阵。
步骤3:将设备约束矩阵及时间约束矩阵作为遗传算法的输入并输入。
步骤4:采用遗传算法求解调度问题。输出其调度起始时间矩阵以及调度终止时间矩阵。
步骤5:根据步骤4 中的调度起始时间矩阵、调度终止时间矩阵和步骤2 中的工件信息矩阵及车间布局矩阵,生成公共设备路径矩阵Route。
步骤6:设置计数器i=0;
步骤7:读取路径矩阵Route(i)中的设备,并计算出该路径范围内路径行走时长。
步骤8:判断行走路径是否需要添加多工件同时运输工序,若是则确定多工件同时运输工序并计算器行走时长,否则转入步骤9。
步骤9:采用动态右重移策略,将该路径的行走时长插入至调度结果中。
步骤10:更新调度起始时间矩阵、调度终止时间矩阵。并根据更新后的起始时间矩阵和终止时间矩阵得出更新后的路径矩阵及工序优先级矩阵。
步骤11:i=i+1,若i=N,则输出调度结果,算法终止。否则,返回步骤7。
步骤12:结束,见图3。
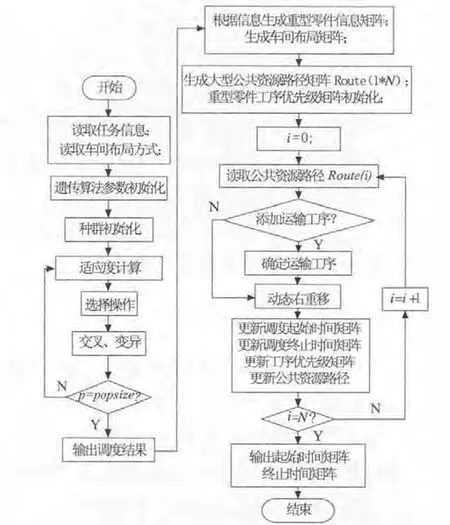
图3 公共设备调度流程图
4 应用示例
根据大型公共设备优化方法,利用该方法针对大型公共设备优化调度实例进行测试,以验证方法的有效性。测试案例来源于案例ft06(6* 6)案例[10],见表1。同时根据车间实际生产情况,确定车间的约束见表2。调度最优解的遗传算法参数为:种群大小popSize=50,迭代次数maxGen=40,选择算子psel=0.1,交叉因子pxover=0.85,变异因子pmutation=0.2,保优个体数=3。
调度结果见甘特图,如图4 所示。由测试得ft06案例调度最优解makespan=55,已知现有ft06 案例的最优解为55。在ft06 案例最优解的基础上,考虑大型公共设备优化的调度结果为MakeSpan=64。大型公共设备优化方法可得,大型公共设备的行走路径为:M2→M4→M6→M1→M5→M3;对应大型公共设备行走时长为:0→2→2→3→2→2。图中,矩形作为边界表示大型公共设备的优化情况。

表1 ft06 设备/时间约束
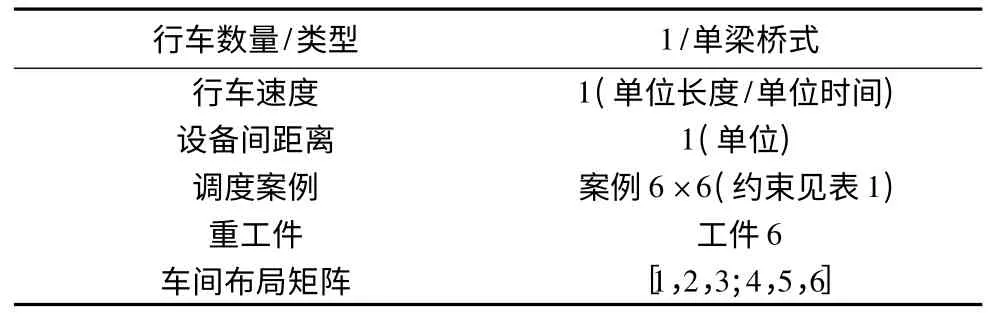
表2 车间约束
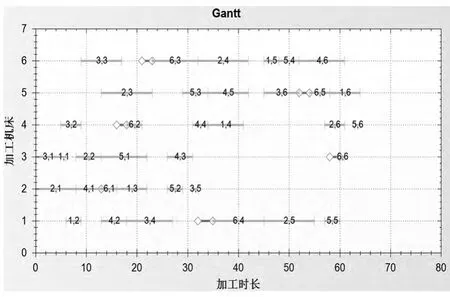
图4 大型公共设备调度甘特图
5 结束语
本文建立了大型公共设备调度模型,对算法关键部分进行了详细设计。在调度序列的基础上,构造了车间布局、工件信息、大型公共设备行走路径和行走时长的数学计算模型,同时制定了动态右重移策略,实现大型公共设备优化规划的目的。
[1]BRUCKER P,SCHLIE R. Job-Shop scheduling with multi-purpose machines[J]. Computing,1990,45(4):369-375.
[2]BRANDIMARTE P. Routing and scheduling in a flexible Job-shop by taboo search[J]. Annals of Operations Research,1993,22(2):157 -183.
[3]王海瑶,蒋增强,葛茂根.基于规则组合的Job Shop 多目标柔性调度方法[J].合肥工业大学学报(自然科学版),2010,33(1):14 -18.
[4]余建军,孙树栋,刘易勇.基于免疫算法的多目标柔性Job Shop 调度研究[J].系统工程学,2007,22(5):214 -222.
[5]NELSON R,HOLLOWAY C,WONG R. Centralized scheduling and priority implementation heuristics for a dynamic Job Shop model with due dates and variable processing time[J].IIE Transactions,1997,9(1):96 -102.
[6]帅旗,姚锡凡.基于启发性规则及关键路径调整的柔性作业调度优化算法[J].西南交通大学学报,2012,47(3):509-515.
[7]袁 坤,朱剑英.一种求解多目标柔性Job Shop 调度的改进遗传算法[J].中国机械工程,2007,18(2):651 -656.
[8]赵有辉.动态多目标柔性调度问题的改进遗传算法研究[J].电脑知识与技术,2012,8(4):829 -832.
[9]潘全科.智能制造系统多目标车间调度研究[D]. 南京:南京航空航天大学,2003.
[10]MUTH J,THOMPSON G E. Industrial Scheduling[R].Prentice Hall.NJ:Endlewood Cliffs,1963.
