基于元结构分析的三坐标加工单元立柱优化研究
2014-06-29邹志华郑金来喻道远周小强张永杰
邹志华,郑金来,喻道远,周小强,张永杰
(1.华中科技大学 数字制造装备与技术国家重点实验室,武汉 430074;2. 江苏高精机电装备有限公司 技术中心,江苏 盐城 224053)
0 引言
立柱是三坐标加工单元的关键支撑部件,它底部连接机床底座,顶部支撑主轴箱、刀库等关键部件,其动态性能关系到整个机床的工作性能,将直接影响到加工中心的稳定切削及加工精度,因此对其进行详细的动态特性分析显得尤为重要。
机床立柱内部加强筋的结构、布局等在很大程度上决定了机床立柱结构的动态性能,但往往由于立柱结构设计不合理,导致立柱的刚度不足,产生各种变形、振动[1]。合理地选择和布置立柱内部加强筋是提高立柱刚度的一个有效措施。众多学者对床身筋板结构进行了优化研究[2-8]。但是他们并未对在不同外形尺寸下何种加强筋动态特性更好做出明确研究,本文以立柱结构为研究对象,利用ANSYS 软件对立柱进行动态特性计算分析,以立柱的固有频率为优化目标,重点研究不同元结构单元的动态特性,得到不同尺寸大小下的最优元结构类型;最后以优选的元结构单元对立柱加强筋进行重新布置设计,获得了动态性能更好的立柱结构。
1 立柱有限元模型
几何模型是进行有限元分析的基础和前提。本文采用Pro/E 软件建立立柱的三维实体模型,然后将其转换为CAE 模型,再导入ANSYS 进行动态特性计算分析。在建模过程中对结构进行了适当的简化与修改,忽略模型中对分析结果影响较小的特征,如部分倒角、凸台、小孔等[9]。图1 为简化后的立柱三维实体模型,图2 为简化后立柱的有限元网格划分模型。

图1 立柱三维实体模型

图2 立柱有限元网格划分模型
2 立柱结构的有限元模态分析
2.1 模态分析理论
模态分析是用来研究结构振动特性的重要手段,通过模态分析能够确定复杂结构的振动形态和薄弱环节。模态是系统结构的固有特性,与外载荷无关,进行模态分析时,不需要设置外载边界条件;由于阻尼对结构的固有频率和振型影响很小,所以不考虑系统阻尼的影响。对于一个n自由度的无阻尼振动系统微分方程可表示为:
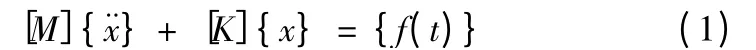
式中:[M]、[K]分别为结构的总质量矩阵和刚度矩阵;{f(t)}为外激励矩阵,这里为零矩阵;{x}、{¨x}分别为物理坐标系下结构的位移向量和加速度向0 量。式(1)的特征值方程为:

求解特征值方程式(2)就可以得到ω 和{x},即系统的固有频率和主振型;解此方程得ω 的m个互异正根,ω0i(i=1,2,3…,m),并按升序排序,

第i阶固有频率:

各阶固有频率f0i均与成正比,f0i大,说明单位质量的刚度高,可作为结构动态设计的一个优化目标。固有频率与主振型是振动系统最基本的固有属性,不会随意改变,只有在被激励时才表现出来。
2.2 立柱结构模态分析
立柱在实际工作中并非处于自由状态,而是和机床连在一起,处于约束状态,根据立柱的实际工作状态,可认为立柱底端发生的位移量很小近似于零,可对立柱的底端施加X、Y、Z三方向的自由度约束。在理论与实践中发现,结构的低阶模态对结构的振动影响较大,只有低阶模态的频率才有可能与激振频率重合或接近,高阶固有频率已远高于可能出现的激振力频率,一般不会发生共振。立柱材料为灰铸铁HT250,弹性模量E= 1. 15GPa,泊松比μ = 0. 265,密度ρ =7100kg/m3。综合分析各种模态提取方法的特点[10],本文采用Block Lancozos 法求解立柱模型的固有频率和振型,得到立柱的前6 阶固有频率列表如下表1 所示,前6 阶振型如图3 所示。
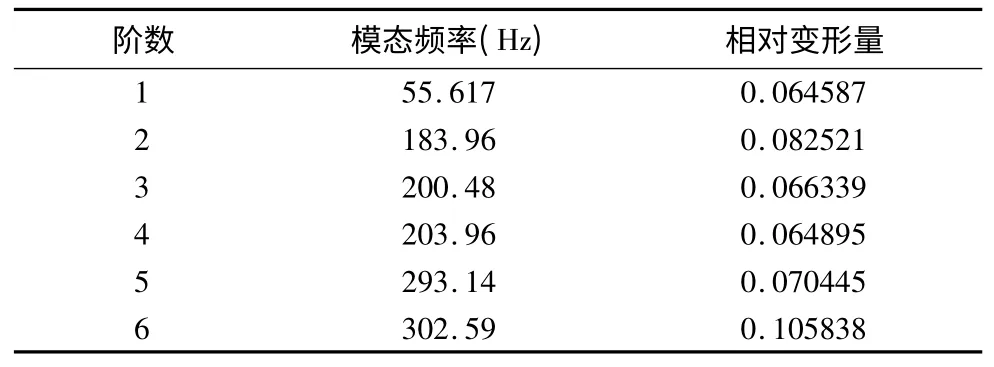
表1 立柱模态频率

图3 立柱的各阶振型图
综合立柱前6 阶的模态频率及振型进行对比分析知:其一阶模态阵型是沿立柱Z轴方向的来回振动,立柱由下到上振动的幅度不断增强,最大振幅发生在立柱的顶部;二阶模态阵型为立柱整体绕Y轴的扭转振动,振幅最大值发生在立柱顶部的四个角上;三阶模态为立柱沿X方向的来回振动;四阶模态为立柱沿Z方向的膨胀挤压振动,对立柱结构有很大的破坏性;五阶、六阶振动频率相差较小,阵型均为向Z方向的弯曲振动。立柱两侧的壁板的扭转振动及弯曲振动比较大,是立柱结构中比较薄弱的环节,同时立柱的振动势必会将影响与之相连的机床底座和主轴箱等部件,影响加工质量,应当引起重视并加以改进。
3 立柱结构的优化分析与改进
3.1 元结构单元动态特性分析
元结构的基本思想是把机械结构大件就其组成形体进行分解,最终得到一些拓扑结构变化不大、相对独立的基本单元结构,其单元结构特性会影响到整个结构特性的优劣。若从动态设计角度优化这些元结构,能得到其变量化的优化尺寸参数;若以固有频率和振型为目标优化这些元结构,能获得元结构的合理的尺寸模型,供快速设计选用。通过立柱模态分析可知,立柱两侧壁板对其动态性能有很大的影响,可以通过改变立柱加强筋的布置方式,来提高其动态特性。
立柱加强筋纵横交错,由口字型结构重复排列构成,即口字型结构为立柱的元结构单元。现以构成立柱加强筋板结构的一个元结构单元为研究对象,将其简化为由板单元围城的六面体结构。常用的4 种立柱加强筋元结构形式如图4 所示。形式1 为加强筋交叉布置的的十字型;形式2 为加强筋交叉布置的X 型;形式3 为加强筋交叉布置的星型;形式4 为加强筋交叉布置的米字型。元结构的尺寸设置如下:长度L=300mm,宽度B=300mm,厚度T1 =20mm,加强筋厚度T2 =50mm,加强筋宽度b1 =15mm,b2 =2b1 =30mm,针图示形式的元结构进行有限元计算分析,元结构单元四周固定(约束条件),计算出各单元的低阶振动频率,下表2 为上述元结构单元的前6 阶固有频率。

图4 各种元结构单元

表2 各种元结构单元的固有频率(单位:HZ)
为了更直观地看出元结构单元对固有频率的影响,下面就把第一阶频率变化曲线图给出,如下图5 所示,横坐标是元结构单元类型,1:空白型,2:十字型,3:X 字型,4:星字型,5:米字型;纵坐标是元结构单元的固有频率(单位:Hz)。
比较图表中的模态分析结果知:在上述尺寸形式下十字型、米字型的前6 阶固有频率较高,动态性能较好,星字型次之,X 字型动态性能最差;X 字型结构看上去较十字型更稳定,但是其动态特性却不一定较好,其一阶固有频率也由3817.1Hz 下降到3096.2Hz;十字型和星字型相比,后者虽然增加了一条加强筋板,表面看是增加了它的刚度和强度,但其固有频率并未随之提高,一阶固有频率由3817.1Hz 下降到3495.1Hz,可见星字型虽然其布局较紧凑,其动态性能未必就理想,这说明盲目地增加加强筋数量,并不一定能提高其固有频率。

图5 一阶固有频率变化曲线
3.2 元结构单元边长比与固有频率的研究
为了使元结构分析应用于复杂结构的设计中,对构造参数化元结构模型进行分析:改变元结构单元中L和B的比值,研究相应的元结构单元的固有频率的变化规律。以L/B的比值为横坐标,元结构单元的一阶固有频率为纵坐标,可绘制如下图6 所示的变化曲线。
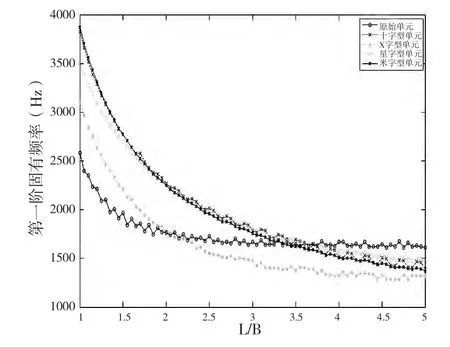
图6 元结构单元一阶固有频率随L/B 值的变化曲线
分析曲线可知,随着L/B的增加,其一阶固有频率呈下降的趋势,并且下降趋势逐渐变缓,单元大的边长比不利于提高其动态特性;总体来看十字型、米字型和星字型有较好的动态特性,X 字型的动态特性较差;当L/B的比值大于2.2 时,X 字型元结构单元的固有频率比没加筋板的原始结构的更低,说明在结构设计中不能盲目的增加加强筋;随着L/B的比值增大,十字型和星字型的动态特性越来越好,在L/B大于1.6后,十字型的元结构动态特性甚至比米字型的动态特性还好,十字型具有较优的动态特性;在L/B大于2.0时,星字型的元结构单元动态性能也比米字型的动态特性好,增加加强筋的数目不一定能提高结构的固有频率;当L/B比值大于3.4 时,原始的空白结构单元动态性能比米字型单元的要好;当L/B值大于3.8 时,原始的空白单元的动态特性甚至超过了星字型,说明增加加强筋不仅不能提高结构的一阶固有频率,反而使结构的动态特性变差,因此在元结构单元边长比L/B的比值要小于3.4 较为合理。
3.3 立柱优化研究
当L/B大于1.6 以后,十字型加强筋的元结构单元为该比例尺寸下的最优元结构类型,并且相比较米字型结构而言质量更轻、更经济;原始的立柱结构中元结构单元L=390mm,B=235mm,其比值L/B为1.66,在不明显改变原有立柱结构基础上,十字型单元为选择的最优单元,以此元结构单元为基础对立柱进行优化设计,下表3 是利用元结构单元优化前后的立柱固有频率(注:A 方案是原始的立柱结构;B 是以X 字型元结构单元优化后的立柱;C 以十字型元结构单元优化后的立柱)。

图7 基于X 字型、十字型单元优化后立柱结构

表3 立柱固有频率(单位:Hz)
经过优化后立柱的一阶固有频率得到了提高,其中X 字型的只提高了3.62%,而十字型的提高了5.45%,与元结构分析的数据吻合,说明通过优化元结构单元来提高立柱的固有频率是可行的。
4 结论
机床立柱采用合理的加强筋结构,既能减轻了立柱的重量,又能保证必要的刚度,有利于提高动态性能。元结构单元的长宽比(L/B)对其固有频率有很大的影响:当L/B的值小于1.6 时,米字型的元结构单元具有最好的动态特性;当L/B的值大于1.6 时,十字型的元结构单元具有较优的动态特性;当L/B的比值增大时,星字型元结构单元的动态特性变好,而X 字型元结构单元的动态特性则较差;星字型结构和十字型结构相比,虽然它较十字型的元结构单元多了一条加强筋,但是其动态特性确并没有变好,盲目设置多根筋板并不一定有利于结构动刚度的提高。总的来说,十字型元结构单元具有较好的动态特性,应该优先进行选择。对比基于元结构单元的立柱结构优化前后的固有频率变化可知,其一阶固有频率提高了5.45%,说明改变筋板的布置形式来提高机床动态性能是可行的。
[1]徐燕申. 机械动态设计[M]. 北京:机械工业出版社,1991.
[2]李小彭,赵志杰,聂慧凡,等.某型数控车床床身的模态分析与结构优化[J]. 东北大学学报(自然科学版),2011,32(7):988 -991 .
[3]陈叶林,丁晓红.机床床身结构优化设计方法[J].机械设计,2010(8):65 -68.
[4]杨明亚,王辉,张长泉. 数控机床床身筋板布局方式的动态性能分析及优化设[J].贵州大学学报(自然科学版),2013,30(1):37 -41.
[5]王富强. 精密机床床身的动态特性分析与优化[D]. 甘肃:兰州理工大学,2007.
[6]Xu Yan-shen ,Zhang Xing-zhao ,Niu Zhan-wen ,etal. Research of dynamic design of machine tools bed structures based on optimization unit structures and frames[J]. Journalof Mechanical Strength ,2001,23(1):1 -4.
[7]张学铃,徐燕申,钟伟泓.基于有限元分析的数控机床床身结构动态优化设计方法研究[J]. 机械强度,2005,27(3):353 - 357.
[8]周自阳,洪荣晶,袁鸿.成形铣齿机床立柱筋板结构优化设计[J].机械设计与制造,2012 (11):149 -151.
[9]胡于进,王璋奇.有限元分析及应用[M].北京:清华大学出版社,2009.
[10]陈新.高精度内圆磨床结构动力学建模与优化设计研究[D].南京:东南大学,2001.
