改进元胞多目标遗传算法在机床主轴优化中的应用*

张 屹，万兴余，郑小东，余竹玛

(三峡大学 水电机械设备设计与维护湖北省重点实验室，湖北 宜昌 443002)

0 引言

机床主轴是机床的核心部件，其作用是带动刀具旋转，直接参与高速切削加工。机床主轴的好坏对机床的加工精度，表面质量和生产率影响很大。国内外不少科研人员对机床主轴进行了一系列科学研究，但大多数都是集中在提高主轴的某一个性能，例如，减少变形，提高刚度或者是减小振动或者是减轻重量。然而，在实际工程应用中，往往是要求多个性能尽量同时达到最优，例如要求质量最小的同时刚度要尽量大，这也就形成了多目标优化问题。近年来，出现了一些比较好的多目标优化算法，如NSGA-II［1］、SPEA2［2］、PAES［3］和MOCell［4］等。经过测试函数的比较，发现MOCell 在解决两目标优化问题时取得了比其他几个算法略好的性能［4］。但是，测试函数［5］是人为构造出来对算法性能进行测试的一类问题，往往与实际工程问题有较大差别，例如个体编码，约束处理，遗传参数的选取等都不尽相同，当要把一个算法应用到实际问题中时，不得不做相应的修改。本文针对机床主轴的参数优化设计问题，在MOCell 算法的基础上采用实数与整数混合编码和NSGA-II 的约束处理机制，基于正交试验理论对MOCell 算法的参数进行优化，利用优化后的MOCell 算法来求解机床主轴优化问题，获得其Pareto 前端，为MOCell 算法求解同时具有实数决策变量和整数决策变量的实际工程问题提供一定的借鉴作用。

1 机床主轴优化模型

机床主轴的示意图［6］如图1 所示。其中da为主轴悬伸段直径，db为主轴左右支撑间的轴径，l为支撑间的跨距，a为主轴悬臂端的长度，d0为主轴内孔直径。

图1 机床主轴示意图

根据材料力学和机械设计的知识，建立的数学模型如下:

主轴体积(mm3):

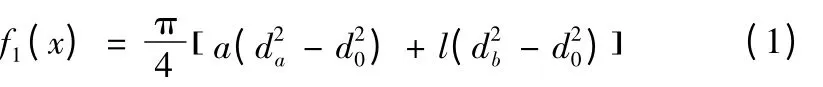
静力F 作用下的挠度(mm):

其中，Ia和Ib分别为主轴悬伸段和左右轴承支撑段的转动惯量。

Ca和Cb分别为右边支撑轴承和左边支撑轴承的刚度。

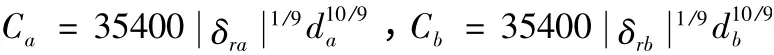
这里，δra和δrb分别为轴承的预载荷。

边界约束条件:

工程设计上对各个直径的比例要求:

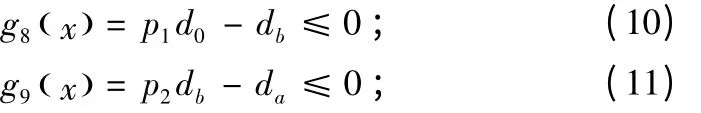
机床主轴端部的最大径向跳动约束:

其中，Δa和Δb分别为右端和左端轴承的径向跳动，Δ 为允许的最大径向跳动。

这个优化问题的决策变量是l、d0、da、db，其中da和db是离散变量，da只能取{80，85，90，95}中的某一个值，db只能取{75，80，85，90}中的某一个值。以上数学模型中的常量［7］给定如下:

2 算法设计

2.1 算法介绍

多目标元胞遗传算法(MOCell)是在元胞遗传算法(cGA)［8］的基础上发展而来的，与cGA 相比，MOCell 的改进在于加入了外部文档，里面存放的是到目前为止算法找到的非支配解，并且引入了反馈机制，即在算法的每一次迭代完成后都选择出一定数量的个体来随机替换掉种群中相等数量的个体。加入外部文档的同时，对外部文档的容量大小做了限制，当找到的非支配解数量超出容量限制时，就会使用拥挤机制来对个体进行筛选，保留拥挤距离大的个体(使用的策略与NSGA-II 中的相同)，这种方法能够保持解集分布的均匀性，有利于得到分布均匀的Pareto 前端。引入反馈机制后，能够充分利用已经找到的较优解来引导种群的进化，有利于提高算法的收敛性能。MOCell 算法的伪代码如表1 所示。

表1 MOCell 算法伪代码

2.2 个体编码设计

在机床主轴优化这个实际问题中，问题的决策变量是l、d0、da、db，其中da和db是离散变量，da只能取{80，85，90，95}中的某一个值，db只能取{75，80，85，90}中的某一个值。因此，不宜使用二进制编码方法。本文采用的方法是将l、d0两个决策变量使用实数编码，组成编码串的前半部分，da、db两个决策变量使用整数编码，组成编码串的后半部分。由于每个编码串对应位置的编码方式相同，因此可以采用单点交叉。

2.3 变异算子设计

个体的编码串是由实数和整数混合编码构成，无论是采用多项式变异还是模拟二进制变异都不能保证编码串的整数编码部分仍为整数。基于此，本文采取的方法如下:

步骤1，将个体编码串的实数编码部分提取出来作为前半部分，将个体编码串的整数编码部分提取出来作为后半部分;

步骤2，对前半部分进行模拟二进制变异(SBX)［9］;

步骤3，对后半部分进行变异。具体做法是，首先分别定义两个数组，将{80，85，90，95}和{75，80，85，90}分别存入其中，然后编写一个0 到3 范围内的随机整数生成函数，每次变异的时候调用这个函数产生一个0 到3 范围内的整数，然后以这个整数为索引找到相应数组里面的具体值;

步骤4，前半部分和后半部分的变异都完成后，将得到的结果重新组合起来构成一个新的编码串，即为得到的变异个体。

2.4 约束处理

为了对问题的约束条件进行处理，采用的方法是当两个个体进行比较的时候，对它们的约束进行检查。如果两个个体都没有违反约束，即它们都是可行解，则直接使用Pareto 支配关系选出较优者;如果一个没有违反约束，而另外一个违反了约束，则没有违反约束的个体较优;如果两个个体都违反了约束，则违反约束少的个体较优。

2.5 正交设计

在遗传算法中，有较多的参数需要进行设置，例如种群大小、交叉概率、变异概率等，遗传参数的选取对算法的性能有较大影响，太差的参数设置甚至会使算法无法收敛。在MOCell 算法中，需要进行设置的参数包括种群大小、邻居大小、反馈个体数量、交叉概率和变异概率。到目前为止，这些参数的设置还没有一个准确的理论依据，大多数情况下都是凭借经验选取的，有一定的盲目性，而正交试验法能够提供一定的指导作用。

“正交试验法”是研究与处理多因素试验的一种科学方法［10］，它是在实际经验与理论认识的基础上，利用一种排列整齐的规格化表——“正交表”来安排试验。由于正交表具有均衡分散，整齐可比的特点，能在考查的范围内，选出代表性强的少数试验条件做到均衡抽样。由于是均衡抽样，能够通过少数的试验次数找到一个较优的试验参数设置。利用这一特点，找到一个最优参数组合来配置MOCell 算法，求解机床主轴优化模型。

用MOCell 算法求解机床主轴优化模型时，有5 个主要因素需要考虑，即种群大小、邻居大小、反馈个体数量、交叉概率和变异概率。其中，种群取较大的值时，多样性会得到一定的提高，但计算消耗会增大，因此一般取为100 到200 之间，交叉概率一般取0.6 到1之间，变异概率一般取0.1 到0.25 之间。为了使试验能够广泛地覆盖整个可能组合，同时试验次数又不至于太多，每个因素取4 个水平。因此选择正交表L16(45)，即5 因素4 水平16 次试验。确定因素水平表如表2 所示，其中，由于使用的是正方形环形拓扑结构的种群，因此种群大小都是平方数。

表2 因素-水平表

2.6 确定评判指标

对算法结果进行评判时，需要一个可靠的评价指标，对算法来说，性能的好坏主要表现在收敛性和分布性两个方面，评价收敛性的指标有GD(世代距离)，评价分布性的指标有Spread(分布指标)，另外还有对收敛性和分布性进行综合评价的指标HV(超体积)［11］。本文选用HV 指标对算法结果做综合评判，此指标的值越大越好。

3 问题求解及结果分析

按照正交表L16(45)和因素-水平表确定试验方案，应用java 编程语言编程进行求解试验，算法的终止条件是25000 次适应度评估，外部文档的大小取为100。为了尽量减少随机误差，每个方案都独立运行20 次，然后将得到的20 组试验结果取平均值，试验方案和结果如表3 所示。

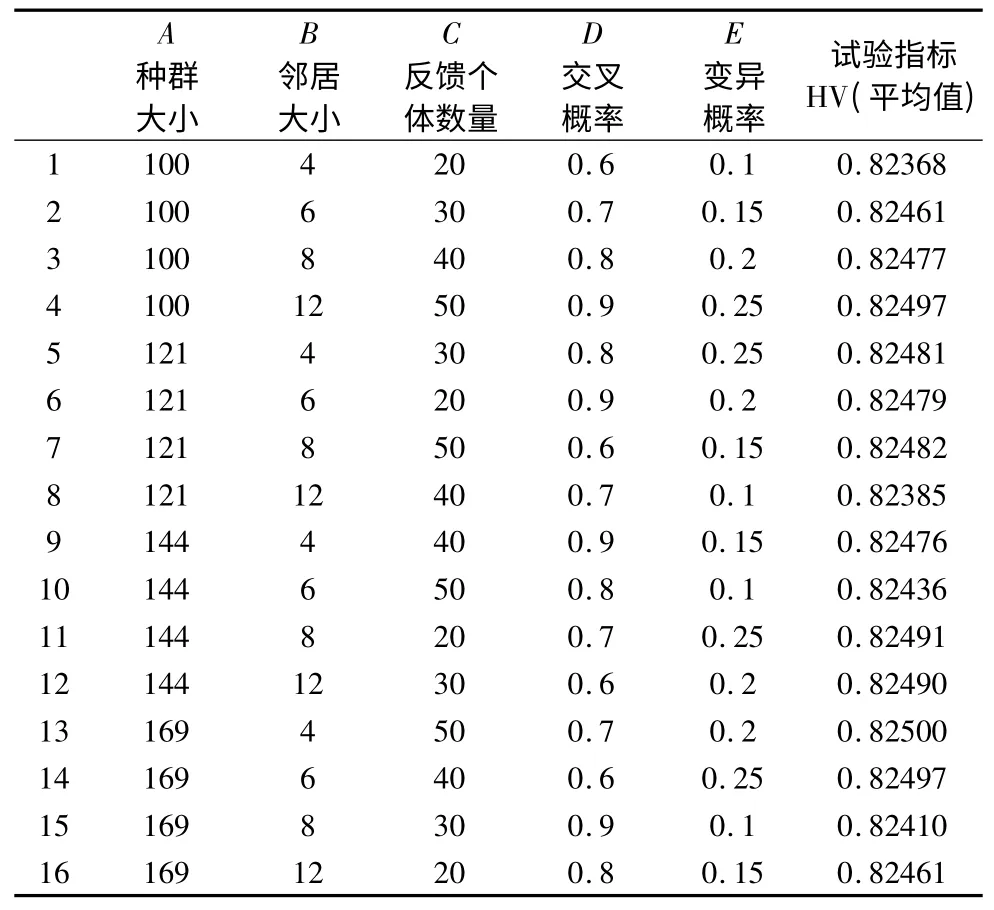
表3 试验方案及结果表

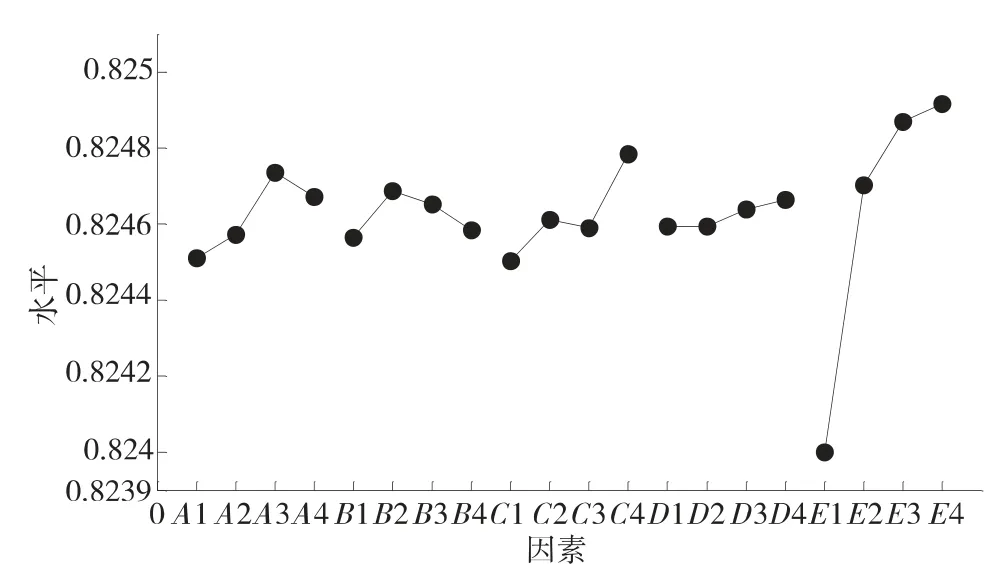
图2 指标-因素图

为了更直观的看出各因素水平的差异，用因素的水平作横坐标，指标HV 作纵坐标，做出指标-因素关系图，如图2 所示。在这个实际问题中，我们需要得到最大的HV 值，因此从图2 中可以很直观的看出A因素取A3，B因素取B2，C因素取C4，D因素取D4，E因素取E4。从而，可以得出此问题的最佳参数配置是A3B2C4D4E4，即种群大小取144，邻居大小取6，反馈个数取50，交叉概率取0.9，变异概率取0.25，按照这种参数配置，重新独立运行程序10 次，得到HV 的平均值是0.83539。从HV 指标来看，与表3 中的结果相比，MOCell 算法的性能确实有所提高。需要说明的是，HV 的数值经过归一化处理，其数值的微小变化会对算法的收敛性和分布性产生较大影响，求出的机床优化模型Pareto 前端如图3 所示。

图3 机床优化模型的Pareto 前端

对于多目标优化问题，我们的主要任务就是找到尽可能接近真实Pareto 前端并且分布尽量均匀和宽广的解集，让决策者根据自己的偏好来选择最合适的解。从图3 可以看出，机床主轴优化模型的Pareto 前端是不连续的，如果使用传统的数学方法来求解会比较困难，但是，使用MOCell 算法能够找到分布非常均匀的Pareto 前端，有利于决策者做出决策。

4 结束语

本文以机床主轴优化设计问题为研究对象，以主轴体积最小和挠度最小为目标，以主轴悬伸段直径、主轴左右支撑间的轴径、支撑间的跨距和主轴内孔直径为决策变量，建立了多目标优化设计数学模型。在对模型进行求解时引入了多目标元胞遗传算法(MOCell)，在MOCell 的基本框架下，结合实际问题的特点，采用了实数-整数混合编码，设计了新的变异方法。为了避免设置遗传参数时的盲目性，使种群大小、邻居大小、反馈个体数量、交叉概率和变异概率的参数设置更加合理，引入了正交试验的思想，经过程序运行试验，找到了较优的参数组合。将通过正交试验获得的参数配置应用到MOCell 算法中对模型进行求解，得到了分布较为均匀的Pareto 前端，有利于决策者根据实际情况做出合适的选择。本文为用MOCell 算法解决实际工程问题做出了尝试，也为其他工程设计人员解决具有整数决策变量和实数决策变量问题时提供了一定的借鉴作用。

［1］Deb K，Pratap A，Agarwal S，et al. A fast and elitist multiobjective genetic algorithm:NSGA-II［J］. Evolutionary Computation，IEEE Transactions on， 2002， 6 (2 ):182 -197.

［2］Zitzler E，Thiele L. Multi-objective evolutionary algorithms:A comparative case study and the strength Pareto approach.IEEE Transactions on Evolutionary Computation，1999，3(4):257 -271.

［3］雷德明，严新平. 多目标智能优化算法及其应用［M］.北京:科学出版社，2009.

［4］Nebro Antonio J，Durillo Juan J，Luna Francisco，Dorronsoro Bernabe，Alba Enrique. MOCell:A cellular genetic algorithm for multiobjective optimization［J］. International Journal of intelligent systems，2009，24(7):726 -746.

［5］Dorronsoro B，Bouvry P. Cellular genetic algorithms without additional parameters［J］. The Journal of Supercomputing，2013，63(3):816 -835.

［6］Ali Riza，Yildiz. A novel hybrid immune algorithm for global optimization in design and manufacturing［J］. Robotics and Computer-Integrated Manufacturing，2009，25 (2):261 -270.

［7］Coello CAC. An empirical study of evolutionary techniques for multiobjective optimization in engineering design［D］.New Orleans:Department of Computer Science，Tulane University，1996.

［8］Alba E，Dorronsoro B. The exploration/ exploitation tradeoff in dynamic cellular genetic algorithms［J］. Evolutionary Computation，IEEE Transactions on， 2005， 9 (2 ):126 -142.

［9］Deb K，Agrawal R B. Simulated binary crossover for continuous search space［J］. Complex Systems，1995，9(2):115 -148.

［10］何为，薛卫东，唐斌. 优化试验设计方法及数据分析［M］.北京:化学工业出版社，2012.

［11］Zitzler E，Thiele L. Multiobjective evolutionary algorithms:a comparative case study and the strength Pareto approach［J］. Evolutionary Computation，1999，3(4):257 -271.