断路器控制系统中的异常数据检测*

陈 力，唐向红

(贵州大学 教育部现代制造技术重点实验室，贵阳 550003)

0 引言

断路器在电网控制系统中起着至关重要的作用，如果它发生了故障，会给整个系统带来十分严重的后果，因此尽量避免故障的发生的工作就显得尤为重要。断路器的控制器是通过传感器来采集大量的连续的不确定的信号，从这些信号中快速的、准确的找出少量的异常的信号，对于整个电网系统而言具有十分重要的意义。

近些年来，人们对于数据挖掘技术的研究越来越深入，数据挖掘技术广泛的应用到各个领域。异常数据检测的基本方法有基于统计的，基于距离的，基于聚类的，基于密度的等。其它的一些数据挖掘技术都是从这些基本的方法中发展出来的。基于距离的检测思想［1-2］由于其算法比较的直观，便于人们的了解和实现而被广泛应用，但是这个方法是在数据集的全部空间属性进行检测，计算的时间复杂度较高，在执行的效率上略有不足。基于聚类的的离群点的检测算法［3-4］的思想是将所有的数据根据数据的属性将数据分成一个个聚类，当某些数据不属于这些聚类的时候，则该对象是基于聚类的离群点，在实际的操作过程中，先对所有的数据进行聚类划分，然后再采用离群点检测算法来挖掘出离群点，由于聚类算法的主要目标并不是发现离群点，只是发现聚类，因此此算法的检测效率很低且针对性较强，适应性不强。Breunning 等提出的一种基于密度的算法［5］，这种算法通过引用局部异常因子(LOF)的概念，LOF 表示的是数据对象之间一定范围内的领域内的分布情况，LOF 的值与所求的数据对象数据分布的疏密程度有关，这个算法的计算复杂度很高，如果所要检测的数据量发生了变化，就需要重新计算所有的数据的LOF 值，因此此算法只适用于静态的数据检测。小波包变换技术［6，7］可以较好的处理非线性信号，但是小波分解存在能量泄露问题，这会严重影响故障信号特征的提取。传统的谱分析技术［8］，利用傅里叶变换得到信号的频率分布，并提取特定频段成份的变化作为特征参数，但这种方法主要适用于对平稳随机信号的处理，由于断路器传感器的工作环境中存在着强烈的电磁干扰，使得传感器测得的数据中包含着大量非线性的成份，因此采用傅里叶变换会产生很大的误差。

近些年来，数据流挖掘技术［9］是信息处理领域的热点话题。而传统的异常点检测算法都将大部分的时间用在了处理正常的数据上，造成时间复杂度很高，并且这些算法不能用到实时的、动态的数据上。为了有效的检测断路器控制系统中的数据流，本文中提出了基于滑动窗口与K-近邻距离的检测算法，利用滑动窗口将数据分成一段段的数据，在时间窗口中利用要检测的数据的有效值来对所有的数据进行剪枝，剔除绝大部分的正常数据，再利用基于K-近邻的检测方法对剩下的数据进行检测。整个算法相对于传统的算法而言，大大的降低了时间复杂度，能适用于短路器控制系统中的实时、动态检测。

1 相关定义

定义1:数据流DS(Datastream)［5］，针对断路器控制系统中传感器采集的数据，数据流是按时间的先后顺序连续产生的序列数据，可以表示为:DS= {(t0，y0)，(t1，y1)，…，(ti，yi)，…}。其中yi是ti时刻所到达的数据。

定义2:滑动时间窗口SW(Sliding window)［11］，在一个时间长度为m的时间序列T中，将其划分为n个时间段的子序列W，W=T0，T1，T2，…Ti，…，Tn-1，每一个时间窗口Ti的宽度都为d。

定义3:数据流的有效值D效，在断路器的控制系统中，传感器采集的信号(电流或电压)，根据这种采集到的谐波信号得到在正常工作的情况下信号的有效值D效，且根据断路器机械设备的特性可以得出基于有效值的一个阈值，用符号EA表示，EA=［D效+D1，D效-D2］.则信号的yi值处于EA的范围内，断路器会正常工作，否则数据点可能为异常数据。

定义4:p的K-距离(K-distance(p))［12］，对于任意的自然数K，定义p的K-距离p和某个对象之间的距离d(p，o)且满足以下的条件:

(1)至少存在K个对象o，，∈D，使d(p，o，)≦d(p，o);

(2)至多存在K-1 个对象o，，∈D，使d(p，o)＜d(p，o);

定义5:p的K-距离邻域［12］给定p的K-distance(p)，p的K-距离邻域包含了所有与p距离不超过Kdistance(p)的对象。

定义6:在当前窗口中，将p的近邻的数据的距离进行排序，到达K-近邻距离的前n个数据为异常点。

2 基于滑动窗口和信号的有效值的阈值EA的剪枝方法

对于数据流DS 而言，异常的数据是占少部分的、离散的，绝大部分是属于正常的数据。因此我们要想办法在所有的数据中快速的剔除那些绝大部分的正常的数据，再对剩下的可能存在的异常的数据进行检测，这样对于整个数据的检测而言会节省很多的时间。

断路器控制系统在实际的运行工程中要检测的参数y值与时间t有关。在这里我们以“电流—时间”为例，时间t是连续的，电流y值是随着时间变化的，是离散的。在正常的工作情况下电流的y值都处在电流的有效值的阈值范围内，但是在某些时候电流的y值会超过这个区域，那么它就有可能是异常点。

在整个数据流的剪枝过程中，会计算出每个数据点的y值与数据的有效值的差值，再查看这个差值是否处在这个阈值范围内，以此为依据来判断这个数据是否可能是异常点。从上面的过程中可以得出整个剪枝的过程的时间复杂度，对于数据量为n的数据，其时间的计算的复杂度为O(2N)。

计算结果的存储:

通过了剪枝过程的剩下的数据，在接下来的K-近邻距离的检测方法中也需要计算每个数据的y值与有效值之间的差值，这样看来，在整个数据的检测过程中会重复计算某些数据的y值与数据的有效值之间的差值，这样会明显的增加整个检测过程的时间复杂度。

为了解决上面所出现的重复计算的时间复杂度，我们可以采用空间换时间的方法来对整个算法过程进行优化，在第一歩的剪枝的过程中将那些可能是异常点的数据的y值与数据的有效值之间的差值，用符号Li表示，通过开辟内存空间保存这些差值，在下一步运用K-近邻的检测方法的时候，在需要用到这些值的时候直接提取出来。通过这种优化，虽然会增加内存空间来存储某些数据的Li值，但是这样会大幅度的减少算法的时间复杂度。

3 基于滑动时间窗口和数据流的有效值的K—距离检测算法SWRK(Sliding Window RMS K—Distance)的描述

基于断路器控制系统中传感器所采集的数据的特性，我们可以根据数据流的有效值和采用滑动窗口来对数据进行在线检测。在整个检测过程中把数据流分成一个个的小段数据，再分别将这些小段数据放到滑动窗口中进行检测，在滑动窗口中首先对这些数据进行一次筛选，剔除其中大部分正常的数据，再对剔除剩下的数据采用基于K-近邻距离的方法再进行一次检测，根据数据的y值到p距离来判断数据是否为异常点。

这里的p数据的y值设定为数据流的有效值。

具体的算法如下:

算法:带滑动窗口的数据检测的SWRK 算法

输入:数据流DS，数据流的有效值D效，正整数K，滑动时间窗口的宽度d。

输出:当前窗口中到达K-近邻距离的前n个数据点过程:

① 扫描数据流并存储当前时间窗口中的数据直到当前窗口满;

② 对当前窗口的数据进行第一次剪枝，并剔除在EA范围内的数据;

③ 将窗口中可能存在的异常点的数据的Li存储在存储空间中;

④ 计算当前时间窗口内可能存在异常的每个数据点的K-距离以及K-距离邻域;

⑤ 调用存储空间中的Li，将其按从大到小的距离进行排序;

⑥ 输出到达K-近邻距离的前n个数据点;

⑦ 时间窗口在时间轴上滑向下一个单元;

⑧ 重复①至⑦，直到检测完所有的数据。

4 实验结果分析

本节通过实验来对SWRK 算法进行精确度和效率的分析。在本节的实验中分别采用了真实数据和模拟数据来对此算法来进行检验。所有的实验实在一台PC 机上完成的，该PC 机的配置如下:CPU 是Inter Pentium G630，2.7GHZ，2G 的内存，操作系统是Windows XP，编程的语言是C++。

4.1 真实数据的来源及SWRK 算法中参数对于算法的影响

为了验证SWRK 算法的有效性和准确性，让其具有说服性，在这里采用在数据挖掘领域大家所公认的数据集KDD CUP 1999。数据集KDD CUP 1999 是网络入侵检测数据集，该数据集大概包括70000000 多个网络连接，每个连接都有41 个特征，且该数据集包括5 个大类，由此可见该数据集是十分庞大的。要对此数据集所有的数据都进行检测，这是不切实际的，也是没必要的。在这里只需要选取其中的部分数据，大约为8 ×103条TCP 连接记录，每条记录选择15 个数值型属性，其中包括连接时间、失败、登陆次数等。

查看SWRK 算法中参数对于算法的影响，主要查看其对于算法准确度和效率的影响。首先查看准确度，准确度的表达式如下:

从上文可知，影响SWRK 算法的参数主要是K和d，首先检验参数K对算法的影响。为了体现实验的准确性，在这里采用控制变量法，设定在不同K值情况下滑动时间窗口的宽度d保持一致，同时选取真实数据中的每103条TCP 记录进行一次检测，实验的结果如图1 所示。

图1 不同K 值时检测的准确度

根据上图可知，当K＜4 时，算法的准确率比较低，当K＞4 时，算法的准确率就会比较高，随着K值的增加，准确度也会随着增加，但是当K值达到一定程度后，准确度又会有所下降。出现这样的情况的原因是因为在K值比较小的时候，数据P的K领域内数据量很少，这样就很难判断这些数据中哪些是正常数据，哪些是异常数据;随着K值的增加，数据P的K领域内的数据量也随着增加，这时就会比较容易的判断出这些数据中的异常点，但是当K值增加到一定程度之后，算法的准确率又会有所下降，这时它会将某些异常数据误判为正常的数据。

检验滑动时间窗口宽度d对于算法SWRK 的影响，在这里主要查看在不同时间窗口宽度的情况下，算法的执行时间的情况。选择的实验数据与检查参数K对算法影响的数据相同，实验的结果如图2 所示:

图2 不同滑动窗口宽度算法的执行时间

从图2 中可以看出，相对于同一个数据量而言，随着时间窗口宽度的变大，整个算法的执行时间会增加。随着时间窗口的宽度的增加，每个时间窗口中的数据量会增加，则要处理的数据量也会随着增加。这样就导致了整个算法的时间会增加。

4.2 针对真实数据检验不同算法的优劣

为了说明SWRK 算法的执行效率，通过与其它两种不同算法的比较可以体现出来。

使用SOMRNN［12］和OPWA［9］算法来对本文提出的SWRK 算法来进行效率的性能测试。其中SOMRNN 算法是基于反K-距离近邻的数据流异常点检测。OPWA 算法是基于多个滑动窗口同步计算的数据流异常点检测。这两个算法的内容都与本文的SWRK 算法有关，比较的有针对性。本次实验的数据与上面实验所用的数据相同，实验结果显示的是在相同数据量的情况下，各种算法所执行的时间，如图3 所示。

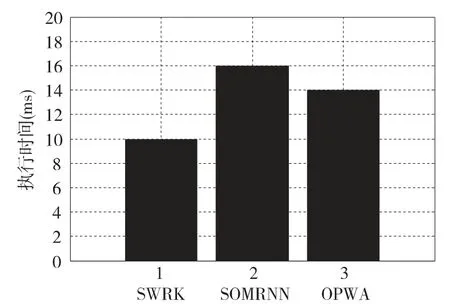
图3 不同算法之间执行时间的比较

从图中可以得出SOMRNN 算法所用的时间最多，SWRK 算法所用的时间最少。SOMRNN 算法所用的时间最多，因为在整个算法的过程中，它绝大部分的时间都用在了计算数据之间的距离上，计算时间复杂度很高。OPWA 算法要比SOMRNN 算法优越，这是因为OPWA 算法在计算数据的聚集程度的时候是同步进行的，虽然这样做会增加内存空间，但是从时间的角度来看，可以为整个算法过程节约大量的时间。这两个算法与本文中的SWRK 算法相比较，在这两个算法执行的过程中没有剪枝过程，因此它们绝大部分的时间都用在了计算正常的数据上面，从而导致了这两个算法的时间复杂度要高于SWRK 算法。

为了体现本文SWRK 算法的准确度，采用在不同K值和不同算法的情况下进行试验，运用SOMRNN 算法和lncLOF 算法和SWRK 算法进行比较。lncLOF 算法动态环境下局部异常的增量挖掘算法。在SOMRNN 算法和lncLOF 算法中都用到了参数K，这样使得本次试验的结果更具有说服力。这里所用到的实验数据与上一个实验所用到的数据相同。实验所得的结果如图4 所示:

从图4 可以看出，本文的SWRK 算法的准确度是最高的。SWRK 算法通过时间滑动窗口，将动态的数据转化成了静态的数据，当窗口中数据满了之后，当前时间窗口的数据量就不会再发生变化，从而就提高了此算法的准确度;在SOMRNN 算法中判断数据是否异常是根据K-近邻个数的趋势来确定的，数据量的变化就影响了整个数据点之间K—距离的变化;lncLOF 算法虽然考虑到了K-距离变化的这个因素，但是数据量的变化任然影响到了整个数据的计算。因为这些因素的影响，本文中所提到的SWRK 算法的准确度高于其他两种算法。

4.3 模拟的实验数据的实验

假设断路器控制系统中要检测的某一电流信号，其表达式如下:

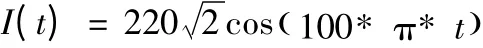
从表达式中可以看出要检测的电流信号的周T=0.02s，频率f=50Hz，在这里选取0s 到0.6s 的波形图，如图5 所示。

图5 I(t)的波形图

从图形可以看出，该波形所显示的数据是正常的数据，不存在异常点。此时认为的给此信号施加一个冲击信号m(t)，是原始的信号产生异常点。此时m(t)信号时一个均值为0，方差为60 的高斯函数，m(t)所发生的区间为［0.2，0.25］，此时电流信号的数据流变为如下所示:

此时信号的波形图如图6 所示。

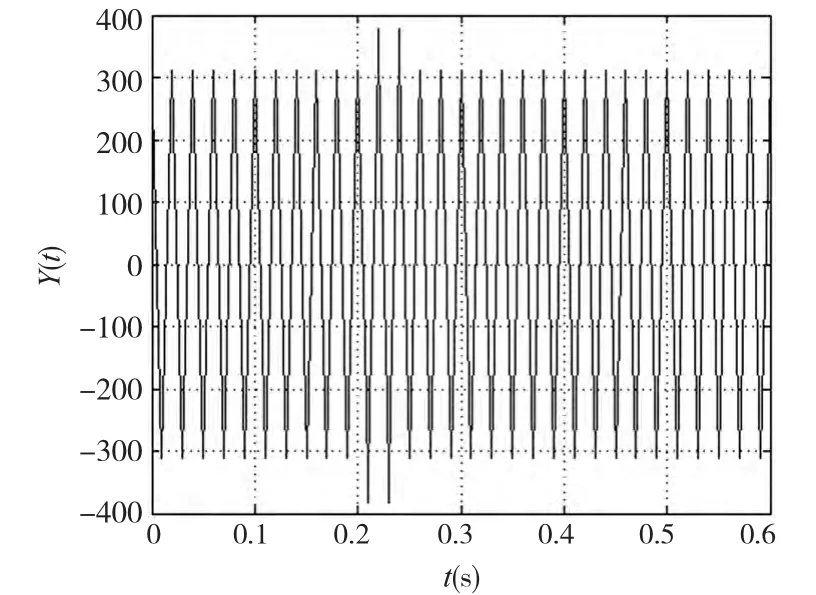
图6 Y(t)的波形图

利用如上图所示的数据流来对本文中的SWRK算法来进行性能检测。在此次试验中运用SOMRNN算法和lncLOF［13］算法来与SWRK 算法相比较，所做的实验是在相同的K值的情况下比较这三个算法的效率。根据4.1 节做所做的关于K值大小对于检测数据的影响，在这里设定K值的大小为6。

运用这三个算法分别对信号Y(t)进行检测，实验的结果如图7 所示。

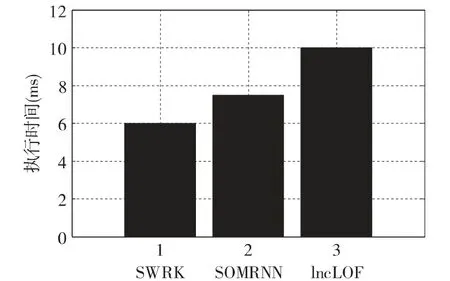
图7 不同算法的执行时间

从上图可知，在这三个算法中，执行效率最低的是lncLOF 算法，执行效率最高的是SWRK 算法。出现这样结果的原因是因为在SOMRNN 算法和lncLOF 算法中整个算法的大部分时间都花在了计算正常数据上面，因此相比较而言SWRK 算法的效率最高。SOMRNN 算法相比于lncLOF 算法而言，它在数据上所计算的时间会低于lncLOF 算法，SOMRNN 算法在检测的过程中，扫描的次数要少于lncLOF 算法。

5 结束语

本文提出了基于滑动时间窗口和K-近邻距离的SWRK 检测算法。该算法是在传统的基于K-近邻距离的检测方法上，利用滑动时间窗口与数据流的有效值，对当前滑动窗口中的所有数据进行剪枝，并在这一过程中保存下一过程中所需要的数据，这样大大的降低了整个算法的时间复杂度。通过实验可以证明SWRK 算法在数据检测的准确度和效率上，都比其它的一些算法优越，因此此算法可以运用到断路器控制系统中的异常数据检测中来。SWRK 算法还存在着一些缺陷，在检测数据的准确度上还有待提高，需要进一步的研究对其优化。

［1］KnorrE，Ng R. Algorithms for mining distance-based outliers in large datasets［C］. Proceedings of the24th VLDB Conference，1998，392 -403.

［2］KnorrE，NgR. A unified approach for mining outliers:properties and computation［C］. Proceedings of Knowledge Discovery and Data Mining (KDD 97)，1997，219 -222.

［3］NgR T，Han J.Efficient and effective clustering methods for spatial data mining［C］. Proceedings of the20th VLDB Conference，1944，144 -155.

［4］GeorgeK，HanEui2Hong (Sam)，VipinK. CHAMEL EON:ahierarchical clustering algorithm using dynamic modeling［J］. IEEE Computer:Special Issue on Data Analysis and M ining，1999，32(8):68 -75.

［5］M Breunig，Hans-Peter Kriegel，R Nget al·LOF:Identifying density-based local outliers ·The ACM SIGMOD 2000 Int’l Confon Management of Data，Dalles，TX，2000.

［6］曾令全，李斌，刘明军.Morlet 小波包络分析在齿轮箱故障诊断中的应用［J］. 组合机床与自动化加工技术2012(7):61 -63，67.

［7］崔勇.小波包变换和RBF 网络在风电机组传动链故障诊断的应用研究［J］. 组合机床与自动化加工技术，2013(10):95 -97.

［8］王欣，周元钧，马齐爽. 基于FFT 和专家系统的BLDCM系统故障检测与识别［J］.北京航空航天大学学报，2013，39(4):564 -568.

［9］周心林，赵雷.数据流上多滑动窗口聚集查询的优化算法［J］.小型微型计算机系统，2013，34(4):774 -777.

［10］ANGIULLI F，FASSETTI F. Very efficient mining of distance-based outliers［C］ / / Proceedings of the Sixteenth ACM Conference on Conference on Information and Knowledge Management. New York:ACM Press，2007.

［11］王伟平，李建中，张冬冬，等.基于滑动窗口的数据流连续JA 查询的处理方法［J］.软件学报，2006，17(4):740-749.

［12］张虑平，梁永欣. 基于反k 近邻的流数据离群点挖掘算法［J］.计算机工程，2009，35(12):11 -13.

［13］杨风召，朱扬勇，施伯乐. IncLOF_动态环境下局部异常的增量挖掘算法［J］. 计算机研究与发展，2004，41(3):447 -484.