用广义高阶导数刻画集值优化ε-严有效解
2014-06-27余丽
余 丽
(宜春学院数学与计算机科学学院,江西宜春336000)
用广义高阶导数刻画集值优化ε-严有效解
余 丽
(宜春学院数学与计算机科学学院,江西宜春336000)
在实赋范线性空间中讨论了集值优化问题ε-严有效解的广义高阶导数型最优性条件.利用广义高阶切集,在没有任何凸性假设下,借助基泛函及ε-严有效解的性质,得到了集值优化问题ε-严有效解的广义高阶导数型的必要和充分条件.
ε-严有效解;广义m-阶切导数;必要条件;充分条件
向量优化理论的逼近解与Ekeland变分原理之间存在着紧密的联系,近年来,对逼近解的研究引起了人们的广泛关注[1-5].文献[4]引进了ε-严有效解的概念,在内部锥-类凸假设下得到了集值优化问题ε-严有效解的标量化定理,ε-Lagrange乘子定理,ε-鞍点定理及ε-对偶定理.另一方面,利用导数研究集值优化问题越来越引起了学者的关注[6-8].文献[8]引进了广义高阶切集和集值映射的广义高阶切导数定义,并得到了集值优化问题取得弱有效解的广义高阶导数型的最优性条件.本文将借助基泛函及ε-严有效解的性质,讨论集值优化问题ε-严有效解的广义高阶导数型的必要和充分条件.
1 基本概念及有关结论
设X,Y和Z为实赋范线性空间,C和D分别是Y和Z中的闭凸点锥,且int C≠Ø,int D≠Ø.设Ø≠M⊂Y,以cl M,int M和cone M分别表示M的闭包、内部和生成锥.一个凸子集B⊂C称为锥C的基,如果0∉cl B且C=cone B.令Bst={φ∈Y*:存在t>0,使得φ(b)≥t,b∈B},并称其为基泛函.
设E是X的子集,F:E→2Y,G:E→2Z.F的有效域为dom(F)={x∈E:F(x)≠Ø}.
定义1.1[4]设Ø≠M⊂Y,B为C的基,ε∈C.点y∈M称为M关于基B的ε-严有效点,记为y∈ε-FE(M,B),如果存在一个零点的邻域U,使得

注1.1[4]对于基B的ε-严有效点定义,(1)式等价于

且根据需要,零点的邻域U可取为或开或闭或凸或均衡.
定义1.2[8]设x∈K⊂X,且v1,…,vm-1∈X,我们称集合
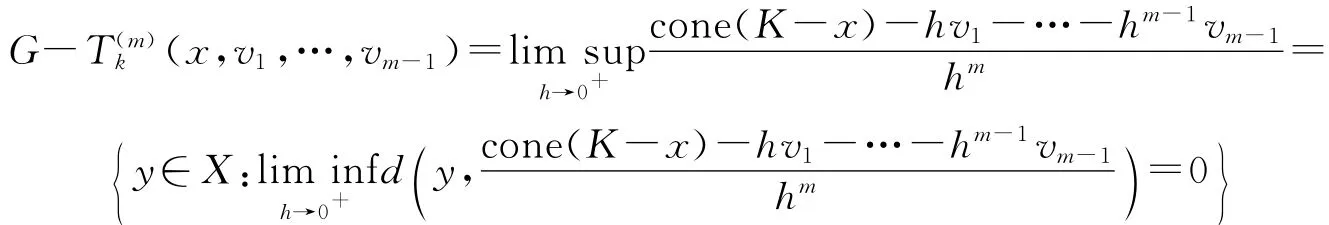
是K在(x,v1,…,vm-1)处的广义m-阶Contingent切锥.
定义1.3[8]设X,Y是赋范线性空间,F:X→2Y是一个集值映射,F是(x,y)∈Graph F关于向量(u1,v1),…,(um-1,vm-1)的广义m-阶Contingent切导数,G-D(m)(x,y,u1,v1,…,um-1,vm-1)是一个从X到Y的集值映射,定义为
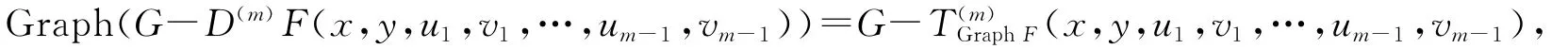
即
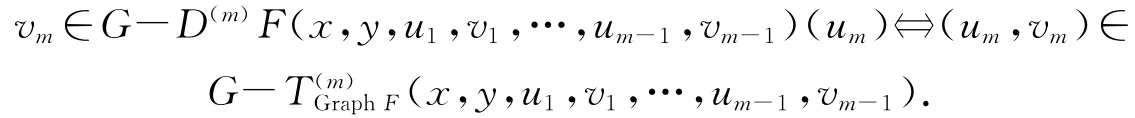
2 最优性条件
考虑如下集值优化问题:
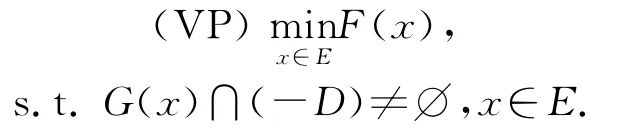
(VP)的可行集表示为
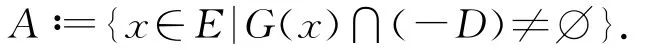
定义2.1 设x0∈A称为(VP)关于基B的ε-严有效解,如果F(x0)∩ε-FE(F(A),B)≠Ø;(x0,y0)称为(VP)关于基B的ε-严有效元,如果x0∈A,且y0∈F(x0)∩ε-FE(F(A),B).
设

记
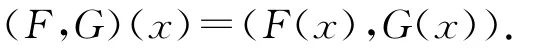
定理2.1 设B为C的有界基,(x0,y0)是(VP)的ε-严有效元,
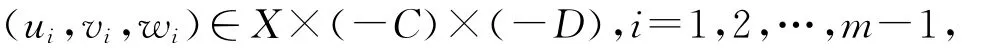
则存在U0∈N(0),使得对于任意的

有
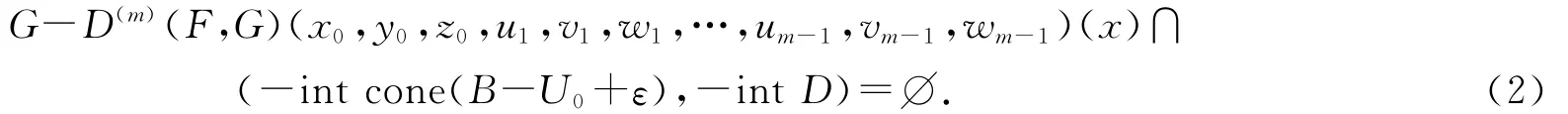
证明 因为(x0,y0)是(VP)的ε-严有效元,于是存在均衡的开凸零点邻域¯U∈N(0),使得
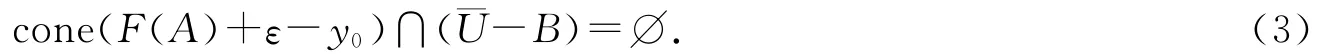
反证法.假设(2)式不成立,则对Y中任意均衡的开凸零点邻域U,存在

使得
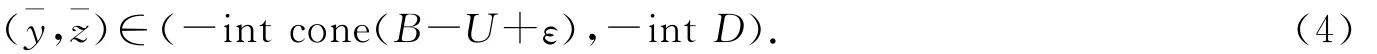
由m-阶广义切导数定义知存在序列{hn},hn→0+,序列
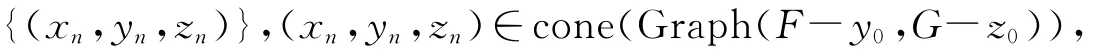
使得

结合(4)—(5)式可知,存在N>0,使得对任意n≥N,有
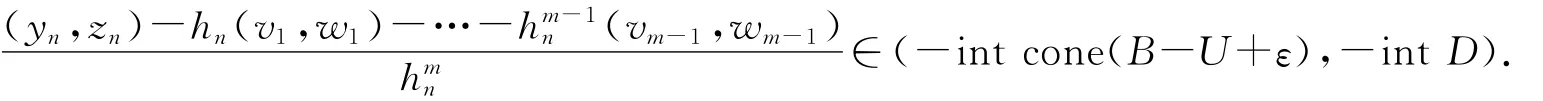
于是
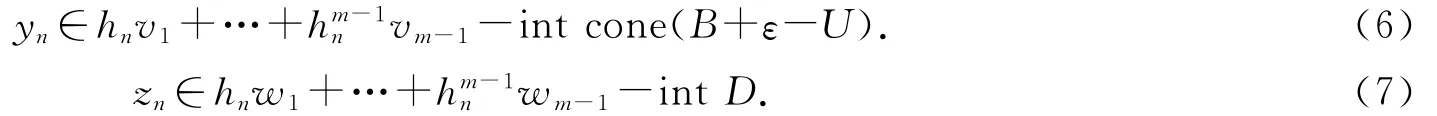
由已知v1,…,vm-1∈-C,w1,…,wm-1∈-D,再由-C及-D为凸锥得
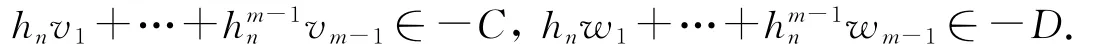
当n>N时,由(6)—(7)式得
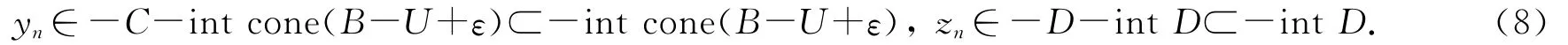
由
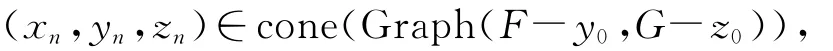
存在(¯xn,¯yn,¯zn),使得
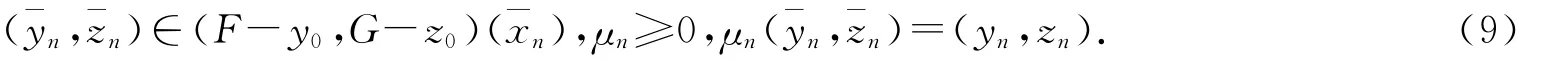
由(8)式知
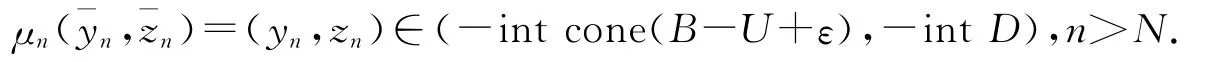
于是当n>N,由
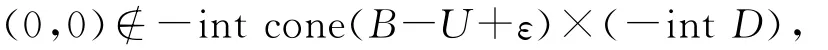
得μn>0及
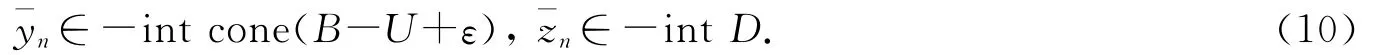
由(9)式知,存在
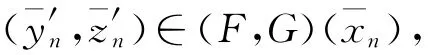
使得

于是
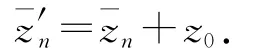
由(10)式及
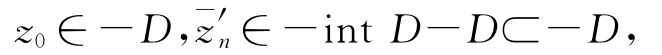
因此
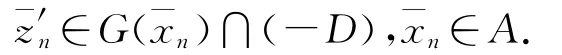
由(11)式,
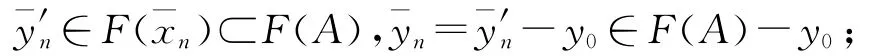
再由(10)式,
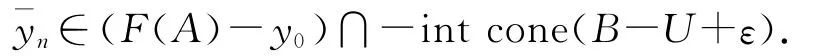
所以
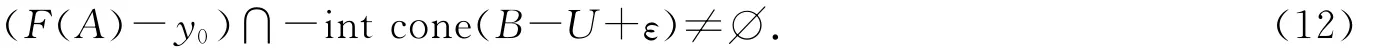
下面证明cone(F(A)-y0+ε)∩(U-B)≠Ø.
先证0∉int cone(U-B-ε).反证法.若0∈int cone(U-B-ε),则由cone(U-B-ε)为凸集知int cone(U-B-ε)=int cl cone(U-B-ε).因为0∈int cl cone(U-B-ε),所以cl cone(U-B-ε)=Y.任取b∈B⊂Y,则存在{tλ(uλ-bλ-ε):λ∈Λ},使得tλ(uλ-bλ-ε)→b.其中tλ≥0,bλ∈B,uλ∈U.因为ε∈C,则存在b1∈B,λ1≥0,使得ε=λ1b1,于是tλ(uλ-bλ-λ1b1)-b→0,因为U是零点邻域,所以存在λ0∈Λ,使得tλ0(uλ0-bλ0-λ1b1)-b=wλ0,其中wλ0∈U,于是tλ0uλ0-wλ0=tλ0bλ0+tλ0λ1b1+b,两边同时除以tλ0+tλ0λ1+1,得

又由U是均衡凸的,有
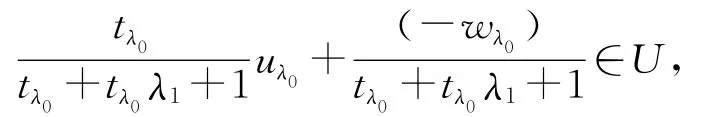
于是
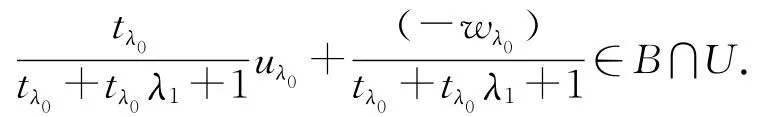
由B是C的有界基及文献[9]中命题2.1知,存在t>0,使得Bst≠Ø.设φ∈Bst,于是有

取Û={y∈Y:|φ(y)|<t},则Û∈N(0)是
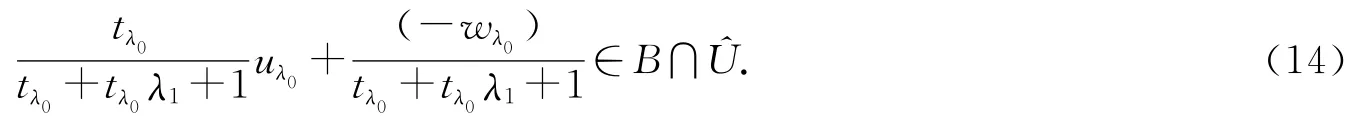
由
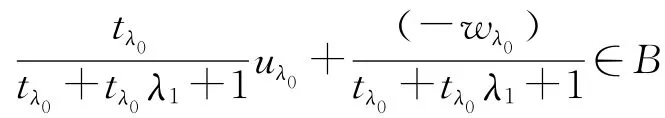
及(13)式得
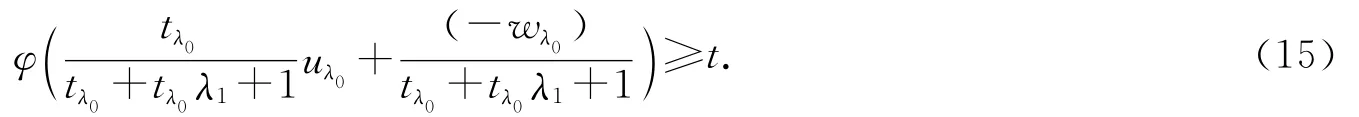
又由
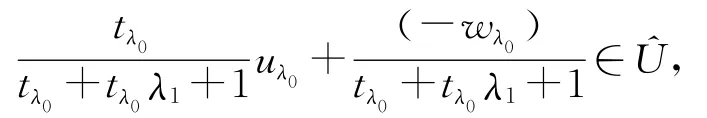
得
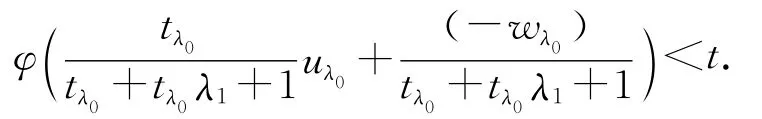
上式与(15)式矛盾.于是

由(12)式知存在
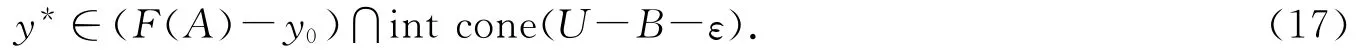
从而
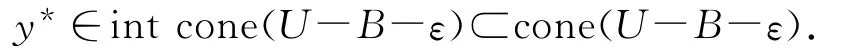
又由(16)式得y*≠0,于是存在λ2>0,b2∈B,u1∈U,使得
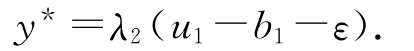
因此
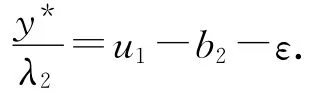
由(17)式得到
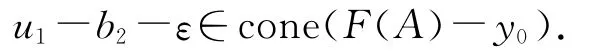
即
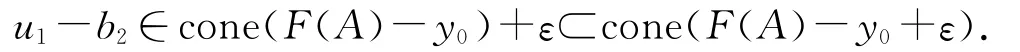
又由
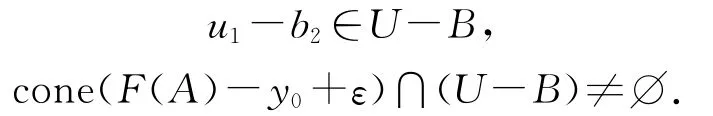
此与(3)式矛盾.
定理2.2 假设以下条件成立:
(ⅰ)(ui,vi,wi)∈{0X}×C×D,i=1,2,…,m-1;
(ⅱ)存在(Γ,L)⊂(cone(B+ε-U)+×D+)\(0Y*,0Z*),使得

并且
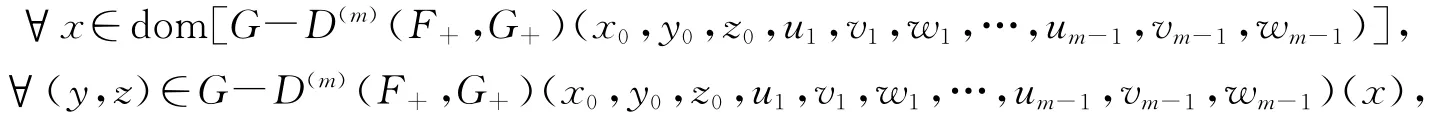
有
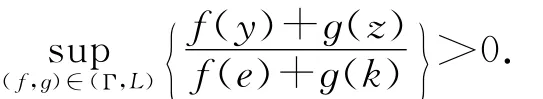
则(x0,y0)是(VP)的ε-严有效解.
证明 反证法.若(x0,y0)不是(VP)的ε-严有效解,则∀U∈N(0),有
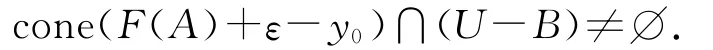
于是存在

使得
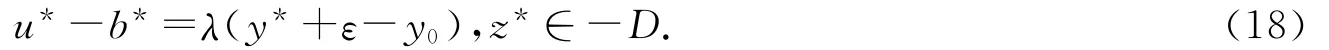
由(18)式知
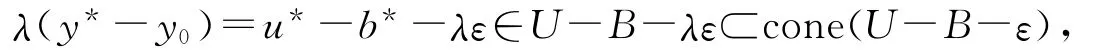
于是

故
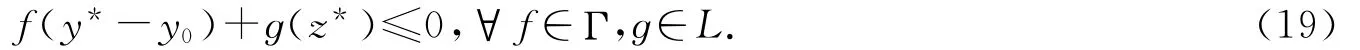
由(19)式和
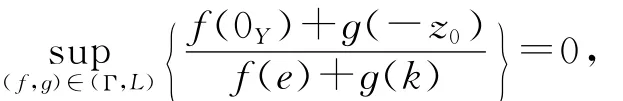
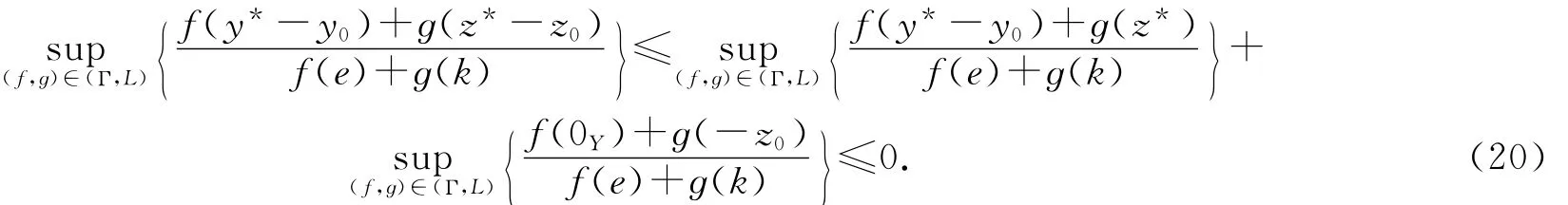
有另一方面,由文献[8]中的命题3.2有
(y*-y0,z*-z0)∈G-D(m)(F+,G))(x0,y0,z0,u1,v1,w1,…,um-1,vm-1,wm-1)(x*-x0).再由条件(ⅱ)有

此与(20)式矛盾.故(x0,y0)是(VP)的ε-严有效解.
[1] RONG W D,MA YI.ε-properly efficient solutions of vector optimization problems with set-valued maps[J].Or Transactions,2000,4(4):21-22.
[2] RONG W D,WU Y N.ε-weak minimal solutions of vector optimization problems with set-valued maps[J].J Optim Theory Appl,2000,106(13):569-579.
[3] LING CHEN.ε-super efficient solutions of vector optimization problems with set-valued maps[J].Or Transactions,2001,5(3):51-56.
[4] LI T Y,XU Y H.ε-strictly efficient solutions of vector optimization problems with set-valued maps[J].Asia-pacific Journal of Operational Research,2007,24(6):841-854.
[5] WANG Q L.ε-strongly efficient solutons for vector optimization with set-valued maps[J].Chin Quart J of Math,2010,25(1):104-109.
[6] LI S J,TEO K L,YANG X Q.Higher-order optimality conditions for set-valued optimization[J].Journal of Optimization Theory and Applications,2008,137(3):533-553.
[7] LI S J,TEO K L,YANG X Q.Higher-order mond-weir duality for set-valued optimization[J].Journal of Computational and Applied Mathematics,2008,217(2):339-349.
[8] WANG Q L,LI S J,TEO K L.Higher-order optimality conditions for weakly efficient solutions in nonconvex set-valued optimization[J].Optimization Letters,2010,4(3):425-437.
[9] CHENG Y H,FU W T.Strong efficiency in a locally convex space[J].Mathematical Methods of Operations Research,1999,50(3):373-384.
The characterizations ofε-strictly efficient solutions of set-valued optimization with generalized higher-order derivatives
YU Li
(Institute of Mathematics and Computer of Science,Yichun University,Yichun 336000,China)
The generalized higher-order derivatives optimality conditions forε-strictly efficient solutions of set-valued optimization problems is discussed in real normed spaces.By virtue of the generalized higher-order tangent sets introduced,without any convexity assumption,by employing the properties of basic functional andε-strictly efficient element,necessary and sufficient conditions are obtained forε-strictly efficient solutions for set-valued optimization problems.
ε-strictly efficient solutions;generalized m-higher-order contingent derivatives;necessary condition;sufficient condition
O 224 [学科代码] 110·74
A
(责任编辑:陶 理)
1000-1832(2014)02-0035-05
10.11672/dbsdzk2014-02-008
2013-04-20
江西省自然科学基金资助项目(20122BAB211004);江西省教育厅科技项目(GJJ13696).
余丽(1980—),女,硕士,讲师,主要从事集值优化及应用研究.
