光电着舰测量设备甲板捷联式视轴稳定系统设计
2014-09-15李雪雷王志乾苏宛新乔彦峰
李雪雷,王志乾,苏宛新,乔彦峰
(1.中科院长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)
光电着舰测量设备是采用光学手段对舰载机着舰过程进行跟踪观测的精密测量设备,它采用自动目标识别[1]和光电跟踪技术对着舰飞行器进行精密跟踪,高精度获取飞行器的下滑航迹角[2]信息及姿态数据,在舰机适配性训练[3]及舰载机定型鉴定中发挥着重要的作用.
作为一种舰机精密光学测量设备,舰体在海浪的作用下产生的随机摇摆,对设备的跟踪性能和测量精度都会产生很大的影响.因此,在对设备进行总体设计时,需要考虑加入惯性系视轴稳定控制系统[4]来克服舰体摇摆对观测视轴[5]指向的影响,保持设备初始跟踪基线的稳定,并提高对目标动态观测时的跟踪精度和测量精度.
1 视轴稳定系统结构选取
光电着舰测量设备采用两轴式光电跟踪仪结构[6],对于两轴式光电跟踪设备而言,实现动基座视轴稳定通常有稳定平台法、视轴捷联稳定法和甲板捷联稳定法.
稳定平台法是首先实现一个独立的抗摇承载平台,该平台具有三轴抗摇的运动机构和伺服控制回路,然后将两轴的光电跟踪设备安放在承载平台上.
视轴捷联稳定法是将惯性传感器(分离的单轴陀螺或组合式多轴陀螺)安装在光电跟踪设备的视轴平台上,直接敏感出在视轴上的惯性系运动分量,通过反馈控制使视轴指向保持稳定.
甲板捷联稳定法是将惯性传感器与甲板平面捷联安装,首先敏感出甲板平面上的舰体摇摆数据,然后通过数学变换,计算出光电设备跟踪轴向上的扰动分量,最后再对光电设备进行抗扰动控制,从而实现跟踪视轴稳定.
考虑到甲板捷联式结构简单,设备安装校准时复杂程度较低,便于采用成熟的整装传感器产品,可借用设备原有的伺服系统工作,且外部数据接口中也常以甲板系作为舰摇数据参考基准,本文在设计视轴稳定系统时选用甲板捷联式直接稳定法.
2 结构描述和姿态角变换公式
系统结构如图1所示,B,M和C为光电着舰测量设备的3个基本组件:B为设备基座,与舰体甲板固连;M为方位转台,绕设备垂直轴旋转,产生方位角A,并承载设备水平轴系O′和观测机构C;C为观测机构,主要是光学成像系统,绕水平轴O′做俯仰运动产生俯仰角E,V为光学系统视准轴.由于水平轴O′被安装在方位转台上,因而水平轴及观测部也同时做方位旋转,视准轴、垂直轴、水平轴校准后交汇于同一原点.
I为惯性系下的姿态角传感器,选用三轴组合惯导平台[7],通过设备基座与舰体甲板捷联.惯导平台的3个敏感轴ox,oy和oz形成右手坐标系,分别敏感出3个自由度的姿态角量.其中ox为舰体横滚角R的敏感轴;oy为舰体艏摇角H 的敏感轴;oz为舰体纵摇角P的敏感轴.
由于光电着舰测量设备采用其方位轴、俯仰轴作为运动轴,因而,要实现视轴姿态控制,应将惯导平台敏感到的姿态角量变换成甲板系下的视轴指向角偏差.
通过分析系统结构的几何关系,引用坐标系旋转矩阵,可推出甲板捷联法的“甲板姿态-视轴指向”姿态角变换公式[8]:
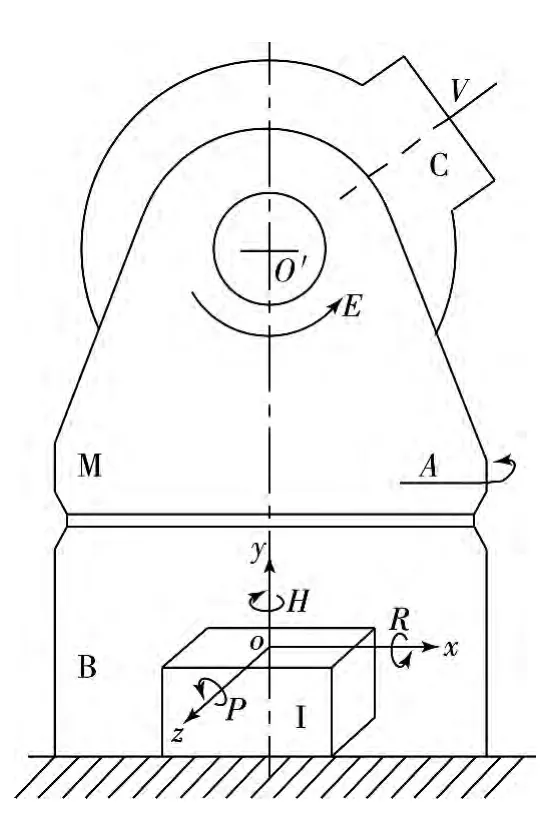
图1 甲板捷联法结构示意图

式中:Ao,Eo分别为目标在站心地平极坐标系[9]下的方位角、俯仰角指向;R,P,H分别为惯导敏感出的舰体/设备摇摆数据横滚角、纵摇角、艏摇角;Ac,Ec分别目标在甲板极坐标系下的方位、俯仰角指向.
各变量要素还应满足如下基准条件:
(1)惯导平台与甲板捷联安装时将传感器上的载体轴向标记刻线OX,OY和OZ与甲板坐标系对准,即OX平行于甲板平面指向舰艏,OY垂直于甲板平面指向天顶,OZ平行于甲板平面指向右舷.
(2)惯导平台的姿态角数据基于站心地平坐标系,即ox,oy和oz敏感轴的惯导数据零位分别指向正北、天顶和正东方向;横摇角R、纵摇角P的正向与其敏感轴间遵从右手定则关系,艏摇H的正向与其敏感轴间遵从左手定则关系.
(3)设备在甲板上安装时经过调平和零位校准,使得设备跟踪轴方位角A的零位指向舰艏方向,俯仰角E的零位平行于甲板平面.
按照(1)式、(2)式求出Ac和Ec后,分别与设备跟踪轴在甲板系下的指向角反馈量A和E做差,即可得出舰体摇摆引起的视轴指向角偏差量.
3 控制系统设计
3.1 控制系统框图
视轴稳定控制系统建立在设备固有的自动跟踪控制回路基础上,和着舰设备的其他光电跟踪功能(如电视自动跟踪)同时工作,方位和俯仰轴都采用相同的控制结构.以方位角跟踪为例,设备伺服控制系统的完整框图如图2所示.图2中视轴稳定系统与设备的其他跟踪控制回路共用速度回路内环,视轴稳定系统的控制量输出作为其他控制方式的前馈量,叠加在速度回路输入端.
为便于分析视轴稳定回路的抗摇隔离性能,根据叠加原理,将视轴稳定回路分离出来,并考虑到方位、俯仰回路的关联性,对视轴稳定控制系统建模(如图3所示).
视轴稳定控制系统由光电着舰测量设备的角速度跟踪内环和惯性系下的视轴姿态控制外环构成(见图3).内环采用旋转编码器作为方位轴、俯仰轴速度反馈元件,以直流力矩电机作为执行元件,控制对象可简化为典型的二阶惯性环节[10],通过闭环控制,实现高带宽高精度的角速度跟踪;外环是姿态稳定环,以组合惯导平台作为姿态角反馈元件,姿态角给定值为站心地平坐标系下的目标指向角.当舰体摇摆时,摇摆运动对视轴形成扰动,最终表现为视轴在甲板坐标系下的指向偏差.该指向偏差被组合惯导平台间接敏感输出(数据需经变换),作为内环的指向误差给定量,内环通过伺服控制实施指向修正,从而实现视轴稳定.
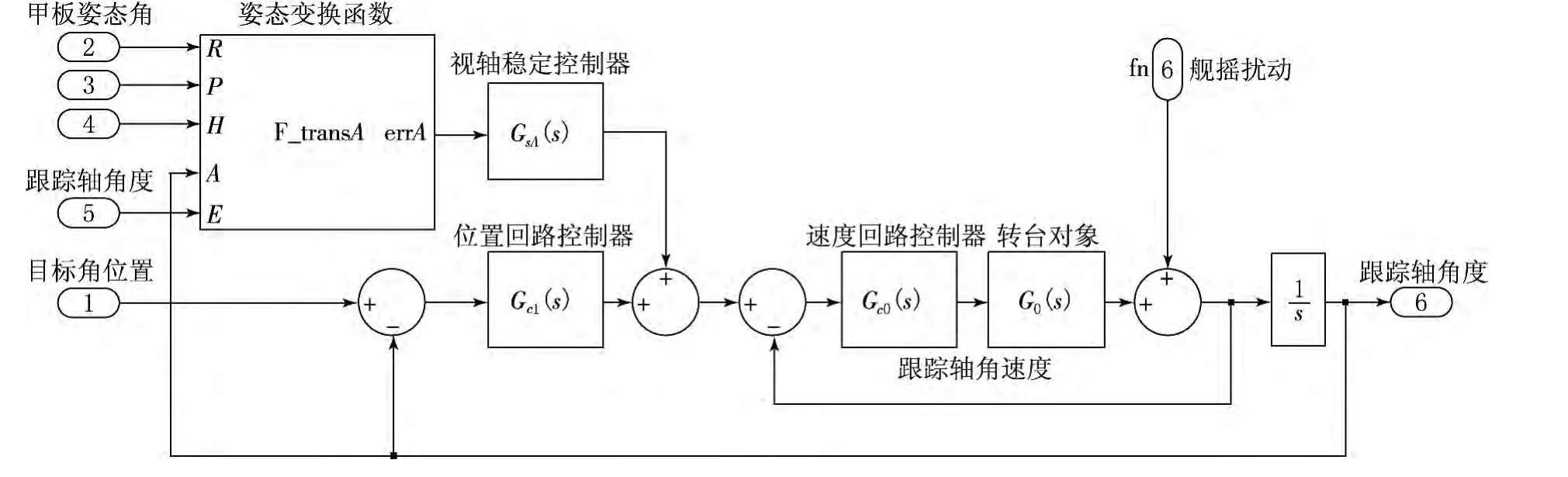
图2 带视轴稳定的方位跟踪控制系统

图3 视轴稳定控制系统
3.2 控制参数选取及仿真
选取控制参数时,首先对系统的直流电机调速模型采用待定系数试验法求解[11],确定出方位、俯仰控制对象的固有参数,然后根据自动控制理论采用频域设计法,对速度回路控制器进行参数设计,使系统开环期望特性满足稳定性和带宽要求.为兼顾系统的其他自动跟踪功能,速度回路选用了二阶滞后-超前校正网络[12],可在有限带宽条件下,提高回路增益,提升速度跟踪性能.
由于海浪引起的舰摇扰动带宽很窄(实际统计约为0.1Hz),远小于速度回路闭环带宽,且视轴姿态稳定回路的隔离比要求也不算太高,故对视轴稳定回路的控制器采用一阶滞后-超前型校正环节.
经对某着舰测量设备的速度开环特性进行实测分析,设计了该视轴稳定控制系统,各环节参数如下:

进行仿真时,根据海上的实际观测经验,以正弦运动模型θ(t)=3sin作为舰摇函数,同时施加于横摇、纵摇和艏摇参量上,通过姿态角变换函数计算出方位、俯仰轴上的扰动速度量作为扰动输入,并模拟出惯导平台的姿态角测量值.用Matlab工具建立系统控制模型,将运动函数代入系统进行仿真,得到系统对地平系零位目标(地平系视轴姿态角给定量为0)进行舰摇稳定控制时,甲板系指向角数据A和E与误差数据err A和err E的输出曲线见图4.

图4 视轴稳定控制回路跟踪性能仿真曲线
视轴稳定系统的舰摇扰动隔离残差率[13]可由err A/(err A+A)与err E/(err E+E)求出,对上述仿真数据的进一步计算可知,系统的舰摇隔离残差率可达0.4%,合隔离度约50dB[14].实际系统中,受惯导的测量精度、数据滞后及系统固有特性的影响,隔离精度会有所下降,可针对具体控制对象的模型特征,通过调整姿态控制器参数或阶次等方式改善稳定回路性能.
4 试验效果
本文的甲板捷联法视轴稳定系统应用于某光电着舰测量设备,选用敏感精度为0.05°的惯导平台作为舰摇姿态传感器,设备在摇摆台上进行了模拟三级海况的视轴稳定试验.试验步骤如下:
(1)将设备在摇摆台上安装校准,完成坐标系对准,使之满足上述3个基准条件;
(2)放置目标源,放置时为不失一般性,选取地平极坐标系下方位角30°、俯仰角-10°作为目标点位;
(3)固定摇摆台,调整设备视轴指向目标源,并使目标源成像在视场中心,保持系统相对静止;
(4)锁止设备跟踪轴,设置摇摆台驱动参数,以摇摆台当前位置为摆动原点,选取摆幅3°、周期9s,相位依次滞后45°的激励源作为三级海况摇摆参数[15]驱动摇摆台,此时视轴稳定系统未工作,目标像点在视场内自由运动,记录图像并判读出目标在视场中的方位脱靶量Δa、俯仰脱靶量Δe,以(Δa,Δe)散点序列连线绘制目标在视场内的相对运动轨迹如图5a;
(5)解除对设备跟踪轴的锁止,开启视轴稳定伺服系统,相同摆动条件下驱动摇摆台,在视轴稳定系统的作用下,视轴指向自动进行动态修正,记录图像并处理,获得目标在视场内的散点轨迹如图5b.

图5 视轴稳定效果试验曲线
对比图5可知,视轴稳定系统工作后,对舰体摇摆带来的指向偏差起到了良好的抑制作用.经对分析试验数据,在三级海况条件下,舰摇隔离误差最大值为5′.
5 结论
甲板捷联式视轴稳定系统结构简单,便于采用成熟的整装传感器产品实现,设备安装标校也相对容易,扰动隔离效果明显,且可借助于光电跟踪设备固有的伺服系统进行控制,是各种舰载、机载、弹载、星载光电跟踪测量设备隔离惯性系扰动的一种很好的选择方案.从仿真和试验也可以看出,系统的视轴稳定隔离误差也与惯导平台的测量精度有关,针对不同的应用环境,可综合考虑性价比因素,选用高精度惯性传感器以获得更好的隔离效果.
[1]黄宗福,韩建涛,陈曾平.天文光电图像序列目标成像特征提取与分析[J].光电工程,2011,38(4):59-65.
[2]罗欢,候明善,刘文风,等.RLV自主着陆航迹设计与控制研究[J].计算机测量与控制,2012,20(3):681-686.
[3]渔翁.舰机适配性对航母设计的影响[J].现代舰船,2006(10):33-36.
[4]王辉化,刘文华,张世英,等.舰载视轴稳定系统的变结构控制研究[J].光电工程,2007,34(3):26-28.
[5]李大成,赵宏斌.基于坐标变换的视轴稳瞄算法[J].光电技术应用,2011,26(2):5-8.
[6]贾庆莲,乔彦峰,邓文渊.光电经纬仪的粒子——卡尔曼联合目标跟踪算法及仿真[J].光电技术应用,2007,22(2):66-70.
[7]张国良,曾静.组合导航原理与技术[M].西安:西安交通大学出版社,2008:31-37.
[8]方成一,王振旺.舰载雷达天线电子稳定方程的推导方法[J].雷达与对抗,1999(2):68-74.
[9]马媛,张成.惯性导航中的坐标变换研究[OL].[2009-02-05].中国科技论文在线,Http://www.paper.edu.cn/releasepaper/content/200902-129.
[10]王显正,陈正航,王旭永.控制理论基础[M].北京:科学出版社,2000:154-170.
[11]王艳颖,王珍,郭丽环.直流电动机传递函数测定的实验研究[J].实验技术与管理,2008,25(8):38-40.
[12]尾形克彦.现代控制工程[M].北京:电子工业出版社,2003:388-415.
[13]孙辉,郎小龙,李志强,等.动载体光电平台视轴稳定精度的检测[J].光学精密工程,2011,19(9):2131-2137.
[14]何荣贤,蒋军.大型船载卫通伺服随动系统船摇隔离度[J].陕西工学院学报,2005,21(2):8-10.
[15]周云华,彭松江,邱群先,等.舰船海况模拟平台等效摇摆参数研究[J].舰船科学技术,2013,35(9):71-74.
