对一道高考理综试题的多种解法分析
2014-06-27林榕郑伟
林 榕 郑 伟
(沈阳师范大学物理科学与技术学院 辽宁 沈阳 110034)
题目:(2013年高考辽宁省理综卷新课第25题)一长木板在水平地面上运动,在t=0时刻将以相对于地面静止的物块轻放到地板上,以后木板运动的速度-时间图像如图1所示.已知物块与木板的质量相等,物块与木板间及木板与地面间均有摩擦,物块与木板间的最大静摩擦力等于滑动摩擦力,且物块始终在木板上.取重力加速度的大小g=10 m/s2,求
(1)物块与木板间、木板与地面间的动摩擦因数;
(2)从t=0时刻到物块与木板均停止运动时,物块相对于木板的位移的大小.
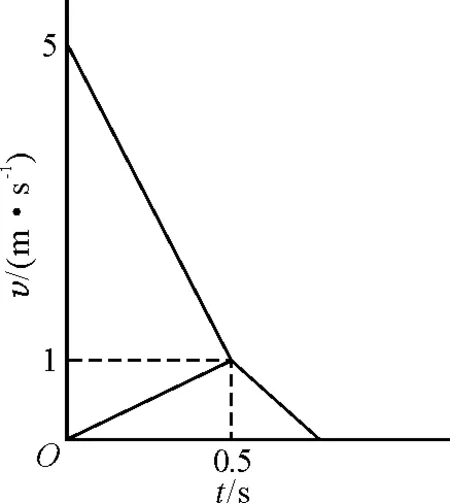
图1
解析:第(1)问求物块与木板间、木板与地面间的动摩擦因数;
由图可设
v0=5 m/sv1=1 m/st1=0.5 s
设物块与木板间、木板与地面间的动摩擦因数分别为μ1,μ2.
解法1:根据运动学方程和牛顿第二定律,由所给的图1,在t0=0→t1=0.5 s时间段,可得
物块加速过程
木板减速过程
由牛顿第二定律得
μ1mg=ma1
μ1mg+2μ2·mg=ma2
联立解得
μ1=0.2
μ2=0.3
解法2:根据动量定理
对物块
μ1mgt1=mv1
对木板
(2μ2·mg+μ1mg)t1=mv0-mv1
联立解得
μ1=0.2
μ2=0.3
解法3:根据运动学方程和动能定理,考察在
t0=0→t1=0.5 s时间段,有
对物块
解得
对木板
解得
μ2=0.3
第(2)问求从t=0时刻到物块与木板均停止运动时,物块相对于木板的位移的大小.
解法1:根据运动学方程和牛顿第二定律
当t>t1=0.5 s后,物块仍然相对木板滑动,且以加速度a1做减速运动,其运动时间也是t=0.5 s.
对物块
f=ma1
对木板
f=μ1mg
物块相对地的总位移
或
或
木板相对地的总位移
或
或
其中
物块相对于木板的位移的大小为
s=s2-s1
联立以上诸式,解得
s=1.125 m
解法2:根据动能定理
对物块
或
物块相对地的位移
对木板
木板相对地的位移
联立,解得
s=s2-s1=1.125 m
解法3:相对位移法
前半段,t=0 ~t1=0.5 s.
物块相对地的位移
木板相对地的位移
前半段物块相对于木板的位移

后半段,t1=0.5 s至物块、木板都停止运动.
物块相对地的位移
木板相对地的位移
或
后半段物块相对于木板的位移
Δs后=s1″-s2″=0.125 m
所以,物块相对于木板的总位移的大小为
s=|Δs前+Δs后|=|-1.25+0.125|=1.125 m
解法4:相对加速度法
前半段,t=0 ~t1=0.5 s.
物块加速度大小
木板加速度大小
所以,物块相对木板的加速度大小为
a相1=a1+a2=10 m/s2
前半段物块相对于木板的位移

中段,t=0.5 s至t=0.75 s(此时木板停止了运动).
物块相对木板的加速度大小为

中段物块相对于木板的位移

则可求得
Δs中=0.062 5 m
后段,t=0.75 s至t=1.0 s(此时物块停止了运动).
物块相对木板的加速度大小为
a相3=a1=2 m/s2
后段物块相对于木板的位移
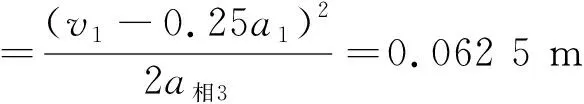
所以,物块相对于木板的总位移的大小为
s=|Δs前+Δs中+Δs后|
代入数据得
s=|-1.25+0.062 5+0.062 5| m=1.125 m
解法5:几何方法
由木板的图2v-t曲线可知,木板相对地的位移大小就是曲线下所围图形ABCOA的面积.
而物块在0~0.5 s以及0.5 s~1.0 s两段运动均满足
f=μ1mg=ma1
a1=μ1g=2 m/s2
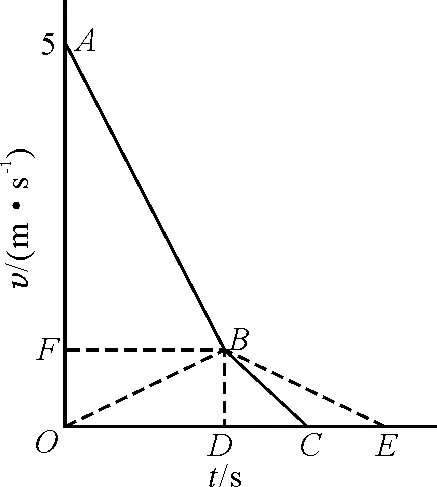
图2
即前半段做匀加速运动,后半段做匀减速运动,所以其v-t曲线为OBE,与横轴围成一个等腰三角形,其面积即为物块相对地的位移大小.
对木板后半段加速度由下式确定
即
木板后半段运动时间为
在以上条件基础上,即已知了
t1=tOD=0.5 s
t=tDC=0.25 s
t′=tCE=0.25 s
OA=5 m/sOF=1 m/s
可以通过以下几种组合方式求出物块相对木板的位移大小.
方式1:
s=SOABCO-SOBCO
其中
SOBCO=2SOBDO=
所以物块相对木板的位移大小为
s=SOABCO-SOBCO=1.125 m
方式2:
s=SABF+SBCD
其中
所以物块相对木板的位移大小为
s=SABF+SBCD=(1.0+0.125) m=1.125 m
方式3:
s=SOAB-SBCE
其中
所以物块相对木板的位移大小为
s=SOAB-SBCE=(1.25-0.125) m=1.125 m
小结:以上将第(1)问、第(2)问分别用不同解法解得相同结果,它们再组合起来可以构成至少21种完整的题解.试题的信息及考察结果启示我们:在平时的物理教学和备考复习中,应该强化物理概念的意义建构,突出物理过程、物理情境的分析,正确建立物理模型及相关物理方程,应是广大物理教师努力的重点.加强基础训练,培养学生理解能力、推理能力、分析综合能力和应用数学解决物理问题的能力也是物理教学的重要任务.
鉴于此,我们要有意识地创设一些物理问题,引发学生深层思维实际物理情境,指导学生进行分析建模,要细化物理基本概念基本规律和基本思维方法的教育;要重视应用数学工具解决物理问题的基本运算训练.
