电子型超导材料的超流密度响应

王 宏

(大同煤炭职业技术学院 山西 大同 037003)

1 高温超导的发现

人们将低温下直流电阻消失的现象称为超导电性，具有超导电性的材料称超导体.1911年4月8日，荷兰莱顿大学的卡末林·昂内斯(H. Kamerlingh Onnes)发现，用液氦将汞的温度降到4.3 K时，汞的电阻突然消失，这是人类历史上首次发现超导现象．

超导体的基本属性由以下3个特征表示.

(1)超导态是一种新的凝聚态．

(2)超导体中准粒子激发存在能隙Δ，即在超导相中激发出一个准粒子至少需要Δ能量．

(3)超导体中存在迈斯纳效应，即在超导态下磁场不能透入宏观样品内部，超导体对于弱场是完全逆磁体．

超导体除了具有以上三个基本特征外，在此之后人们还发现了超导穿透深度(伦敦穿透深度)、超导相干长度、超导体的同位素效应、压力效应、宏观量子效应、隧道效应、交流感应台阶效应、超导邻近效应等．在超导产生机制上，著名的BCS理论提出，超导现象看作一种宏观量子效应，它认为电子间的直接相互作用是相互排斥的库仑力．但如果仅仅存在库仑力直接作用的话，电子不能形成配对，电子间还存在以晶格振动(声子)为媒介的间接相互作用．这种相互作用是吸引的，称为有效吸引，正是这种吸引作用导致了金属中自旋和动量相反的电子可以配对形成“库珀对”．“库珀对”在晶格当中可以无损耗的运动，形成超导电流．

目前已发现有一半的金属元素和成百上千种合金与化合物超导体，但是它们的超导转变温度Tc较低，直到20世纪80年代中期Tc未能突破30 K大关．1986年Alex Müllerh和George Bednoz首次发现铜氧钙钛陶瓷La-Ba-Cu-O化合物中的高温超导现象，转变温度为35 K，结果很快被同行证实和加以改进，并在掺入二价金属M(Ba，Sr等)的La2-xMxCuO4-y化合物体系中获得了Tc高于40 K的超导转变温度．1987年2月，美国的朱经武[1]教授研究组和我国的赵忠贤[2]教授研究组先后独立地在YBa2Cu3O7-y(后简称Y-123)[3]化合物中发现了Tc≥90 K的氧化物高温超导体，使超导体研究首次进入了液氮温区．1988年初，人们又发现了另外两组具有更高转变温度Tc的铜氧化物的超导体：Bi2Sr2Ca2Cu3O10+x(Bi-2223)，其Tc=110 K[4]；Tl2Ba2Ca2Cu3O10(Tl-2223)，其超导转变温度高达Tc=125 K[5]．迄今为止被公认的最高的超导转变温度是朱经武研究组[6]在HgBa2Ca2Cu3O8+x(Hg-1223)化合物中测量得到的，其中转变温度Tc=133 K，加压力甚至可使Tc提升到160 K以上．自从Alex Müllerh与George Bednoz新发现的铜氧化合物问世以来，超导转变温度屡破纪录，在不到两年的时间内Tc已提高了4～5倍，进入了便于工作的液氮温区，其临界磁场也很高(见表1)，为超导电性的研究和应用开辟了一个新时期．

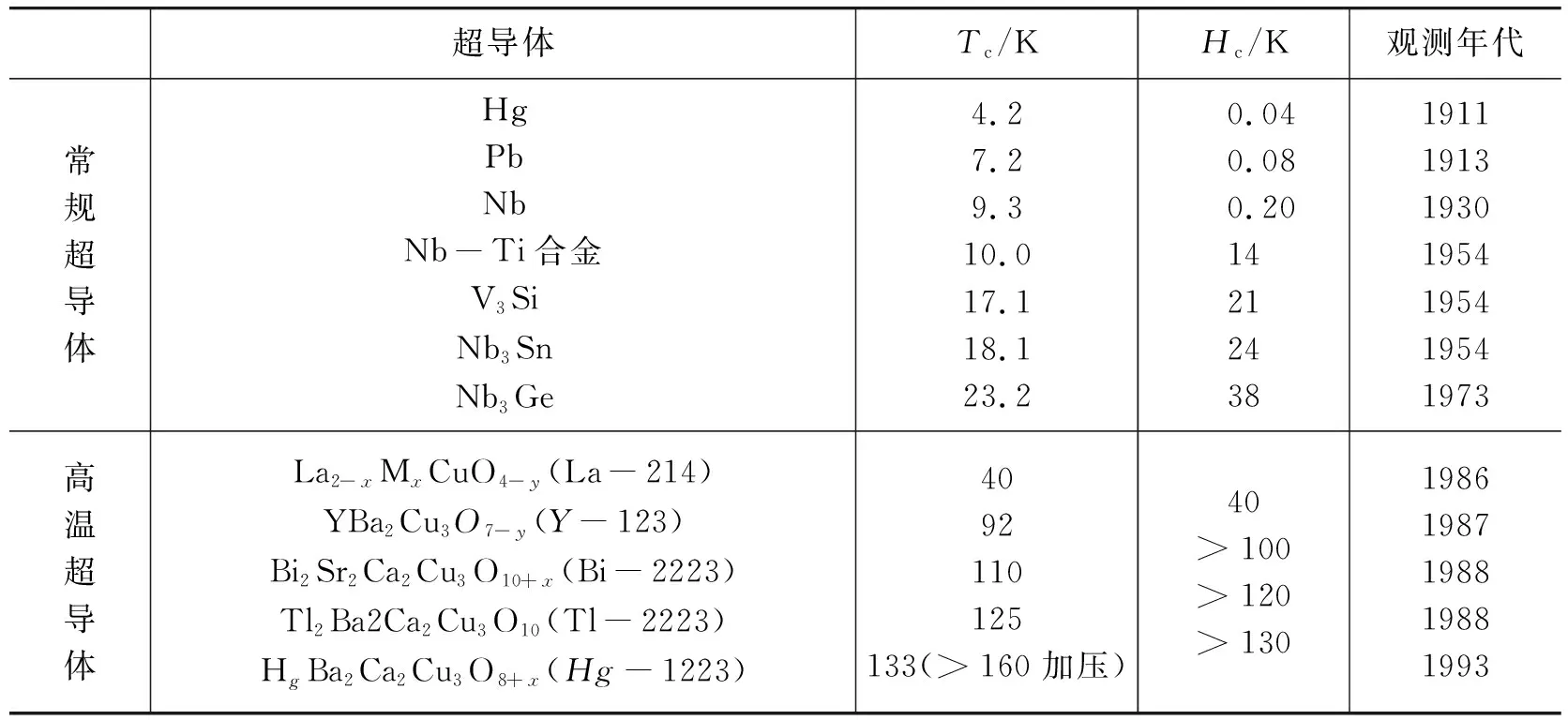
表1 超导转变温度和临界磁场提高的编年表

2 电子掺杂型高温超导的微观模型及t-t′-t′′-J模型

高温超导体是在钙钛矿结构铜氧化物中发现的，它们绝大多数是通过部分替代绝缘体的母体化合物中的化学元素得到的[7]．元素替代的一个主要作用就是引入自由载流子，也有一些是靠缺氧或富氧引进导电载流子．这种元素替代或缺、富氧过程被称为掺杂．典型的母体化合物包括La2CuO4和YBa2Cu3O6，都是反铁磁绝缘体．最早发现的两种高温超导体就是通过对这两种绝缘体掺杂得到的．掺杂有两种情况：一是在母体中引入空穴载流子，由此得到的超导体称之为空穴型超导体；二是在母体中引入电子载流子，由此得到的超导体称之为电子型超导体，目前发现的高温超导体绝大多数是空穴型的．

高温超导体有数十种，它们具有不同的晶体化学结构，但都是各向异性很强的二维材料，存在由Cu和O原子组成的CuO2平面(见图1)．在存在自由载流子的情况下高温超导体沿CuO2平面方向的导电性能比垂直于平面方向的导电性能强得多，一般高2～4个数量级．CuO2平面上的电子态是决定高温超导体的输运性质和低能热激发的主要因素，这点已得到能带计算和大量实验测量的证实，是分析高温超导现象的一个基本出发点．

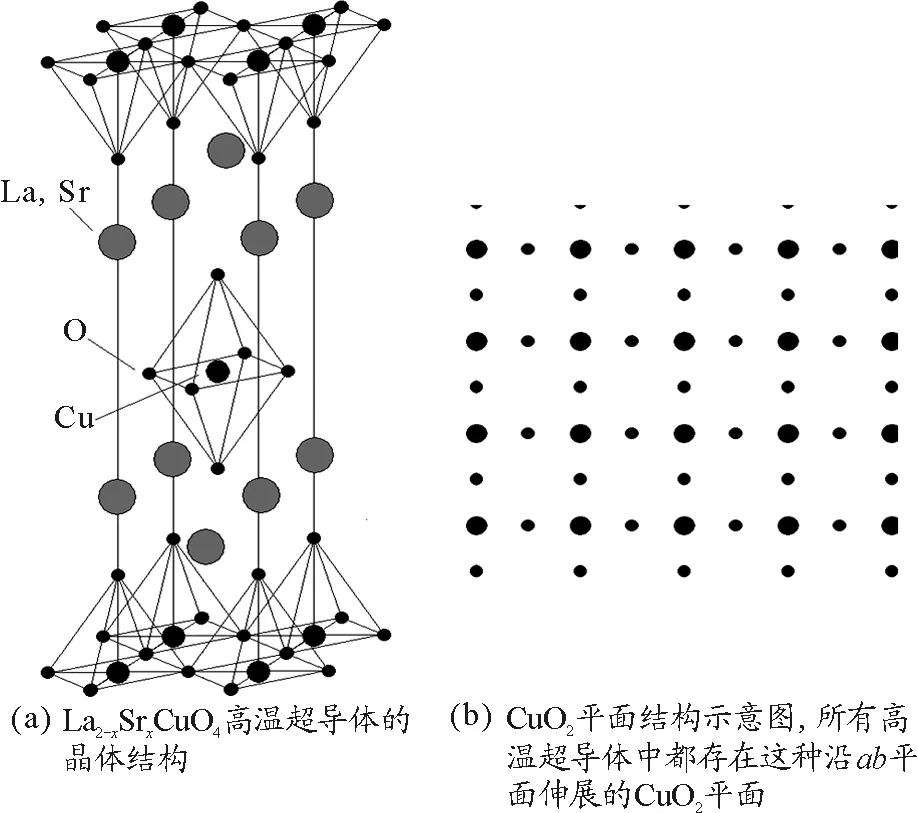
图1

高温超导研究中常用的t-t′-t″-J模型[8]的哈密顿量可以写成如下形式

(1)

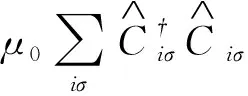
(2)

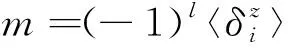
最终得到能带为

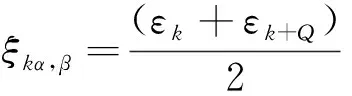
评价：1.满足“差一点饱”的客人。2.未曾试过的菜品可以先来试试鲜。3.满足减肥的顾客，或者体力工作者对餐量的不同需求。

(3)

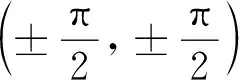
3 电子掺杂型超导体的超流响应

超流密度是描述超流响应的一个重要物理量，是连接超导微观机理与宏观电磁学的一个重要参量．超流密度反比于磁穿透深度的平方，是伦敦方程的一个重要推论，它将超导流密度Js与电磁场矢势A直接联系到了一起．在线性响应理论中，系统对外加电磁场的响应由久保公式决定[9]

(4)

式中Kμν是电流Jμ对外场Aν的响应函数，然而在超导态中，电流密度可以表述为如下形式

(5)

引入流-流关联函数

(6)

代入后，响应函数变为如下式子

(7)

经归一化变换后，最终写成这样的形式

(8)

其中

(9)

(10)

这样我们就得到了在线性近似下的电磁响应函数，原则只在外场H→0的极限下成立．对于s波超导体，由于存在有限能隙，这些公式在有限但低场下也是可以使用的．但对于dx2-y2波超导体，由于存在能隙节点，超导体对磁场的非线性响应在低温下会变得比较重要．同时，由于沿着能隙节点方向的有效相干长度是无穷大，非定域效应在低温下也会变得比较重要．这些效应对低温下的电磁响应函数都会有影响．经过最终化简式(8)可求出Πμν在(ω=0,q→0)极限下的值为

(9)

4 结果

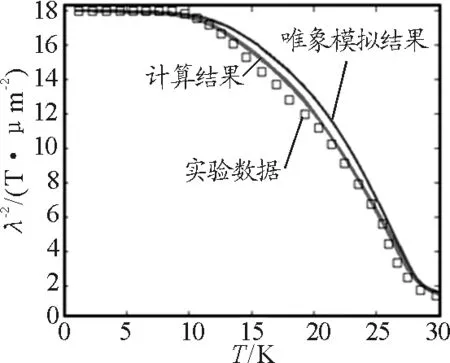
图2 欠掺杂下的超流密度图、下边曲线为计算的结果，

□为实验数据，上边曲线为唯象方法拟合的结果

图3给出了最佳掺杂下计算值与实验值之间的对比和过掺杂下的与实验数据的对比．通过对三组掺杂的计算，不仅和实验数据进行了比较还和早期用唯象方法研究的结论也进行了比较，通过比较发现，计算结果与实验数据符合的很好，这样就解释了之前的推导是正确的，从而证明了电子掺杂型铜氧化物高温超导材料的电子配对对称性为dx2-y2波，达到了预期目的．

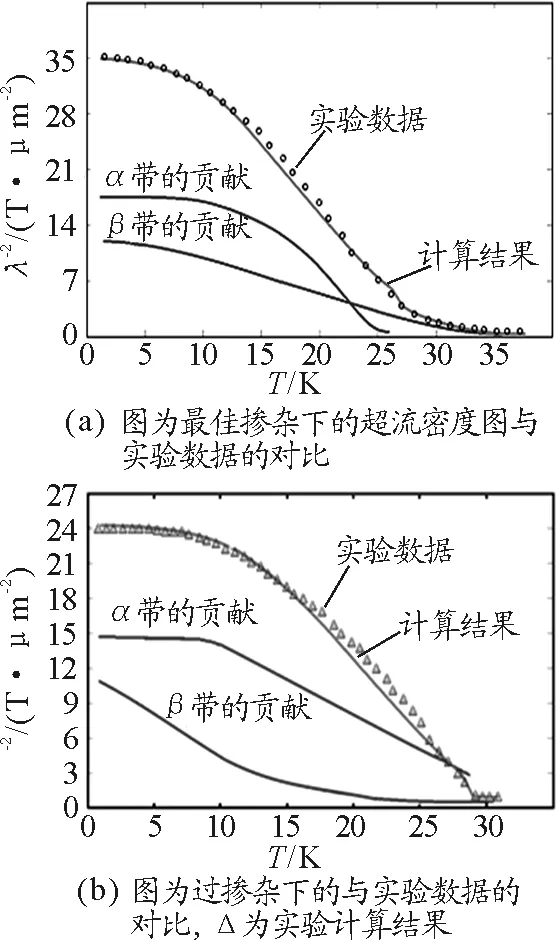
图3

5 结论

通过对电子掺杂型超导材料建立的弱耦合两带模型为基础，明确了在微观上电子掺杂的超导材料的两带耦合作用为反铁磁相互作用，并对这两个带分别进行了超流密度的计算，确定了系统的总的超流密度为上下两个带的共同作用的结果，因此得到电子掺杂型铜氧化物高温超导材料的电子配对对称性具有dx2-y2波对称性．在此基础上，还分别计算了在掺杂量分别为χ=0.124的欠掺杂情况、χ=0.131的最佳掺杂情况和χ=0.152的过掺杂情况下的超流密度，并对这三种掺杂量下的超流密度随温度T的变化关系分别与实验数据做了对比，能够比较好的符合实验数据，这个结果与之前以两带模型为基础用唯象的方法求得的结果是一致的．

通过对不同掺杂量下超流密度随温度变化关系，可以明确在微观上对电子掺杂型超导体用弱反铁磁作用耦合两带模型的描述是正确的，而且肯定了电子掺杂型超导体中电子配对对称性为dx2-y2波对称性．最终用不同掺杂量下计算的超流密度随温度变化关系与实验观察的数据比较，以及和早期用唯象方法建立两带模型求得的结果都是一致的．这不仅为进一步研究电子掺杂型超导体的微观导电机制提供了有力的理论支持，还为对电子掺杂型铜氧化物高温超导材料的电子配对对称性提供了理论依据，明确了电子掺杂型高温超导材料超导电性的微观导电机制．

参考文献

1 Chu.C.W,et al.Superconductivity Up to 114 K in The Bi-Al-Ca-Sr-Cu-O Compound System Without Rare-Earth Elements.Phys.Rev.Lett,1988,60 (10):941～943

2 赵忠贤,等. Ba-Y-Cu氧化物液氮温区的超导电性.科学通报,1987,32:412～413

3 Xiang.T,Wheatley.J.M.Superfluid Anisotropy in YBCO:Evidence for Pair Tunneling Superconductivity.Phys.Rev.Lett,1996,76 (1):134～137

4 Sheng.Z.Z,et al.Superconductivity at 90 K in the Tl-Ba-Cu-O System.Phys.Rev.Lett,1988,60(10):937～940

5 Tokura.Y,Takagi.H,Uchida.S,et al.A Superconducting Copper Oxide Compound with Electrons as the Charge Carriers.Nature,1989,337(10):345～347

6 Levi.B.G.There's Still Some Resistance to Reports of Extra-High TcSuperconductors.Phys.Today.1994,47(2):17～21

7 向涛.d波超导体.北京:科学出版社,2007,511(063487):235～236

8 Kusko.C,Markiewicz.R.S,Lindroos M.Bansil1 A.Fermi Surface Evolution and Collapse of the Mott Pseudogap in Nd2-xCexCuO4±δ.Phys.Rev.B.2002,66(14):140513～140517

9 Mahan.G.D.Many-Particle Physics.Plenum Press.1990,813～818