Matlab在电路分析教学中的应用

拉巴次仁

(西藏大学理学院 西藏 拉萨 850000)

Matlab是美国Mathworks 公司推出的一套集数值分析、矩阵运算、信号处理和图形显示于一体的高性能软件，它已经成为数学计算、数据分析与可视化、信号处理和仿真等领域首先的工具软件．动态电路分析的基本方法是建立微分方程，然后用高等数学知识求解微分方程，最后得到电压电流响应的表达式，然而动态电路分析中，最困难的事情是求解微分方程，即便是求出微分方程的解，结果中也看不出其物理含义．文章通过几个实例介绍了Matlab在电路分析教学中的应用，帮助学生更好更快地了解电路特性和掌握电路原理．

1 利用Matlab求解RLC电路的响应方程，并把结果可视化

【例1】图1(a)所示的RC电路中的开关连接至1端已经很久，在t=0时，开关迅速由1端转换到2端，如图1(b)所示，试求t≥0 的电容电压uC(t)，并画出波形．

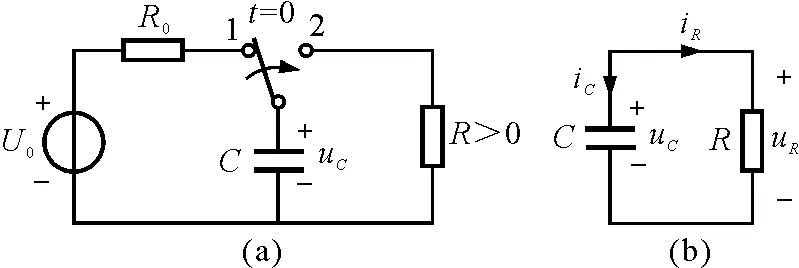
图1

解析：由图1(b)所示电路的KVL方程、KCL方程和VCR方程得到以下微分方程

上式是常系数线性一阶齐次微分方程，编写如下的Matlab程序来求该微分方程的解，并画出电压响应曲线．

clear all;clc

syms u t

uc=dsolve(′0.05*Du+u=0′,′u(0)=3.5′,′t′); %解微分方程(设时间常数RC=0.05 s，初始值3.5 V)

picture=ezplot(uc); set(picture,′color′,′k′,′LineWidth′,2) %画出时间常数RC=0.05 s时的波形

axis([0 0.30 3.5])

hold on

uc=dsolve(′0.02*Du+u=0′,′u(0)=3.5′,′t′); %解微分方程(设时间常数RC=0.02 s，初始值

3.5 V)

picture=ezplot(uc); set(picture,′color′,′k′,′LineStyle′,′--′,′LineWidth′,2) %画出时间常数RC=0.02s时的波形

axis([0 0.30 3.5])

xlabel(′t /s′,′FontSize′,14,′FontAngle′,′italic′);

ylabel(′u_c(t)/ V′,′FontSize′,14,′FontAngle′,′italic′)

legend(′RC=0.05s′,′RC=0.02 s′)

图2形象直观地展示了电容电压与电路时间常数之间的关系．电路时间常数RC的大小决定着电容电压放电的快慢，在课堂上容易修改RC的值，可绘制不同的曲线，帮助学生更好地了解RC零输入响应的特性．

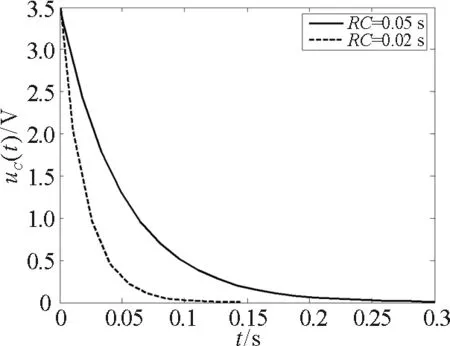
图2 RC电路零输入响应的波形

【例2】电路如图3所示, 试求RLC串联电路的响应，并画出响应波形．

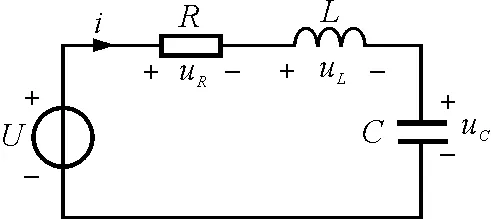
图3

解析：根据KCL，KVL和VCR方程，列出图3的微分方程

以上是二阶非齐次微分方程，用传统的笔算方法解此微分方程，对于大多数藏族学生来说有很大的难度，它是二阶电路分析教学中的难点．用Matlab强大的数值计算功能，很轻松地解出上面二阶微分方程，使师生们从繁重的数学计算中解脱出来，并顺利地完成该章节的学习任务．

使用ode45函数解此微分方程，先要把该二阶微分方程改写为一阶常微分方程组

然后，创建一个M函数文件myfun()，Matlab的代码设置如下：

function myfun()

clear all;clc

ts=[0,3];%

u0=[3;0.28];

[t,u]=ode45(@myfun1,ts,u0,[],6,1,0.04,0); %解微分方程，设参数值

picture=plot(t,u(:,1),′k′,t,u(:,2),′k--′); %画图

set(picture,′LineWidth′,2)

xlabel(′t′,′FontSize′,12,′FontAngle′,′italic′)

ylabel(′u_c(t) / i_L(t)′,′FontSize′,12,′FontAngle′,′italic′)

legend(′电压波形′,′电流波形′)

function up=myfun1(t,u,R,L,C,U)

up=[u(2);-(R/L)*u(2)-1/(L*C)*u(1)+U/(L*C)];

hold on

alpha=R/2*L;

text(1,2,[′衰减系数 alpha=′,num2str(alpha)])

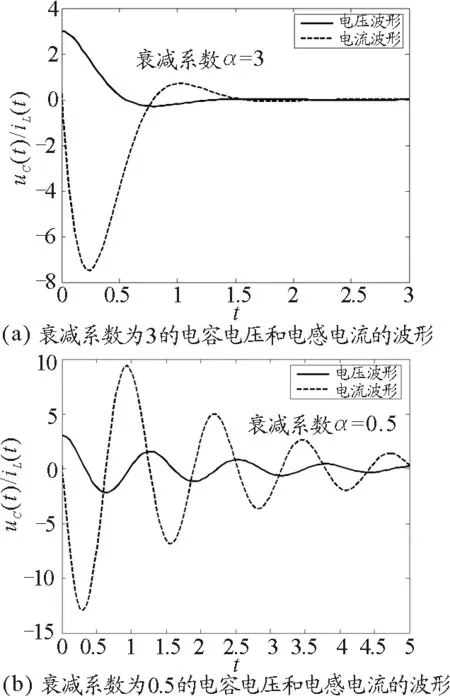
图4

图4(a)是电容电压初始值为3 V，电感电流初始值为0.28 A，R=6 Ω，L=1 H，C=0.04 F,U=0时得到的电容电压和电感电流的波形图；图4(b)是其他参数值不变，R=1时得到的图．另外，当U等于某常量时又可以得到直流激励下RLC串联电路的响应，因此该程序基本上通用于RLC串联的二阶电路分析．

2 利用Matlab求解RC电路的正弦稳态响应

【例3】图5所示的RC电路，电路原来已经达到稳定状态，在t=0时开关断开，正弦电流iS(t)=ISmcos(ωt+φi)作用于RC电路，求电容电压uc(t)的响应，并画图．

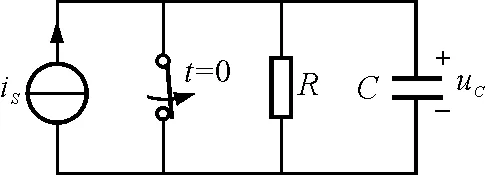
图5

解析：写出开关断开之后电路的微分方程

求解上述微分方程中，涉及到解三角函数方程，求解过程相当的繁琐，又容易出错，课堂上一直把解三角函数的过程跳过，直接给出结果．我们利用Matlab强大的数值计算的功能，解出上述正弦稳态响应的表达式，并把结果图形显示，Matlab的程序如下：

clear all; clc

syms u C R t w b I U

u=dsolve(′C*Du+1/R*u=I*cos(w*t+b)′,′u(0)=U′);

w=2;U=0;I=2;R=1;C=2;

b=pi/6; %theta

uc=eval(u); %电容电压的表达式

t=0∶0.001∶10;

uc3=eval(u); %电容电压的表达式

plot(t,uc3,′k′,′Linewidth′,2)

hold on

t=0∶0.001∶10;

uc1=-3226857735129493/9570149208162304*

exp(-1/2*t); %从上面的uc表达式中截取瞬态的响应

plot(t,uc1,′k--′,′Linewidth′,1.5)

hold on

t=0∶0.001∶10;

uc2=2/17*cos(2*t+1/6*pi)+8/17*sin(2*t+1/6*pi);%从上面的uc表达式中截取正弦稳态响应

plot(t,uc2,′k-.′,′Linewidth′,1.5)

grid on

xlabel(′t′,′FontSize′,12,′FontAngle′,′italic′)

ylabel(′u_c(t)′,′FontSize′,12,′FontAngle′,′italic′)

set(gca,′XTick′,[0 5 10]);

set(gca,′YTick′,[-0.4 -0.2 0 0.2 0.4]);

axis([0 10 -0.62 0.8])

legend(′电容电压的曲线′,′瞬态响应′,′正弦稳态响应′);

图6中实线波形是正弦稳态响应曲线，从整个时间段里看，该曲线并非按正弦规律变换，所以也就谈不上什么正弦稳态响应了．从图上看出，时间大概过了5 s之后，该曲线基本上正弦规曲线，那么5 s之前的曲线为什么不是正弦曲线呢？

为了解释这个现象，我们首先分析了由Matlab计算得到的电容电压的表达式，发现该表达式是由两个部分构成，我们把这两部分分别从表达式中截取后编程，其结果展示在一张图上(图6中的两个虚线波形)，通过上面技术上的处理后我们清楚地看到，实线的波形是两个虚线波形的叠加，即一个按正弦规律变化的曲线(稳态)，另一个按指数规律递减的曲线(瞬态)，当瞬态响应消失之后(理论上消失它需要无限长时间，实际上瞬态响应在极短的时间里消失完)，剩下的只是稳态响应，我们所说的正弦稳态响应就是这剩下的响应．如果不借助计算机的可视化功能，上面的现象在课堂上很难用语言来解释清楚．

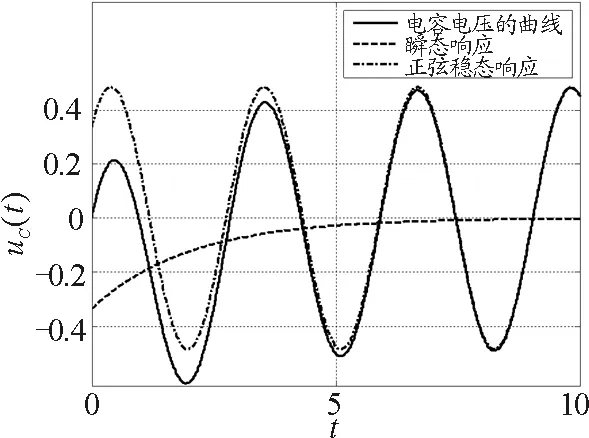
图6 正弦稳态响应

3 利用Matlab研究RLC谐振电路的频率特性

【例4】图7所示电路为RLC串联谐振电路，画出该谐振电路的频率特性曲线．

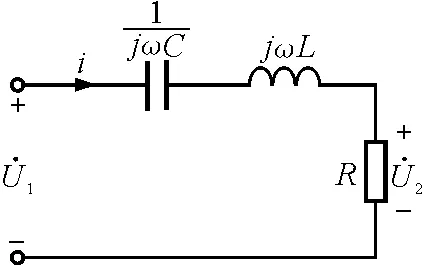
图7

解析：图7所示电路的转移电压比为

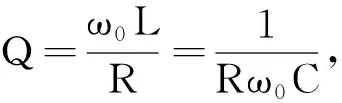
根据以上表达式，编写Matlab程序如下：

%求网络函数的幅值，画幅频特性曲线

clear all;clc; figure(1)

w0=500; Q=[0.5 1 2];

w=1∶500000;

for i=1∶3

H=abs(1./(1+j*Q(i)*(w/w0-w0./w)));

if i==1

semilogx(w/w0,H,′k--′,′Linewidth′,2)

end

if i==2

semilogx(w/w0,H,′k′,′Linewidth′,2)

end

if i==3

semilogx(w/w0,H,′k:′,′Linewidth′,2)

end

xlabel(′omega/omega_c′)

ylabel(′|H(jomega)|′)

set(gca,′XTick′,[0.001 0.01 0.1 1 10 100 1000]);

set(gca,′YTick′,[0 0.5 0.707 1 ]);

axis([0 1000 0 1.05])

hold on

end

legend(′Q=0.5′,′Q=1′,′Q=2′);

%求网络函数的相位角，画出相频特性

clear all;clc; figure(2) %lun7

w0=500;Q=[0.5 1 2];w=1∶500000;

for i=1∶3

Theta=angle(1./(1+j*Q(i)*(w/w0-w0./w)));%计算复数角度(弧度)

Theta=Theta*180/pi;%弧度变成角度

switch i

case 1

semilogx(w/w0,Theta,′k--′,′Linewidth′,2)

case 2

semilogx(w/w0,Theta,′k′,′Linewidth′,2)

case 3

semilogx(w/w0,Theta,′k:′,′Linewidth′,2)

end

xlabel(′omega/omega_c′)

ylabel(′ heta(omega)′)

set(gca,′XTick′,[0.01 0.1 1 10 100 1000 ]);

set(gca,′YTick′,[-90 0 90]);

axis([0 1000 -90 90])

hold on

end

legend(′Q=0.5′,′Q=1′,′Q=2′);

根据电路分析的理论知道，频带宽度与品质因数Q成反比，Q越大，带宽越窄，曲线越尖锐，对信号的选择性越好，Matlab可视化得到的图8(a)能生动形象地展示这个现象．图8(b)是相频特性曲线，它表明电压U1和U2之间的相位关系．

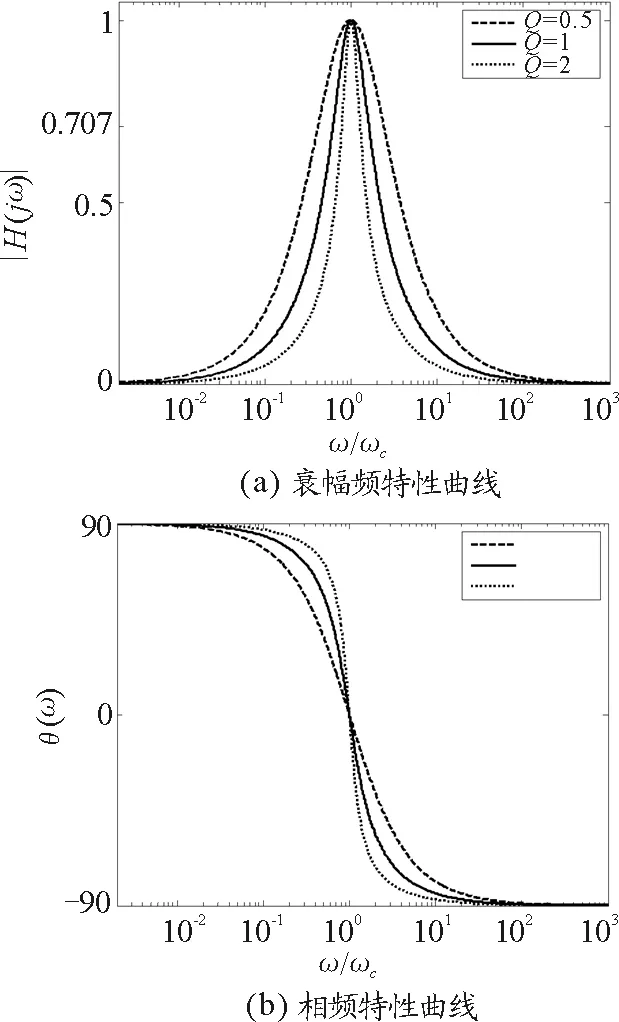
图8

4 总结

由于Matlab软件有诸多突出的优点，大部分高等院校已经把它列入课程计划中，成为学生必须掌握的基本软件之一．由于在电路分析中涉及大量的数学运算问题，并且往往需要其抽象的计算结果用图形来展示，而Matlab恰好具有这个功能，因此我们尝试着把它引入到电路分析的教学中，经过几年的教学实践表明，这种计算机辅助教学方式是可行的，取得了较显著的教学效果，深受学生的喜爱，认为计算机辅助教学方式可以在其他课程教学中去尝试和推广．

致谢：目前，西藏大学应用物理专业和电子信息工程专业使用的电路分析课程教材是由胡翔骏编著的《电路分析》(第2版)，因此文章中的实例均从该教材中改编而来，在此对该书作者表示感谢；同时也感谢匿名评审专家为本文提出的有益问题．

参考文献

1 胡翔骏. 电路分析(第2版).北京: 高等教育出版,2007

2 曹戈.Matlab 教程及实训. 北京: 机械工业出版社,2008

3 Desmond J.Higham,Nicholas J.Higham.MATLAB guide-2nded.USA:Societyfor Indus-trial and Applied Maathematics,2005

4 求是科技.Matlab7.0从入门到精通.北京:人民邮电出版社,2006