存在空气阻力情况下的平抛运动轨迹研究

狄 龙 张启迪

(淮北市第一中学 安徽 淮北 235000)

1 问题的提出

平抛运动在高中物理教学过程中是一个常见内容，在高中物理新课程标准教科书中是这样定义抛体运动和平抛运动的：以一定的速度将物体抛出，如果物体只受到重力的作用，这时的运动叫做抛体运动(Projectile Motion)．可以看出，教科书中的定义忽略了实际存在的空气阻力．很多情况下，我们可以用这种理想模型去研究初速度水平的抛体运动，但是，若考虑存在空气阻力情况下，运动的情形到底是如何的呢？

现在我们就来研究当空气阻力满足f=-kv时，初速度水平的抛体运动的轨迹情况．

2 理论推导

2.1 抛物体动力学方程

首先对小球进行受力分析，小球受到重力mg，方向竖直向下；空气阻力f=-kv，方向与速度方向相反，根据牛顿第二定律可以列方程

(1)

又由于

上式可化为

分离变量可得

积分得

2.2 抛物体运动变化规律

2.2.1 速度随时间的变化规律

当t=0时，vx=v0,vy=0,可得

Cx=-v0Cy=-g

因此得速度随时间变化规律

(2)

2.2.2 位置随时间变化规律

当t=0时，x=0,y=0，积分上式可得位置随时间变化规律

(3)

这也是小球以t为参数的轨迹方程．

2.2.3 平抛运动的长期行为

当t→∞时，由上式可得

(4)

所以在有阻力的情况下，长期来看，水平方向的速度为零，而竖直方向的速度是趋于一个常数，这个常数和物体所受重力和阻力系数有关．位移为

(5)

可见，长期看来，平抛小球在考虑空气阻力的情况下，水平方向有一个极限位移，在竖直方向上是做匀速直线运动的．

2.2.4 阻力可忽略时的情况

当k→0时，可得

这也就是我们在中学物理课程中忽略空气阻力处理此问题时，所得到的结论．对于水平和竖直方向的位移，由上边的式子可得

即

(5)

3 软件模拟并与理论推导对比

笔者同时运用Matlab软件对此过程进行了模拟．所得到的横坐标、纵坐标随时间变化的规律如图

1(a)所示，平抛运动轨迹图如图1(b)所示．

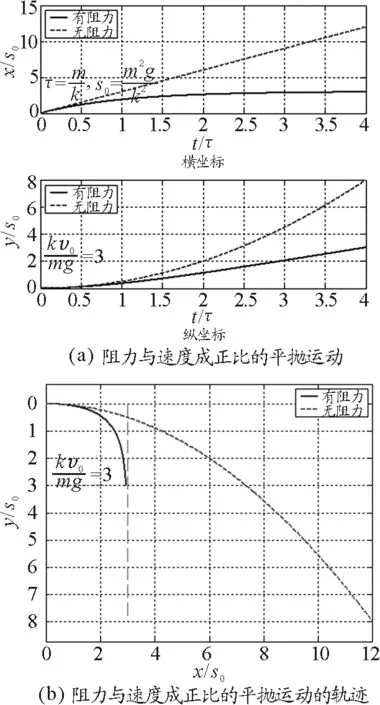
图1

(1)图1(a)中上图的横坐标表示运动时间，纵坐标表示水平方向上位移的大小，图1(b)下图横坐标表示运动时间，纵坐标表示竖直方向位移的大小；图1(b)中横坐标表示水平方向位移大小，纵坐标表示竖直方向上位移大小．

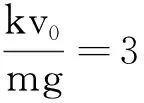
从以上图像我们可以看出，相比于没有阻力的情况下，小球的横纵坐标都要小一些．在没有阻力的情况下，小球的运动轨迹是抛物线，而在有阻力的情况下，小球的运动轨迹是一条弯曲的曲线，且弯曲程度要比无阻力情况下明显．在有阻力的情况下，水平方向有一个极限距离，而竖直方向趋向于匀速直线运动．通过这三幅图，就可以清楚地展示出平抛运动在考虑空气阻力时的运动性质，与前面的数学推导也是一致的．