剪力钉集束式与均布式布置下钢-混 组合梁桥受力分析
2014-06-27刘沐宇
刘沐宇, 万 杰, 张 强
(1.武汉理工大学 道路桥梁与结构工程湖北省重点实验室,湖北 武汉 430070;2.中铁大桥勘测设计院集团有限公司,湖北 武汉 430050)
钢-混组合梁桥是通过剪力钉连接混凝土桥面板与钢主梁,以保证二者共同作用。目前,剪力钉布置方式主要采用均布式,其剪力钉受力具有比较均匀的特征,但是也造成混凝土桥面板分块和湿接缝较多,引起施工不便和增加工期。港珠澳大桥钢-混组合连续箱梁的剪力钉采用了新颖的集束式布置方式,它可以对桥面板进行分块预制整体拼装,具有施工速度快、安装质量好、钢-混组合梁整体性能优越的特点。但是,剪力钉集束式布置对钢-混组合梁桥整体受力性能的影响和剪力钉的受力性能成为桥梁设计人员非常关心的问题。据此,开展剪力钉集束式和均布式布置下钢-混组合梁桥受力特性分析研究,对掌握钢-混组合梁桥的设计方法和营运性能具有重要的理论意义。
目前国内外学者对大跨径钢-混组合梁桥结构性能开展了相关的研究。周伟翔[1]等对上海长江大桥组合箱梁建立有限元模型进行全桥仿真分析,并用弹簧单元模拟剪力钉。分析最不利荷载下组合梁边跨的受力性能,并对剪力钉的承载力进行了验算和复核;苏庆田等[2,3]以上海长江大桥为工程背景,采用通用有限元ANSYS程序对索塔建立空间模型,采用弹簧单元模拟剪力钉,分析了索塔内剪力钉在斜拉索索力作用下的力学性能。王正阳等[4]以某槽型钢-混组合梁斜拉桥为研究对象,采用弹簧单元模拟剪力钉,建立全桥空间有限元模型,分析了剪力钉纵、横桥向受剪性能。
由上可知,剪力钉的模拟方法主要采用弹簧单元来实现,然而弹簧单元存在以下问题。
(1)弹簧单元的刚度k取值主要来自推出试验的结果,而剪力钉在推出试验条件下的受力状况与钢-混组合梁桥剪力钉的受力状况是存在差异的。
(2)弹簧单元只能提取剪力钉单向受力情况,而不能提取剪力钉的应力情况。因此,用弹簧单元模拟剪力钉会由于刚度k的取值不同而产生较大的误差。采用梁单元模拟剪力钉,由于输入参数为剪力钉的弹性模量E、泊松比μ、截面面积A、以及长度L,它取值精准,克服了上述不足。
本文针对港珠澳大桥非通航孔6×85 m组合连续梁桥开展受力性能分析,采用Beam188梁单元模拟剪力钉、Solid45实体单元模拟混凝土桥面板、Shell163壳单元模拟钢箱梁,在最不利边跨建立了精细的空间有限元模型(按剪力钉实际数量建立梁单元),采用生死单元法模拟港珠澳大桥的实际施工过程,即大节段整体吊装、简支变连续、支点顶升与回落、支点纵向预应力张拉以及二期恒载的全过程。按照剪力钉集束式布置和剪力钉均布式布置两种方式,分别计算了钢-混组合梁桥受力性能和剪力钉的受力状况,为钢-混组合梁桥剪力钉集束式布置提供分析依据。
1 工程概况
港珠澳大桥浅水区非通航孔桥分幅方案采用6×85m连续组合钢箱梁,如图1所示。桥面总宽33.1 m,两幅主梁中心距16.8 m,单幅桥面宽16.3 m,桥面横坡2.5%,如图2所示。

图1 6×85 m连续组合梁桥跨总布置图/cm

图2 连续组合梁截面/mm
大桥主要技术标准如下。
(1)公路等级:主桥采用双向八车道。
(2)设计荷载:公路I级。
(3)设计寿命:120年。
(4)设计安全等级:一级。
(5)环境类别:I类。
2 建立钢-混组合梁桥有限元模型
本文以港珠澳大桥6×85 m钢-混组合连续梁桥为分析对象,采用全桥简化模型单跨精细模型,即Ansys子模型技术。剪力钉集束式和均匀式单跨精细子模型选取全桥模型中剪力钉受力最不利的85 m边跨,采用生死单元法模拟港珠澳大桥的实际施工过程,即大节段整体吊装、简支变连续、支点顶升与回落、支点纵向预应力张拉以及二期恒载的全过程,以全桥简化模型切割边界上的位移作为精细模型的边界条件。
钢-混组合梁桥精细有限元模型采用Beam188梁单元模拟剪力钉、Solid45实体单元模拟混凝土桥面板、Shell163壳单元模拟钢箱梁。剪力钉集束式空间精细有限元模型共包含单元84666个,节点90856个;剪力钉均布式空间精细有限元模型共包含单元90156个,节点98232个,有限元模型如图3和图4所示。

图3 剪力钉集束式精细有限元模型

图4 剪力钉均布式精细有限元模型
港珠澳组合连续梁材料参数见表1。

表1 有限元分析主要材料参数
3 组合梁计算结果及分析
分析组合梁空间受力状态考虑的荷载工况如下:
(1)成桥阶段恒载工况;
(2)最不利活载工况;
(3)荷载组合工况:成桥阶段恒载+活载。
3.1 成桥阶段恒载工况
由图5与图6可知,成桥阶段恒载工况下剪力钉集束式与均布式跨中最大挠度分别为202.5 mm和202.7 mm。

图5 剪力钉集束式位移
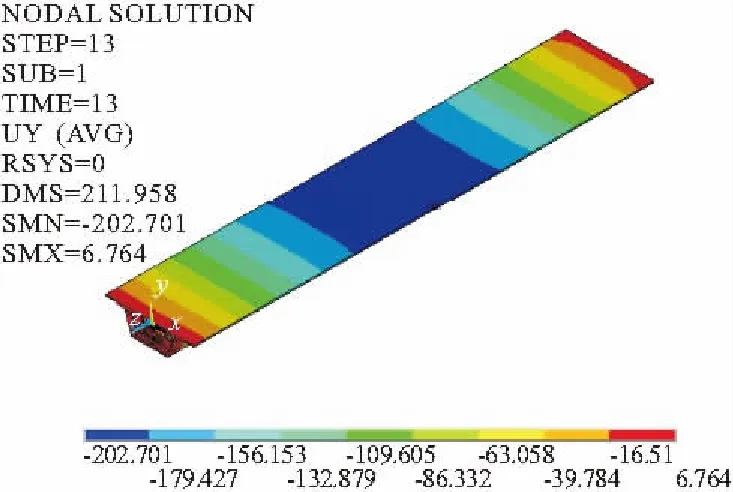
图6 剪力钉均布式位移

图7 剪力钉集束式跨中混凝土桥面板应力
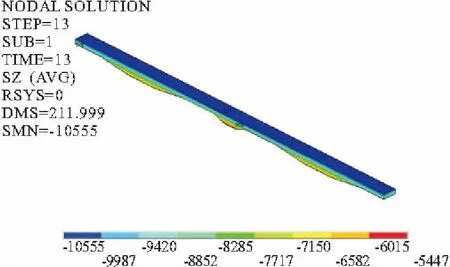
图8 剪力钉均布式跨中混凝土桥面板应力
由图7与图8可知,成桥阶段恒载工况下两种剪力钉布置形式跨中混凝土桥面板最大应力都位于桥面板顶面,集束式最大应力为-10.7 MPa,均布式最大应力为-10.5 MPa。
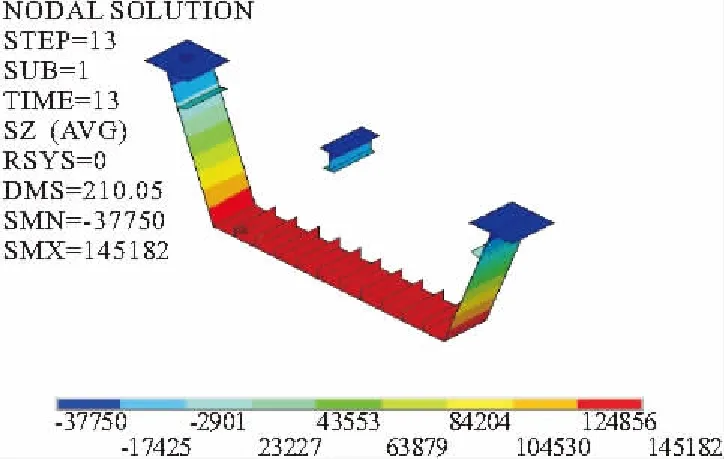
图9 剪力钉集束式跨中钢梁应力
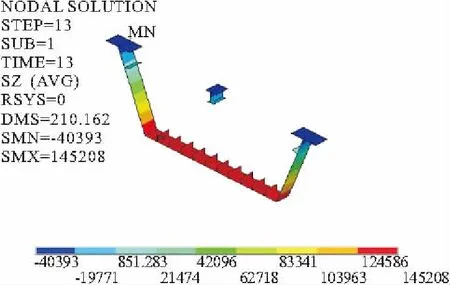
图10 剪力钉均布式跨中钢梁应力
由图9与图10可知,成桥阶段恒载工况下两种剪力钉布置形式跨中钢梁最大拉应力都位于钢梁底板,集束式最大应力为145.4 MPa,均布式最大应力为145.2 MPa;跨中钢梁最大压应力都位于钢梁顶板,集束式最大应力为-37.8 MPa,均布式最大应力为-37.4 MPa。
3.2 最不利活载工况和组合工况
剪力钉集束式与均布式在最不利活载工况与组合工况下,组合梁边跨跨中最大挠度、混凝土桥面板最大应力、钢梁最大拉应力和最大压应力分别列于表2和表3中。

表2 最不利活载工况边跨跨中组合梁受力特性
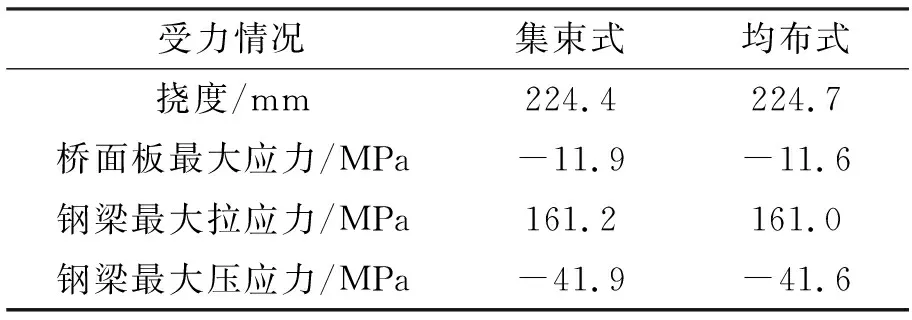
表3 组合工况边跨跨中组合梁受力特性
4 剪力钉计算结果及分析
分析剪力钉受力状态考虑的荷载工况:
(1)成桥阶段恒载工况;
(2)最不利活载工况;
(3)荷载组合工况:成桥阶段恒载+活载。
考虑结构横向对称,仅取边跨85 m梁一侧的剪力钉进行结果分析。结果坐标系以纵梁顶板与腹板交点作为原点,纵向为x轴,横向为y轴。且考虑到剪力钉数目纵多,因此每个工况下剪力钉的受力仅取最大值所在列的结果列于图表中。
4.1 纵向剪力计算结果分析
(1)成桥阶段恒载工况
图11为成桥阶段恒载工况下,两种布置形式剪力钉纵向剪力最大值所在列的剪力分布图,都为靠近腹板所在列,可见靠近腹板的剪力钉承担了比远离腹板的剪力钉更多的剪力。由此可见,恒载工况下均布式剪力钉纵向剪力比集束式纵向剪力分布连续均匀。由于港珠澳大桥采用整体吊装、支点顶升及回落和负弯矩区桥面板张拉预应力等施工工艺,两种布置形式的剪力钉都在新老混凝土交界处纵向剪力较大,最大值出现在x=63.4 m处,其中集束式剪力钉最大纵向剪力为57.54 kN,均布式为60.87 kN。

图11 成桥阶段恒载工况剪力钉纵向剪力分布
(2)最不利活载工况
根据成桥阶段恒载工况下剪力钉纵向受力最不利位置,选取x=63.4 m按照该截面建立影响线进行最大纵向剪力加载。
由图12可见,最不利活载工况下均布式剪力钉纵向剪力比集束式剪力钉纵向剪力分布连续均匀。在x=63.4 m处集束式剪力钉最大纵向剪力为6.95 kN,均布式为7.11 kN。
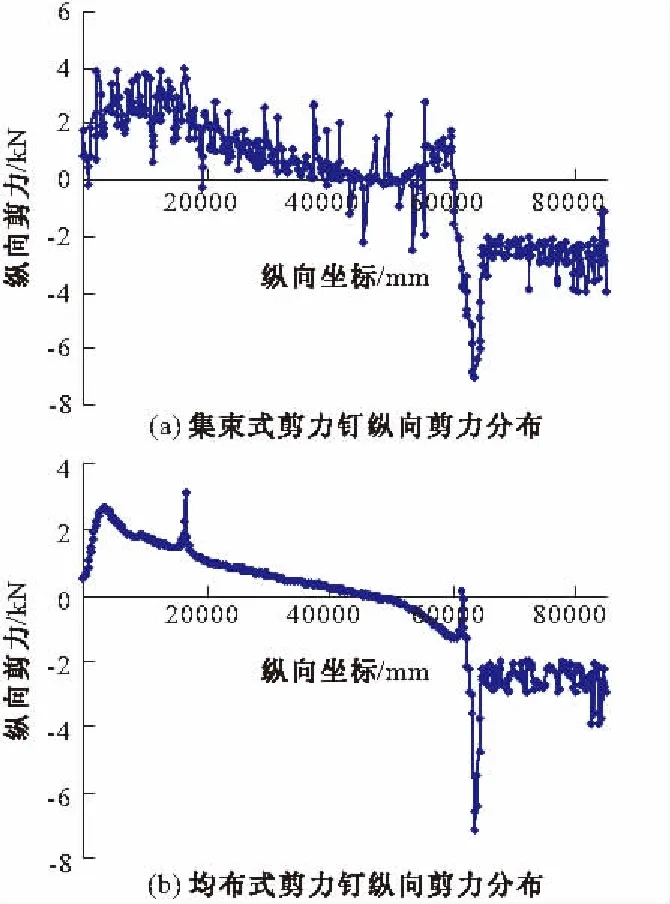
图12 最不利活载工况剪力钉纵向剪力分布
(3)荷载组合工况
由图13可见荷载组合工况下两种布置形式剪力钉在x=63.4 m纵向剪力最大,其中集束式剪力钉最大纵向剪力为64.49 kN,均布式为67.98 kN,比集束式大3.49 kN。

图13 荷载组合工况剪力钉纵向剪力分布
4.2 拉拔力计算结果分析
(1)成桥阶段恒载工况
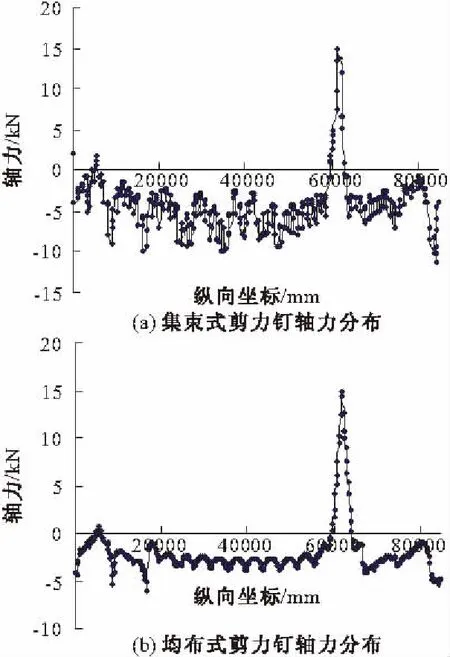
图14 成桥阶段恒载工况剪力钉轴力分布
图14为成桥阶段恒载工况下两种布置形式剪力钉拉拔力最大值所在列的轴力分布图。由图可见,两种布置形式剪力钉轴力都以受压为主,但由于施工过程的影响,两种布置形式剪力钉在x=61.4 m附近产生部分拉拔力,其中集束式剪力钉最大拉拔力为14.9 kN,均布式为14.83 kN。
(2)最不利活载工况
根据组合梁拉拔力产生机理,在x=61.4 m处对组合梁边跨进行最不利加载,如图15所示。
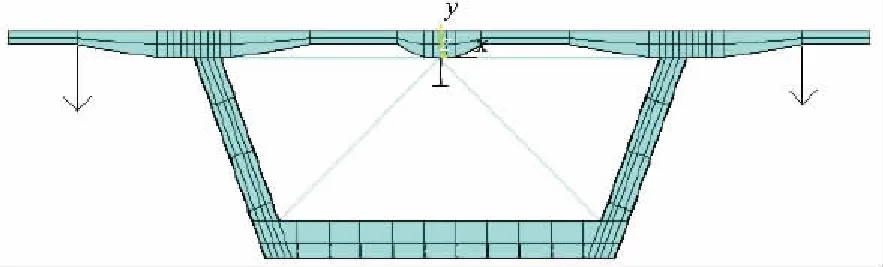
图15 有限元模型悬臂端偏载示意

图16 最不利活载工况剪力钉轴力分布
由图16可见,最不利活载工况下两种布置形式剪力钉产生的最大拉拔力都发生在腹板横向加劲肋附近最内侧一列剪力钉,其中集束式剪力钉最大拉拔力为30.45 kN,均布式为28.84 kN。
(3)荷载组合工况
由图17可见荷载组合工况下,两种布置形式剪力钉在x=61.4 m拉拔力最大,其中集束式剪力钉最大拉拔力为45.44 kN,均布式为43.67 kN,比集束式小1.77 kN。
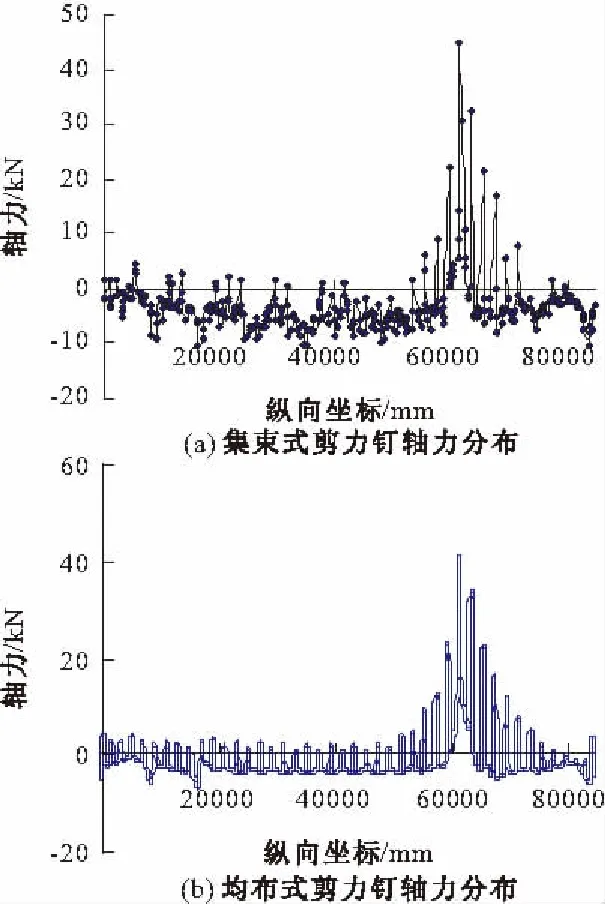
图17 荷载组合工况剪力钉轴力分布
5 结 论
(1)钢-混组合梁采用梁单元模拟剪力钉可以有效避免弹簧单元的不足,使计算结果更加精确,为模拟剪力钉提供一种新途径。
(2)钢-混组合连续梁桥施工过程直接影响剪力钉受力情况,因此对剪力钉模拟过程中应依照组合连续梁全桥实际施工过程进行建模,并且采用Ansys子模型技术能够考虑全桥施工过程对最不利边跨剪力钉受力的影响。
(3)有限元分析得到组合荷载工况下剪力钉集束式与均布式组合梁跨中最大挠度分别为224.4 mm和224.7 mm,混凝土桥面板最大应力分别为-11.9 MPa和-11.6 MPa,钢梁最大应力分别为161.2 MPa和161.0 MPa,比较发现两种剪力钉布置形式组合梁受力基本相同。组合荷载工况下剪力钉集束式与均布式布置最大纵向剪力分别为64.49 kN和67.98 kN,最大拉拔力分别为45.44 kN和43.67 kN,可以得到两种布置形式剪力钉受力都满足正常使用要求,而且差异较小。
(4)考虑到剪力钉集束式布置可以对桥面板进行分块预制整体拼装,因此港珠澳大桥钢-混组合连续梁桥剪力钉选择集束布置更为合理。
[1] 周伟祥. 连续组合梁桥钢与混凝土连续连接试验研究[D]. 上海:同济大学,2007.
[2] 苏庆田,刘玉擎,曾明根. 钢-混组合箱梁桥受力的有限元仿真分析[J]. 桥梁建设,2006,36(7):916-921.
[3] 苏庆田.苏通大桥索塔栓钉剪力连接件的力学性能试验[J].同济大学学报(自然科学版),2008,(5):28-31.
[4] 王正阳,吴 冲. 斜拉桥钢-混组合箱梁焊钉连接件剪力分布研究[J]. 中国水运,2010,10(1):150-152.
[5] 唐 琎,叶梅新. 钢-混凝土组合结构中密集型剪力钉群的受力状态[J].长沙铁道学院学报,1999,17(4):68-73.
[6] 罗如登,叶梅新. 组合梁与混凝土板相对滑移及栓钉受力状态研究[J]. 铁道学报,2002,24(3):57-61.
[7] 许 伟,王 坤. 钢与高强混凝土连续组合梁连接件的布置方式[J]. 东北大学学报(自然科学版),2005,26(9):901-904.
[8] 候文岐,叶梅新. 铁路桥梁群钉组合结构极限承载力和静力行为分析[J]. 中国铁道科学,2011,32(1):55-61.
[9] Hawkins N M. Seismic response of composite shear connections[J]. Journal of Structural Engineering,1984,110(9):2120-2136.
[10] 刘沐宇,王 松. 港珠澳大桥组合连续箱梁桥剪力钉受力分析[J]. 武汉理工大学学报,2013,35(2):118-123.
