自复位摩擦耗能支撑框架的抗震性能分析

胡 丹, 周 臻, 苗建义, 王维影

(1.中广电广播电影电视设计研究院，北京 100045; 2.东南大学 土木工程学院，江苏 南京 210096)

自复位抗震结构体系由于能够有效减小结构残余变形，控制结构损伤的发展，降低结构的震后修复成本，成为现代结构抗震损伤控制设计的研究热点和发展趋势。目前，自复位结构主要包括三种形式：(1) 后张预应力梁柱节点[1]：允许梁柱节点在地震作用过程中张开和闭合，通过水平预应力使结构复位；(2) 摇摆体系[2]：允许结构竖向承重构件在基础连接处发生上翘摇摆，通过自重或竖向预应力使结构复位；(3) 自复位支撑[3]：支撑不仅承担耗能减震作用，同时提供自复位力使结构复位。前两种自复位结构体系都需要改变主体结构原有的节点连接方式或竖向承重体系，而自复位支撑则只需替换结构原有支撑构件，而不必对主体结构体系做任何变动就可使结构具有自复位能力，因而相对其他自定心体系具有天然优势，无论对新建结构设计还是既有结构加固都具有重要意义，近年来日益受到重视。

Christopoulos[3]等将由芳纶纤维后张预应力筋与内外套管构成的自复位体系引入支撑中，并与摩擦型耗能元件结合，形成了自复位摩擦型耗能支撑(Self-centering Friction Energy Dissipative Braces, SCFED)，并通过支撑构件试验验证了其良好的耗能能力与自复位能力。本文将SCFED应用于一9层抗弯钢框架Benchmark模型，采用OpenSEES有限元软件进行非线性静力推覆分析(Pushover)和非线性动力时程分析，通过与另一种常用耗能支撑-屈曲约束支撑[4](Buckling Restrained Braces, BRB)的比较，深入研究SCFED对框架结构抗震性能的影响，为这一新型支撑在框架结构工程中的应用提供依据。

1 SCFED的受力特征

自复位摩擦型耗能支撑的工作机理如图1所示：内外套管与预应力筋和端板一起构成了自复位体系，预先张拉的预应力筋将两侧端板紧紧顶在内外管两端。内外管还分别焊有摩擦板，随着内外套管的相对滑动进行摩擦耗能。当外力克服了摩擦力和初始预应力，内外套管便开始相对滑动，无论支撑受拉或受压，预应力筋始终处于拉伸状态，从而提供自复位能力。

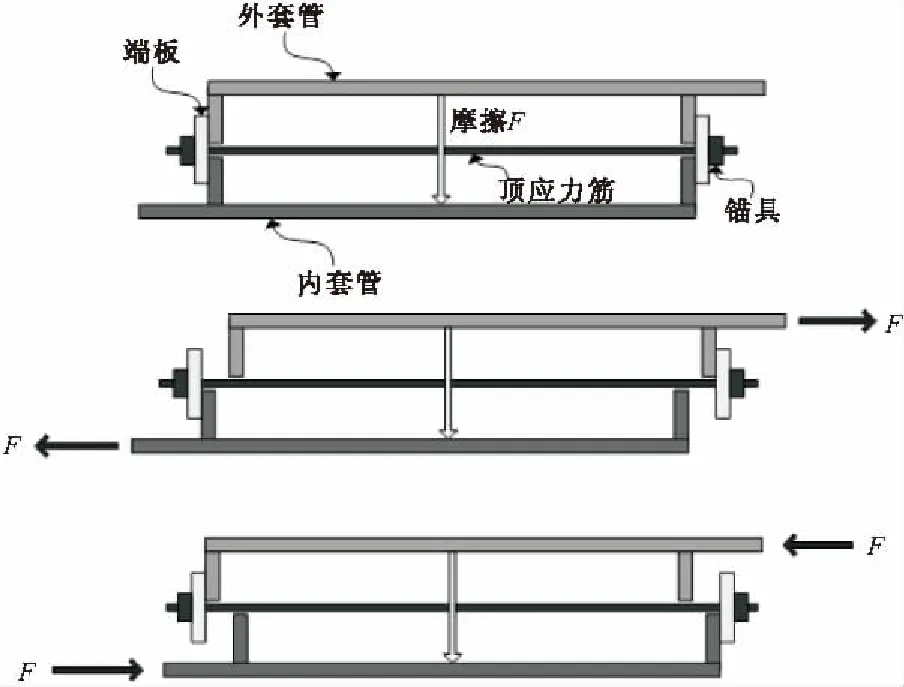
图1 SCFED的工作原理

图2给出了典型SCFED的滞回特性曲线，其中，k1表示支撑的第一刚度，由内外套筒刚度和预应筋叠加而成；k2表示支撑第二刚度，为预应力筋的刚度；Fp表示支撑的启动力，由预应力筋中的预应力与摩擦板的摩擦力叠加而成；β表示加载阶段和卸载阶段启动力的比值。由图2可知，SCFED的滞回曲线具有明显的旗帜型特征，无论是受拉还是受压，支撑在预应力筋中自复位力的作用下，均能回到初始位置，从而能够有效克服传统支撑的残余变形，进而控制主体结构的残余变形。

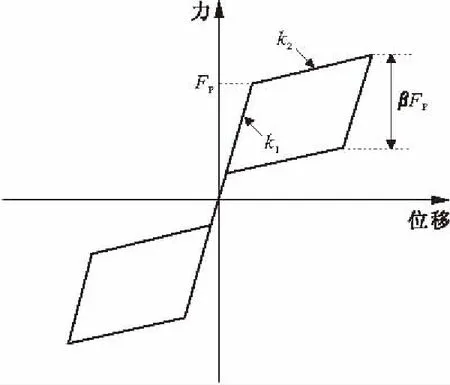
图2 典型SCFED滞回曲线

2 框架的有限元模型

本文选取美国土木工程学会(ASCE) Benchmark问题第三阶段研究的模型结构-9层钢框架作为研究对象[5]，如图3所示：该结构有一层地下室，一层层高5.49 m，其余各层层高均为3.96 m；柱和地面基础固接，地下室柱和底板铰接，柱的两层留有一个接头，接头和下层楼板的距离为1.83 m；钢材为双线型随动强化模型，弹性模量为2.06×105MPa，强化系数为3%；梁、柱屈服强度分别为248 MPa和345 MPa，不考虑强度和刚度的退化。楼层质量和梁、柱截面尺寸如图中所示，模型中每一层的地震质量以集中质量形式施加在梁柱节点上。在原有框架结构的基础上，采用中心支撑的布置方式，支撑与框架之间采用铰接连接。

图3 9层Benchmark钢框架

采用OpenSEES有限元软件建立Benchmark支撑框架的分析模型。支撑考虑分别采用屈曲约束耗能支撑(BRB)和自复位摩擦型耗能支撑(SCED)两种类型，从而建立BRB框架和SCED框架有限元模型，对比其抗震性能分析结果。梁、柱单元采用Nonlinear Beam-column Element来模拟，本构关系模型采用Steel01 Material。BRB采用Truss单元模拟，本构关系模型为Steel02 Material，屈服强度取为290MPa，弹性模量为2.06×105MPa，强化系数为1%。研究表明，BRB与支撑框架结构的刚度比宜取2～3[6]，本文取为2.5，由此可确定各层单根BRB的截面面积如表1所示。

SCFED采用OpenSEES中的Self-centering material模拟。预应力筋假定为芳纶纤维筋，弹性模量取为102 GPa。其设计按照与BRB等强度原则进行替换，即SCFED的启动力等于BRB的屈服力，并取β为0.9，从而得到相应的预应力与摩擦力。然后依据每根预应力筋的预应力与其弹性极限应力的比值为0.3，可确定出每根SCFED的预应力筋面积，从而可确定SCFED的第二刚度。然后按照文献[3]中的构造设计方法可确定内外管刚度，由此得到SCFED的参数如表2所示。其中内外套管均为正方形套管。

表1 框架各层每根BRB核心板尺寸和截面积

表2 SCFED的构造参数和力学性能参数

3 非线性静力推覆分析

对纯框架、BRB框架与SCFED框架均采用非线性静力推覆分析(Pushover)，加载形函数采用结构的第一阶模态，分析时考虑结构的P-Δ效应。根据分析结果可得BRB框架和SCFED框架中结构与支撑的刚度比分别为2.5和4.5，强度比均为1.5。图4给出了两种支撑框架结构的基底剪力-顶点位移角曲线，其中顶点位移角为顶点位移与框架总高度的比值。可以看到，BRB框架和SCFED框架屈服时的基底剪力较为接近，但BRB框架在屈服后的刚度退化更为明显，这有可能会导致主体结构薄弱层的出现，加剧结构的局部损伤，从而引起结构残余变形。

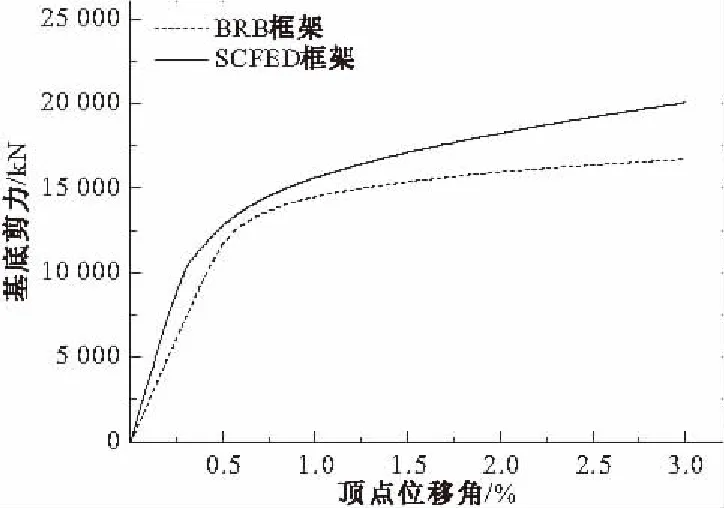
图4 基底剪力-顶点位移角关系

图5给出了两种支撑框架结构在顶点位移角分别为1%、2%和3%时，各楼层的位移角分布。由图可知，当结构位移较小时，BRB支撑大部分均处于弹性阶段，因此结构刚度退化不明显，整体变形与SCFED框架接近，且各层变形较为均匀。随着结构位移的增加，BRB框架中的各层支撑相继进入屈服，结构刚度逐渐退化，导致楼层间位移分布的不均匀性逐渐明显。而SCFED框架由于自复位体系提供的第二刚度，能够有效控制结构位移的不均匀性，尤其当结构位移较大时，其优势较BRB结构更为明显。

图5 两种框架的楼层位移角分布

4 非线性动力时程分析

综合考虑我国抗震设计规范的相关要求和ATC-63的地震动选取建议[7]，从美国太平洋地震工程研究中心(PEER)强震记录数据库中按以下原则选取10条地震记录：(1)地震震级≥6.5；(2)断层距大于10 km；(3)PGA≥0.2 g，PGV≥15 cm/s；(4)场地条件选取USGS分类中的C类、Geomatrix分类中的 D类和Taiwan CWB分类中的2类，与我国规范中的Ⅲ类场地接近；(5)同一地震只选1条记录。选取的地震波记录及其特征参数如表3所示。计算时将地震波记录均按照地面峰值加速度为620 cm/s2进行调幅，相当于我国规范的9度大震水平，采用非线性动力时程分析，分析时也考虑结构P-Δ效应。

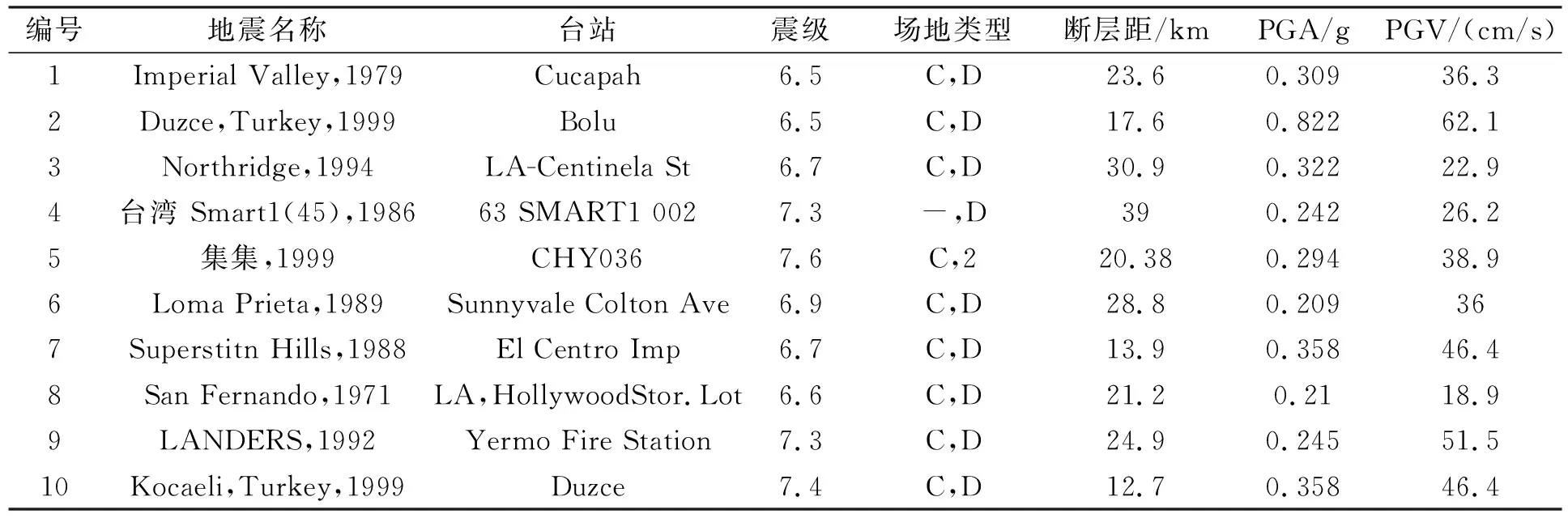
表3 选用的地震波记录

图6(a)为两种支撑框架结构在10条地震波作用下的非线性动力时程分析位移结果。由文献[3]可知，芳纶纤维的极限应变为2.3%，按支撑在框架中布置角度为30°计算，可得到保证支撑正常工作(即芳纶纤维筋不断裂)的最大层间位移角约为5%，由图6(a)可知两种框架的支撑均在正常变形范围内。在10条地震波作用下，SCFED框架的最大层间位移角均小于BRB框架，平均最大层间位移角分别为1.76%和1.26%，其均值减小约28.6%。这主要是因为SCFED框架结构在屈服后的刚度较BRB框架结构高，有利于减小结构在强地震作用下的峰值位移响应。在最大残余位移角方面，SCFED框架平均值为0.03%，显著低于BRB框架的0.47%，表明SCFED支撑中的自复位体系有效减小了结构的残余变形。有研究认为，当结构残余位移角达到0.5%～1.0%时，虽然可以安全进入但是已不适合居住[8]。由图6(a)中结果可知，BRB框架结构在编号分别为5、7、9、10的四条地震波作用下，其最大残余位移角均超过了0.5%，且在9号地震波作用下甚至达到了1.0%，而SCFED框架在各条地震波作用下的最大残余位移角均小于0.1%，可见SCFED框架在控制结构残余变形与增强结构震后可修复能力方面较BRB框架具有明显的优势。

(a)最大层间位移角与残余位移角 (b)各楼层位移角均值分布 (c) 损伤集中系数图6 两种支撑框架结构非线性动力时程分析的位移结果

图6(b)为各楼层最大位移角均值与残余位移角均值的分布结果。由图6(b)可知，SCFED框架和BRB框架在第5层以上的最大层间位移角均值较为接近，但在第5层以下则存在显著差异，第1～4层SCFED框架的位移角均值比BRB框架明显减小，其原因在于BRB框架结构在大震作用下进入屈服后，易在底部形成刚度较小的薄弱层，因此损伤容易集中于结构底部几层，导致层间位移角的显著增大。而SCFED中由于自复位体系的存在，能够有效抑制薄弱层的形成，因此层间位移角分布更为均匀。

图6(c)为各地震波激励下的结构损伤集中系数DCF分布，DCF的定义如下：

DCF=(Δ/hs)/(Δroof/hn)

(1)

式中：Δ和Δroof分别指最大层间位移和顶层位移；hs和hn分别指楼层高度和整个建筑的高度。DCF越大，表明结构损伤越集中，薄弱层效应越明显。由图6(c)可以看到，除第8条地震波两者较为接近外，其余9条地震波作用下SCFED框架的DCF均明显小于BRB框架，尤其第3条地震波作用下更为明显，表明SCFED框架能够有效减小结构的损伤集中现象，这也是其残余位移较小的主要原因。有研究表明[9]，BRB框架的平均残余层间位移角变形为最大层间位移角的40%～60%，但其结果是针对铰接框架得到的。而本文分析的框架为抗弯框架，其残余位移角应较铰接框架更小[10]。而根据本文10条地震波的分析结果(图6)，BRB框架结构的平均残余层间位移角为最大层间位移角的10%～20%，而SCFED框架的残余层间位移角则仅为最大层间位移角的1%～2%。

图7 第3条地震波作用下框架顶层支撑滞回曲线

图7为第3条地震波作用下框架结构顶层支撑的滞回曲线。由图7(a)可知，BRB在屈服后将会产生较大的塑性变形，当荷载消失后将会产生较大的残余变形；而SCFED虽然在地震过程中经历了较大的变形(图7(b))，但一旦地震作用消失，仍然能够回到初始位置，因而能够有效减小结构残余变形。

图8 10条地震波作用下框架最大层加速度的平均值

图8为10条地震波作用下两种框架的最大楼层加速度均值。由图8可知，SCFED框架的楼层加速度明显大于BRB框架，这主要是由于SCFED旗帜型的滞回曲线特点所导致的。在自复位力的作用下，当支撑回复到初始位置附近时速度较快，且刚度转换较剧烈，而同一节点相邻的几个支撑运动并不同步，导致节点产生较大的不平衡力，只能由惯性力来平衡，致使层加速度变大。加速度过大可能对一些对加速度敏感的非结构部件造成不利影响，这一点在设计SCFED框架结构时应予以考虑。

5 结 论

本文采用OpenSEES有限元软件，通过与BRB框架结构的对比，研究了SCFED框架结构的抗震性能，得到如下结论：

(1) 由于自复位体系提供的第二刚度，SCFED框架在结构屈服后的刚度明显高于BRB框架结构；

(2) SCFED框架的最大层间位移角小于BRB框架，且沿高度分布较均匀；而BRB框架的损伤集中系数较大，不能有效抑制薄弱层的形成；

(3)针对本文的框架模型，BRB框架平均残余层间位移角约为最大位移角的10%～20%，而SCFED框架的残余位移角仅为最大位移角的1%～2%，表明SCFED能有效控制结构的残余变形。

(4) 由于SCFED滞回性能的特点，在支撑回归到初始位置时刚度转换剧烈，导致结构层加速度较大，在设计SCFED框架时应予以注意。

[1] 郭 彤, 宋良龙, 张国栋,等. 腹板摩擦式自定心预应力混凝土框架梁柱节点的试验研究[J]. 土木工程学报, 2012, 45(6): 23-32.

[2] Chi H, Liu J. Seismic behavior of post-tensioned column base for steel self-centering moment resisting frame[J]. Journal of Constructional Steel Research, 2012, 78(2): 117-130.

[3] Christopoulos C, Tremblay R, Kim H J, et al. Self-centering energy dissipative bracing system for the seismic resistance of structure: development and validation[J]. Journal of Structural Engineering, 2008, 134(1): 96-107.

[4] 高 杰, 薛彦涛, 王 磊. 屈曲约束支撑(JY-SD型)在抗震加固中的应用[J]. 土木工程与管理学报, 2011, 28(3): 339-343.

[5] Ohtori Y, Christenson R E, Spencer B F, et al. Benchmark control problems for seismically excited nonlinear buildings[J]. Journal of Engineering Mechanics, 2004, 130(2): 366-385.

[6] 赵 林. 屈曲约束支撑钢框架设计及抗震性能研究[D]. 西安: 西安建筑科技大学, 2011.

[7] 曲 哲, 叶列平, 潘 鹏. 建筑结构弹塑性时程分析中地震动记录选取方法的比较研究[J]. 土木工程学报, 2011,44(7): 10-21.

[8] Erochko J, Christopoulos C, Tremblay R, et al. Residual drift response of SMRFs and BRB frames in steel buildings designed according to ASCE 7-05[J]. Journal of Structural Engineering, 2011, 137 (5): 589-599.

[9] Sabelli R, Mahin S, Chang C. Seismic demands on steel braced-frame buildings with buckling-restrained braces[J]. Engineering Structures, 2003, 25(5): 655-666.

[10] Kiggins S, Uang C. Reducing residual drift of buckling-restrained braced frames as a dual system[J]. Engineering Structures, 2006, 28(11): 1525-1532.