移动荷载下机场刚性道面惰性点影响因素分析

刘 锋, 孙明清, 王应军

(武汉理工大学 理学院，湖北 武汉 430070)

随着时间的推移，水泥混凝土路面在使用过程中都会出现或多或少的病害，因此，众多学者开始关注水泥混凝土路面剩余寿命的计算问题。但路面剩余寿命的计算必然涉及到道面面层的弹性模量和地基反应模量的反算问题，目前，路面结构反算的主要方法有：图表法、回归公式法、迭代法、数据库搜索法、神经网络法和遗传算法等。各种方法无法同时解决反算问题的初始值和局部收敛问题、解的唯一性问题和反算结果的合理性问题[1]。2000年，同济大学孙立军教授和日本运输部港湾技术研究所八谷好高教授共同提出了一种新的解决路面结构反算问题的方法—惰性弯沉法[2，3]，此方法将道面结构反算分析的两个基本参数E(面层板弹性模量)和k(地基反应模量)分开独立求解，这样便避开了两者的相互干扰，也极大地提高了路面结构反算精度，很好地解决了路面结构反算的后两个问题。

图1 不同模量对应的弯沉盆及其交点

据文献[2]、[3]和图1可知，在道面层厚度不变、地基反应模量不变和相同荷载情况下，面层模量越大,荷载的扩散能力越强,弯沉盆越平坦；面层模量越小,荷载的扩散能力越弱,弯沉盆越陡。即荷载附近的弯沉随着面层模量的增大而减小,而远离荷载的弯沉随着随着面层模量的增大而增大,这样两个模量不同的弯沉盆必然相交于一个与面层模量无关的点，此点称为惰性点。惰性点距荷载中心的距离称为惰性点距离，记作RC；惰性点处的弯沉称为惰性点弯沉，记作DC。

随着激光技术在道路检测中的应用，如图2所示的滚轮式弯沉仪(RWD)[3，4]应运而生。RWD是利用具有一定移动速度的车辆自身对道面施加荷载，然后通过激光检测装置检测道面动态弯沉响应的仪器，RWD更加符合实际情况，而惰性弯沉法是建立在静荷载分析基础上的回归分析方法，本文将对道面结构在移动荷载作用下惰性点的存在性及其影响因素展开研究，从而为惰性点理论在RWD反算中的应用奠定基础。

图2 滚轮式弯沉仪

1 Kirchhoff薄板运动微分方程

利用薄板微分单元的力学平衡条件可以得到薄板在任意荷载作用下的薄板振动微分方程(1)。

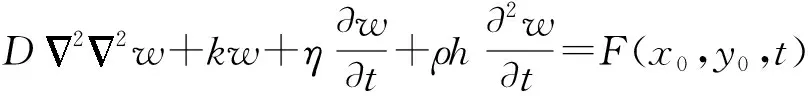
(1)

根据文献[5]可知，考虑荷载以速度c运动，使用随荷载运动的坐标系xOy(x=x0-ct,y=y0)代替原坐标系x0Oy0,则式(1)变为：

(2)

该问题的边界条件为：

(3)

式中：n=0,1,2,…。

式(2)可以通过Fourier变换法求解，而Fourier的变换式可以定义为式(4)和式(5)。对式(2)进行三维Fourier变换就可以得到式(6)，即可以得到任意匀速运动荷载作用下Kelvin地基上无限大板稳态挠度的一般解。

e-i(k1 x+k2 y+wt)dxdydt

(4)

ei(k1 x+k2 y+ωt)dk1dk2dω

(5)

(6)

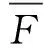
行驶中的车辆轮胎与地面的接触面通常简化为矩形接触面。而这种移动矩形均布荷载的数学表达式为(7)。

(7)

式中：P为荷载；2l1、2l2分别为荷载在平行于和垂直于运动方向的分布长度；H(·)为单位阶梯函数；f(t)为荷载集度随时间变化函数。

本文的如下分析是基于恒载的分析，因此，对式(7)进行Fourier变换并令式(7)中的f(t)=1，得出移动矩形均布恒载作用下板稳态扰度的解析解[5]为

(8)

式中：i为虚数单位。

从式(8)可知，在移动均布恒载作用下，道面结构的弯沉受车辆行驶速度、板厚、泊松比、密度和地基阻尼等因素影响。鉴于扰度解析解的复杂性以及数据提取的方便，本文将结合有限元数值分析方法研究移动荷载下道面结构惰性点的存在性及其受各种因素影响的规律，从而为惰性弯沉法在移动荷载下道面结构参数反演回归分析中奠定基础。

2 三维道面力学模型

2.1 基本假设

对道面进行三维力学分析时，通常进行如下的基本假设：

(1)面层和土基的材料均假设是线弹性材料，均符合广义虎克定理；

(2)道面各结构层厚度是有限的，而在水平方向上是无限的。据文献[6]和[7]，对于道面动力学性能分析，土基厚度取大于12米时，实际测量值与理论分析值相近，基本满足计算要求；

(3)道面各结构层之间是完全接触无滑移；

(4)荷载垂直作用于道路面层，在距离荷载无限远处和无限深处路面结构的应力、应变和位移均为零。

2.2 三维道面有限元模型

2.2.1道面有限元模型

公路道面通常为矩形板块，而机场道面通常为正方形板块，故在ANSYS中使用BLOCK块命令来建立道面的面层有限元模型，采用SOLID45单元划分道面结构面层网格模型。地基通常简化为三种模型形式：Winkler地基模型、弹性半空间地基模型和弹性层状体系模型。在ANSYS分析中，使用弹簧单元COMBIN14或LINK10单元模拟Winkler地基。图3为道面结构横向断面图，图4为网格划分完成后的整体道面结构有限元模型。在三维道面结构有限元分析中，模型的约束条件可假定为Winkler地基底部的节点位移固定约束，道面板的四个侧面约束法向方向位移[8，9]。

图3 道面结构横向断面

图4 网格划分完成后的道面ANSYS模型

2.2.2轮胎与路面接触面换算

文献[10]认为，每个轮胎与路面的接触面由两个半圆形和一个矩形组成(如图5所示)，但为了简化计算，黄仰贤教授提出可以使用一个矩形代替前者轮胎与路面的接触形状，而由此产生的计算误差很小。

图5 轮胎与路面接触面换算

2.2.3移动荷载施加

在ANSYS中，移动荷载使用“移动荷载带”的方法进行模拟分析，即每隔一段时间轮胎所占矩形面积向前移动一格(如图6所示)，直到最终车轮移动荷载移出整个道面板块为止[11]。在本文中，车辆移动荷载简化为1 MPa的移动均布荷载。

图6 移动荷载带

2.2.4计算数据的提取

本文中不同面层板弹性模量下对应的弯沉盆数据是在移动荷载移动至板中心O时，提取如图6中O点以右的弯沉数据。而惰性点参数则按如下步骤确定：首先，根据弯沉盆曲线方程求出两两相交弯沉盆曲线交点坐标(即：惰性点参数RC和DC)；其次，分别求取RC和DC的平均值初步估算惰性点参数；最后，根据惰性点参数确定原则[2](面层板弹性模量变化时，某点的弯沉值变化在±1.5%时所对应的弯沉值即为惰性点弯沉，而此点所对应的弯沉距离即为惰性点距离)最终确定惰性点参数。

3 物理因素对惰性点的影响分析

3.1 车辆行驶速度

车辆的行驶速度对道面板弯沉的影响是不言而喻的。本文选取了50～65 km/h中的部分速度点分析了车辆行驶速度对道面板惰性点参数的影响，分析结果见图7和图8所示。图7表示在不同车速、不同面层弹性模量和相同地基反应模量下的道面结构弯沉盆曲线族。从图7的分析结果可知，与静荷载作用于道面板结构存在惰性点一样，在不同速度的移动荷载作用下，刚性水泥混凝土道面结构依然存在一个与面层板弹性模量无关的小区域，此区域的宽度范围大约在10 cm左右，因此，可以依据惰性点确定原则将此区域缩小为一个点，此点可称为动力惰性点。随着车速的增加，相同弹性模量弯沉盆曲线，在动力惰性点左边，弯沉盆曲线的弯沉值(绝对值)均在减小，而在动力惰性点右边，弯沉盆曲线的弯沉值(绝对值)均在增大。而从图8的分析得知，随着移动荷载速度的增大，惰性点的距离和惰性点弯沉均呈现出减小的趋势，且变化较大。因此，速度对惰性点参数有较大影响。

图7 不同车速和不同面板弹性模量下的道面结构弯沉盆曲线族

图8 惰性点参数随车速变化曲线

3.2 面层板厚度

据文献[2]可知，在静荷载作用下道面板结构惰性点参数受道面结构面层厚度的影响很大，通常，随着道面板面层厚度增大，惰性点的距离会增大，而惰性点的弯沉会减小。静荷载下，面层板厚度的增大意味着道面板板体整体刚性的提升，因此，板体中心的弯沉值会降低，荷载对板体的影响范围也会更远。从图9可知，移动荷载在以60 km/h的速度移动时，相同面层板弹性模量下，道面板结构中心点O处的弯沉值随着板厚度的增大而减小，而远离荷载中心O点的道面板弯沉值则随着板厚度的增大而增大。因此，道面板结构惰性点距离随着面板厚度的增大而增大，而惰性点弯沉则随着面板厚度的增大而减小，惰性点参数值在不同面层板厚度时，变化较大，如图10所示。因此，面层板厚度对惰性点参数有较大影响。

3.3 面层板泊松比

根据文献[12]可知，水泥混凝土的泊松比通常是在0.15～0.25之间变化。具有不同泊松比的面层板，当移动荷载以60 km/h的速度在其上移动时，根据图11可知，惰性点距离随着面层板泊松比的增大仅有微小的增大，最大差值约为8.83 mm；而惰性点弯沉值随着面层板泊松比的增大仅有很微小的减小，最大差值约为1.21 μm。因此，面层板泊松比对惰性点参数的影响十分微小，可以忽略不计。

3.4 面层板密度

水泥混凝土的密度变化范围为2350～2500kg/m3。通过分析可知，具有不同密度的面层板，当移动荷载以60 km/h的速度在其上移动时，密度的变化会对道面结构弯沉盆曲线有影响，这与薄板振动微分方程的分析结果是相同的，但根据图12可知，惰性点距离随着面层板密度的增大仅有微小的减小，最大差值约为9.32 mm；而惰性点弯沉值随着面层板密度的增大也仅有微小的减小，最大差值约为0.15 μm。因此，面层板密度对惰性点参数的影响十分微小，可以忽略不计。

图9 不同面层板厚度和不同面板弹性模量下的道面结构弯沉盆曲线族

图10 惰性点参数随面层板厚度变化曲线

图11 惰性点参数随面层板泊松比变化曲线

图12 惰性点参数随面层板密度变化曲线

3.5 地基阻尼

对基于Winkler地基的刚性水泥混凝土道面板进行动力学性能分析时，地基部分通常涉及两个基本参数：地基反应模量和地基阻尼。根据Winkler地基基本原理[12]，在进行道面板的动力学数值仿真分析时，将地基反应模量转换为弹簧的弹性系数来考虑，而对于弹簧单元而言，由于其有弹性系数和阻尼系数两个基本参数，因此，在本文的分析中，将地基整体阻尼参数分解到每个弹簧单元的方法来考虑地基的阻尼问题，而进行刚性道面的动力学分析的地基阻尼范围取为0～1.8×108N·s/m3，根据图13的分析结果可知，具有不同地基阻尼的刚性道面板，当移动荷载以60 km/h的速度在其上移动时，惰性点距离随着地基阻尼的增大仅有微小的减小，最大差值约为5.45 mm；而惰性点弯沉值随着地基阻尼的增大也仅有很微小的减小，最大差值约为1.69 μm。因此，地基阻尼对惰性点参数的影响十分微小，可以忽略不计。

图13 惰性点参数随地基阻尼变化曲线

4 结 论

结合Kirchhoff薄板运动微分方程，并通过对Winkler地基上的单层刚性混凝土板加载移动荷载进行了大量的有限元分析，得出以下结论：

(1)移动荷载下，Winkler地基上的机场刚性道面板存在一个与面层板弹性模量无关而与地基反应模量有关的动力惰性点。

(2)移动荷载下，面层板的厚度、泊松比、密度、地基阻尼和车辆行驶速度等对惰性点参数(即：惰性点距离RC和惰性点弯沉DC)均有影响。分析结果表明：面板的泊松比、密度和地基阻尼对惰性点参数影响十分微小，可以忽略不计；但面层板的厚度和车辆行驶速度对惰性点参数影响较大,在进行动态惰性点参数回归分析时不可忽略不计。

[1] 查旭东.路面结构层模量反算方法综述[J].交通运输工程学报,2002,2(4), 1-6.

[2] 孙立军,八谷好高,姚祖康.水泥混凝土路面板模量反算的一种新方法—惰性弯沉法[J].土木工程学报，2000,33(1),83-87.

[3] 孙立军.道路与机场设施管理学[M].北京：人民交通出版社,2009.

[4] Elseifi M A, Dasari K, Abdel-Khalek A, et al. Development of the triangular model for pavement evaluation using the rolling wheel deflectometer[J]. Journal of Transportation Engineering, 2013, 139(3), 313-320.

[5] 蒋建群,周华飞,张土乔.移动荷载下粘弹性地基上无限大板的稳态响应[J].中国公路学报, 2006,19(1),6-11.

[6] Siddhartha Raj V, Yao Jian, Sebaaly Peter E. Pavement strain from dynamic 3D load distribution [J]. Journal of Transportation Engineering, 1998, 126(9), 557-566.

[7] 钱振东,张 磊,陈磊磊.路面结构动力学[M].南京：东南大学出版社,2010.

[8] Liu Feng, Sun Mingqing, Wang Yingjun,et al. Numerical Method for Calculation of the PCN of Airport Pavement[C]// ICTIS 2013: Improving Multimodal Transportation Systems - Information, Safety, and Integration - Proceedings of the 2nd International Conference on Transportation Information and Safety. Virginia:ASCE, 2013:1763-1769.

[9] 杨绍普,陈立群,李韶华.车辆-道路耦合系统动力学研究[M].北京：科学出版社,2012.

[10] 黄仰贤.路面分析与设计[M].余定选，齐 诚，译.北京：人民交通出版社,1998.

[11] 侯 芸,孙四平,郭忠印.移动荷载下刚性路面响应的参数影响分析[J].同济大学学报(自然科学版),2003,31(1),31-35.

[12] 黄 义,何芳社.弹性地基上的梁、板、壳[M].北京：科学出版社,2005.