多轴承支撑轴系的精确变形计算研究

刘越,周广明,张祖智,杜万里,马贵叶

(中国北方车辆研究所车辆传动重点实验室,北京 100072）

多轴承支撑轴系的精确变形计算研究

刘越,周广明,张祖智,杜万里,马贵叶

(中国北方车辆研究所车辆传动重点实验室,北京 100072）

针对传动系统中典型的多轴承支撑轴系结构,提出了轴和轴承刚度耦合建模方法以及轴系结构精确变形迭代求解方法。基于轴承几何学、接触力学理论,采用Newton-Raphson算法实现轴承接触应力和变形计算、轴承内部载荷分配计算、轴承滚动体力学平衡方程组的求解,建立轴承刚度矩阵。实现轴承与Timoshenko梁的刚度耦合,形成轴系刚度矩阵,并通过松弛迭代法求解稀疏刚度矩阵。改变轴承刚度矩阵完成迭代过程,获得系统的精确变形。通过算例,验证了该计算方法收敛快、对初值要求低,计算精度较高。

固体力学;矩阵位移法;Timoshenko梁;轴承刚度;SSOR迭代法;Newton-Raphson算法

0 引言

获取轴和轴承精确的变形量,是正确预测轴承和齿轮疲劳寿命的基础,对轮齿齿面精细化设计具有重要意义[1-2]。

传统计算变形量的方法将轴承作为刚性支撑点,根据受力平衡条件、虚位移原理等建立方程组,求解轴承的支撑反力和变形。这种方法虽然简便,却无法得到轴承的准确受力情况,也就无法计算轴和轴承的精确变形。事实上,轴和轴承刚度大小和变形量是相互影响的,无法独立计算得到轴和轴承的精确变形[3]。因此,只能将轴和轴承作为整体进行系统分析。

目前,国内有关轴承刚度的研究较多[4-9],文献[4-5]采用拟静力学方法建立了角接触球轴承刚度矩阵,文献[6]通过实验验证了拟静力学方法求解轴承刚度矩阵的准确性。但对传动系统中的多轴承支撑轴系变形的研究较少,仍处于探索阶段。文献[7]对多支点轴系中滚动轴承进行了拟静力学分析,将常见的阶梯轴等效转化为理想的等截面轴,需求解多个复杂的非线性方程组,方程数目庞大,迭代复杂。文献[8]需要借助有限元软件完成轴和轴承的刚度迭代,建立轴系的有限元模型使得计算效率和通用化程度受到较大的限制。相比而言,国外这方面的研究比较成熟[9-13],已相继开发出了相关的商业软件和专用软件,如Masta、Romax、Kissoft,这些软件在工程设计中得到了良好的运用。

1 基本方程

图1为传动系统中典型的多轴承支撑轴系结构。有3个滚球轴承作为支撑,轴端受主动力矩,齿轮处作用在轴上的载荷有径向力、切向力和被动力矩。轴系采用直角坐标系,坐标原点O为轴上端面圆心,所在端面为YOZ面,旋转轴为X轴。

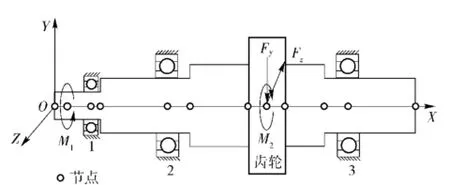
图1 轴系统结构图Fig.1 Shafting model

1.1 阶梯轴的有限元法计算

将阶梯轴简化为梁单元既能节省计算时间,又能满足精度要求。由于传动系统中多为短粗轴,为充分考虑剪切力对轴系变形的影响,选用Timoshenko梁作为分析单元。

考虑剪切变形影响后,Timoshenko梁的应变能方程为

将单元节点变量变成两部分,即

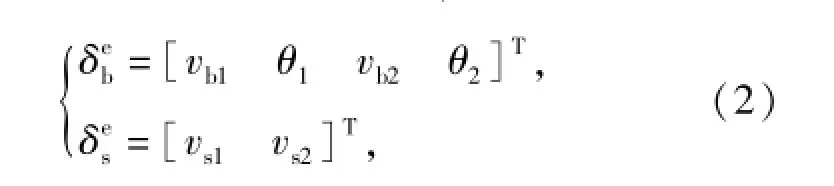
对于弯曲变形引起的位移采用Hermite形函数插值表示,剪切引起的位移采用线性插值法,即有

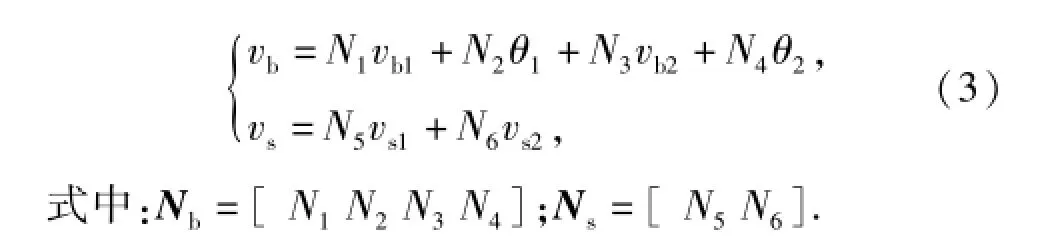
将(3)式代入(1)式中,弯曲部分的应变能Ub:

剪切部分的应变能Us:

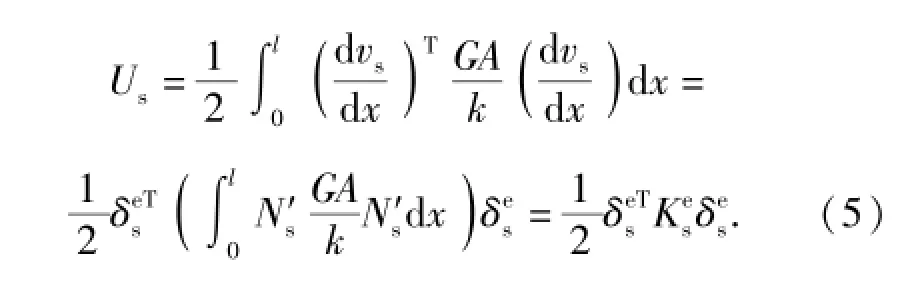
将Hermite形函数代入(4)式和(5)式中,得到Timoshenko梁的弯曲刚度矩阵和剪切刚度矩阵.

对单元刚度矩阵进行叠加,形成轴刚度矩阵,为(6×nShaft)×(6×nShaft)(nShaft为轴上节点个数)阶的对称性带式稀疏矩阵。图2为叠加过程示意图,其中单元1和单元2分别为梁单元刚度矩阵,并且两个单元通过节点2连接。

1.2 滚动轴承的刚度矩阵获取

由于滚动轴承的受载滚动体个数与所受载荷的大小和方向有关,因此轴承刚度具有非线性特点。以球轴承为例,在无载荷状态下,初始接触角定义为

式中:A=B×D,B=fi+fo-1,fi、fo分别为内外滚道的沟曲率半径系数,D为滚球直径;Pd为径向游隙。

图2 刚度矩阵耦合Fig.2 Stiffness matrix coupling

如图3所示,在轴向力Fa和径向力Fr的作用下,轴承内圈产生轴向位移δa和δr,δa和δr为沿接触线法向位移δn的分量。δn由(7)式确定:

受载后的接触角αj为

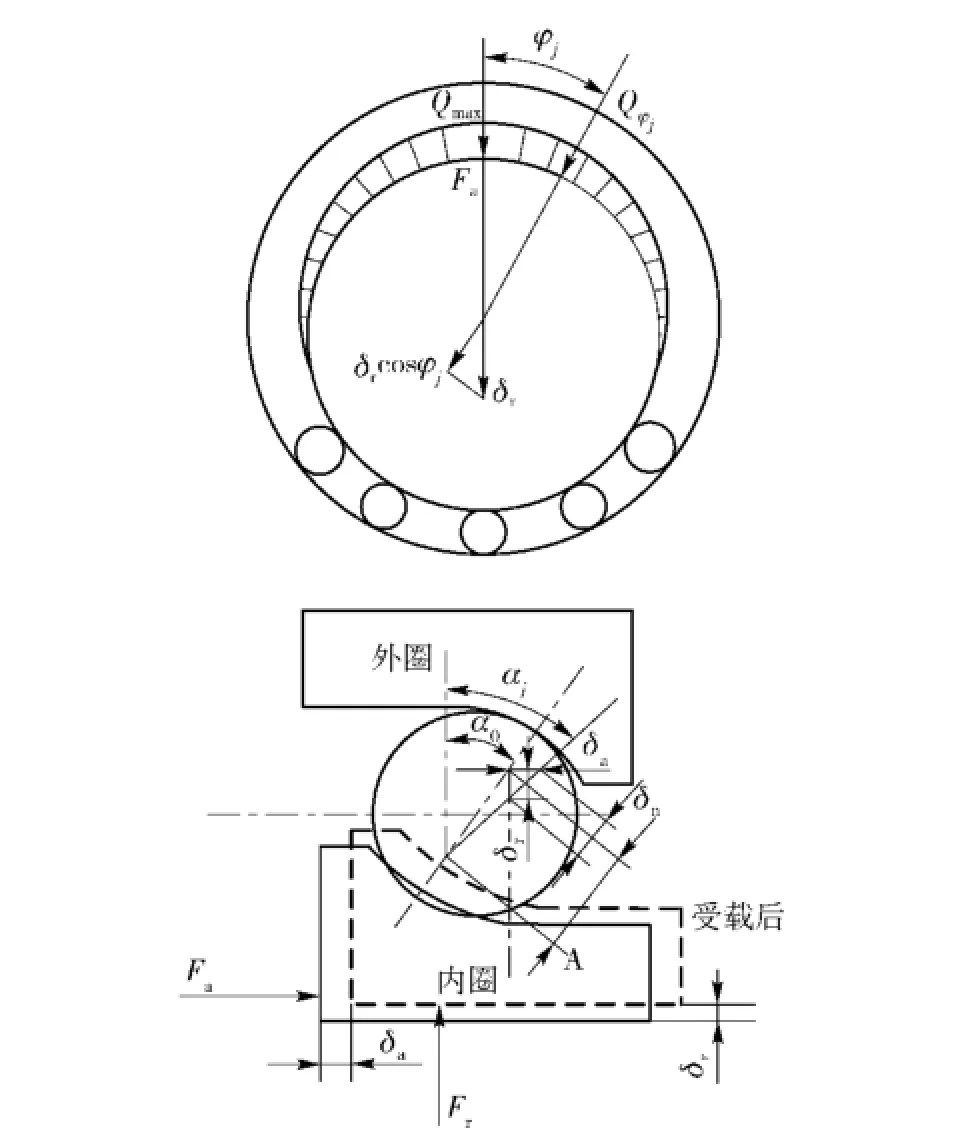
图3 径向和轴向力作用下的角接触球轴承Fig.3 Angular contact ball bearing under the action of the radial and axial forces

根据Hertz理论,球轴承受载的接触区域为旋转椭圆面,计算椭圆长半轴和短半轴之比χ需要求解一个含有第一类和第二类完全椭圆积分的超越方程,如(9)式、(10)式所示[2]:

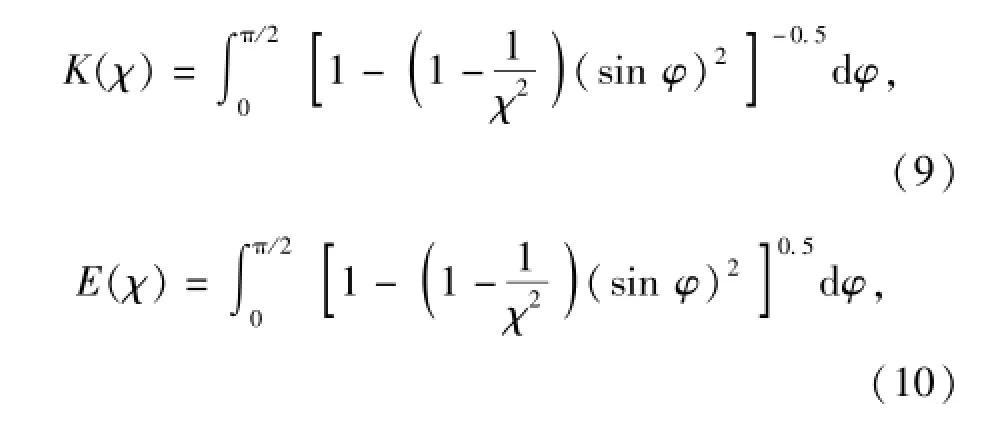
式中:两类椭圆积分K(χ)、E(χ)和椭圆接触区长短半轴之比χ满足方程式(11)式,求解方程可得到χ:

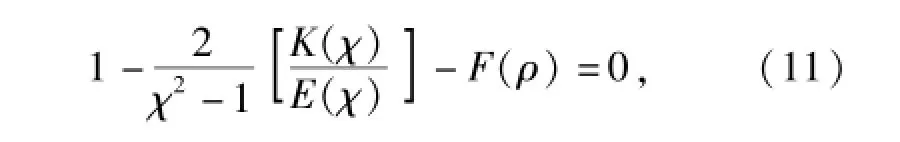
式中:F(ρ)为滚球和滚道的曲率差。

根据文献[2]中的理论,滚球轴承中滚动体受力Q与变形δ满足:

根据滚动体的受载—变形关系,求解轴承所受外力与滚球作用力的平衡方程组(14)式和(15)式:

图4 轴承变形的几何参数Fig.4 Geometric parameters of bearing deformation

在原轴承位移量δ的基础上取较小位移变量Δ,计算轴承反力,得到轴承刚度矩阵。

1.3 轴和轴承的刚度耦合计算

在多轴承支撑的轴系分析中,轴承内圈的位移和轴配合节点处的位移满足变形协调关系。把轴承单元作为变刚度的弹簧单元,其中一个节点(轴承内圈)与轴配合节点耦合;另外一个节点(轴承外圈)为输入的边界条件。如轴承外圈与箱体配合,若箱体变形可忽略不计,外圈节点的位移列阵置零;反之,可将箱体的变形量作为外圈的位移。将图1所示的轴系简化为计算模型,如图5所示。

图5 模型简化图Fig.5 Simplified shafting model

按照图2所示的刚度耦合方法,将轴承与轴的刚度矩阵耦合,形成包含轴承——轴的系统刚度矩阵。

2 算法

求解轴承刚度时,需要对(14)式和(15)式所形成的5个非线性方程组求解。以轴承内圈中心五自由度作为未知量,采用Newton-Raphson算法,利用梯度估计函数与自变量的截距,进行多维求根。

初值的选取对非线性方程组的求解至关重要,为有较好的计算结果,预设轴承刚度K0,通过X0= K-10F得到计算初值。

对(14)式和(15)式表示的5个非线性方程组进行泰勒展开:

令Jij=∂Fi/∂xj,得到偏导数在i点的雅克比矩阵Ji.

用矩阵形式表示(16)式为

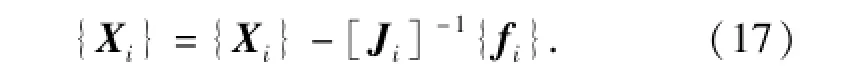
解线性方程组(17)式得到修正量ΔX,然后进行第二次计算,使X2=X+ΔX,至此,迭代过程产生。通过设置允许误差ε,判断是否结束计算。

根据叠加生成系统总体刚度矩阵KS,建立系统力学平衡方程式(18)式:

耦合生成的刚度矩阵KS为稀疏矩阵,采用直接法(如高斯消元法)求解方程组会破坏稀疏矩阵特性,产生较大的舍入误差,影响计算结果,迭代过程难以收敛。采用SSOR迭代法取得了良好的计算效果。设刚度矩阵KS=I-L-U,SSOR的迭代方法如下:

式中:I、U、L分别是刚度矩阵KS的对角阵、下三角和上三角矩阵;S为SSOR的迭代矩阵,

计算方法采用变轴承刚度的计算思路。算法如图6所示。

通过对轴承刚度的迭代,最终达到轴系力学平衡。迭代过程中通过轴和轴承的变形协调位移大小调节轴承的刚度值,不断逼近目标结果。

3 算例

将图1所示的结构作为算例,采用传统方法和开发程序进行计算结果对比。轴的材料为合金钢,材料参数如下:弹性模量E=206 000 MPa,切变模量G= 79380 MPa,泊松比ν=0.3.载荷条件如下:轴端处输入扭矩1000 000 N·mm,齿轮所受载荷Fy=-2 426.5 N, Fz=-6 666.7 N,Mx=-1 000 000 N·mm,轴承外圈固定。

图6 计算框图Fig.6 Computation block diagram

轴和轴承的结构尺寸如表1和表2所示。

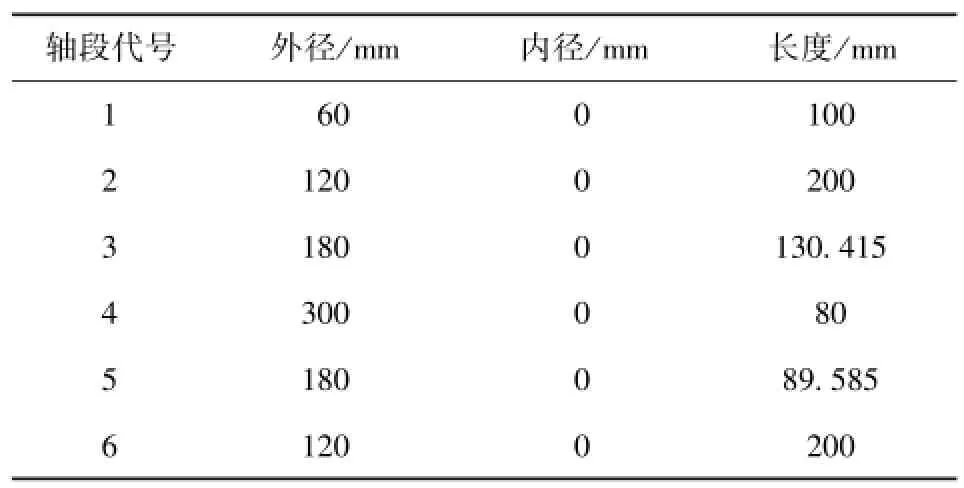
表1 轴的尺寸参数Tab.1 Dimension parameters of shafts

采用传统力学方法,将结构简化为图7所示的超静定梁,其中,轴承视为刚性支撑点。运用矩阵位移法计算该结构的支反力,得到支座1的反力Fy1= -250.4 N,Fz1=-688.0 N,支座2的反力Fy2= 1688.9 N,Fz2=4640.1 N,支座3的反力Fy3=988.0 N, Fz3=2 714.5 N.

根据本文提出的计算思路和算法,对算例所示结构作为轴系结构进行计算。将Y方向轴承主刚度KrY的迭代过程绘制为图表,如图8所示。此时,各轴承的径向支撑反力为:轴承1的支撑反力Fy1= 605.5 N,Fz1=1 299.2 N;轴承2的支撑反力Fy2= 470.8 N,Fz2=1 808.7 N;轴承3的支撑反力Fy3= 1 351.7 N,Fz3=3 558.8 N.

图7 材料力学方法简化模型Fig.7 Simplified model for mechanics of materials

图8 轴承刚度迭代过程Fig.8 Bearing stiffness iteration

对比上述两种方法得到的计算结果可知,轴承的弹性变形不容忽略。轴承的实际刚度不仅会影响外载荷在各轴承上的载荷分配,甚至可以改变轴承的受力方向。

在国外先进的商业软件中建立图1所示的模型,轴的材料选取合金钢,材料参数设置为算例中的参数,轴承选取表2所示的轴承,进行变形计算。与依照本文提出的计算方法开发的程序进行结果对比,图9和图10为轴系线位移和角位移结果对比情况。

图9 轴的线位移结果对比Fig.9 Linear displacement of shaft

从图9和图10可以看出,本文计算方法与商业软件的计算结果吻合度很高,线位移中3轴承节点处的位移误差均在1 μm以内,其余节点处的位移也均在1.5 μm以内。所有节点处的角位移误差均在0.002 mrad以内。因此,完全满足工程应用。

4 结论

通过上述分析,可以得到如下结论:

1)在多轴承支撑轴系的变形分析中,轴承的弹性变形对轴承的受力分配影响很大。采用轴和轴承的刚度耦合联合计算,比单独计算轴和轴承变形更符合实际情况。

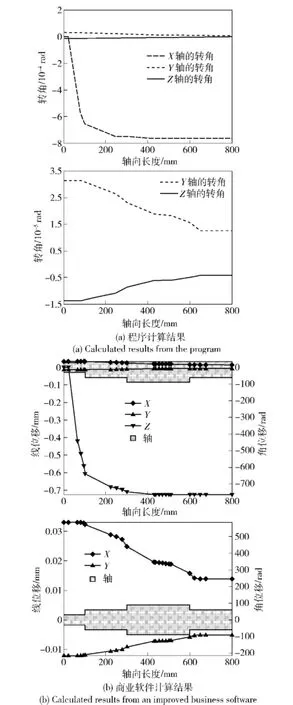
图10 轴的角位移结果对比Fig.10 Angular displacement of shaft

2)在迭代求解轴承变形的过程中,提出了以轴承内圈中心位移为未知量的五维求根算法。相对于以滚子变形作为未知量的常规算法,避免了大量非线性方程组的求解,提高了计算稳定性,具有收敛快、初值要求低、准确度高的特点。

References)

[1] 罗继伟,罗天宇.滚动轴承分析计算与应用[M].北京:机械工业出版社,2009.

LUO Ji-wei,LUO Tian-yu.Rolling bearing analysis and calculation[M].Beijing:China Machine Press,2009.(in Chinese)

[2] Harris T A,Kotzalas M N.滚动轴承分析:轴承技术的基本概念[M].5版.罗继伟,马伟,杨咸启,等,译.北京:机械工业出版社,2010.

Harris T A,Kotzalas M N.Rolling bearing analysis:Essential Concepts of Bearing technology[M].5th ed.LUO Ji-wei,Ma Wei,YANG Xian-qi,et al,translated.Beijing:China Machine Press,2010.(in Chinese)

[3] Redmond I.Study of a misaligned flexibly coupled shaft system having nonlinear bearings and cyclic coupling stiffness—theoretical model and analysis[J].Journal of Sound and Vibration,2010, 329(6):700-720.

[4] 谢涛,刘品宽,陈在理.转台轴系轴承刚度矩阵的理论推导与数值计算[J].哈尔滨工业大学学报,2003,35(3):329-333.

XIE Tao,LIU Pin-kuan,CHEN Zai-li.Theoretical analysis and numerical estimation of stiffness matrix of angular contact ball bearing in a spindle-bearing system[J].Journal of Harbin Institute of Technology,2003,35(3):329-333.(in Chinese)

[5] 黄浩,张鹏顺,温建民.航空发动机角接触球轴承刚度的一种实用分析方法[J].南京航空航天大学学报,2000,32(4): 422-427.

HUANG Hao,ZHANG Peng-shun,WEN Jian-min.An analytical method of stiffness for angular contact ball bearing of aeroengine [J].Journal of Nanjing University of Aeronautics&Astronautics, 2000,32(4):422-427.(in Chinese) [6] 方兵,张雷,曲兴田,等.角接触球轴承刚度理论计算与实验[J].吉林大学学报:工学版,2012,42(4):840-844.

FANG Bing,ZHANG Lei,QU Xing-tian,et al.Theoretical and experimental research of stiffness of angular contact ball bearing [J].Journal of Jilin University:Engineering Edition,2012,42 (4):840-844.(in Chinese)

[8] 罗祝三,吴林丰.多支点轴系中滚动轴承的拟静力学研究[J].南京航空航天大学学报,1995,27(3):291-298.

LUO Zhu-san,WU Lin-feng.Quasi-static analysis of multi-bearing shaft system[J].Journal of Nanjing University of Aeronautics& Astronautics,1995,27(3):291-298.(in Chinese)

[9] 刘显军,洪军,朱永生,等.多支撑轴系轴承受力与刚度的有限元迭代计算方法[J].西安交通大学学报,2010,44(1):41 -45.

LIU Xian-jun,HONG Jun,ZHU Yong-sheng,et al.Iterative method to solve bearing's force and stiffness for a multi-support spindle system based on finite element analysis[J].Journal of Xi' an Jiaotong University,2010,44(1):41-45.(in Chinese)

[10] 刘卫群,罗继伟,吴长春,等.滚动轴承刚度分析程序[J].计算力学学报,2001,18(3):375-378.

LIU Wei-qun,LUO Ji-wei,WU Chang-chun,et al.Program for the stiffness analysis of rolling bearing[J].Chinese Journal of Computational Mechanics,2001,18(3):375-378.(in Chinese)

[11] Palmgren A.Ball and roller bearing engineering[M].3th ed. Burbank,Philadephia:SKF Industries Inc,1959.

[12] Ding J,Krodkiewski J M.Inclusion of static indetermination in the mathematical model for non-linear dynamic analyses of multibearing rotor system[J].Journal of Sound and Vibration,1993, 164(2):267-280.

[13] Zverv I,Pyoun Y S,Lee K B,et al.An elastic deformation model of high speed spindles built into ball bearings[J].Journal of Materials Processing Technology,2005,170(3):570-578.

Accurate Calculation for Deformation of Multi-bearing Shafting System

LIU Yue,ZHOU Guang-ming,ZHANG Zu-zhi,DU Wan-li,MA Gui-ye
(Science and Technology on Vehicle Transmission Laboratory,China North Vehicle Research Institute,Beijing 100072,China)

A new modeling method of shaft-bearing stiffness coupling and an iterative method for calculating the deformation of multi-bearing shafting system are presented for the typical complex multi-bearing shafting system used in driving system.The bearing stiffness matrix is created by Newton-Raphson method through the following steps:calculation of contact stress and deformation,calculation of internal load distribution,and solution of rolling elements mechanics equilibrium equations,which is based on the theory of bearing geometry and contact mechanics.The shafting system stiffness matrix is constructed by coupling the Timoshenko beam and bearings.The deformation of system can be solved by iterative matrix displacement method of variable bearing stiffness,which is applied to SSOR iterative matrix.It is proven that the method has better convergence,lower demand to initial data,and higher accuracy,which is more convenient to use for engineering design.

solid mechanics;matrix displacement method;Timoshenko beam;bearing stiffness;SSOR iterative matrix;Newton-Raphson method

TP391

:A

1000-1093(2014)03-0305-07

10.3969/j.issn.1000-1093.2014.03.003

2013-09-08

国防科技工业技术基础科研项目(2009b2542134);车辆传动重点实验室基金项目(9140C340103120C34124)

刘越(1986—),男,工程师。E-mail:liuyue1620@sina.com