船用柴油机曲轴疲劳分析方法研究

2014-06-27，，

船海工程 2014年3期

，，

(1.驻沪东中华造船集团有限公司军代表室，上海 200129;2.沪东重机有限公司，上海 200129)

近年来，曲轴的疲劳研究受广泛关注。随着对内燃机动力性能和可靠性能要求的不断提高，曲轴强度的重要性更加突出，为了能使计算的结果更符合实际，国内外学者对于曲轴疲劳强度的研究已经做了大量的工作[1-5]。然而，对于曲轴复杂载荷的获取一直没有很好地解决[6-8]，如何提取多体动力学的分析结果以及疲劳模型的创建方法一直是柴油机曲轴疲劳研究的技术难题。为此，本文分别采用简化法、协同法对某船用柴油机曲轴进行疲劳分析。

1 有限元模型

1.1 网格模型

该曲轴用于某船用柴油机，见图1。

图1 曲轴实物照片

柴油机为四冲程12缸V型机，最大爆压为25 MPa，主要用于推进船舶和发电。运行过程中，曲轴承受着由缸内燃气作用力、往复惯性力及旋转惯性力引起的周期性变化的交变载荷，并对外输出转矩。这种交变载荷会引起曲轴的疲劳失效。

柔性体生成时要考虑到计算的精度以及在分析过程中载荷的施加以及约束方式。曲柄销和主轴颈处采用二阶楔形单元，与曲柄臂处的二阶四面体单元形成很好的过渡。曲柄销和主轴颈外层外圈设置两层单元是为了在施加载荷和约束的时候能正确模拟实际情况，选择合适的单元进行约束以及施加载荷。在曲柄销、主轴颈与曲柄臂连接处加密处理是考虑到应力集中问题。本模型包含61 494个单元，其中四面体44 364个，楔形单元17 130个，单元类型分别为C3D10I和C3D15，并对曲柄销和主轴颈处分别耦合，有限元模型见图2。

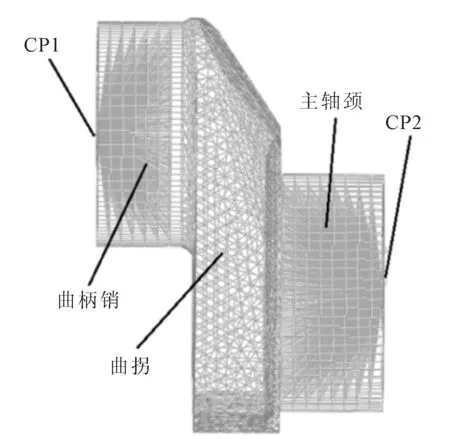
图2 曲拐的有限元模型

1.2 材料

船用柴油机曲轴的材料牌号为31CrMoV9，根据《金属材料拉伸试验标准》(GB/T 228.1—2010)对其进行单轴拉伸方法试验，根据《金属材料疲劳试验旋转弯曲方法》(GB/T 4337—2008)对其进行疲劳试验。结果：弹性模量2.11 GPa，泊松比为0.3，极限强度为900 MPa，屈服强度为690 MPa；疲劳极限为405 MPa，疲劳循环极限为2×106次，S-N曲线斜率为12。

1.3 载荷

1)简化计算载荷。根据《船舶内燃机设计》手册第二章中内燃机零部件的强度及强度计算基础，计算出气体爆压时曲轴最大受压工况以及在上止点时曲轴最大受拉工况。

经计算得出最大爆压工况曲轴承受压力为3 140 kN，最大受拉工况曲轴承受拉力为437 kN。在加载时，将耦合点CP2固定，分别在耦合点CP1处施加压力和拉力。耦合点CP1和CP2见图2。

2)协同仿真分析载荷。利用模态理论结合弹性动力润滑理论，在动力学软件VIRTUAL ENGINE中建立曲轴系统刚柔耦合模型，包括曲轴、连杆、活塞、机体等部件，主要部件见图3，以GT-POWER计算所得的缸压曲线(图4)作为输入条件，并确定点火顺序，对曲轴系统进行动力学仿真。然后，根据多体动力计算结果，提取曲柄销及主轴颈处的载荷历程。

图3 VE动力学模型

图4 缸压曲线

图5 曲柄销及主轴颈处载荷

图5为一个周期内作用在曲柄销和主轴颈处的各个力的力谱，第一通道CH1对应的是曲柄销处所受的X方向的力，其方向与爆发气体压力施加在活塞上的方向相同，其趋势也与气体爆发压力相同，在约为180°时所受为最大惯性力，在约为360°时为最大爆压力。与之相应的第6通道CH6承受与通道1相反的力。第2、3通道为主力在Y、Z方向的分解。通道4、5为所受的转矩，都接近零，与实际情况相一致。 7个通道分别对应曲柄销处X、Y、Z、CM1、CM2方向的力以及主轴颈处X、Y方向的力。其余各通道的力值为零，文中不予考虑。在有限元软件ABAQUS中计算7个通道对应的单位载荷的应力应变结果与曲柄销及主轴颈处的力谱一起作为疲劳分析的输入条件，进行疲劳分析。

2 疲劳模型

疲劳模型的创建一直是疲劳分析的重点[9]。文中曲轴的材料为31CrMoV9，其S-N曲线表达式如下。

(1)

式中：σaf,C——疲劳强度极限;

KC——曲线斜率;

Ncf,C——极限循环次数。

基于影响因子的疲劳安全系数分析，根据FKM标准，考虑到应力梯度、平均应力、加工工艺、可靠性等因素的影响，对S-N曲线的3个参数：σaf,C、Kc、Ncf,C进行修正。

首先，对于疲劳强度极限σaf,C进行修正时，考虑到交变应力极限、表面处理、几何尺寸、温度、统计影响、应力梯度、平均应力等影响因子。其次，对于曲线斜率进行修正时，考虑到交变载荷、材料参数、应力梯度、表面粗糙度(锻造)、平均应力等影响因子。最后，对极限循环次数Ncf,C进行修正时，考虑到局部S-N曲线、热机械参数、平均应力、局部S-N曲线极限疲劳强度、材料受拉力(或压力)的交变应力极限等影响因子。

根据FKM标准，选取的主要参数有：表面粗糙度RZ=3.2 μm，统计学影响90%，表面采用渗氮处理,影响数值为1.30。其余参数由软件FEMFAT根据FKM经验公式自动算出。

3 结果分析与讨论

3.1 简化计算结果

图6 应力分析结果

简化载荷进行分析时，考虑了在活塞上止点时曲轴受最大拉力工况以及在爆压力时曲轴最大受压。计算结果见图6。在惯性力工况下，如图6a)所示，可以看出曲轴有向上拉伸趋势，在曲柄销与曲柄臂相交圆角处出现最大拉应力。在爆压力工况，如图6b)所示，曲轴有被向下压缩趋势，在曲柄销与曲柄臂相连处的圆角处出现最大的压应力。经过计算得出应力幅值，见图6c)，可以看出在曲柄销与曲柄臂相连的圆角处应力幅值最大。

将有限元计算结果导入疲劳分析软件得到疲劳应力结果，见图7。图中白颜色的区域就是应力幅值变化很小的区域，从图中看出,该区域为疲劳安全系数较大的位置，这与实际情况相符。从疲劳分析结果云图中可以看出,在曲柄销和曲柄臂连接的区域是危险区域，该处疲劳安全系数较低，最小安全系数在节点480处，值为2.795 7，该点也是应力计算中应力变化最大的节点。

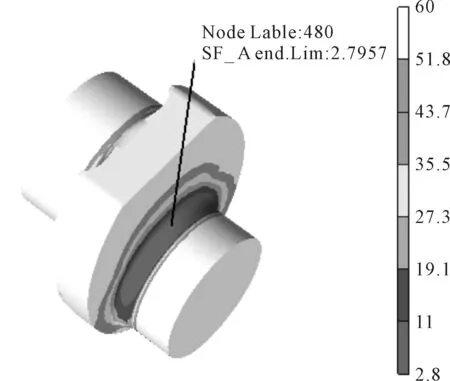
图7 简化计算疲劳安全系数结果

3.2 协同仿真分析计算

先计算出7个通道对应的单位载荷应力，作为疲劳计算的输入条件。同时将7个通道对应的载荷谱进行输入。进行线性叠加，得到曲拐的实际应力结果。再根据曲轴一个周期内的实际应力结果，作为疲劳分析的应力曲线，计算出曲轴疲劳安全系数。从图8可以看出，最危险的区域也在主轴颈、曲柄销与曲柄臂的连接圆角处。相应的在480号节点处出现最大应力幅值为144.4 MPa，最小安全系数为2.617 1。

图8 根据全载荷周期计算疲劳分析结果

4.3 结果对比分析

对比图7和图8可以清楚地看到两种不同载荷提取方案对应的疲劳安全系数的结果。由两者的结果云图可以看出，危险区域都在曲柄销、主轴颈和曲柄臂的连接圆角部分。其中最危险的区域为曲柄销和曲柄臂的内侧连接圆角。从区域的范围来看，简化的方案得到的疲劳危险区域较小，而根据全载荷周期计算疲劳结果的区域范围较大。

简化法和协同法计算出最小安全系数分别为2.795 7和2.617 2，且都是480号单元出现最小安全系数。两个结果相差6.6%。应力幅值分别为156 MPa和144.4 MPa，简化法计算出应力幅值大于协同法。可见，在设计初期使用简化法对曲轴进行疲劳安全系数的预测是可行的，在详细设计阶段可以使用协同法对疲劳性能进行研究。