绞吸挖泥船柔性钢桩缓冲系统的液压控制回路分析

,

(上海交通大学 海洋工程国家重点实验室，上海 200240)

大型绞吸挖泥船的定位桩受力复杂，在恶劣海况下将承受极大的波浪载荷，易发生断桩事故。因此，如何减小定位桩受力，保证其可靠性，以提高大型绞吸挖泥船的抗风浪能力成为当前许多学者研究的问题之一[1-2]。本文以某大型绞吸挖泥船的柔性钢桩缓冲系统为研究对象，在AMESim仿真的基础上，具体分析液压控制回路中蓄能器和阻尼阀对缓冲效果的影响，为液压控制回路的设计提供依据。

1 柔性钢桩缓冲系统工作原理

1.1 柔性钢桩缓冲系统的构成与原理

柔性钢桩缓冲系统(又称交叉钢丝绳纵向缓冲系统)是目前较为常见的绞吸船定位桩纵向缓冲系统，该系统主要由钢丝绳、导向滑轮、张紧油缸和液压控制回路组成，见图1。柔性钢桩缓冲系统对称布置在定位桩台车的左右两侧，每侧分别由2根钢丝绳、2个张紧油缸、导向滑轮以及液压控制回路组成，两侧同步控制。图1为柔性钢桩系统右侧的结构示意图。图中假定船体固定不动(张紧油缸，转动中心O点，导向滑轮H、G，钢丝绳端I、J、K、M均固定在船体上)，定位桩台车系统可绕船体纵向转动(绕O点转动)，定位桩可在台车内自由垂直滑动，两个张紧油缸的无杆腔分别连接独立作用的液压控制回路。

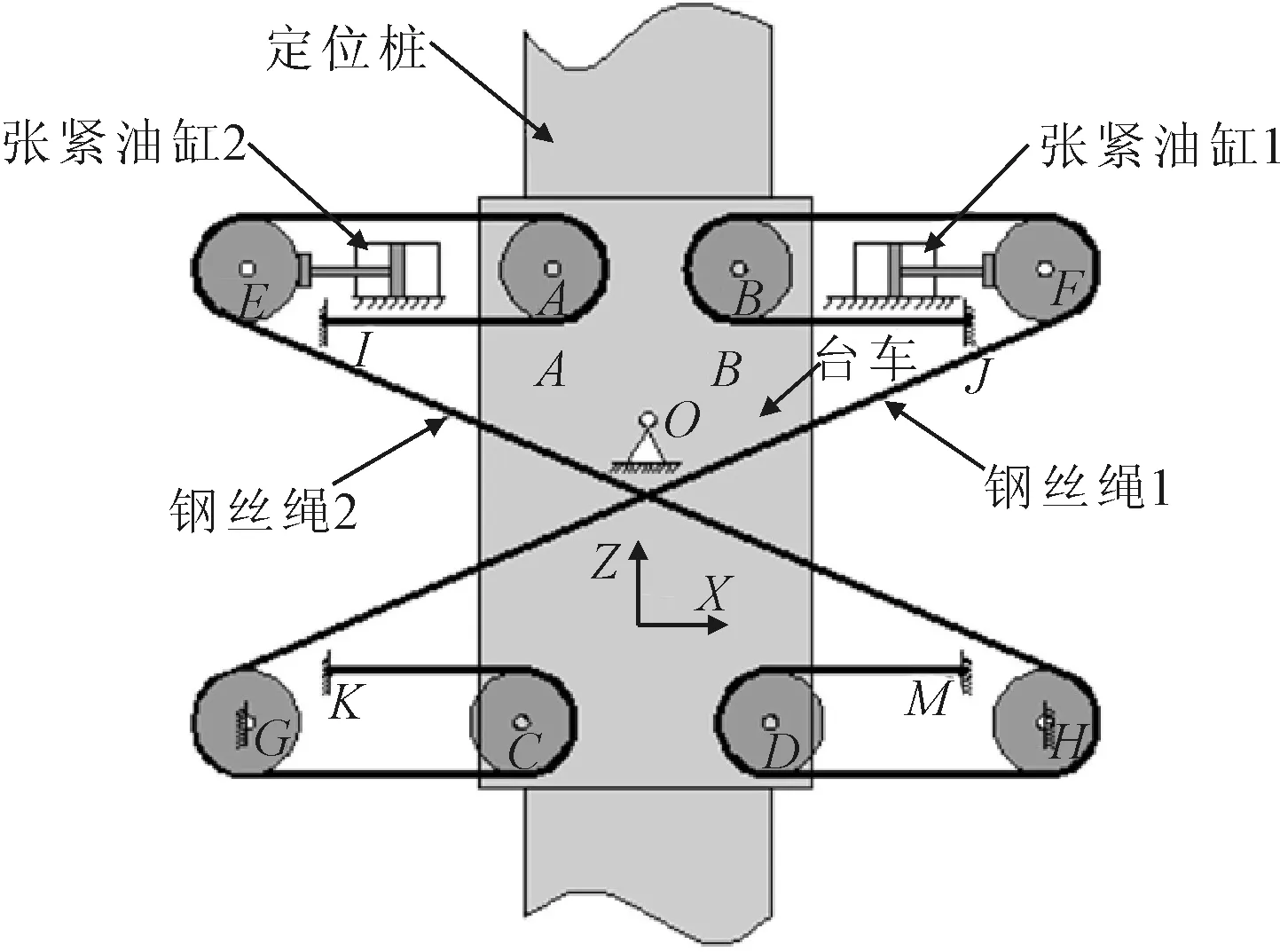
图1 柔性钢桩(右侧)系统

柔性系统工作前，液压控制系统通过张紧油缸对钢丝绳施加一定的预张力使钢丝绳张紧，两根交叉的钢丝绳分别向定位桩-台车系统施加大小相同、方向相反的弯矩，则定位桩上所受纵向弯矩为0。当绞吸船受波浪载荷作用，与定位桩发生相对转动时，交叉钢丝绳的张力发生变化，船舶运动产生的纵向弯矩通过钢丝绳缓冲系统传递给钢桩。

实际作业时，定位桩基本保持竖直，船体发生纵摇。当船体顺时针纵摇至某一倾角θ时，定位桩相对船体逆时针转动，此时，钢丝绳1伸张，张力增加，钢丝绳2收缩，张力减小，见图2。与此同时，张紧油缸1在钢丝绳及液压控制回路的共同作用下收缩，活塞内移，从而减小了钢丝绳1的伸张量和张力增加值。同理，张紧油缸2通过伸张运动减小了钢丝绳2的收缩量和张力减小值。由此可见，液压控制回路通过控制张紧油缸的活塞运动来减小钢丝绳的张力变化量，从而减小定位桩所受的纵向弯矩值，起到缓冲作用。

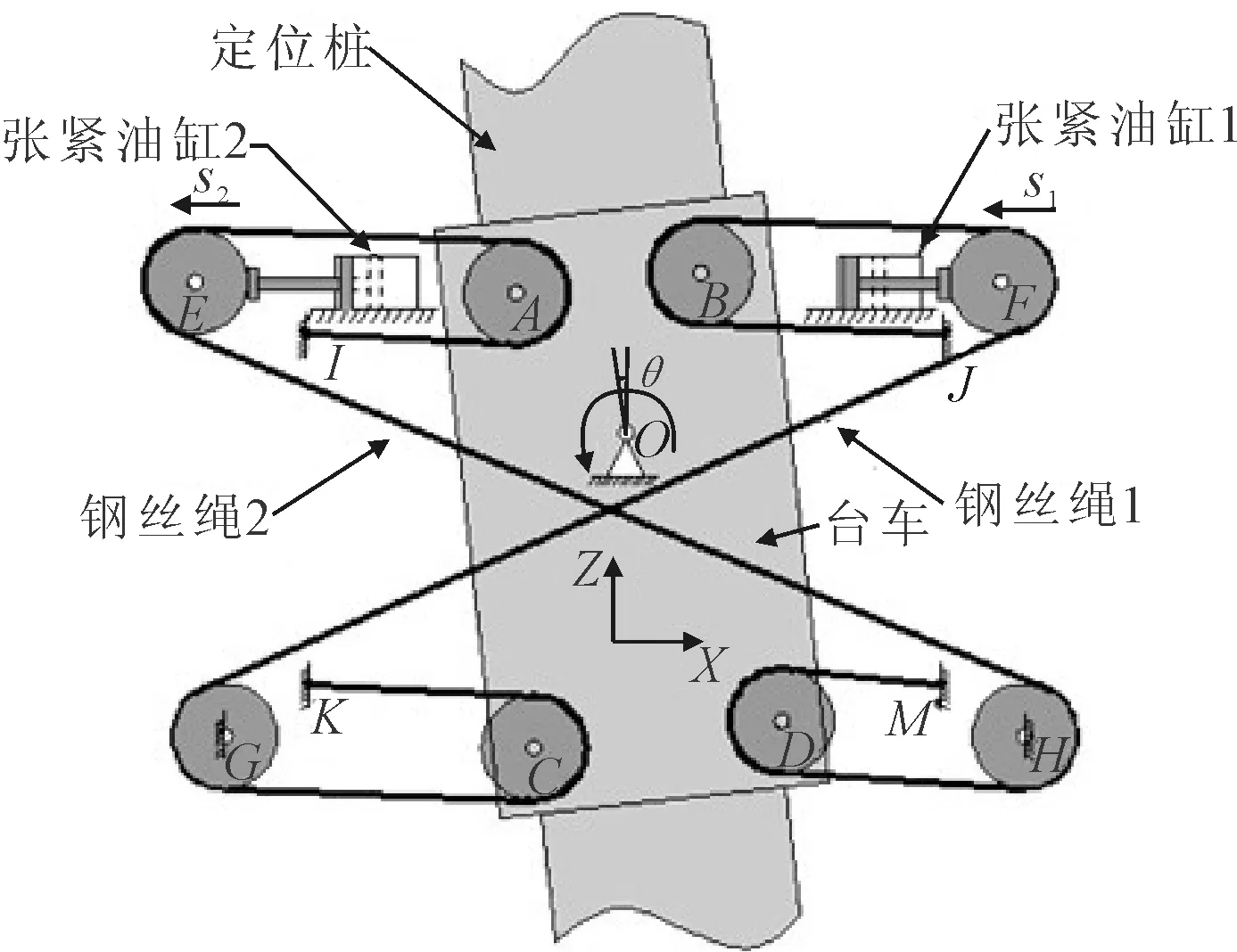
图2 定位桩相对船体旋转时的钢丝绳变化

液压控制回路对定位桩受力影响见图3。若张紧油缸无杆腔封闭，活塞固定不动，此时，船体的微幅纵摇即会在定位桩上产生较大的弯矩值；若张紧油缸根据外部力的大小变化，在液压控制回路调控下产生伸缩运动，则船体相对转动所产生的作用在钢桩上的弯矩值将大幅减小。

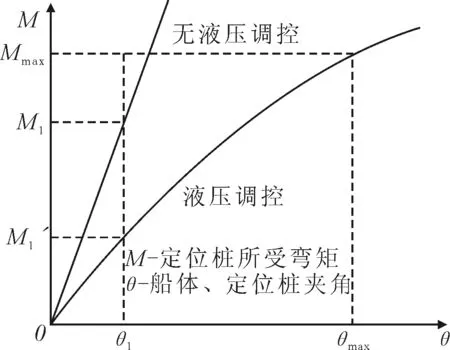
图3 定位桩特性曲线示意

液压控制回路工作时，张紧油缸的伸缩与定位桩转动同步进行，达到动态平衡。但在计算钢丝绳长度变化时，将这两个运动拆分，分别计算定位桩转动θ和张紧油缸伸缩s对钢丝绳长度的影响，见图4。

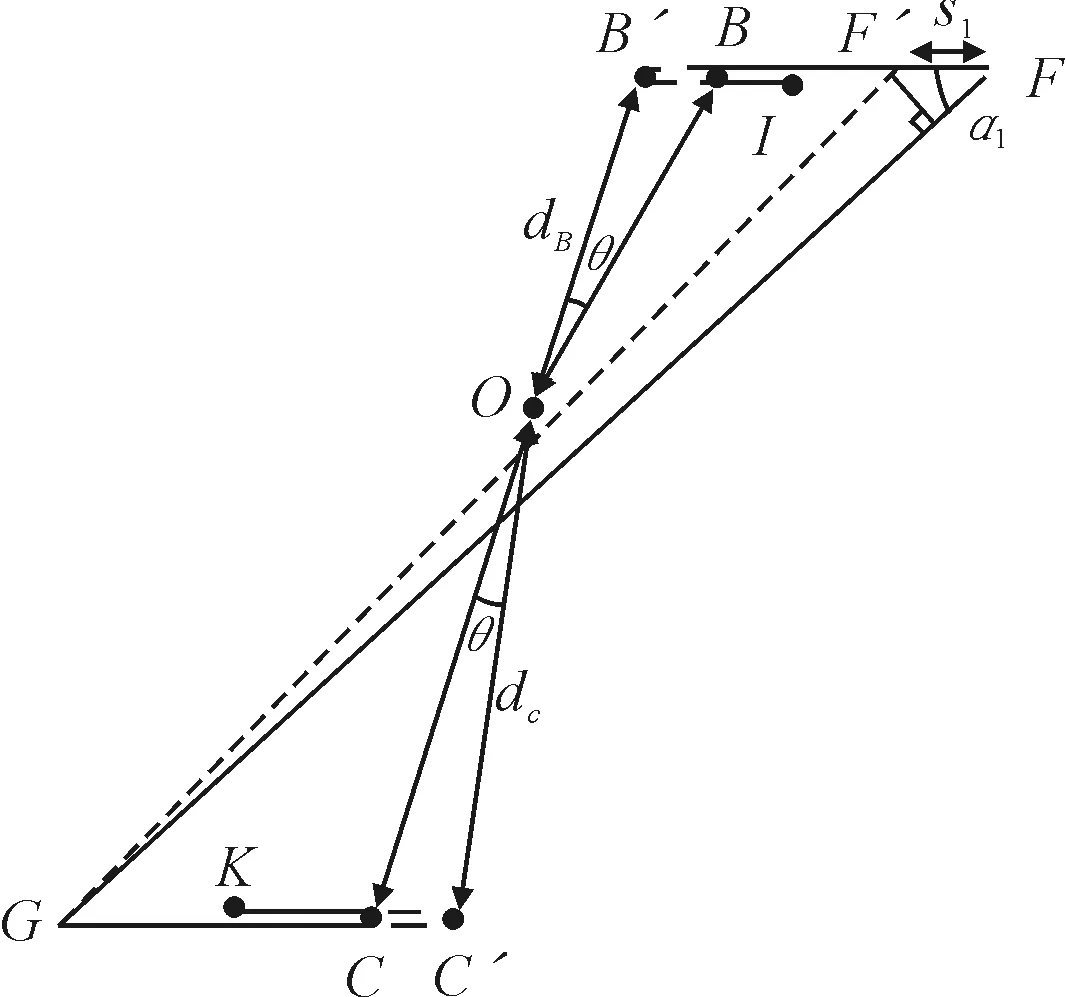
图4 钢丝绳1长度计算

图4中，粗实线为定位桩相对转动前的钢丝绳1位置；粗虚线为定位桩相对转动θ角，张紧油缸收缩s1后的钢丝绳位置。已知θ和s1相对于钢丝绳长度而言为小量，故定位桩相对转动引起的钢丝绳伸长量可近似为la=2(dB+dC)θ，张紧油缸收缩引起的钢丝绳收缩量可近似为lb=s1(1+cosα1)，即总伸长量为Δl1=2(dB+dC)θ-s1(1+cosα1)。

假设钢丝绳张力仅由其伸缩量和刚度来决定，此时钢丝绳1张力F1为

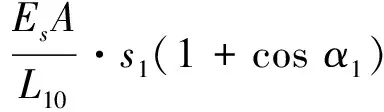
(1)

同理，钢丝绳2张力F2为

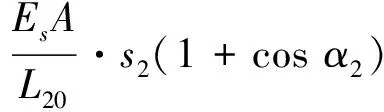
(2)

式中：Fi0——钢丝绳i的预张力;

Li0——钢丝绳i的初始长度;

Es、A——钢丝绳的弹性模量和横截面积;

dj——导向滑轮j相对于转动中心O的距离;

si——张紧油缸i的活塞位移,αi为钢丝绳i夹角(见图4)，(i=1,2;j=A,B,C,D)。

考虑到柔性钢桩缓冲系统的对称性，4根钢丝绳作用在定位桩上的弯矩M为

M=2(2F1H-2F2H)=4H(F1-F2)

(3)

式中：H——导向滑轮A、D(或B、C)之间的垂向距离。

1.2 液压控制回路功能分析

大型绞吸挖泥船柔性钢桩缓冲系统的液压控制回路主要由张紧油缸、囊式蓄能器、阻尼调节阀、溢流阀、方向控制阀、液压泵和油箱等组成，如图5所示，其回路流动状态与图2所示的定位桩相对转动相对应。

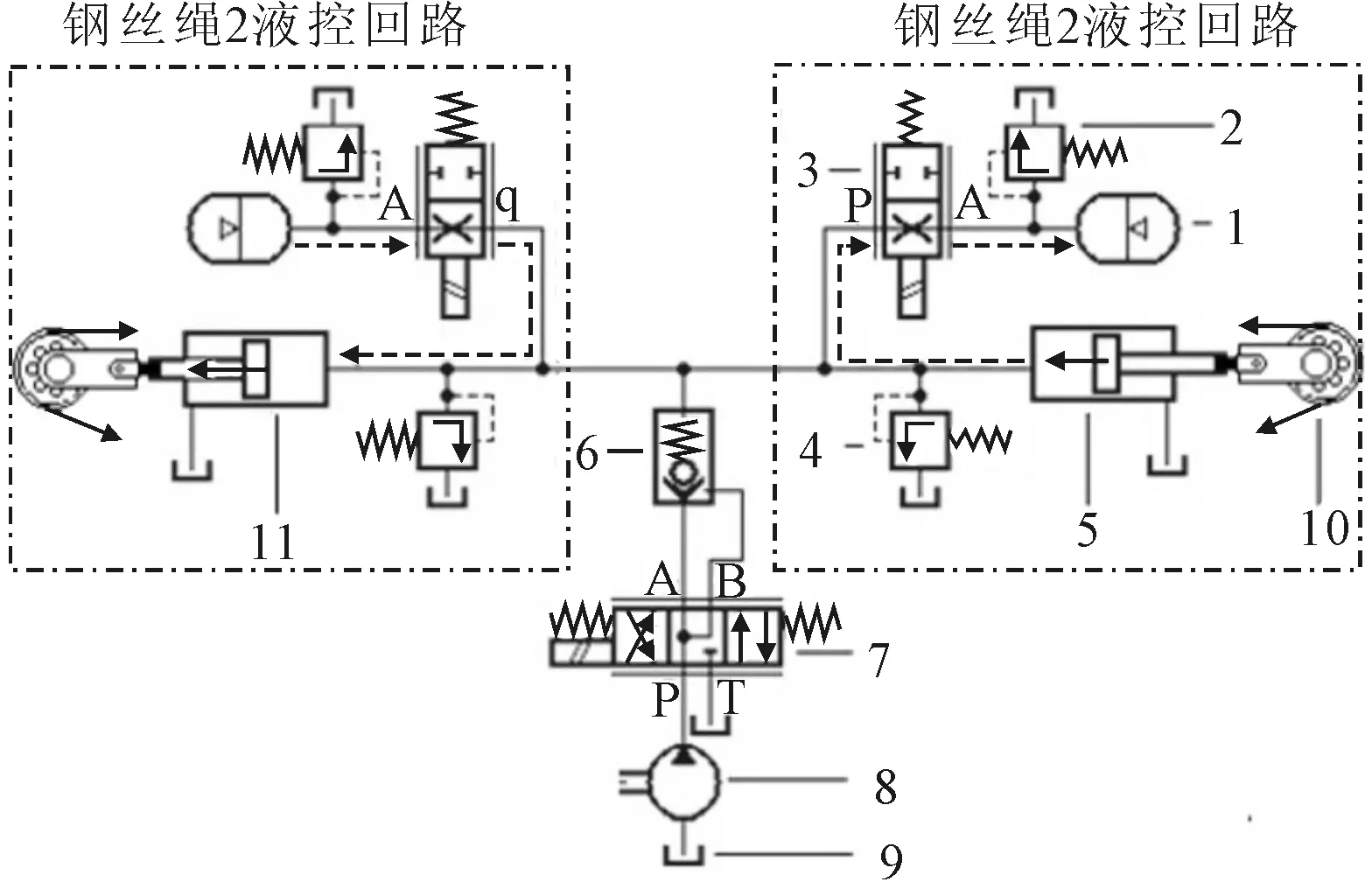
1-囊式蓄能器；2,4-溢流阀；3-二位二通换向阀(阻尼调节阀)；5,11-张紧油缸1、2；6-液控单向阀；7-三位四通换向阀；8-液压泵；9-油箱；10-导向滑轮图5 液压控制回路示意

图5中，三位四通换向阀用于改变控制回路与液压泵、油箱的连接状态，使回路处于加油、泄油或闭环工作状态。当液压控制回路工作时，三位四通换向阀7处于中位，二位二通换向阀(阻尼调节阀)连通，此时钢丝绳1、2的液控回路均处于闭环状态。当定位桩相对船体逆时针转动时，张紧油缸1活塞杆上的负载增加，油缸收缩，油液从其无杆腔流经阻尼调节阀回到蓄能器，蓄能器气囊收缩，储存能量；张紧油缸2活塞杆上的负载减小，油缸伸张，油液从蓄能器流经阻尼调节阀至油缸无杆腔，蓄能器气囊膨胀，释放能量。由于波浪载荷随时间变化，张紧油缸活塞杆上的负载也随时间变化，但液控回路通过调节其无杆腔的油液压力，限制了油缸活塞的运动速度和幅值，从而减缓了作用在定位桩上的波浪载荷。

此外，当闭环中的二位二通换向阀处于断开状态时，张紧油缸活塞固定不动。在这种状态下，定位桩和船体只能通过钢丝绳本身的伸缩发生极小的相对转动。这种工况主要在平静海况或内河使用，此时船体传递给定位桩的波浪弯矩不大，不需要缓冲，绞吸船作业的关键是提高船体定位精度和生产效率。

2 闭环回路数学模型

如图5所示，除用来过载保护的溢流阀外，闭环回路主要由张紧油缸、囊式蓄能器和阻尼调节阀(二位二通换向阀)组成。

囊式蓄能器是储能、放能装置。工作时，气囊中的气体状态变化遵守玻意耳定律[3]，即

(4)

式中:p0、V0——蓄能器充液前的充气压力和气囊容积，此时气囊充满壳体内腔；

pt、Vt——蓄能器最任意时刻的工作压力和气囊体积；

n——与气体变化过程相关的多变指数，对于绝热过程，n=1.4。

对式(4)两边求导，可得蓄能器气囊体积变化和压力变化的关系

(5)

已知蓄能器气囊体积的总变化量和张紧油缸无杆腔的体积变化量Ap·s相同，其中，Ap为张紧油缸活塞面积，s为活塞移动位移；而气囊压力与钢丝绳张力动态平衡。

若只有1个蓄能器，则活塞移动s引起的蓄能器压力变化为(-npt/Vt)APs；若有N(N≥2)个蓄能器并联，则活塞移动s引起的蓄能器压力变化量变小，为1/N·(-npt/Vt)APs。与此同时，钢丝绳张力的变化也变缓。由此可知，缓冲系统工作能力与蓄能器数量有关。

阻尼调节阀是液压控制回路的关键元件，它通过节流孔的作用，使蓄能器和张紧油缸的油液压力发生压力差，从而对张紧油缸上的负载产生阻尼力，减小了张紧油缸活塞运动的速度和位移。阻尼调节阀的形式多样，本文研究的绞吸挖泥船钢桩缓冲系统的阻尼调节阀由插装阀、或门型梭阀、二位三通阀共同组成，见图6。

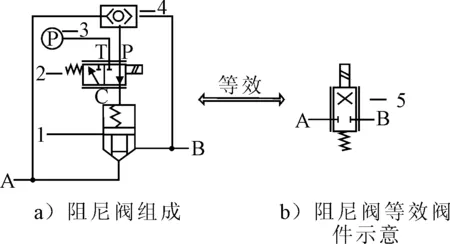
1-二通插装阀;2-二位三通换向阀;3-压力源;4-或门型梭阀;5-二位二通换向阀

该阻尼调节阀的工作状态取决于插装阀的规格参数及阀芯位移。已知插装阀阀芯上的作用力如图7所示。

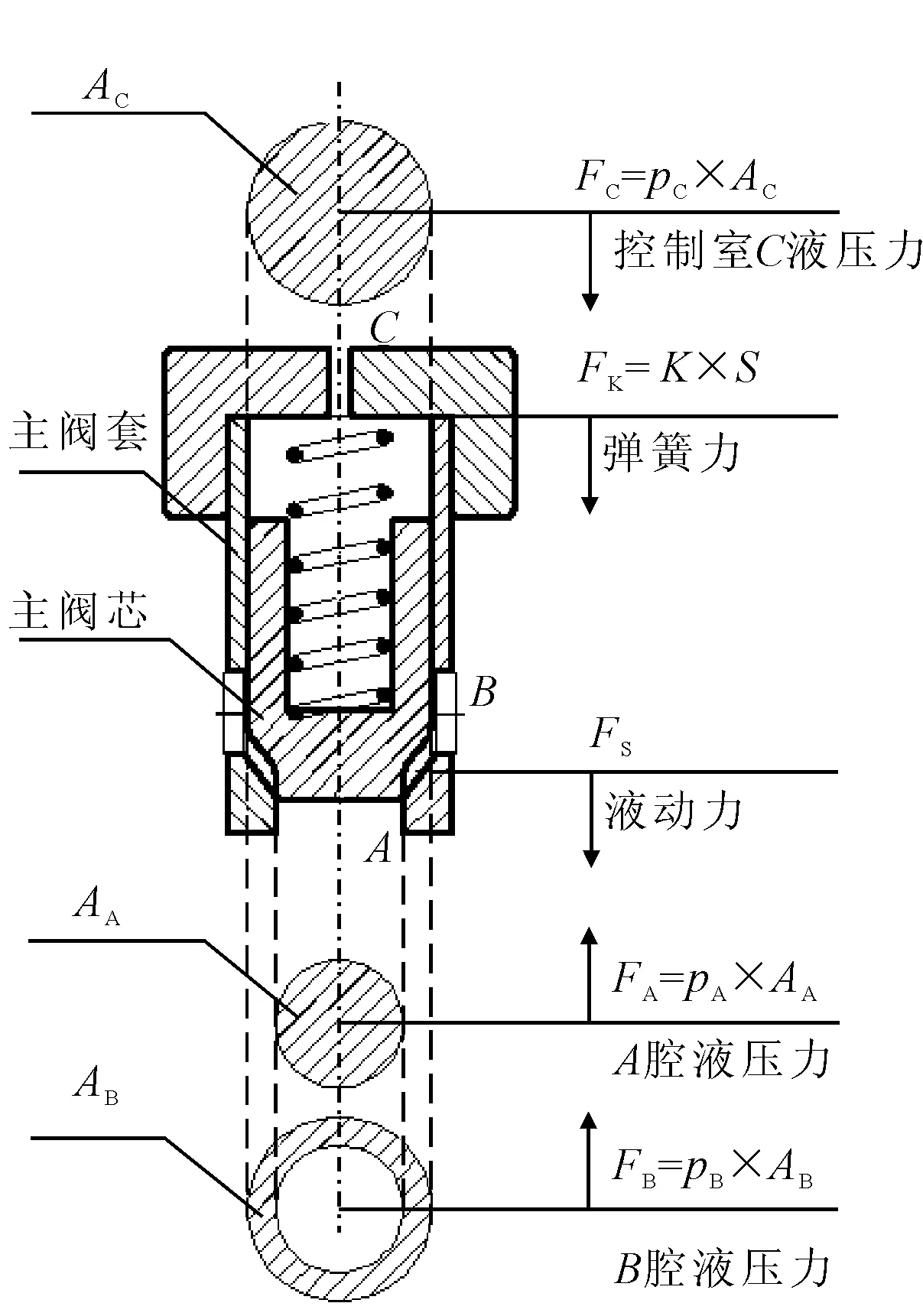
图7 插装阀阀芯受力分析

当合力∑F=pBAB+pAAA-pCAC-FK-FS>0时，插装阀开启；反之，则阀芯关闭。当控制室C的压力由A、B口的高压力端控制时(A、B口通过或门型梭阀与C相连)，由AC=AA+AB可知，∑F<0，插装阀始终保持关闭。当回路中的A、B口的压力克服弹簧初始压力FK、由流体流量变化引起的附加液动力FS，以及控制油路C压力时，插装阀开启。若控制油路C的压力极小，则阀芯开度主要受pA,pB,弹簧刚度k,及流量变化的影响，即

x=f(pA,pB,k,Q)，pC→0

(6)

假设阀芯位移为x，如图8所示。

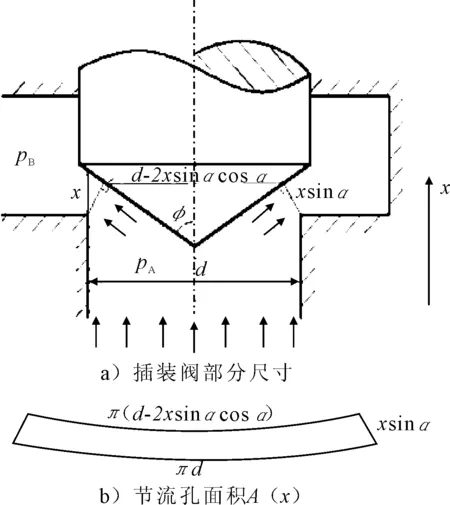
图8 插装阀节流孔尺寸及面积计算

此时的节流口面积为一圆台侧面积。

(7)

式中:d——阻尼孔(A口)孔径;

φ——阀芯半锥角。

已知插装阀节流口满足孔长小于孔径的一半，属于薄壁小孔[4]，故插装阀的阻尼力(即A、B口压差)与流量Q[5]的关系可按下式计算

即

(8)

式中:Cd——流量系数，与流体粘性有关；

A(x)——节流口面积；

ρ——流体密度。

结合式(6)、(7)、(8)可知，阻尼阀的阻尼力与流体流量和节流孔面积有关，而节流孔面积受弹簧刚度k、阻尼孔(A口)孔径d、阀芯半锥角φ影响。

故本文仿真主要考察以上3个参数，以及蓄能器数量对缓冲效率的影响。

3 闭环回路AMESim仿真

3.1 仿真模型

AMESim软件为多学科领域复杂系统建模仿真平台，包括有机械、信号控制、液压、液压元件设计(HCD)等工程学科的应用库。本文在此基础上仿真了液压控制回路处于闭环工作状态时的情况，见图9。仿真模型中的模块参数见表1。

1-张紧油缸有杆腔；2-位移感应器；3-张紧油缸活塞质量模块；4-张紧油缸无杆腔；5-可变容积模块；6-插装阀阀芯插件；7-插装阀阀芯质量模块；8-插装阀弹簧腔；9,13-函数信号；10-载荷(力)输入信号；11-信号汇总；12-常数信号；14-三角函数信号

图9液压控制回路闭环工作状态示意

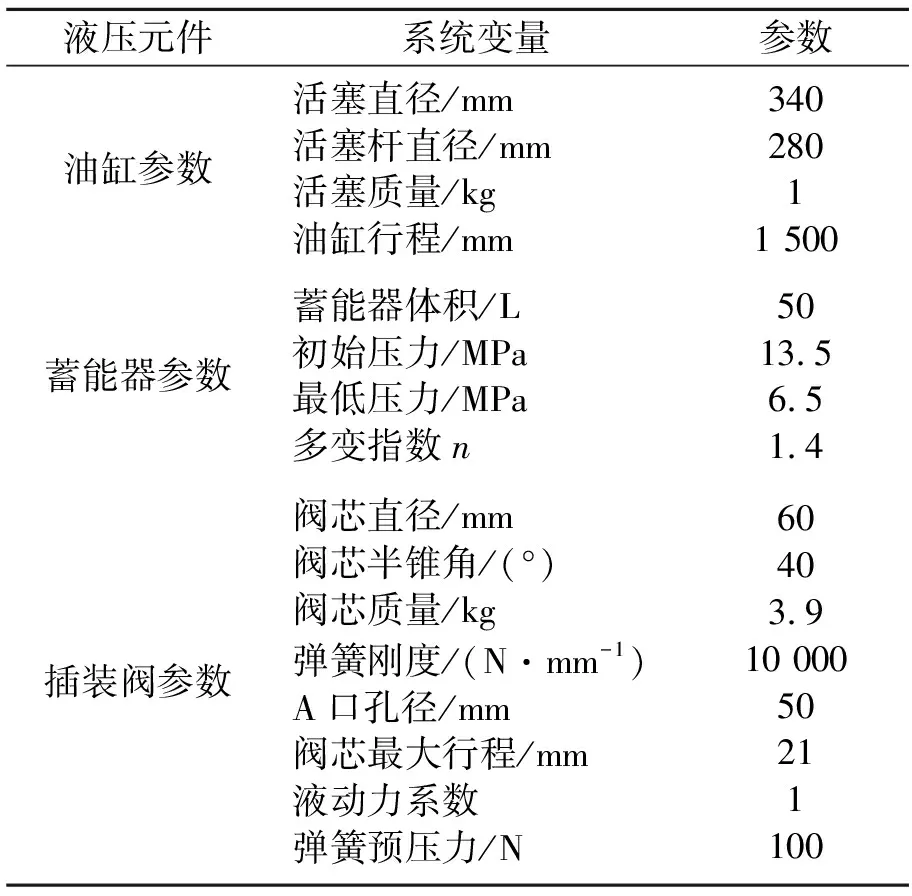
表1 仿真模块参数

在考虑张紧油缸活塞杆所受的外载荷时，本文假设挖泥船船体在作业海况(波高1.5 m，波周期6 s)下的纵摇运动为不衰减的正弦运动，该运动引起的柔性钢桩钢丝绳张力变化，以及张紧油缸位移对钢丝绳张力的影响可由式(1)、(2)得到，在仿真系统中可用9～14的信号模块来模拟。其中信号12对应公式中的第1项，为钢丝绳初始张力；信号13对应公式中的第二项，为由定位桩转动引起的钢丝绳张力变化，其输入端信号14为船体纵摇角的正弦变化；信号9对应式中第3项，为油缸活塞运动引起的钢丝绳张力变化。该反馈系统涉及到的钢丝绳参数及船体纵摇运动参数见表2。

表2 反馈系统参数

3.2 数值仿真结果

绞吸船在设计工况(波高1.5 m，周期6 s)下所受的弯矩M0=3.63×107Nm。若无缓冲系统，该弯矩将全部传递至定位桩上。不妨定义柔性钢桩的缓冲效率η：

(9)

式中：Mmax——缓冲后定位桩弯矩的最大值。

改变蓄能器数量，插装阀的弹簧刚度k、阻尼孔(A口)孔径d和阀芯半锥角φ，即可得到不同条件下作用在钢桩上的弯矩时域变化曲线，见图10～17。

图10、11表明，随着随蓄能器数量的增加，缓冲后的定位桩最大弯矩减小，缓冲效率增大；缓冲前后的定位桩弯矩周期不变，相位差随蓄能器数量的增加而增大。当蓄能器数量在4～19之间变化时，缓冲效率为7.7%～16.7%，定位桩弯矩的差值可达3.27×106Nm，缓冲前后的弯矩相位差为35°～40°。

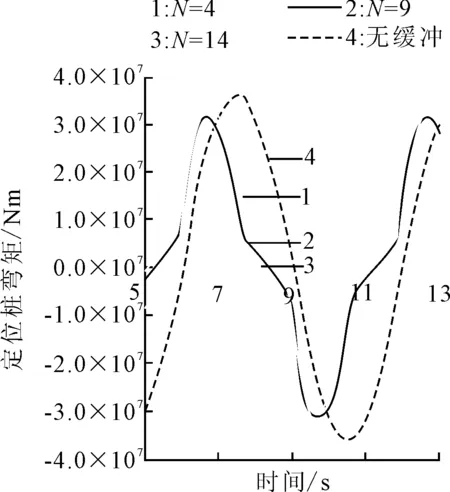
图10 不同蓄能器数量N下的弯矩时域曲线

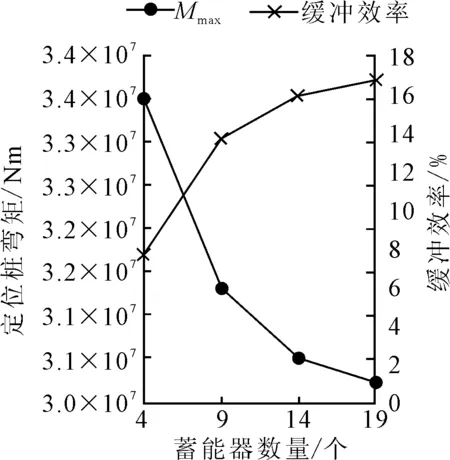
图11 蓄能器数量N对缓冲效率的影响

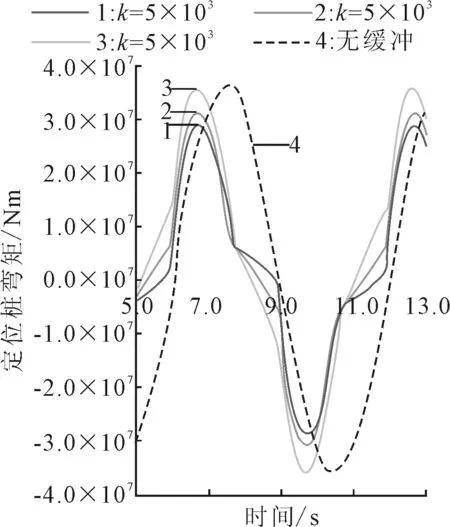
图12 不同弹簧刚度k下的弯矩时域曲线

图13 弹簧刚度k对缓冲效率的影响

图12、13表明，随着弹簧刚度k的增加，缓冲后的定位桩弯矩增大，缓冲效率减小；缓冲前后的定位桩弯矩周期不变，弹簧刚度对两者相位差的影响很小。当阻尼阀弹簧刚度在5 000～15 000 N/mm之间变化时，缓冲效率为2.1%～21.8%，定位桩弯矩的差值可达7.14×106Nm。

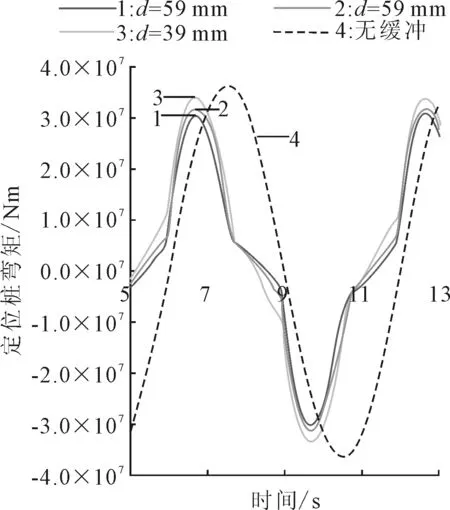
图14 不同阻尼孔直径d下的弯矩时域曲线

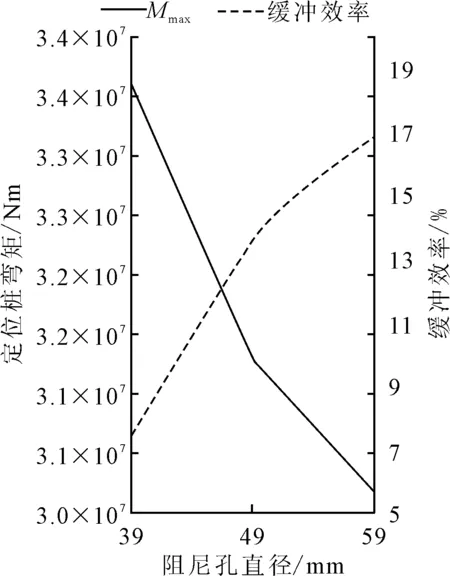
图15 阻尼孔直径d对缓冲效率的影响

图14、15表明，随阻尼孔直径d的增加，缓冲后的定位桩弯矩减小，缓冲效率增加；缓冲前后的定位桩弯矩周期不变，阻尼孔直径对两者相位差的影响很小。当阻尼孔孔径在39～59 mm之间变化时，缓冲效率为7.4%～16.9%，定位桩弯矩的差值可达3.43×106Nm。

图16、17表明，随着阀芯半锥角φ的增加，缓冲后的定位桩弯矩减小，缓冲效率增加；缓冲前后的定位桩弯矩周期不变，阀芯半锥角φ对两者相位差的影响很小。当阀芯半锥角在30°～50°之间变化时，缓冲效率为7.8%～16.9%，定位桩弯矩的差值可达3.30×106N·m。

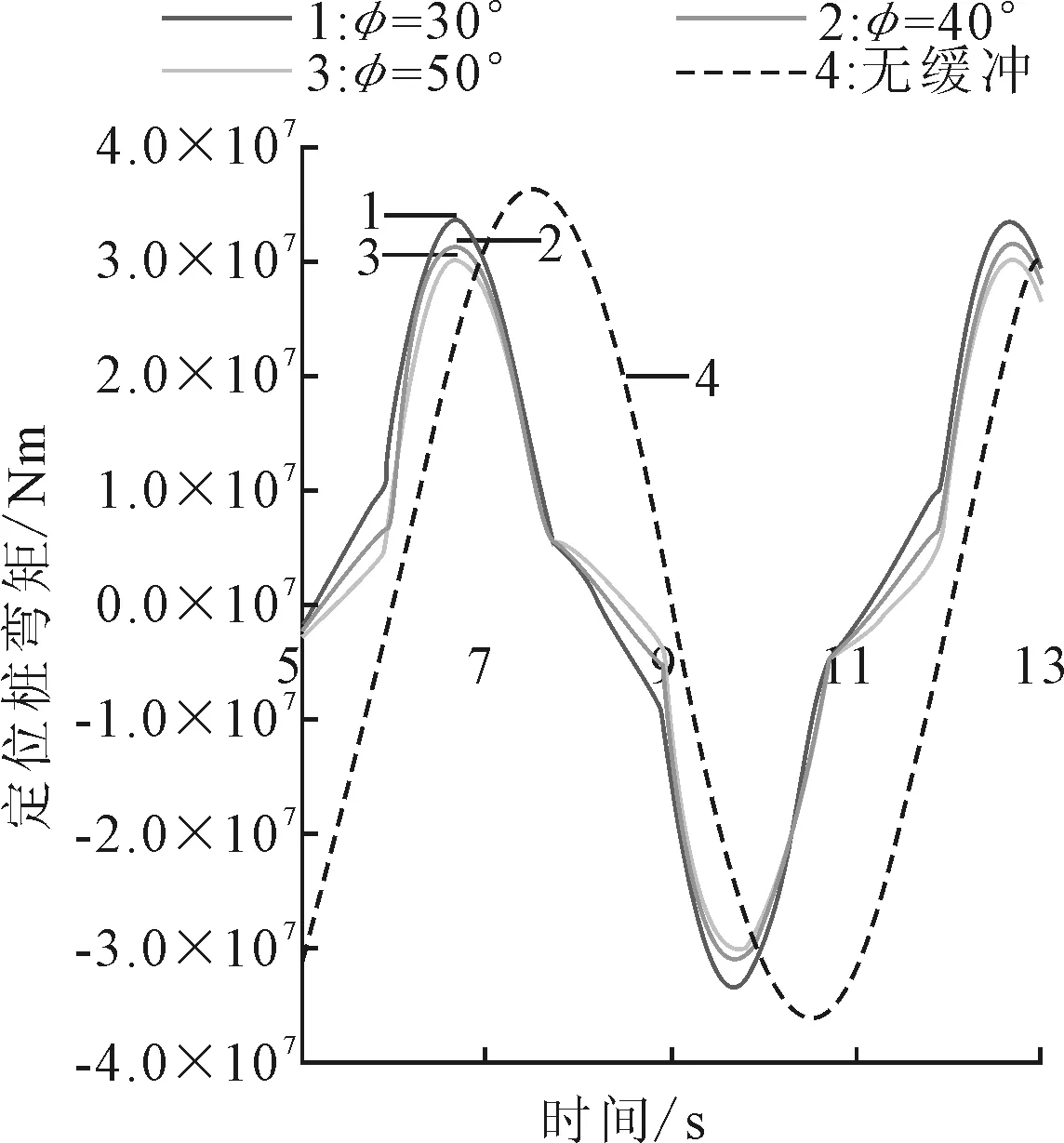
图16 不同阀芯半锥角φ下的弯矩时域曲线

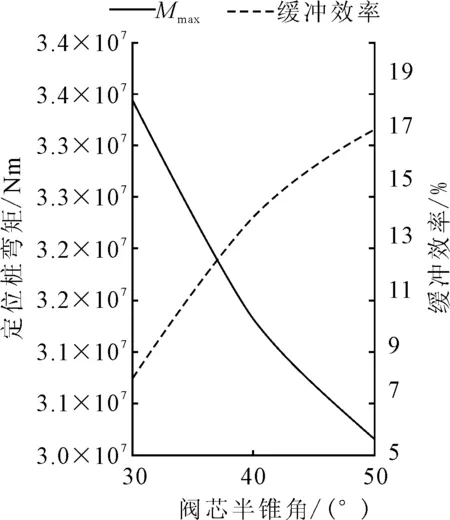
图17 阀芯半锥角φ对缓冲效率的影响

3 结论

1)柔性钢桩缓冲系统是提高绞吸挖泥船抗风浪能力的有效机构，它能减小定位桩所受的纵向波浪弯矩的峰值，并改变缓冲前后波浪弯矩的相位差。

2)蓄能器数量越多，弹簧刚度k越小，阻尼孔孔径d越大，阀芯半锥角φ越大，缓冲后的最大定位桩弯矩值就越小，缓冲效率随之增加。其中，缓冲效率受弹簧刚度的影响最明显。但在设计时，缓冲效率不应太大，否则会减小柔性钢桩缓冲系统的承载能力，当外界载荷较大时，钢丝绳发生松弛，从而引起系统失效。此外，缓冲前后的定位桩弯矩周期不变，两者相位差主要受蓄能器数量影响，蓄能器数量越大，相位差越大。这一规律可为缓冲系统设计提供依据。

3)本文在计算时假设绞吸挖泥船在作业海况下的船舶纵摇运动为不衰减的正弦运动，忽略了缓冲系统对船体纵摇运动的影响，后续研究应考虑缓冲系统和船体运动的耦合作用。

[1] Etienne Clymans, Willebroek(BE). Apparatus with flexibility mounted spud carriage: US,7900381B2[P]. 2011-03-08.

[2] 黄 贤,何炎平,蒋如宏,等.挖泥船定位桩台车系统的构成和功能[J].中国港湾建设,2008(8):67-71.

[3] 贺利乐.液压与液力传动[M].北京：国防工业出版社,2011.

[4] 顾宏伎,杨波,潘嘉明.节流孔类型对换挡缓冲时间的影响[J].机床与液压,2009,37(5):90-91.

[5] 郑淑娟,权 龙.基于CFD的液压锥阀阀芯启闭过程的液动力分析[J].机电产品开发与创新,2007,20(3):81-82.

[6] 吴沂隆.钢丝绳弹性模量的研究[J].福建林业科技,2003，30(9):62-64.