船舶耐波性试验测量数据处理系统开发及应用
2014-06-27,,
, ,
(海军驻沪东中华(集团)军事代表室,上海 200120;海军工程大学 舰船工程系,武汉 430033)
船舶耐波性试验是获得船体运动特性及流体动力性能的重要手段,包括模型试验及实船试验。模型试验常用来验证理论模型及对实船耐波性能指标的预报,常需要测量船模在规则波或不规则波中的运动响应、波浪作用力及船体运动时在流场的兴波等;实船试验则主要测量一定海况下船体的运动响应特性。获得可靠的耐波性试验数据是耐波性试验的前提,但耐波性试验测量的信号中往往包含高频的背景噪声。在实船测量时,船上的各种机械设备产生振动噪声和测量仪器中的交流电噪声是高频噪声的主要来源;船模试验时高频噪声主要来源于测量设备中的交流电噪声和拖车及其旋转机械的振动噪声。所谓趋势项是指测试信号中周期大于记录长度的成分[1]。直接对含有高频噪声和趋势项的信号进行耐波性分析会影响其精度和准确性。因此为获得可靠的试验数据,必须对这些测量信号进行滤波处理。另一方面,船舶耐波性能指标多,且船舶在波浪中航行时工况多,因此实测数据通道多,数据量大。所以开发实时可靠的船舶耐波性试验数据处理系统具有工程应用意义。
针对舰船耐波性实测信号中趋势项难以消除而影响滤波精度这一问题,文献[2]采用经验模态分解方法消除趋势项的影响。根据舰船对波浪运动响应的低频特点,在经验模态分解前先进行低通滤波,可使实测运动信号中的谱峰频率处在相对高频位置,减少EMD迭代次数,并使有用信息包含在第一个IMF中,方便对有用模态的识别。这一方法提高了分析精度,且使得实时分析成为可能。文献[3]以FFT-FS频谱细化技术来辅助分析多工况及耐波性系列试验时频谱特性,有效地用于船模耐波性试验测量数据的定量分析。本文以这两种算法为基础编制船舶耐波性试验数据的处理及分析系统,并通过实例分析说明该系统的可靠性。
1 信号处理方法
1.1 滤波方法
耐波性实测数据的处理常采用低通滤波的方法[4],其步骤是对实测时间序列去直流、快速傅立叶变换(FFT)、高频截断、反傅里叶变换(IFFT)以得到过滤高频噪声的时间序列,该方法能够过滤高频噪声,但难以过滤趋势项及低频噪声。船模对波浪运动响应是低频的,使得低频的趋势项和运动响应信号可能耦合在一起,故采用一般的滤波器难以对频率选取较准确的下限阈值。针对该问题,采用低通滤波过滤高频噪声和经验模态分解(empirical mode decomposition,EMD)消除趋势项及低频噪声影响的方法对信号进行滤波处理以提高分析精度。
EMD方法由美国人Huang于1998年提出,该方法基于信号的局部特征时间尺度,把信号分解为若干个固有模态函数(intrinsic mode function,IMF)及剩余项之和[5],这些IMF及剩余项对应的频率由高频向低频排列,每个IMF代表信号中某个频率或频段内的波动分量,突出了数据的局部特征,对其进行分析可以更准确有效地把握原数据的特征信息,而剩余项则为频率为零的项,即趋势项。该方法的一个缺点是迭代时间长。基于以上分析,本文先对实测信号进行低通滤波处理,使得有用信号处在所得信号的相对高频位置,然后采用EMD进行模态分解,相对高频的有用信号往往对应第一个IMF,而其它IMF及剩余项则为低频噪声,提取第一个IMF作为有用信号就消除了低频趋势项及低频噪声的影响。该方法处理流程见图1。该方法能够兼顾低通滤波及EMD的优点,减少EMD进行IMF分解的迭代次数并提高分析效率,同时还便于对有用模态的自动识别。

图1 实测信号的滤波处理流程
1.2 FFT-FS细化谱分析
FFT-FS实际上是一种联合采用快速傅里叶变换(FFT)及傅里叶级数展开(FS)的信号处理方法。其原理是在不增加数据长度N的前提下对信号先进行N1点FFT,初步确定信号的频幅特性,然后对FFT的离散频率通过变量代换获得连续频率,并对感兴趣的局部频段进行傅里叶级数展开获得连续的频谱曲线。关于频率的变量代换、FFT-FS、FFT更详的介绍可参考文献[6]。对于实测耐波性信号来说,感兴趣的频段是遭遇圆频率ωf附近的局部频段,因此只需对遭遇频率附近的频幅特性进行分析,从而提高分析效率及频率分辨率。
2 试验数据处理系统的开发
近年来,随着计算机多核技术及集群技术的快速发展,并行程序设计成为提高数值计算效率的主流技术之一,在Matlab2009之后,MathWorks将并行计算技术植入Matlab中,进一步加强了该软件的数值运算功能[7]。
为提高数据处理的精度及效率,基于Matlab平台,以低通滤波及EMD方法为内核,以FFT-FS细化谱分析技术作为辅助工具,开发了船舶性能试验数据处理系统,其主界面见图2。
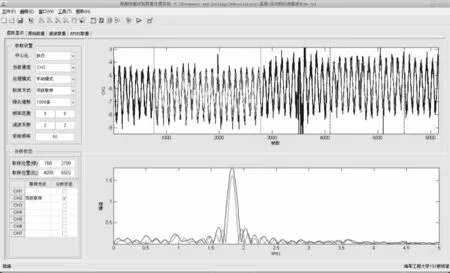
图2 程序主界面
该程序能够对耐波性试验测量数据进行滤波处理及细化谱分析,可以帮助了解实测信号的时域及频域特征,能对分析后的数据进行统计分析,如对不规则中船舶的运动响应测量信号而言,可统计其平均周期、平均值、平均幅值、最大幅值、最小幅值、三一幅值、波峰数、波谷数等重要信息。
2.1 软件介绍
该程序包含菜单栏、工具栏、图形显示及数据显示四大模块。其中菜单栏包括文件菜单、编辑菜单、工具菜单、窗口菜单及帮助文件菜单,图形显示窗口主要用于通道数据的显示、滤波结果的显示及FFT-FS细化谱的显示;工具栏包括文件格式的定义、导入及导出、图形的缩放、拖放等操作按钮;数据显示工具包括原始数据、滤波数据及细化谱数据的显示按钮。
2.2 软件使用
1)导入数据。在导入数据前对实测数据的存取格式及文件类型进行定义。为提高系统的通用性,数据结构可为单通道数据,也可为多通道数据,读取文件类型则可根据采集系统存取的数据类型进行定义。
2)数据取样。为方便对有效数据的取样,系统设置了数据取样功能,在时历曲线上按右键并在有效数据区域进行拖放则可对实测数据进行取样,见图3。
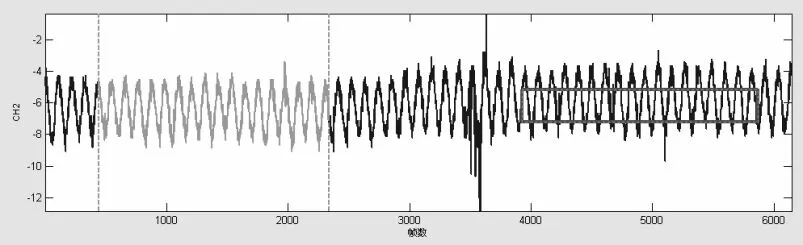
图3 数据取样
试验过程中为提高试验效率,常需要在一次试验测量中进行多个工况的测量,如规则波模型试验中常在入射波波长为短波时进行多个速度的拖曳,为提高分析效率并对试验工况测量参量进行比较,系统设置了多段取样及多段分析模式,见图4。
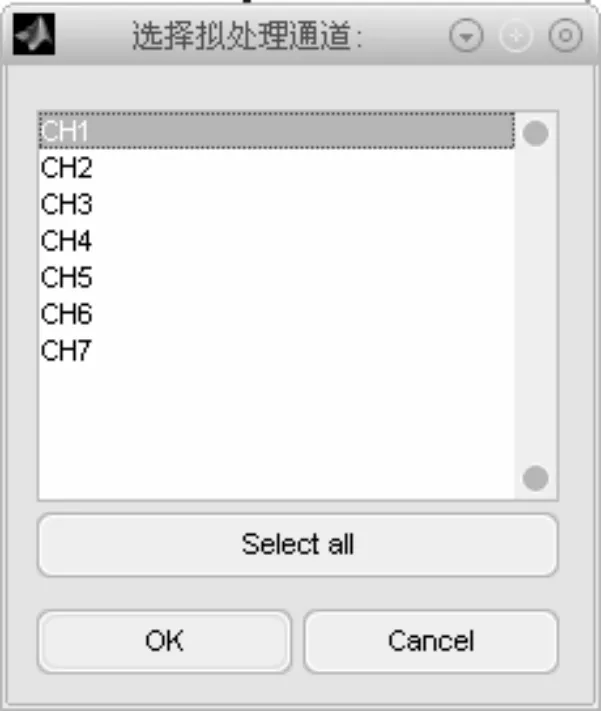
图4 通道选择
3)参数设置。包括执行中心化选项、通道选择、滤波系数设置、处理模式、取样方式、细化谱谱线数目设置及细化频段设置,见图5。
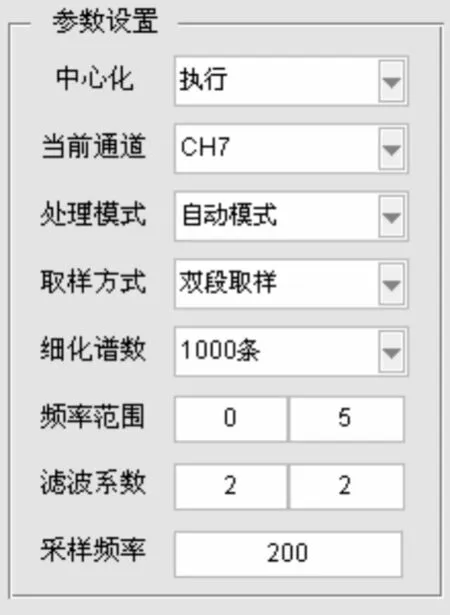
图5 参数设置
中心化选项决定对实测数据是否移除零阶量,对于非定常量,当需要提取信号的波动信息时(如运动响应信号的一阶量),需要执行中心化,对于一些定常量,如分析波浪中船体的阻力增值数据时,需要提取的是实测信号中的定常部分,不需要进行中心化。滤波系数一般默认为2,该系数为低通滤波的最小截断频率与有用信号的主频(如规则波中船模振荡的遭遇频率)的比值。细化谱线数及细化频段是进行FFT-FS细化谱分析时的输入参数,其中细化频段对应于FFT-FS分析的上、下限频率,细化谱线数为该频段内谱的离散次数,可反映信号在频域内的分辨率。处理模式包括自动模式及手动模式,手动模式为单通道信号处理模式,在信号异常时采用该方式并结合滤波系数调节滤波的质量,自动模式为多通道数据的批处理模式,当选择好待处理的通道后,系统会自动对各通道信号进行处理。
4)数据处理。参数设置好后,点击工具栏中的按钮,以执行分析。系统根据取样位置及分析模式进行滤波分析及FFT-FS分析,当分析模式为手动模式时仅对当前通道进行数据处理,当取样分析模式为自动模式时,系统对选定的每一通道进行处理,并逐一显示各通道分析结果。分析结束后,状态表格中对应通道的取样方式中会标明取样状态,分析状态中的方框会标出执行分析的状态;各通道的FFT-FS幅值谱会保存在FFT-FS数据表中(见图6),表中还给出了关于幅值谱的特征量;滤波数据表中保存了执行滤波分析通道的滤波时历数据,及对各时历数据的特征统计值(见图7)。各通道的处理结果及时历曲线通过输出菜单保存在Excel表格中。
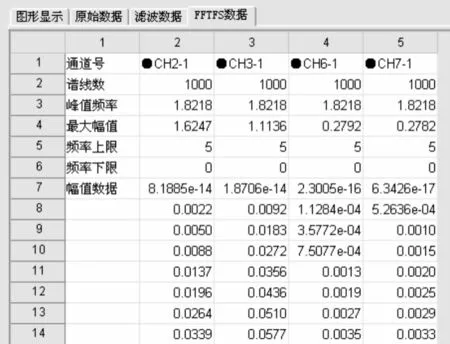
图6 FFT-FS频幅特征及细化谱
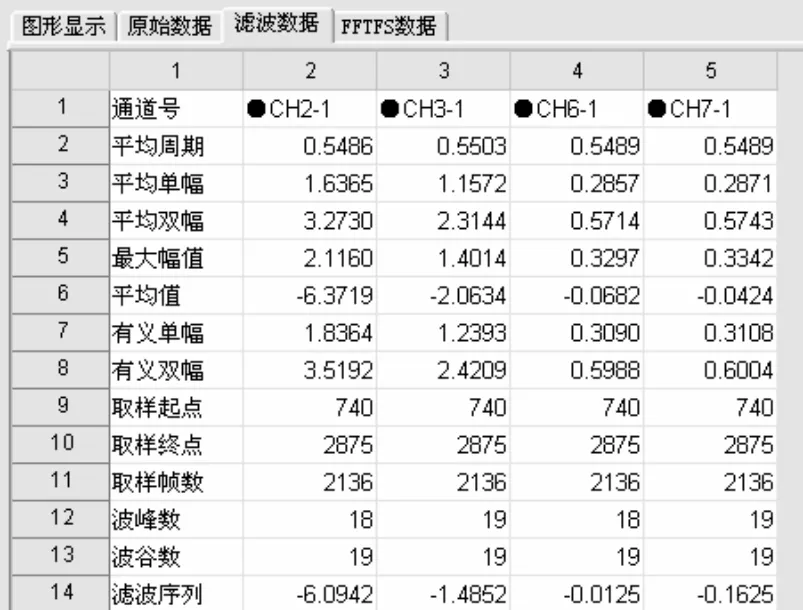
图7 滤波统计结果及时历过程记录
3 信号处理实例分析
图8给出了某船模在规则波中的垂荡运动测量数据及采用本系统分析所得的滤波曲线,图中还给出了仅低通滤波的结果。模型重173 kg,水线长3.651 m,型宽0.462 m,设计吃水0.156 m,模型速度1.021 m/s,入射波波长3 m,顶浪航行。试验模型的具体参数及试验情况参见文献[8]。
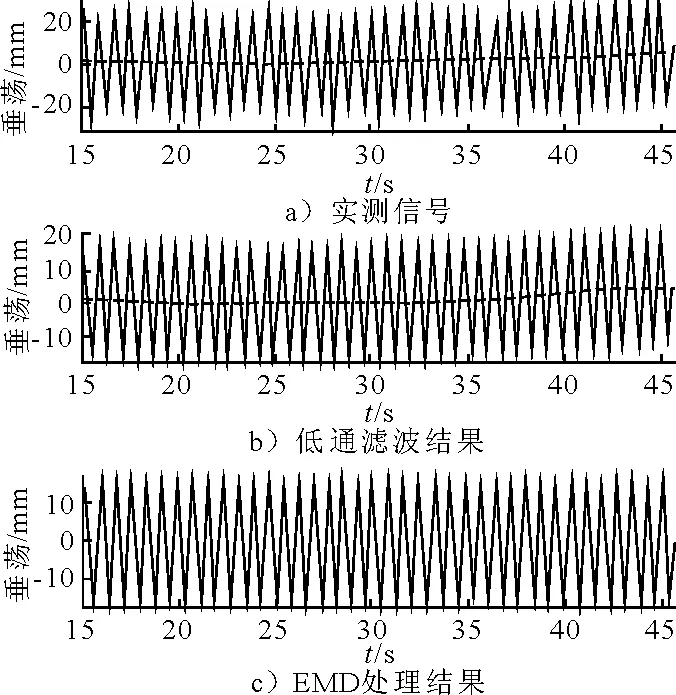
图8 实测垂荡信号及滤波结果
由图8可见低通滤波过滤了高频噪声,但未过滤趋势项的影响,而本文的滤波方法不仅消除了高频噪声的影响,也消除了低频趋势项的影响。
图9a)给出了对低通滤波所得信号进行经验模态分解所得各IMF及余量的时历曲线,图9b)给出了图8各时历曲线的FFT-FS幅值细化谱。
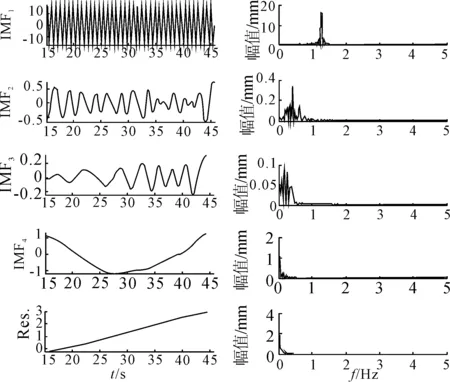
图9 低通滤波后的信号经EMD分解得到的各模态及对应的FFT-FS幅值谱
从图9可见第一个IMF确实是所需要提取的垂荡信号,且该模态对应的频率处在各模态的相对高频处。表1给出了3条时历曲线统计的平均周期、平均幅值、最大幅值、波峰及波谷数,从表1可见,未进行滤波处理的统计结果和滤波后的统计结果具有较大的差异,因此为确保分析精度,对测量信号进行滤波处理是必要的。
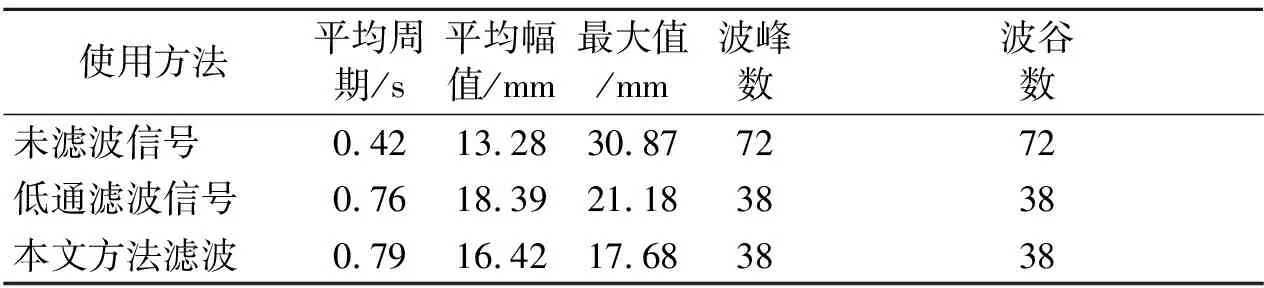
表1 3种方法的统计结果比较
4 结论
1)耐波性试验测量数据受噪声的影响,直接进行数据分析影响分析精度。
2)基于低通滤波及EMD的联合分析方法能够过滤高频噪声及低频趋势项的影响,提高数据分析的精度及效率。
3)开发的数据处理系统界面友好,操作简易,且能够执行多通道数据的批处理,并对海量数据进行有效的统计分析,能够实现耐波性试验数据的实时处理;可为船舶耐波性能的优化设计和综合评价提供有力的技术支撑。
[1] 陈 隽,李 杰.振动信号趋势项提取的几种方法及其比较[J].福州大学学报,2005,33(S):42-45
[2] 许 勇,欧勇鹏,董文才.基于低通滤波和经验模态分解的舰船耐波性试验信号分析方法研究[J].船舶力学,2009,13(5):712-717.
[3] 许 勇,董文才,欧勇鹏.基于FFT-FS频谱细化技术的船模乃波形试验测量信号分析方法研究[J].船舶力学,2012,16(5):497-503.
[4] 彭英声.舰船耐波性基础[M].北京:国防工业出版社,1988.
[5] CHIN T W,MIAU J J.Mode decomposition analysis applied to study the low-frequency embedded in the vortex shedding princess[C]∥The 27th Conference on Theoretical and Applied Mechanics,TaiWan,2003:93-124.
[6] 赵 霞,熊小伏,郭 珂.用细化频谱技术分析断路器操动机构振动信号[J],电力系统自动化,2003,27(12):37-41.
[7] 刘 维.实战MATLAB之并行程序设计[M].北京:北京航空航天大学出版社,2012.
[8] 许 勇.波浪中近距离航行的多船水动力干扰机理研究[D].武汉:海军工程大学,2012.
