配筋活性粉末混凝土梁抗剪承载力

邓宗才，周冬至，程舒锴

（北京工业大学城市与工程安全减灾省部共建教育部重点实验室，北京100124）

配筋活性粉末混凝土梁抗剪承载力

邓宗才，周冬至，程舒锴

（北京工业大学城市与工程安全减灾省部共建教育部重点实验室，北京100124）

为掌握高强箍筋活性粉末混凝土（reactive powder concrete，RPC）梁的抗剪性能，通过6根T形梁的抗剪试验，获得了抗剪承载力试验值，并将试验值与压力场理论值进行了比较，探讨了压力场理论应用于RPC梁抗剪分析和承载力计算存在的问题，充分考虑斜裂缝截面上钢纤维拉拔阻力的抗剪贡献，对该理论进行了改进。并将剪切试验结果与塑性剪切理论、粘结滑移理论和法国规范等进行了比较，分析现有抗剪理论的适用条件、存在的问题，这些对揭示RPC梁抗剪破坏机理、建立承载力计算理论与设计方法有参考价值。

修正压力场理论；塑性剪切理论；界面粘结理论；抗剪强度；活性粉末混凝土

活性粉末混凝土（reactive powder concrete，RPC）是由法国Bouygues试验室于1993年研制出的一种具有超高强度、高耐久性、高韧性的新型水泥基复合材料，它由石英砂、水泥、硅灰、高效减水剂及钢纤维等组成。RPC在核工程结构、超高超大结构、防爆及防冲击结构、抗腐蚀结构以及桥梁等重要工程中显示出独特的优越性和广阔的应用前景。

自RPC问世以来，国内外学者对其强度、韧性、抗渗性、疲劳断裂、抗冲击性［1-5］等材料性能进行了较多的研究，但关于抗剪性能的研究较少。美国学者Jun Xia和Kevin R.M［6］，澳大利亚新威尔士大学Voo、Foster、Poon［7-8］等进行了一系列无腹筋RPC梁的抗剪试验。我国学者季文玉［9］等进行了RPC配腹筋T形梁的抗剪试验，研究了梁剪切破坏形态和承载力的主要影响因素。国内外的试验发现：由于RPC中掺有钢纤维，不仅提高了承载力，而且也使得梁的剪切破坏机理与普通混凝土梁不同。如何科学地解释RPC梁的剪切破坏全过程和揭示其破坏机理，建立合理的承载力预测模型，是目前面临的主要问题之一。20世纪80年代加拿大多伦多大学试验室提出的修正压力场理论［10］（以下简称压力场理论）开辟了一条研究受剪破坏机理的新途径，该理论已被加拿大、美国桥梁设计规范等采用。压力场理论与经典桁架模型的主要区别是：压力场理论针对危险截面附近的微单元进行分析，而古典桁架理论则将梁比拟为桁架。压力场理论可以分析由开裂到梁破坏的全过程，考虑了开裂后混凝土的抗剪贡献和裂缝截面骨料咬合作用等。但压力场理论是针对普通混凝土提出的，未考虑RPC中钢纤维的抗剪贡献，因此有必要考虑钢纤维拉拔阻力对压力场理论进行修正和完善。另外，最近几年Voo［11］等结合钢纤维RPC梁的抗剪性能试验结果，提出了塑性剪切理论和粘结滑移理论等，法国规范也给出了钢纤维RPC抗剪承载力的计算公式。需要结合试验结果对这些理论模型进行综合比较，发展适合于钢纤维RPC梁的抗剪强度理论和承载力计算方法，为工程应用提供依据。

1 试验与压力场理论

1.1 试验概况

试验设计了6根活性粉末混凝土T型梁，其中3根无腹筋，分别记为L1、L2、L3；3根有腹筋梁，分别记为L4、L5、L6。梁的截面尺寸相同，如图1所示。试验梁先养护静置自然养护3 d，然后蒸汽养护2 d（温度≥90℃，相对湿度90%以上），最后自然养护23 d至开始试验。制备RPC所用原材料：P.O 52.5超细水泥，比表面积600 m2／kg；P.O 42.5普通水泥，比表面积360 m2／kg；S95级粒化高炉矿渣，比表面积408 m2／kg；粒径小于1 mm的石英砂；西卡高效聚羧酸减水剂。直径0.12 mm、长8mm的I型平直镀铜钢纤维；直径0.21 mm、长13mm的II型平直镀铜钢纤维。RPC配合比：超细水泥236 kg／m3，普通水泥471 kg／m3，矿渣471 kg／m3，石英砂1 070 kg／m3，外加剂1.2%，水胶比0.17，钢纤维118 kg／m3，其立方体抗压强度平均值为132 MPa。梁纵筋采用HRB500高强钢筋，配筋率均为4.69%；有腹筋梁的箍筋采用HRB500钢筋，配箍率均为0.24%。

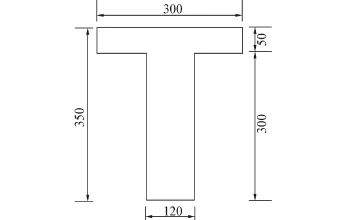
图1 梁的截面尺寸（单位：mm）Fig.1 The section size of beam（unit：mm）

1.2 试验结果与压力场理论值的对比

为验证用压力场理论计算RPC梁抗剪承载力的适用性，将压力场理论值与本文3根有腹筋梁的抗剪试验结果及季文玉等的抗剪试验值［9］进行了对比。季文玉的剪切梁为RPC T形梁，剪跨比由2～4；纵筋HRB335，配筋率9.47%～13.573%；箍筋HPB235，配箍率0～0.837%.同时将试验结果与我国《高强混凝土结构技术规程》［12］进行了比较.理论值与试验值的比较列于表1。

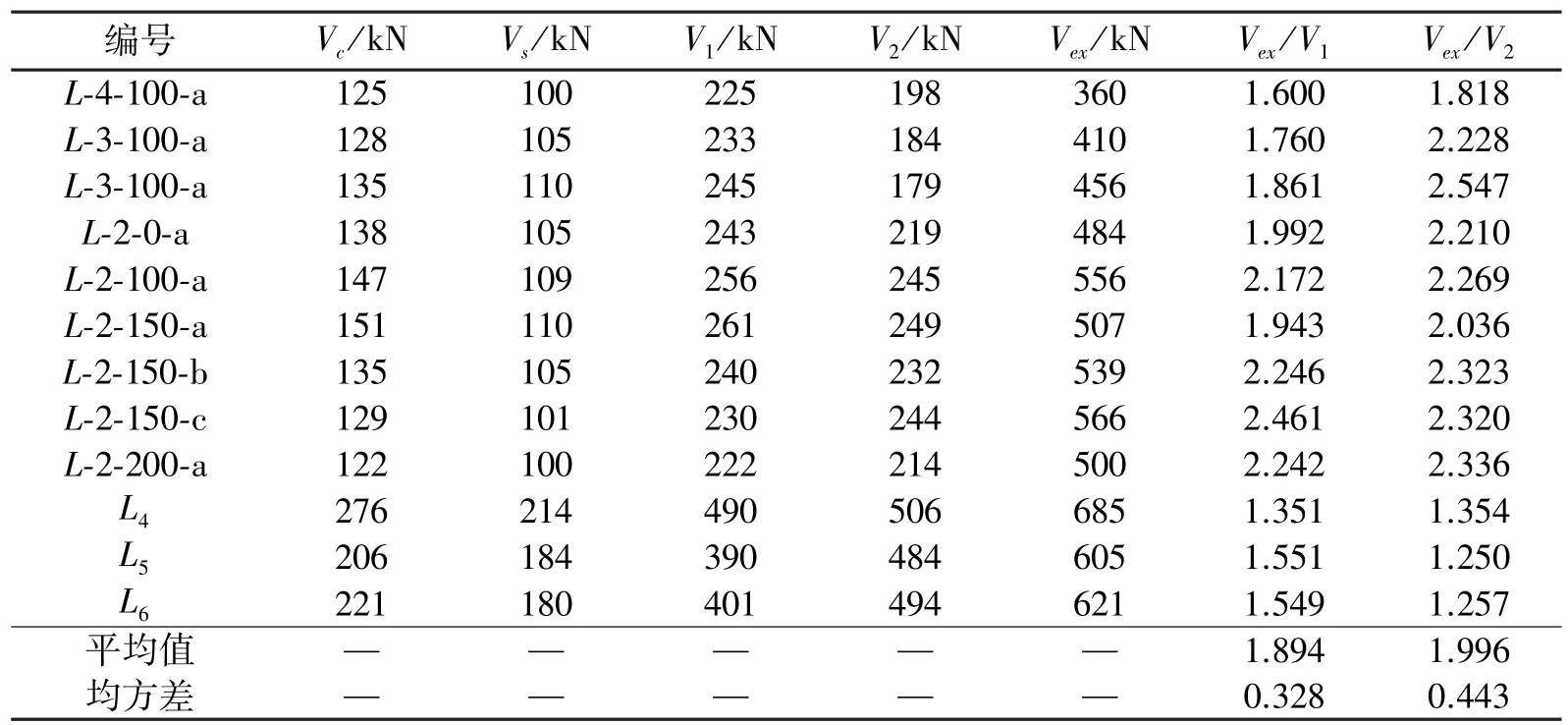
表1 试验结果与压力场理论和《高强混凝土结构技术规程》比较Table 1 Comparison of the test results with values by compression field theory and“Technical Specification for High-Strength Concrete Structures”

表1中Vc表示压力场理论中RPC承担的剪力；Vs表示箍筋承担的剪力；V1为按压力场理论计算出的抗剪承载力，V1＝Vs＋Vc；V2表示《高强混凝土结构技术规程》理论值；Vex为抗剪承载力试验值。

由表1看出，试验值明显大于压力场理论和《高强混凝土结构技术规程》的计算值，试验值与理论值比值的平均值分别为1.894和1.996。如果将压力场理论直接用于计算配箍RPC梁抗剪承载力时误差较大。

1.3 压力场理论的完善

由表1试验值与压力场理论值的对比可知，压力场理论不能直接用于计算RPC梁的抗剪承载力，该理论低估了RPC梁的抗剪承载力。分析其原因有：1）压力场理论是基于普通钢筋混凝土构件抗剪试验得来的，而RPC中含有钢纤维，当梁出现斜裂缝后，裂缝截面上钢纤维的拉拔阻力，对抗剪有一定贡献，这部分抗剪作用不能忽略；2）压力场理论认为：当发生剪切破坏时，梁腹部会出现大量斜裂缝，腹部混凝土承担了主要剪力，而忽略了受压区混凝土提供的抗剪作用。因此需要根据RPC材料自身的应力-应变模型，考虑斜裂缝截面钢纤维的拉拔阻力，利用裂缝间力的平衡条件、变形协调方程、跨越裂缝区力的平衡等，提出适合配筋RPC梁的压力场理论。

1.3.1 裂缝间力的平衡

截面剪力由斜拉应力f1和斜压应力f2承担，f1、f2为平均应力值。与普通混凝土不同的是由于钢纤维的存在，在裂缝处RPC的拉应力不为零，RPC开裂后仍可继续承担拉应力。由摩尔圆得到

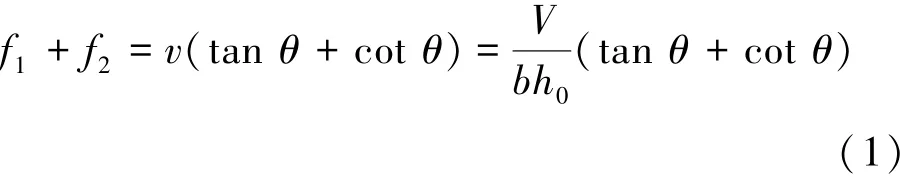
式中：b为截面宽度，h0为内力臂，V为抗剪承载力，θ为斜裂缝与纵筋的夹角。

竖向不平衡力由箍筋承担，即

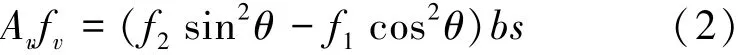
由式（1）、（2）得：

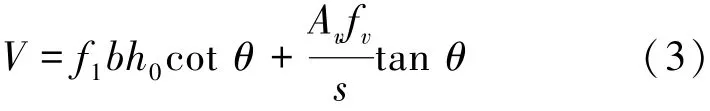
式中：第1项为钢纤维增强RPC对受剪承载力的贡献，第2项为箍筋承担的剪力。

1.3.2 跨越裂缝的力的平衡

在剪力作用下，实际出现的斜裂缝比较复杂，分析时假定斜裂缝为互相平行的平面，与纵向钢筋的夹角为θ。当剪力较小时，拉力通过箍筋应力的局部增加而穿越裂缝传递。当剪力达到一定值时，裂缝处的箍筋达到屈服强度。当剪应力较高时，跨越裂缝传递的拉应力要求在裂缝表面产生局部剪应力vci。裂缝处和裂缝间的2组应力必须相等，如图2所示，竖向力相等得

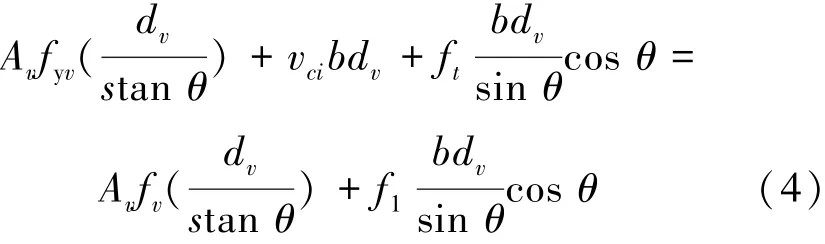
由式（4）得平均拉应力f1为

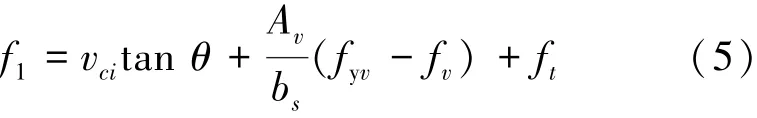
式中：fyv为裂缝处箍筋屈服强度，fv为裂缝间箍筋的拉应力值，ft为钢纤维提供的拉拔应力。

由式（5）可见，依赖于f1的纤维增强RPC的抗剪贡献是通过裂缝处骨料咬合作用、纤维的拉拔阻力和跨越裂缝的箍筋应力增量而实现的。

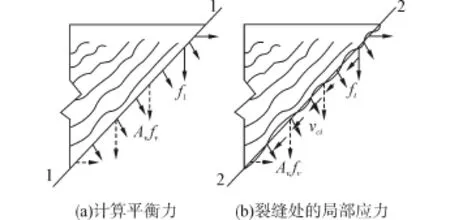
图2 跨越裂缝传递力Fig.2 Cross crack propagation force

1.3.3 应变协调

据单元平均应变和应变摩尔圆，采用应变摩尔圆表示的几何变换建立开裂截面的应变协调关系，得到压杆的倾角为

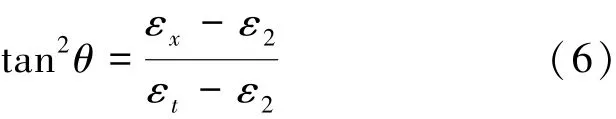
由材料第一应变不变量得到下面关系：

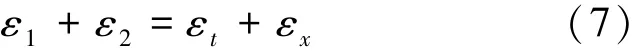
1.3.4 开裂RPC及钢筋应力－应变关系

开裂后RPC拉应力－应变关系［13-14］：

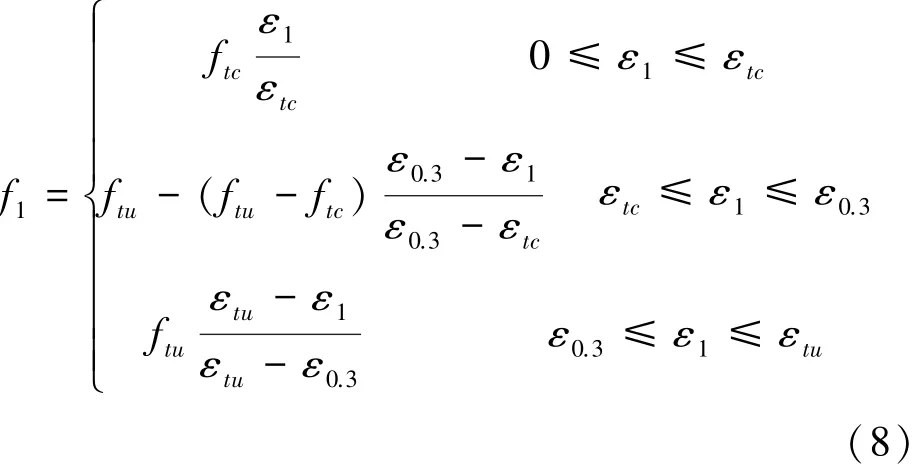
式中：ftc为单轴拉伸初裂应力；ftu为轴拉强度；εtc为RPC初裂应变；ε0.3为裂缝宽度0.3 mm时对应的拉应变，取为梁高；εtu＝为钢纤维长度。

钢筋应力-应变关系采用理想弹塑性模型。

将上述的力平衡条件、变形协调方程和材料的应力-应变关系联立起来，构成了按压力场理论求解纤维增强RPC梁抗剪承载力的方程组。解这些方程组可求解出未知的应力、应变和角度θ，进而当裂缝处箍筋达到屈服时，求得梁的抗剪承载力。

然而上述求解过程较为繁琐，拟采用已有的优化方法解决［15］，为此构造目标函数：

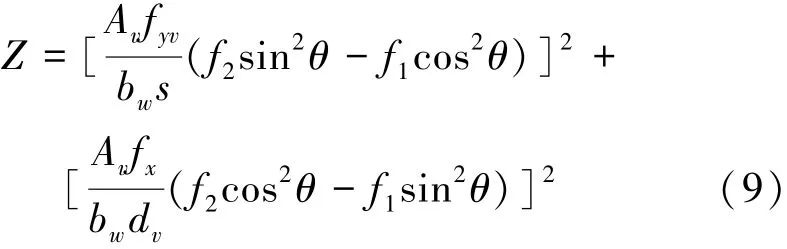
以变量θ和ε1作为优化变量使得构造的目标函数Z＝0（实际计算中足够小即可）时，可求出梁抗剪承载力V。表2同时列出了采用完善后的压力场理论计算的抗剪承载力和试验值。表中Vc′表示完善后的修正压力场理论中RPC承担的剪力；Vs′为箍筋承担剪力；V1′表示完善后的压力场理论计算出的抗剪承载力，V1′＝Vs＋Vc；Vex为试验值。

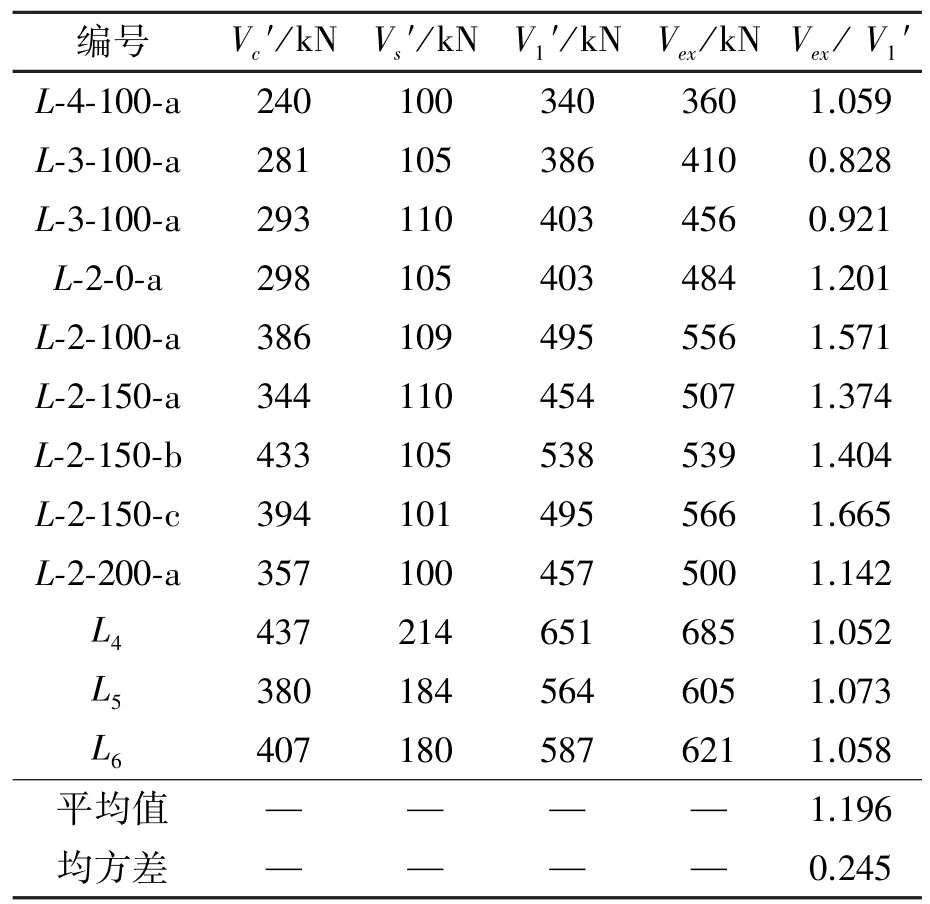
表2 试验结果与完善后的修正压力场理论值的比较Table 2 Comparison of test results with the modified compression field theory

可以由表2看出：1）按完善后的修正压力场计算出的抗剪承载力与试验值比较接近，试验与理论值的比值的平均值为1.196，相对于修正之前的1.894有了很大的改善；2）按照完善后的压力场理论计算的RPC抗剪贡献比按原压力场理论值提高58.4%，修正的压力场理论考虑了裂缝截面钢纤维的抗剪贡献，该理论模型更能反映材料的特性。因此完善后的压力场理论对于RPC梁比较适用，可用于分析配箍RPC梁的剪切破坏机制和进行承载力计算。

2 其他抗剪理论

2.1 塑性剪切理论

由于RPC中掺入钢纤维，显著提高了RPC梁的变形能力和抗剪能力。当RPC梁开裂后，由于众多钢纤维的阻裂，使得斜面裂缝扩展缓慢，梁的变形具有明显的塑性变形特征。据此，澳大利亚新威尔士大学的Voo等人［7-8］基于上限塑性理论，在裂缝滑移模型的基础上，考虑了钢纤维对RPC的增韧，提出了无腹筋RPC梁抗剪承载力计算公式：

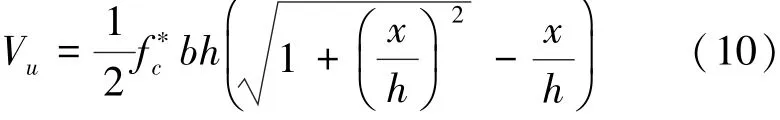
式中：f*c是RPC抗压强度，b为梁宽度，h为梁高度。x为裂缝的水平投影长度，计算时采用试验实测值。将Voo等人的试验值、塑性剪切理论计算值列于表3。表中Vpu表示按塑性理论计算出的抗剪承载力；Vex为试验值。

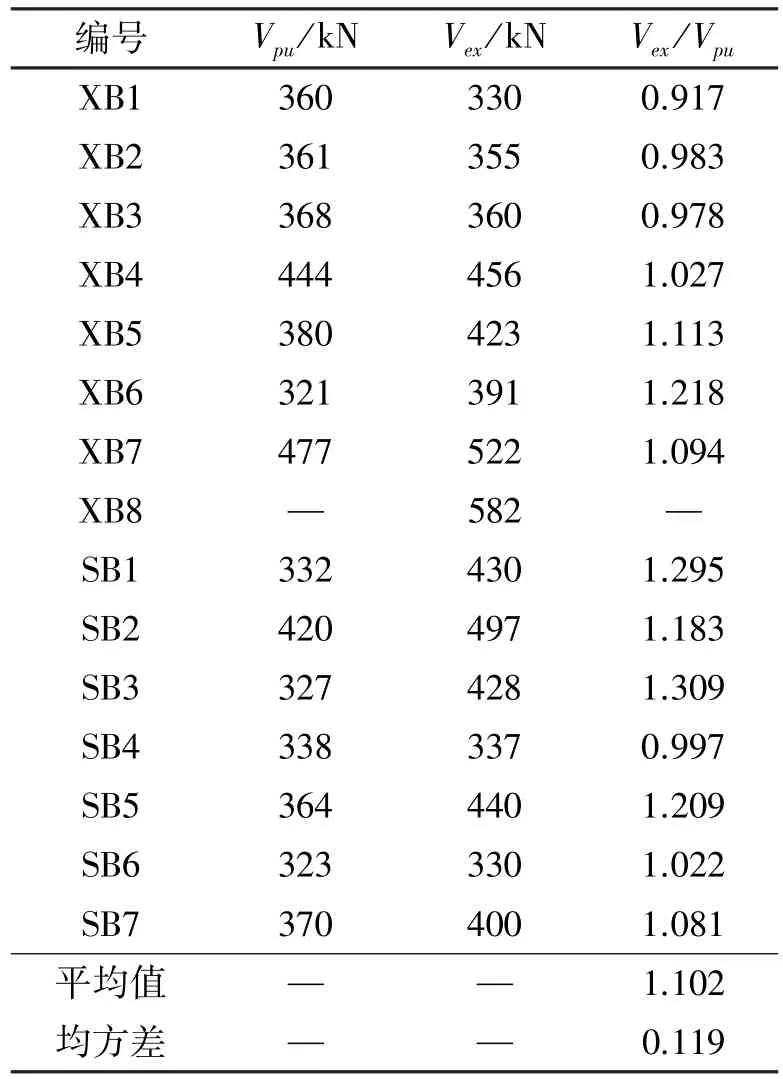
表3 试验结果与塑性剪切理论值的比较Table 3 Comparison of test results with the plasticity shear strength theory

由表3看出，试验值与塑性理论计算值较为接近。虽然塑性剪切理论值与试验值比较接近，平均值为1.102，均方差为0.119，但是在求承载力时必须先知道斜裂缝水平投影长度x。求解x的方法如下：Voo等人完善了塑性剪切理论［7-8］，先求出RPC开裂时剪力，即

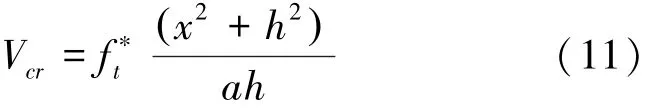
式中：f*t为钢纤维RPC抗拉强度。为求解裂缝夹角θ，Voo等人假定RPC梁的开裂剪力Vcr和极限承载力Vu相等，联立式（10）和式（11）得：

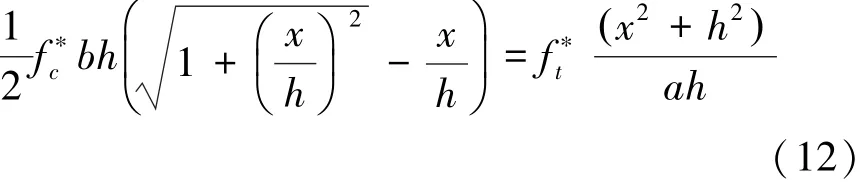
解等式（12），求出x值，进而求出裂缝夹角θ，将θ理论值和试验值列于表4。

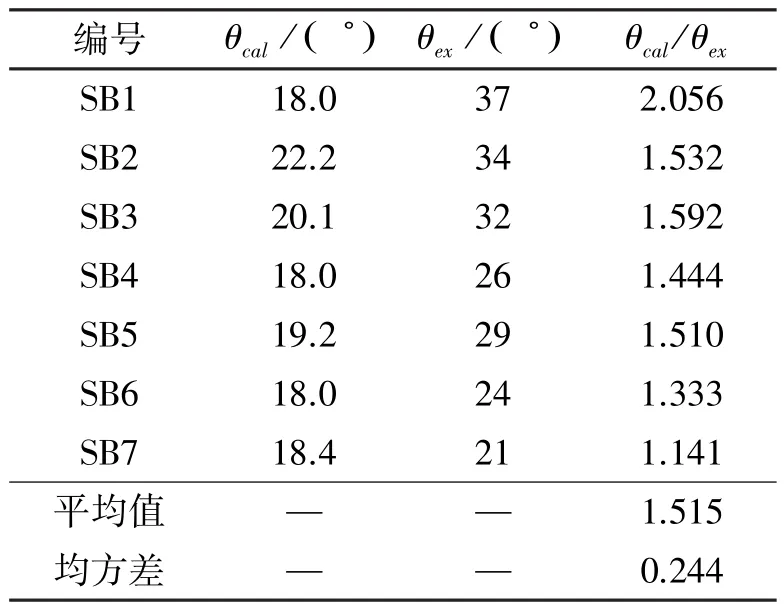
表4 θ理论值与试验值的比值Table 4 Comparison of the calculated included angle θ with test results

由表4可以看出，θ试验值与理论值比值的平均值为1.515，即裂缝长度实测值明显大于裂缝长度理论值。分析原因是：在塑性剪切理论中，假定裂缝与水平轴的角度θ固定不变，而由试验可知角度θ是随外力的变化而是不断变化的。

2.2 界面粘结滑移理论

斯图加特大学Reineck［11］等人基于“齿模型”（如图3示），认为梁的抗剪承载力依赖于混凝土与钢筋界面粘结强度，假定梁开裂后被分成只在顶部受压区连接的齿状模型。

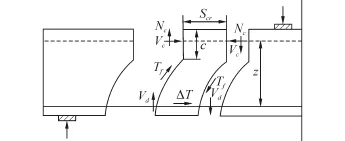
图3 齿模型受力分析图Fig.3 Tooth model and load transfer analysis

据图3所示单个齿状块的受力状况，利用力矩平衡得到

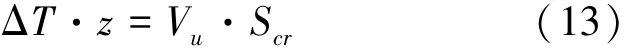
式中：Vu表示梁受剪承载力，包括来自于素RPC、钢纤维和纵筋销栓作用提供的剪力；Scr表示2条裂缝间的距离；z表示梁受拉区形心到受压区形心的力臂长度；ΔT表示单个齿状块内部总粘结拉力，ΔT表达式为

式中：τu表示纵筋与PRC界面粘结强度；ds表示参与受拉滑移的纵筋直径；πdsScr为总粘结面积。由式（13）、（14）得到RPC梁受剪承载力为

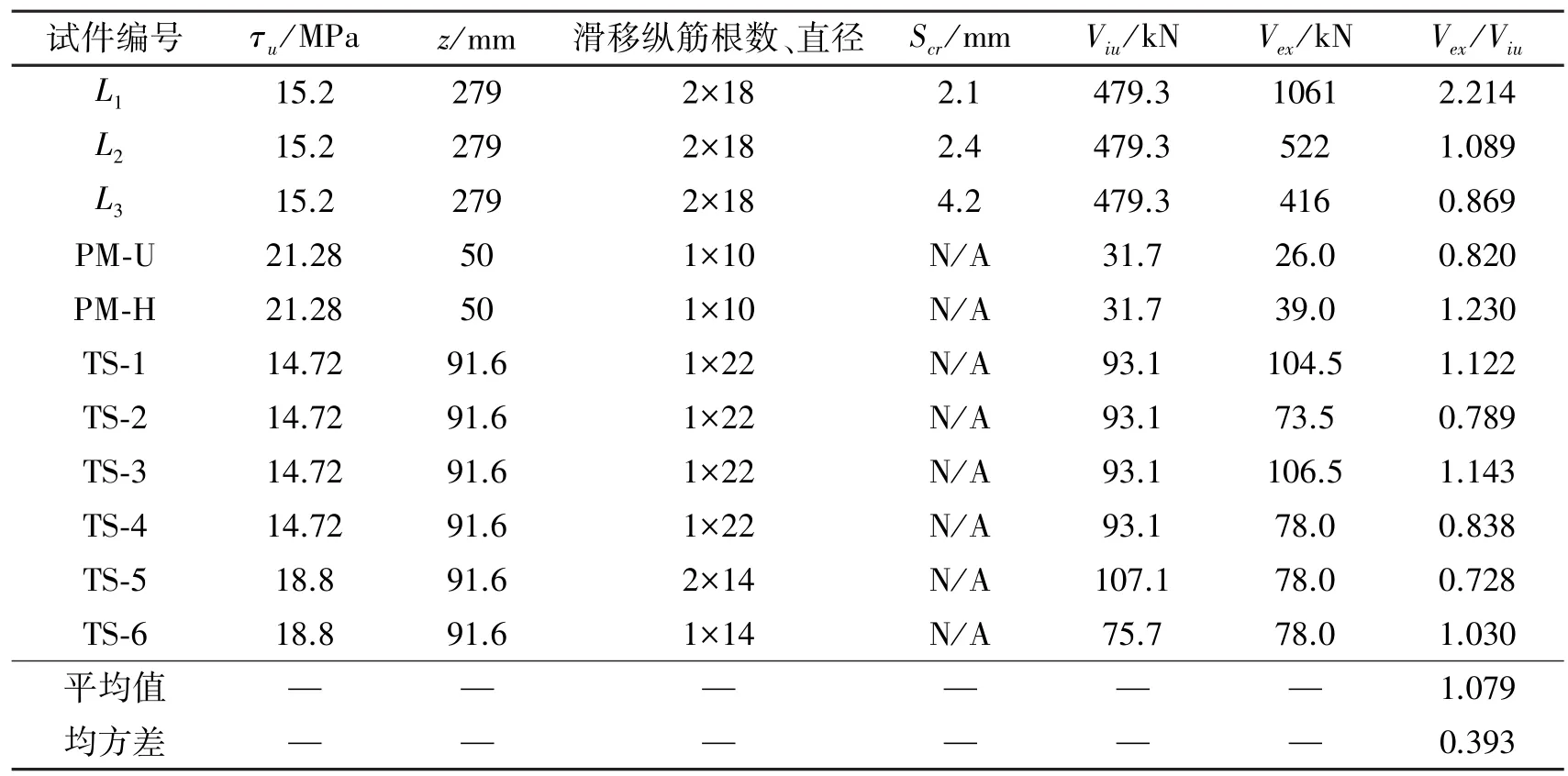
表5 试验结果与界面粘结滑移理论值比较Table 5 Comparison of test results with value by the interfacial bond shear strength theory

由表5可见，界面粘结滑移理论值与试验值较为接近，试验值与理论值比值的平均值为1.079，均方差为0.393。分析试验与理论值不同的原因有：1）梁L1试验值远大于理论值，其主要原因是界面滑移模型未能反映剪跨比对承载力的影响。梁L1剪跨比为1，发生了剪压破坏。即界面滑移理论不适合剪压破坏试件。2）界面粘结理论计算时需合理选取参与受拉滑移纵筋的数目，若纵筋根数较少，则全部纵筋参与计算；如果纵筋分布密集，纵筋将会出现并根滑移现象。对于并根滑移需通过并根钢筋的拉拔试验确定其粘结强度。3）钢筋与基体界面粘结强度由钢筋拉拔试验的极限荷载求得，而梁受力过程中纵筋一般只是产生相对滑移，未达到完全粘结破坏，若按照极限拉拔荷载计算，高估了抗剪承载力。4）由式（15）可知抗剪承载力理论值与裂缝间距Scr无关，但裂缝间距会影响到界面粘结应力，而界面粘结力影响承载力。

2.3 法国规范

法国规范［14］中，把配腹筋RPC梁的抗剪承载力分为素RPC、箍筋和钢纤维3部分。

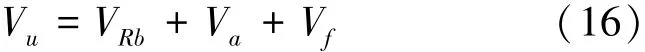
式中：VRb、Va、Vf分别表示素RPC、腹筋和钢纤维承担的剪力。

法国规范中素RPC承担的剪力的计算式为

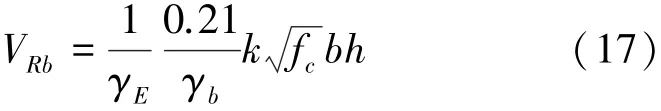
式中；fc表示素RPC的圆柱体轴心抗压强度；k表示预应力影响系数；γE·γb为考虑到试件RPC强度的不确定性而引入的安全系数，取1.5；h、b分别表示梁的高度和宽度。

箍筋承担的剪力Va按照45°桁架模型公式计算，即

式中：Av表示同一截面内箍筋各肢的全部截面面积，s为箍筋间距，h0为梁截面有效高度，fv为箍筋抗拉强度设计值。

钢纤维承担的剪力Vf表示为

式中：S＝bz表示纤维作用区域的面积，其中z为拉压区抵抗力矩的力臂长度，矩形截面梁可取值为梁高h的0.9倍；θ表示斜裂缝与水平轴夹角；γbf为考虑到人为影响因素的安全系数，在法国规范中荷载为基本组合时取1.3，偶然组合时取1.05。

梁开裂后裂缝处钢纤维增强RPC拉应力为

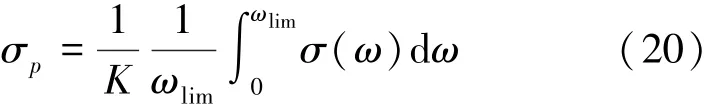
式中：K为考虑到钢纤维方向的影响因子，一般情况取1；ωlim表示裂缝宽度的限值；σ（ω）表示RPC裂缝宽度与拉应力之间的关系，由RPC单轴拉伸试验测得。

将式（17）～（20）代入式（16）中可计算出梁的抗剪承载力Vfu。将本文6根梁的试验结果和Jun Xia等人的试验值［6］、法国规范抗剪承载力理论值［14］列于表6。表中Vf为钢纤维承担的剪力值，Vfu为法国规范求得的梁抗剪承载力，Vex为梁抗剪承载力试验值。

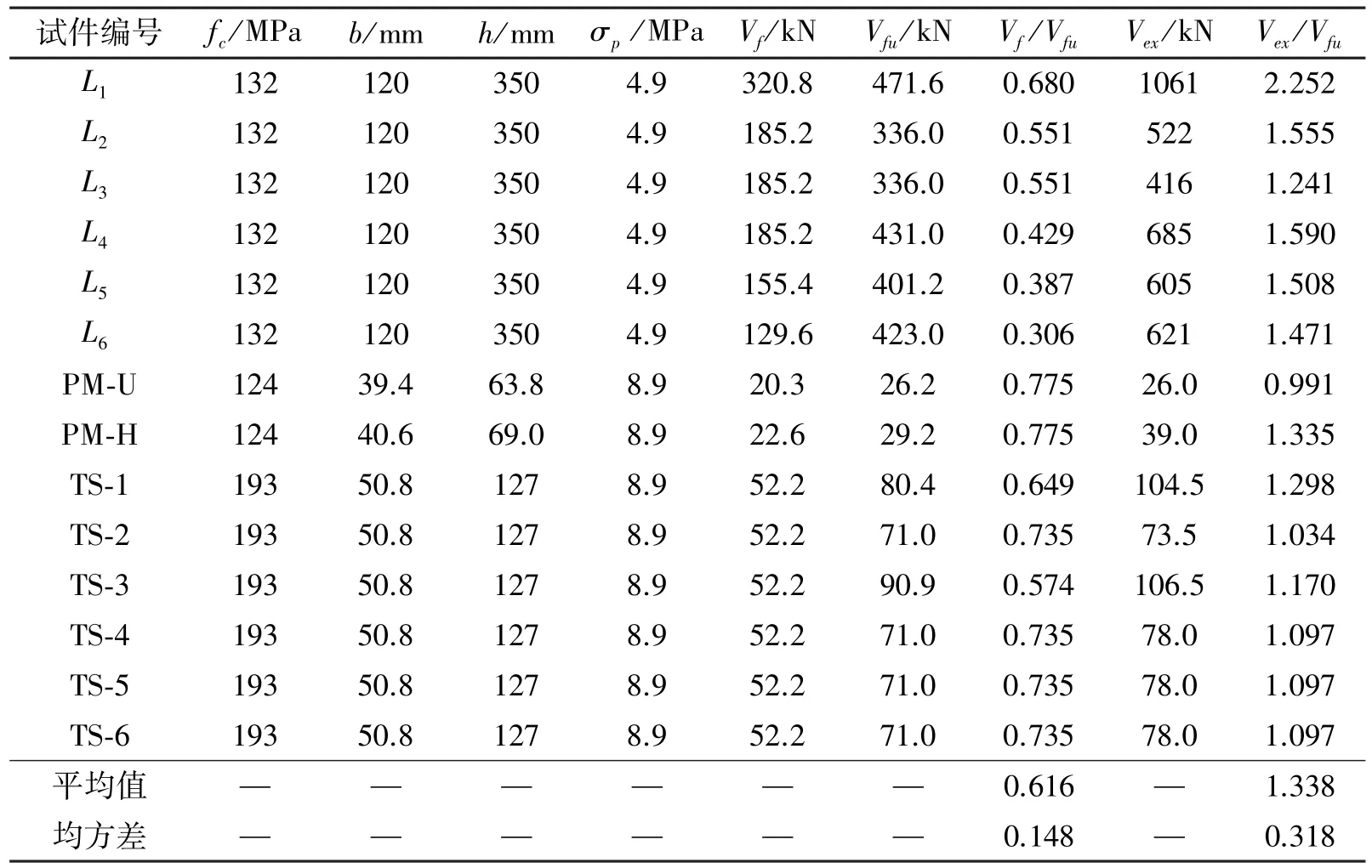
表6 试验结果与法国规范公式计算值的比较Table 6 Comparison of test results with the value calculated by French Code

由表6可知，试验结果明显大于法国规范值，最大的达到了2.252倍，平均值为1.338倍。试验值明显大于理论值的原因为：1）规范中素RPC抗剪承载力是按照素高强混凝土给出的，低估了高强RPC的抗剪贡献，该值需要进一步研究。2）法国规范是针对矩形梁提出的，对T形梁计算中该公式未考虑翼缘部分的抗剪，计算值偏于安全。3）剪跨比影响梁斜裂缝角度，从而影响钢纤维作用面积，有必要研究纤维掺量、剪跨比对斜裂缝角度的影响。

按法国规范求得钢纤维抗剪贡献Vf约占总抗剪承载力计算值的30.6%～77.5%，可见钢纤维对梁抗剪贡献较大。

3 结论

1）在抗剪试验基础上，据钢纤维RPC材料特性，考虑了斜截面上钢纤维拉拔阻力对抗剪的贡献，对压力场理论进行了完善，完善后的压力场理论可用于解释RPC梁抗剪破坏机制，具有明确的物理含义，理论值与试验值比较接近，可用于计算抗剪承载力。

2）通过与梁抗剪试验值比较，分析了塑性剪切理论、界面粘结理论及法国规范用于RPC抗剪承载力计算存在的问题。试验值与塑性剪切理论值较为接近，比值为1.102，但该理论假定斜裂缝角度沿梁高不变，实际上斜裂缝按曲线路径扩展，角度不断变化。试验与界面粘结滑移理论值的比值为1.104，该理论未能反映剪跨比、裂缝间距对承载力影响；当纵筋根数较少时，该理论计算较为准确。

3）法国规范、基于塑性上限理论的塑性剪切模型均考虑了纤维的抗剪贡献，钢纤维提高了RPC梁的抗剪承载力，裂缝处钢纤维拉拔阻力提供的抗剪贡献不能忽略，约占RPC梁承载力的30.6%～77.5%。

［1］SHAHEEN E，SHRRIVE N G.Optimization of mechanical properties and durability of reactive powder concrete［J］.ACI Mater J，2006，103（6）：444-451.

［2］BAYARD O，PLE O.Fracture mechanics of reactive powder concrete：material modeling and experimental investigations［J］.Eng Fract Mech，2003，70（7／8）：839-851.

［3］DUGAT J，ROUX N，BERNIER G.Mechanical properties of reactive powder concretes［J］.Mater and Struct，1996，29（188）：233-240.

［4］RICHARD P，CHEYREZY M.Composition of reactive powder concretes［J］.Cem Concrete Res，1995，25（7）：1501-1511.

［5］RICHARD P，CHEYREZY M.Reactive powder concrete with high ductility and 200-800MPa compressive strength［S］.San Francisco：ACI SP，1994：507-518.

［6］XIA Jun，KEVIN R M.Shear failure analysis on ultra-high performance concrete beams reinforced with high strength steel［J］.Engineering Structures，2011，33：3597-3609.

［7］VOO Y L，POON W K，FOSTER S J.Shear strength of steel fiber-reinforced ultrahigh-performance concrete beams without stirrups［J］.Structural Engineering，2010，136（11）：1393-1400.

［8］VOO Y L，FOSTER S J，GILLBERT R I.Shear strength of fiber reinforced reactive powder concrete prestressed girders without stirrups［J］.Advanced Concrete Technology，2006，4（1）：123-132.

［9］季文玉，丁波，安明喆.活性粉末混凝土T形梁抗剪试验研［J］.中国铁道科学，2011，32（5）：38-41.JI Wenyu，DING Bo，AN Mingzhe.Experimental study on the shear capacity of reactive powder concrete T-beams［J］.China Railway Science，2011，32（5）：38-41.

［10］MITCHELL D，COLLINS M P.Diagonal compression field theory—a rational model for structural concrete in pure torsion［J］.ACI Journal，1974，71（8）：396-408.

［11］REINECK K H.Ultimate shear force of structural concrete member without transverse reinforcement derived from a mechanical model［J］.ACI Struct J，1991，88（5）：592-602.

［12］CECS 104：99.高强混凝土结构技术规程［S］.北京：中国建筑工业出版社，1999.

［13］TAYLOR W C，MONTOYA K F，JAUREGUI D V，et al.Feasibility analysis of using UHPC in prestressed bridge girders［C］／／Proceedings of the 2011 Structures Congress.Las Vegas，USA，2011：203-214.

［14］AFGC.Ultra high performance fibre-reinforced concretes［M］.Paris：AFGC Publication，2002：257-268.

［15］贡金鑫，魏巍巍.现代混凝土结构基本理论及应用［M］.北京：中国建筑工业出版社，2009：186-199.

The shear bear capacity of reactive powder concrete beam with high strength stirrup

DENG Zongcai，ZHOU Dongzhi，CHENG Shukai
（The Key Laboratory of Urban Security and Disaster Engineering，Ministry of Education，Beijing University of Technology，Beijing 100124，China）

To grasp the shear strength properties of reactive powder concrete（RPC）beams with high strength stirrup，through 6 T-shaped beams test，the shear strength test values were obtained.The test values and the theoretical values of the compression field theory were compared and the questions of applying the compression field theory in the analysis and calculation of shear capacity for RPC beams were also discussed.The modified compression field theory was proposed by considering the shear crack resistance improvement from the contribution of the steel fibers at the diagonal crack during pull out.Results of the shear test were also compared with the plastic shear theory，the interfacial bond shear strength theory and French code specifications.An analysis of problems facing the existing theories and their applications was also conducted.The analysis results and comparison conducted on the different shear capacity theories provided a solid base for future researches on the shear failure mechanism and further development of shear capacity design models for RPC beams.

modified compression field theory；plasticity shear strength theory；interfacial bond theory；shear strength；reactive powder concrete

10.3969／j.issn.1006-7043.201308015

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006－7043.201308015.html

TU375.3

A

1006-7043（2014）12-1512-07

2013-08-15.网络出版时间：2014-12-02.

国家自然科学基金资助项目（51378032）；北京市自然科学基金资助项目（8142005）；教育部博士点基金资助项目（20131103110017）.

邓宗才（1961-），男，教授，博士生导师.

邓宗才，E-mail：dengzc＠bjut.edu.cn.