阻抗梯度变化介质的声学特性

杨德森，孙玉，胡博，韩闯，靳仕源

（哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨150001）

阻抗梯度变化介质的声学特性

杨德森，孙玉，胡博，韩闯，靳仕源

（哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨150001）

阻抗梯度变化介质是从多层复合介质领域脱颖而出的一种声学介质，它是通过选取具有不同特征阻抗的材料，从阻抗匹配的角度组成特性阻抗成梯度变化的介质，从而获得更好的声学性能。针对水中声学介质的声传播问题，建立了阻抗梯度变化介质中的声传播模型，对其声学特性进行了研究，推导了阻抗梯度变化介质的反射、吸声系数的计算公式。通过仿真计算，将阻抗梯度变化介质与传统均匀介质的声学性能相对比，讨论离散计算中介质层数的选取原则。制备了阻抗梯度变化介质，进行了水下声学性能测量实验，实验结果表明：实验介质的阻抗具有良好的连续性分布能够满足实验要求，测量结果验证了阻抗梯度变化介质更小的反射系数和更大的吸声系数，为阻抗梯度变化介质在水声工程中的应用提供了理论依据。

声阻抗；梯度变化；声学特性；反射系数；阻抗匹配；声学介质

众所周知，提高分层介质声学性能最直接的方法就是使介质表面的输入阻抗与自由空间波阻抗相匹配，同时要求介质具有很高的声衰减性能［1-2］，但这2个条件本身就是矛盾的，对于均匀介质无法同时满足。深入研究发现，当介质的阻抗或结构呈梯度变化时能够满足以上2个条件。据此，通过改变介质的结构、物理和化学特性的方法，人们设计了多种声学介质，并对介质的声学性能进行了研究。

Beretti［3］研究了具有4层结构的消声层的声学特性，发现在不增加消声材料厚度的情况下，由多种材料组成的多层结构具有消声和减振功能。Emer-y［4］对阻抗渐变的多层结构进行了研究，指出在高频时阻抗匹配可以减小反射系数，低频时通过采用不同厚度、阻抗的多层结构可以解决反射系数的峰值问题。Andrew［5］针对不同高度会引起空气中声速和阻抗的变化这一现象，对多个高度下大气层的声传播问题进行了研究。何祚镛［6-7］对声垂直入射时水下均匀和非均匀材料复合层的声学特性进行了研究，提出了计算包含任意非均匀层的多层复合结构反射、吸声系数的近似方法。朱金华［8］选取3种不同材料组合成梯度聚氨酯材料，研究了梯度聚氨酯介质中的声吸收，但结果发现这种制作方法并非十分理想，不同阻抗的材料分界面会影响声波的发射和透射。杨雪［9-10］采用浇注的方法制备了梯度聚氨酯，研究在全入射角下梯度聚氨酯的吸声性能，但这种逐层浇注的方法仍然存在每层材料的阻抗不连续的问题。王源升［11-12］设计合成了多种不同配方的梯度高分子溶液，通过声波在梯度层中被多次反射吸收实现声波有效衰减，但这种溶液在实用性和可控性方面还存在很大问题。目前，人们的研究只限于对不同材料组成的梯度声学介质的可行性研究，而对于阻抗梯度变化介质中声传播机理问题，人们没有作更深入的研究，已有的方法也只是将介质分层，再将每层介质中的阻抗看成均匀的进行求解，而这种计算方法会存在很大误差。在制备方面，理想的阻抗梯度变化介质的阻抗应连续梯度变化，内部不存在明显的界面，从而使介质的性质和功能沿厚度方向也成梯度变化，但目前制备的梯度介质仍存在阻抗不连续和实用性差等问题。

本文以水中消声材料为研究背景，设计了阻抗连续梯度分布的不均匀介质，达到介质表面阻抗匹配和内部高损耗的目的。建立了阻抗梯度变化介质中的声传播模型，对介质中声传播规律进行了研究，推导了任意阻抗分布条件下介质的吸声系数、反射系数公式。进行仿真研究，将阻抗梯度变化介质结构与传统均匀介质的声学性能比较。最后设计制作了阻抗连续梯度变化介质，采用脉冲声管法对其水下声学性能进行了测量。

1 阻抗梯度变化介质中声传播理论

1.1 声传播规律

假设有2个半空间无限均匀介质，分别为介质I和介质III，阻抗分别为Z1和Z3，密度分别为ρ1和ρ3，声速分别为c1和c3。在它们之间有介质II，介质II的特性阻抗Z（x）设计为在迎声面处与Z1匹配，在介质另一侧与Z3匹配，介质II的厚度为d。为满足介质阻抗匹配和高衰减的要求，可以将介质II的阻抗值设计成在厚度方向上按一定规律呈连续变化。图1为介质II的阻抗分布图。设计时主要考虑以下几点：1）介质表面阻抗匹配。只有先将声波“引”进来，才有可能在介质内部对其进行吸收和衰减，因此应保证介质表面的输入阻抗与自由空间的阻抗匹配；2）保证阻抗连续变化。应保证介质内部阻抗变化的连续性，减小介质内部声波的反射；3）实现高衰减高吸收。当声波被引入介质内部后，必须具有足够大的声能量损耗才能对声波进行衰减吸收，因此将介质的阻抗设计成逐渐增大变化。最终使阻抗梯度变化介质获得更小的反射系数更小和更大的吸声系数。

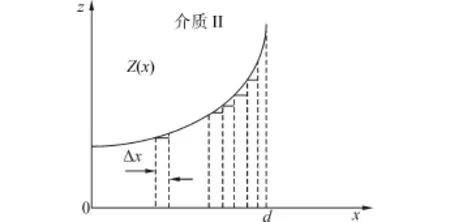
图1 介质阻抗梯度分布图Fig.1 The gradient change of acoustic impedance

设平面波从介质I垂直入射，经介质II，从介质III透射出，除介质III外所有介质中都有2个波，其中一个波向正x方向传播，另一个波向负x方向传播，在介质III中只有一个向正x方向传播的波。在阻抗梯度变化介质中阻抗是连续变化的，因此，为了便于计算需要进行离散化，将介质II分为N层，每层介质厚度为Δxi。需要注意的是，模型中介质II的阻抗是连续变化的，在离散后考虑到实际情况，每层介质中的阻抗、密度和声速也应当是变化的。为保证离散后介质模型的声学性能不发生改变，给出几点假设：1）声压和法向质点振速在每层介质的分界面上是连续的，即分界面两侧介质的声压和法向质点振速分别相等；2）介质II的左侧和右侧表面分别处于半无限空间中；3）为方便计算不考虑二次反射及多次反射的情况。

由理想流体媒质中小振幅声波运动方程可知：

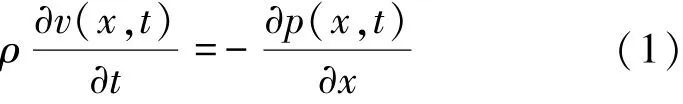
式中：p为介质质点的声压，v为介质质点的速度，ρ为密度。当考虑介质具有粘滞性时［13］，可以得到声压p、质点振速v与位移ξ的关系为

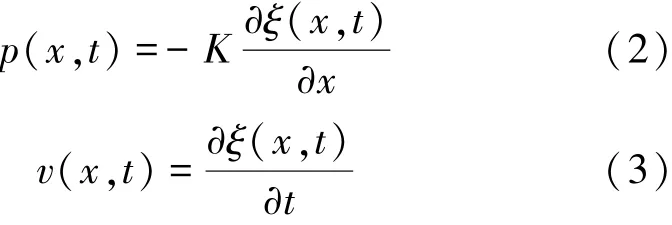
式中：K为复体积模量，表示为

式中：KS为体积弹性系数，η为粘滞系数。已知理想流体介质中一维波动方程的解为

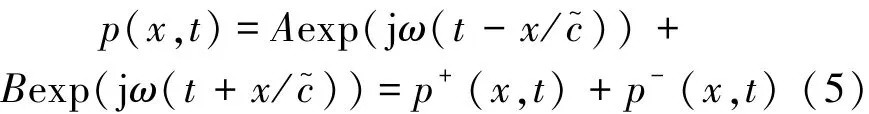
式中：c～为复声速，p＋（x，t）代表了沿正x方向行进的波，p－（x，t）代表了沿负x方向行进的波。定义声场中某位置的波阻抗Z（x）为

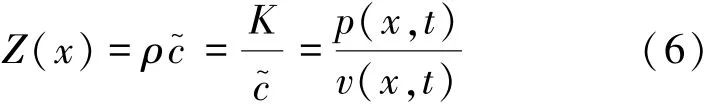
根据欧拉方程，式（5）可以得到质点振速为

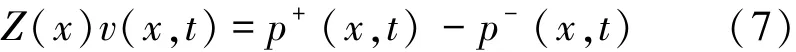
一维波动方程的解为关于时间的正弦函数，利用分离变量法，方程解写为

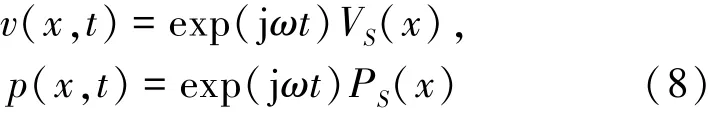
其中，

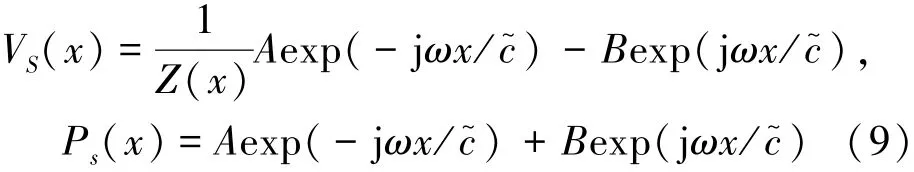
将式（8）中的v（x，t）代入式（1）中，由于分离变量后公式左右两侧都有时间因子，因此可以消去时间因子得到

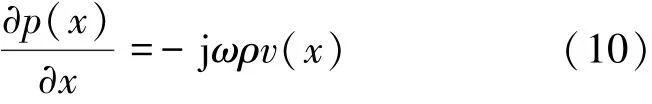
将式（5）和式（7）代入式（10）得到

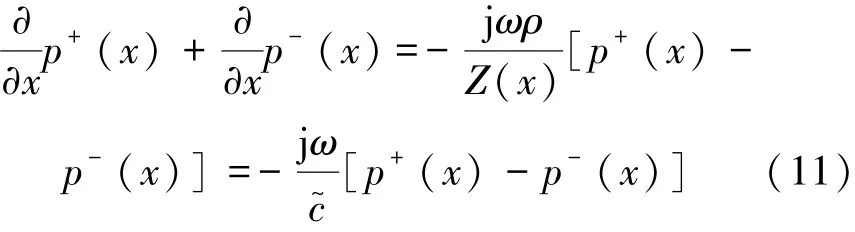
分别对式（2）和式（8）中的p（x，t）对t求偏导，联立式（3）可得

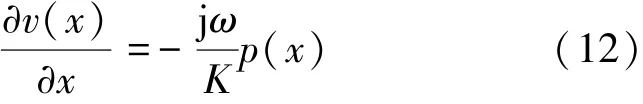
将式（5）和式（7）代入到式（12）中得到

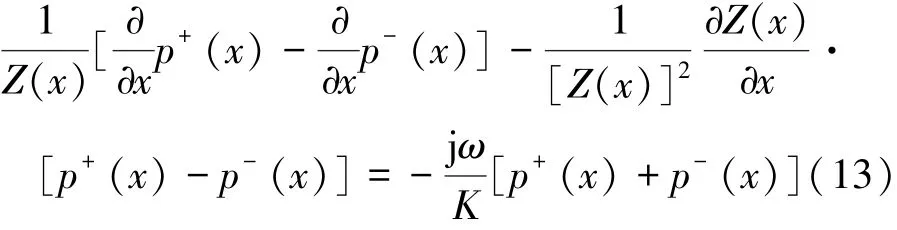
利用式（6），式（12）可简化为

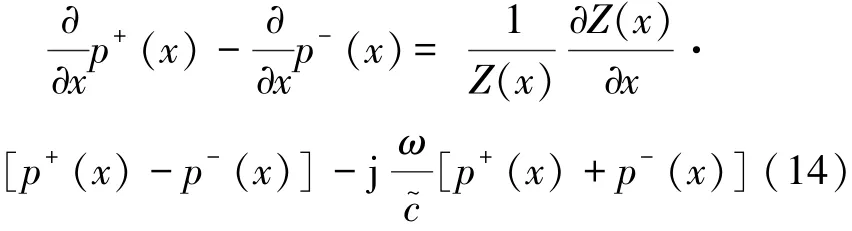
由式（11）与式（14），可分别得到

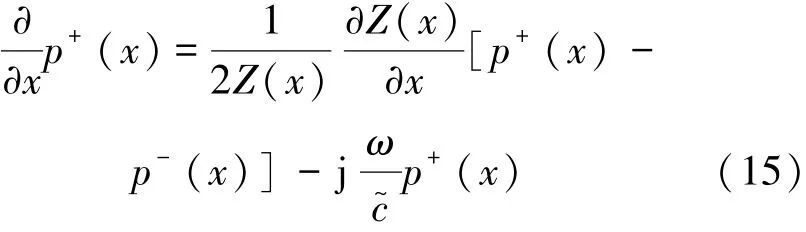
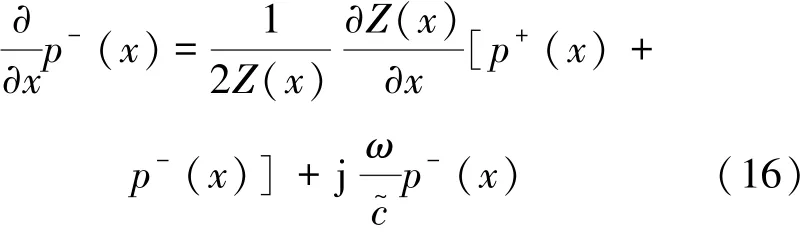
将式（5）写成向量的形式：

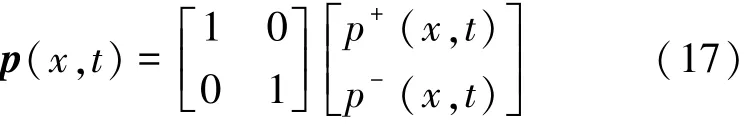
对式（17）求x偏导再代入式（15）和式（16），简化可以得到

式中：α（x）为介质阻抗的相对变化。

如果要求得微分方程式（18）的解，必须保证矩阵C（x）为常数，但在本模型中声速c和α（x）都是随x变化的，无法得到微分方程的解，因此必须对式（18）进行进一步变化。设声波透过阻抗梯度变化介质的总时间为T，考虑到声速不仅和传播距离x有关，而且还与传播时间t有关，因此可以进行变量替换，把C（x）转化为随时间t变化的函数。将式（18）变为

其中，当t＝0时，x＝0。

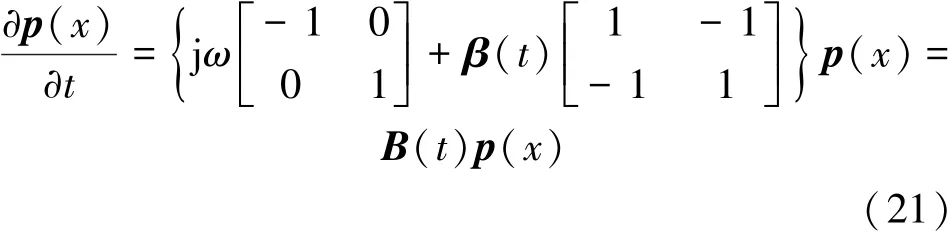
式中：

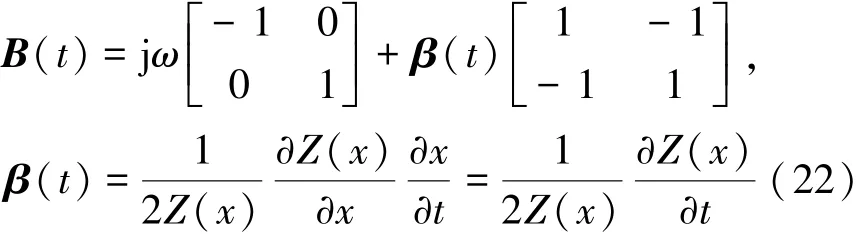
为求得微分方程式（21）的解，则β（t）一定为常数。当β（t）为常数时对式（22）积分，得到

式（23）说明，在本介质模型中为了保证式（21）有解，介质的阻抗应满足关于t的指数分布。而对于式（23）可以这样理解，即介质阻抗是密度和声速的乘积，而介质中的声速是关于声波传播时间t的函数，因此，也可以把介质阻抗看成是关于时间t的函数。

1.2 介质声学性能

设离散后介质II中任意一层介质分界面位置为x＝xM和x＝xN，xN－xM＝Δx，每层介质的入射声压和透射声压可以通过传递函数G（xM，xN）联系起来，即

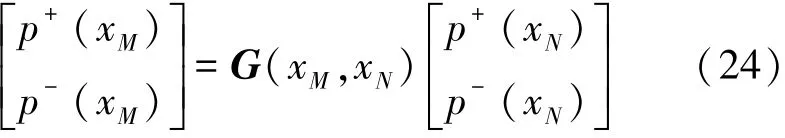
对于式（24）将xM用x代替，可以得到最为普遍的表达式为

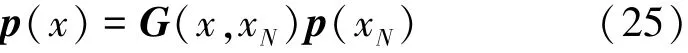
将式（25）对t求导可得

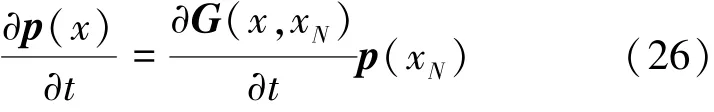
将式（25）代入式（21）中得到

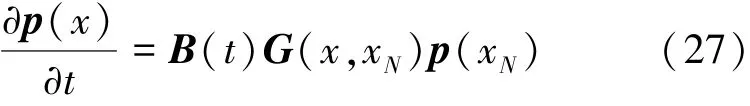
对比式（26）和（27）可以得到

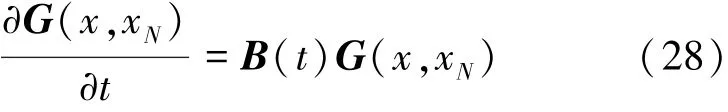
由1.1节内容可知，当介质阻抗为关于t的指数分布时微分方程有解，同理当介质阻抗为关于t的指数分布时上式的解可以表示为

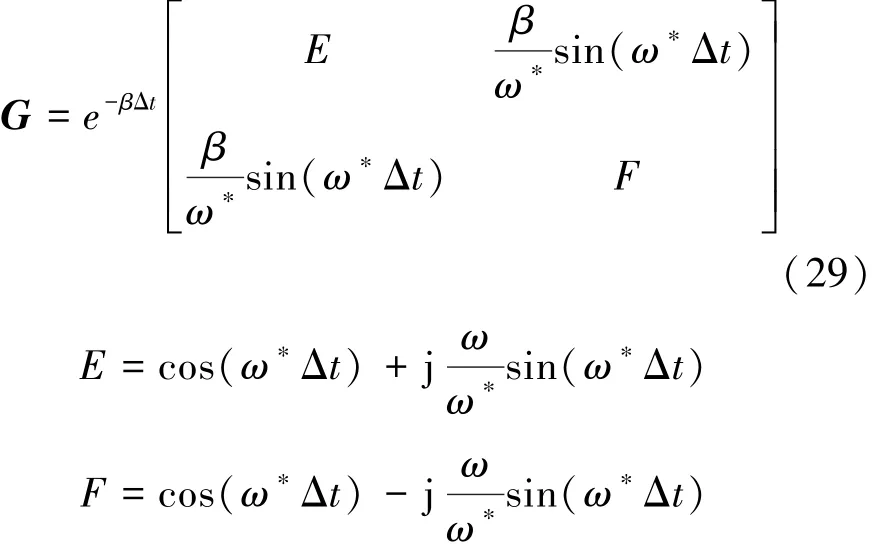
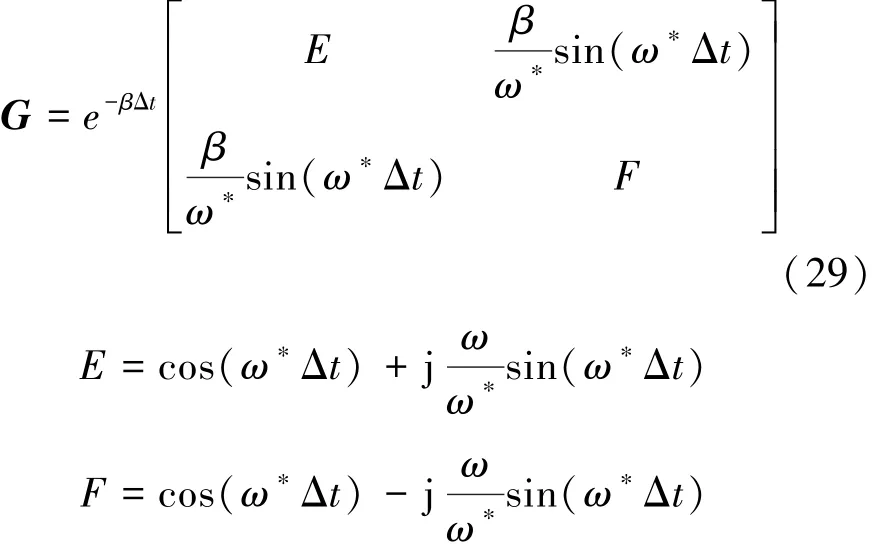
式中：ω*＝ω2－β2。介质II总传递函数Gtotal为

其中，Gn是第n层介质的传递函数。设介质中声速和密度也为关于t指数分布，即

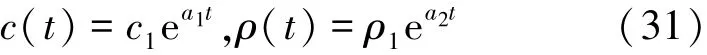
由式（31）可以得到

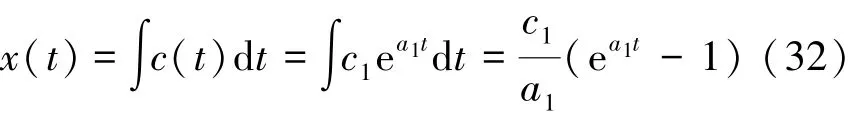
整理得到

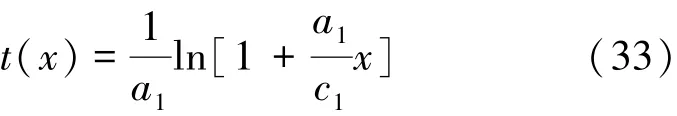
对于式（28），只有介质阻抗满足随指数分布时微分方程才有解，而对于阻抗为一般分布时，却不能得到解析解。为解决这一问题，使得任意阻抗分布也满足微分方程的条件，可以采用分段近似拟合的方法。该方法是将阻抗梯度变化介质分为N层，当N的取值足够大时，每层介质内的阻抗分布可由指数函数进行近似代替，并保证真实值与近似值的误差非常小，整个介质阻抗分布再由每层介质中的阻抗进行拟合。因此对于第n层介质，已知介质中任意两点的阻抗Z（xn）和Z（xn＋1），再根据式（23）就可以得到近似的指数函数为

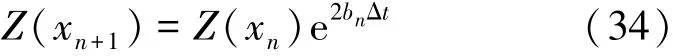
式中：bn为第n层介质中近似指数函数的系数，Δt为第n层及之内声波传播时间。整理得到bn为

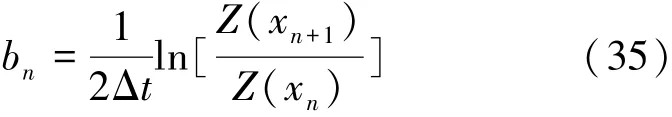
这样通过分段近似拟合，任意阻抗分布都满足式（27）微分方程解的存在条件，因此第n层介质的传递函数Gn表示为

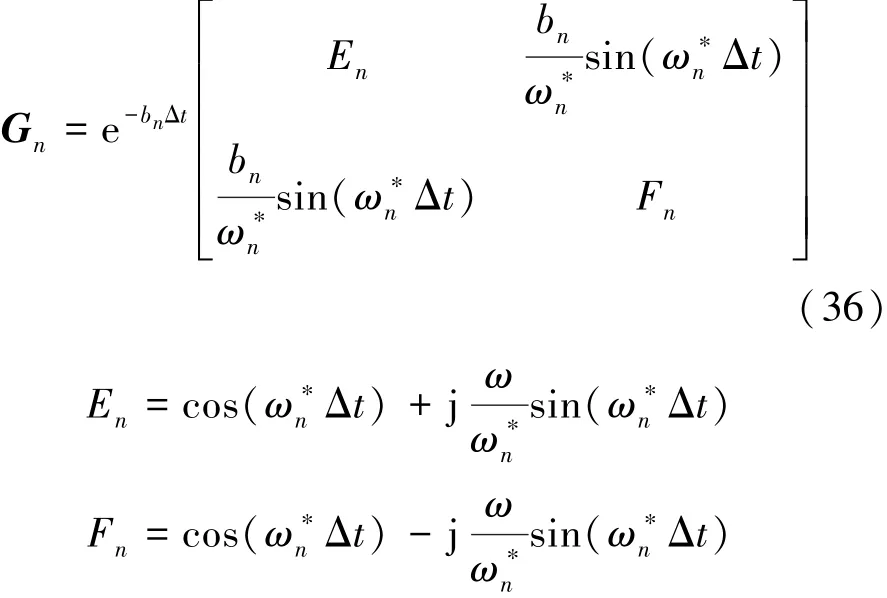
以上给出了每层介质中的传递函数，考虑到因为在介质III中只有一个透射整个层系而向正x方向传播的波，并且考虑梯度介质左右界面处的边界条件，可以得到

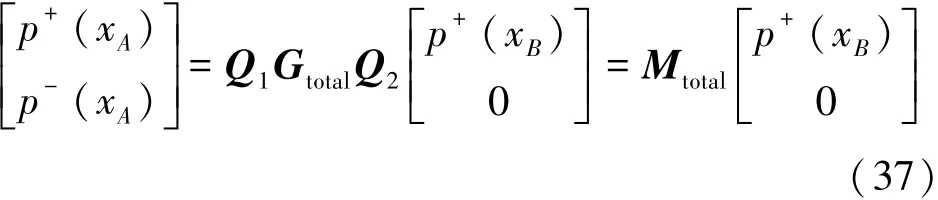
式中：Mtotal＝Q1GtotalQ2，Q1和Q2为

定义

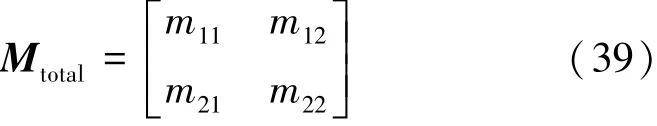
则介质II的透射系数和反射系数为

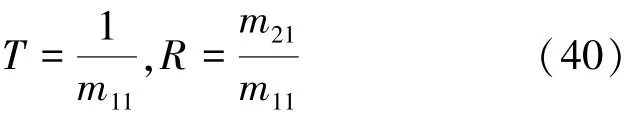
同样，可以得到整个介质II的反射系数为

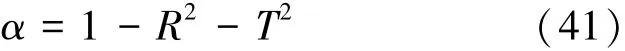
以上推导了阻抗梯度变化的非均匀介质中声传播特性公式。计算时首先确定声波通过介质的总时间，再求得每个时间点所对应的位置xn，然后计算每层介质中近似指数函数的系数bn和传递矩阵Gn，最终得到介质的反射系数和透声系数。

2 介质声学性能仿真

2.1 方法验证

利用Matlab软件编制程序进行数值仿真。设图1中的介质I为水，介质II为阻抗梯度变化的介质，介质III为钢板，钢板足够厚可以看成半无限空间，水的特性阻抗为Z1＝1.5×106kg／（s·m2），钢板的特性阻抗为Z3＝46.25×106kg／（s·m2）。将阻抗梯度变化介质结构与3种不同阻抗的均匀介质比较，对比其声学性能。设平面波垂直入射，介质的厚度d均为0.1 m，离散层数为200层，均匀介质分别选取为橡胶、环氧树脂和铅，阻抗分别为1.67×106kg／（s·m2）、3.2×106kg／（s·m2）和16.9×106kg／（s·m2）。已知介质II的阻抗分布满足指数分布：

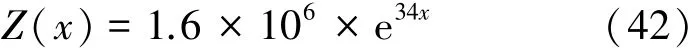
图2给出了4种介质的反射系数和吸声系数对比结果。可以看到，3种均匀介质的声学性能都具有频率选择性，声学性能曲线作振幅相等的周期振荡，而阻抗梯度变化介质的声学性能曲线并没有出现振荡现象。在低频段，阻抗梯度变化介质的声学性能曲线与4种介质的基本相同；在1～10 kHz频率范围内，随频率增加，阻抗梯度变化介质的反射系数单调递减至0.8，而吸声系数单调增大至0.4；在10 kHz以上的高频段，阻抗梯度变化介质的反射系数由0.8减小至0.2，反射系数要远小于均匀介质，而其吸声系数由0.4增大至0.9，吸声系数要远大于均匀介质，均好于3种均匀介质。分析原因：1）在低频段，声波波长远大于介质厚度，无论是均匀介质还是阻抗梯度变化介质，介质都如同“不存在”，因此低频段二者的声学性能基本相同；2）在中高频段，对于均匀介质，其阻抗接近于水的特性阻抗使得声波容易进入介质内，但在分界面处，钢板与均匀的特性阻抗相差很大，最大值达到30倍，此时声波将发生强烈反射。而对于阻抗梯度变化介质，它的表面阻抗接近于水的特性阻抗，有利于声波进入介质内部，在声波前进方向上，每一层的阻抗都比前一层略大一个微小量，起到阻抗过渡作用，并利用逐渐增大的阻抗对声波进行衰减，同时在分界面处，钢板与阻抗梯度变化介质的阻抗比值较小，仅为Z3／Z（0.1）≈1.1，能够对反射声波进行抑制，实现减少反射增加吸声的目的；3）阻抗梯度变化介质是由不同阻抗介质进行合理叠加而成，不同阻抗的介质能够在声学性能上形成互补，因此整体具有较宽的频带宽度。

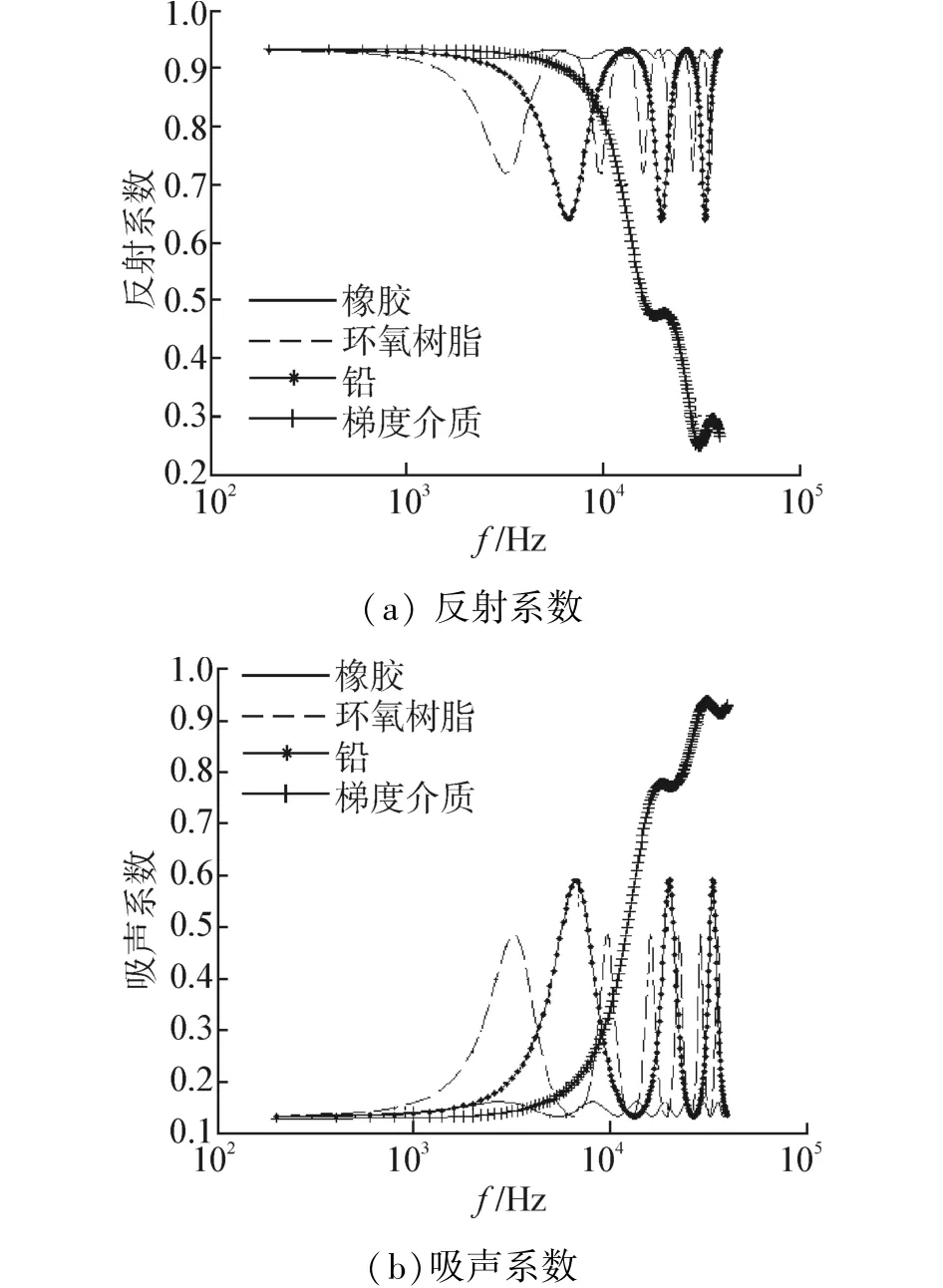
图2 Z3＝46×106kg／（s·m2）时4种介质声学性能对比Fig.2 Comparison of acoustic characteristics of four media when Z3＝46×106kg／（s·m2）

为验证模型的一般性，减小介质III的阻抗，使得Z3＝20×106kg／（s·m2），图3为4种介质对比结果。通过对比可以发现，均匀介质的透声面处的声波反射减小，吸声性能有所提高，但在中高频段阻抗梯度变化介质仍能够获得较小的反射系数和较大的吸声系数。总结以上结果表明：与传统均匀介质相比，在不增加吸声介质厚度的情况下，在中高频段阻抗梯度变化介质具有更低的反射系数和更大的吸声系数。

为了进一步验证算法的正确性，设阻抗梯度变化介质阻抗分布的阻抗变化率为0，此时分别采用分层介质传统算法和本文方法对同一均匀介质进行计算，结果如图4所示。从图中可知，当阻抗梯度变化介质的阻抗变化率为0时，阻抗梯度变化介质变为均匀介质，此时2种方法的计算结果是吻合的，这说明本文方法对于均匀介质也同样适用，能够验证本文算法的正确性。

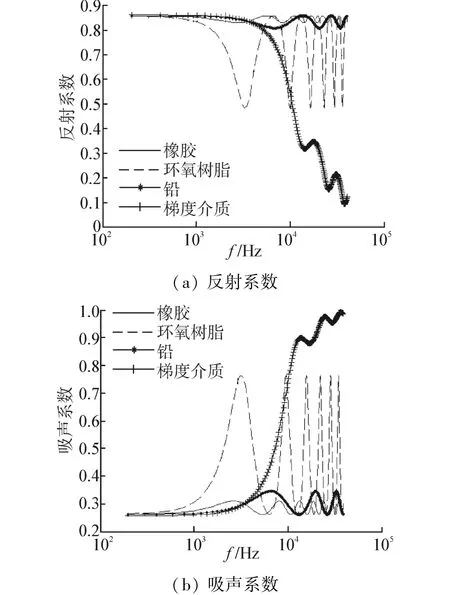
图3 Z3＝20×106kg／（s·m2）时4种介质声学性能对比Fig.3 Comparison of acoustic characteristics of four media when Z3＝20×106kg／（s·m2）

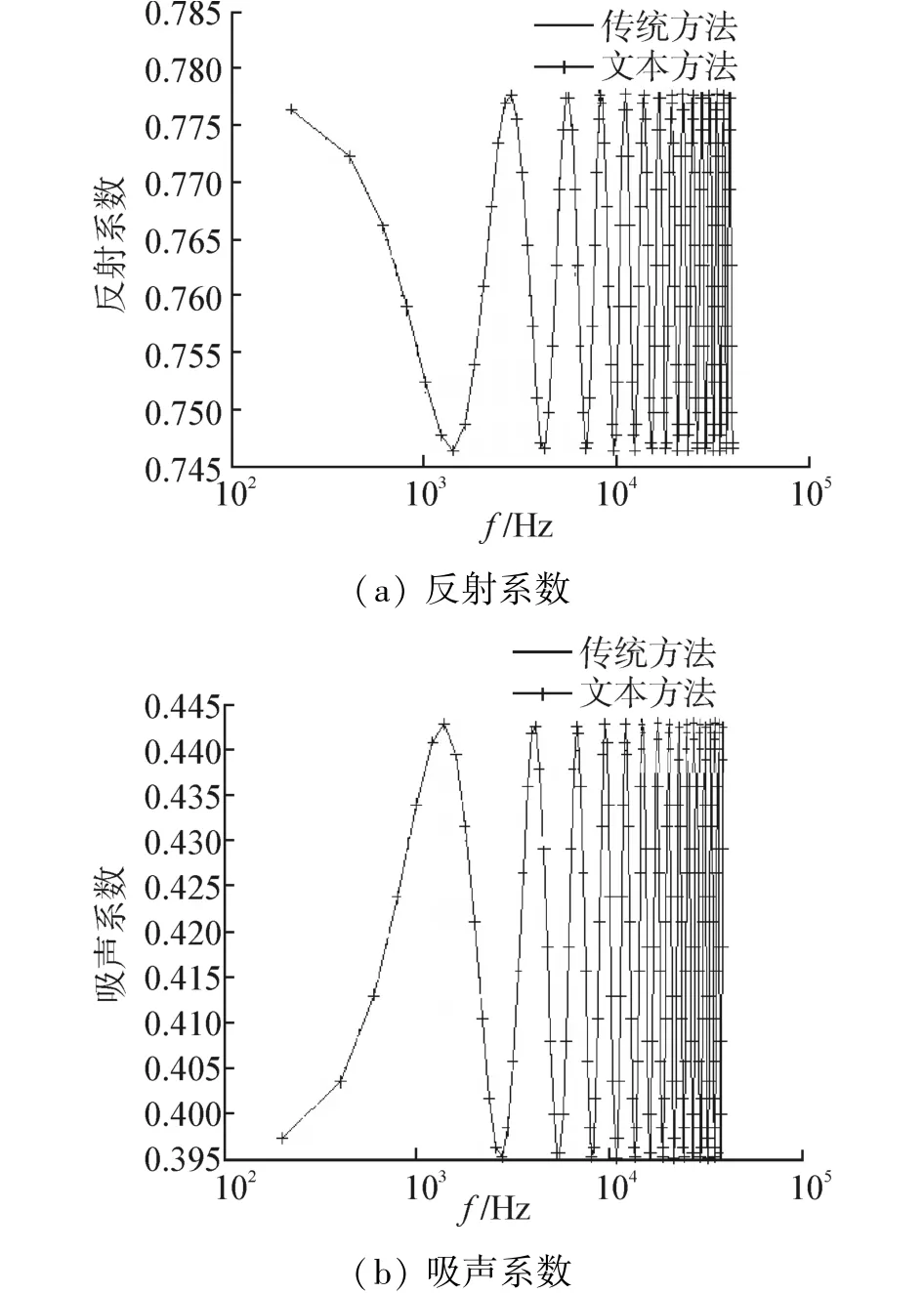
图4 传统方法和本文算法对比Fig.4 Comparison of traditional method and this method

2.2 介质层数影响

在离散计算中，为保证任意阻抗分布都能满足微分方程求解要求，需要保证N的取值足够大或每层介质厚度Δx足够小，使得每层介质阻抗分布可由指数分布近似，进而介质的总阻抗分布可由每层介质的阻抗拟合而成。这就引出人们最为关心的一个问题，即N选取为多大或每层介质厚度为多小时才能保证近似值与阻抗真实分布的误差足够小，不会影响介质的声传播规律和声学性能。以下对这一问题进行深入研究。

计算时首先将传播时间均匀分为N份，再计算每个时间间隔内介质的厚度Δxn，由于每层介质中声速是逐渐增大的，在相同时间间隔内所对应的Δxn值也是逐层增大的，如果采用分析每层介质厚度与波长比的方法将无法对其变化影响进行有效说明，因此这里考虑介质层数N的选取问题。图5给出了N变化对介质声学性能的影响。可以看到，当N＜100时反射系数曲线和吸声系数曲线有明显的变化；当N＞100时反射系数和吸声系数曲线非常平坦，介质层数N由100增大到200时，介质的反射系数仅发生了0.005的变化。

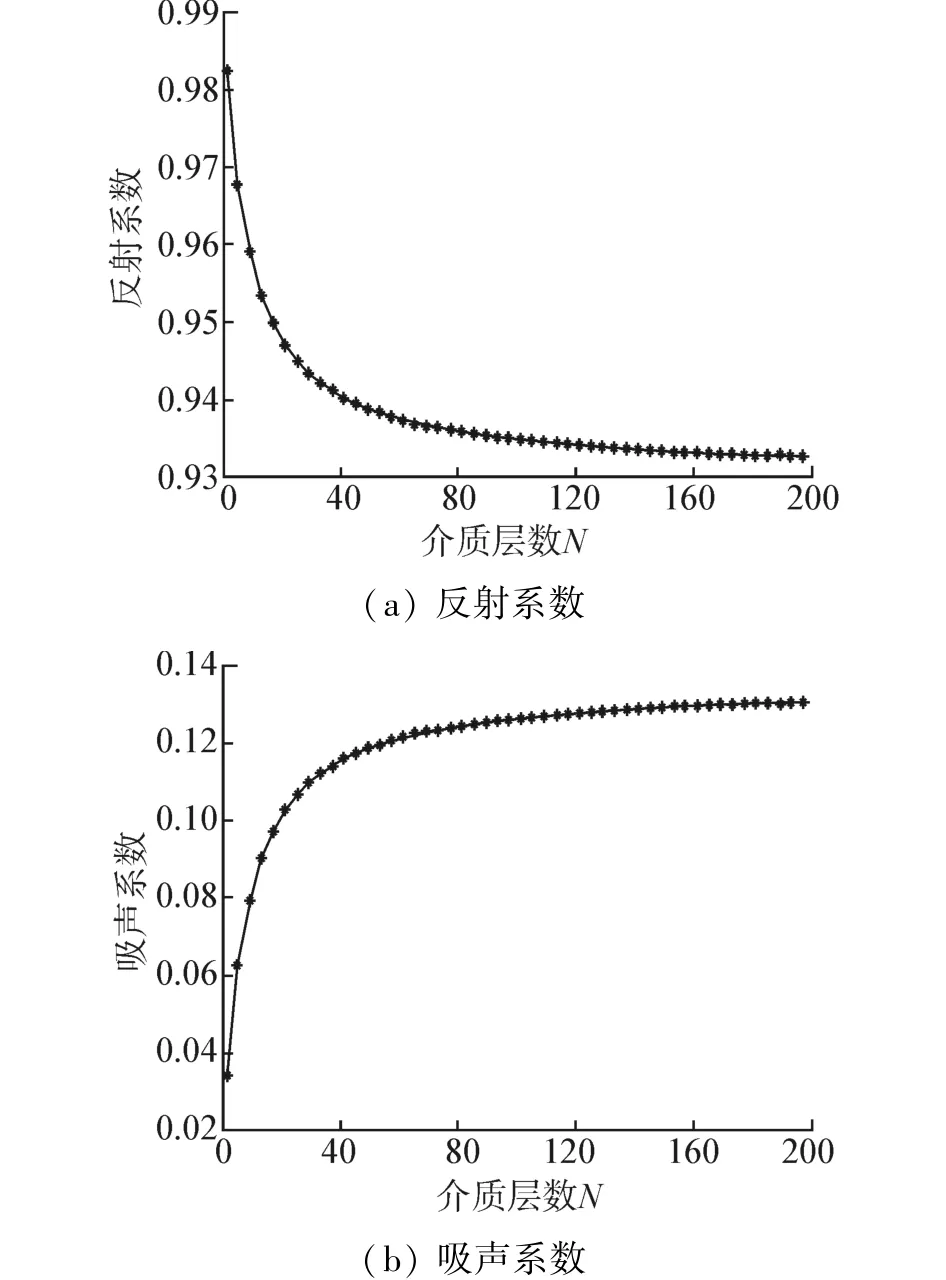
图5 介质层数对介质声学性能影响Fig.5 The relationship between N and acoustic characteristics of media

这说明：当N＞100时指数近似的结果与实际阻抗分布之间的误差已经很小，对介质的声学性能影响也很小，此时N的选择能够满足模型假设条件中足够大的要求，介质的阻抗分布可由每层介质的阻抗近似拟合而成。

3 实验研究与分析

为验证理论和仿真研究的正确性，设计制作了阻抗梯度变化介质实验样品，采用脉冲声管法对介质的水下声学性能进行测量。

3.1 实验介质的制备

首先，基于沉降法理论制备了阻抗梯度变化实验介质。制备装置主要包括：沉降玻璃管、沉降模具、干燥箱、万能拉伸试验机、保温箱、混合器皿，选用铝粉和铁粉作为制备材料。具体制备步骤如下：1）将沉降玻璃管和沉降模具内表面擦洗干净，并在沉降模具上均匀涂抹适量的脱模剂；2）称量待包覆粉末和高分子粘结剂，高分子粘结剂为酚醛树脂与乌洛托品的混合物；3）使粉末与粘结剂混合均匀，再将混料容器加热继续热混；4）将包裹粉末迅速置入有机玻璃管中，管中盛满水，粉末进行自然沉降，待粉末完全沉降后，将沉降管中的水排出；5）将沉降模具和沉积粉末置于干燥箱中进行干燥处理；6）将干燥后模具置于万能拉伸试验机下进行压制，压制出相应厚度；7）将模具固定后，放入保温箱中在200℃下进行固化处理。制备后的阻抗梯度变化介质实物如图6所示。

需要说明的是，本文目前掌握的制备技术和知识水平，很难解决由于材料互溶性不好导致固化后介质非常脆、容易断裂的问题。因此，在制作时综合考虑材料之间的互溶性、材料的阻抗差异、固化效果、硬度等因素，在保证介质阻抗连续变化的前提条件下提高了介质迎声面的阻抗值，制作完毕后对介质的阻抗进行测量，介质的阻抗分布情况如图7所示。可以看到，制备的实验介质的阻抗值在6.3×106～16.05×106kg／（s·m2）范围之间，介质具有明显的梯度分布，随着距离的增加介质阻抗分布并没有出现突变，基本上呈连续变化，能够满足实验要求。

图6 制备的阻抗梯度变化介质Fig.6 The media with gradient change of impedance

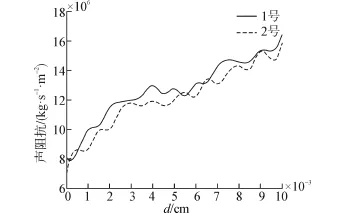
图7 介质的阻抗分布Fig.7 Acoustic impedance value of media

3.2 实验数据处理

依据国家标准GB／T14369-93，采用脉冲声管法对介质的水下声学性能进行测量。整个测试系统由脉冲声管、收发换能器、信号源、B＆K2713功率放大器、收发转换装置、B＆K2636测量放大器、B＆K1617带通滤波器和示波器组成，实验测量系统如图8所示。脉冲声管的声硬末端采用大质量的圆形钢块，钢块厚度为5 cm，直径为5.7 cm；选用聚氨酯作为对比样品，直径为5.6 cm，厚度为1 cm，梯度介质的厚度为1 cm。介质的特点，将制备的1号阻抗梯度变化介质与相同厚度的聚氨酯均匀介质相比较，对比结果如图9所示。

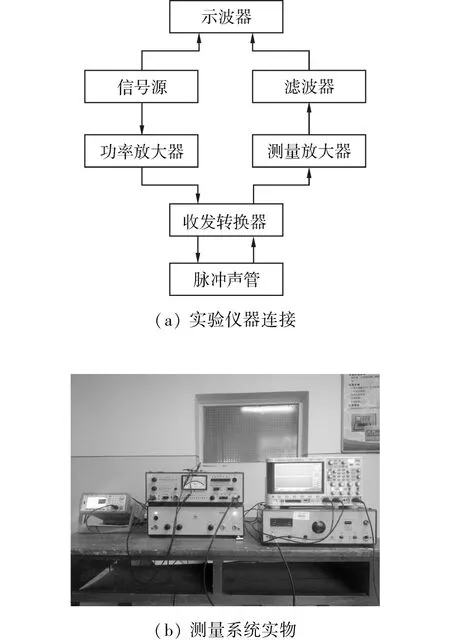
图8 实验测量系统Fig.8 Experimental measurement system

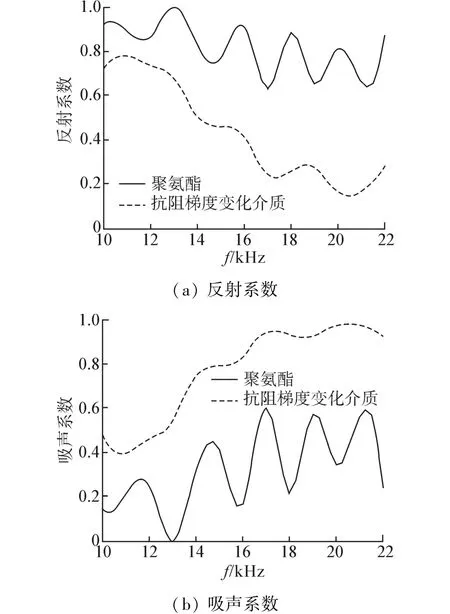
图9 1号梯度介质与聚氨酯对比结果Fig.9 Comparison of No.1 media and polyurethane

在图9中，阻抗梯度变化介质与阻抗均匀分布的聚氨酯的声学性能有很大不同，聚氨酯的声学性能曲线呈周期振荡，反射系数在0.65～0.95内波动变化，吸声系数0.1～0.58内波动变化；与聚氨酯相比，在低频段阻抗梯度变化介质的反射系数更小，吸声系数更大，并且反射系数随频率的增大而减小，吸声系数随频率的增大而增大，这与仿真结果得到的规律是相同的。值得注意的是，图中阻抗梯度变化介质的声学性能曲线的变化规律并没有仿真结果给出的那么理想，曲线中会出现不规则的凹陷和凸起，分析原因，这可能是因为仿真模型是建立在阻抗连续变化的基础上的，而在样品介质制备过程中，由于制备工艺的原因会存在阻抗局部连续性不好的问题，此外实验测量中某些频率下反射波波形很不稳定，信号幅值的读取也会带来误差。

图10为2号阻抗梯度变化介质与聚氨酯的测量结果。可以看到，图10的实验结果与图9中具有很好的一致性，虽然阻抗梯度变化介质的阻抗分布发生了变化，但与均匀聚氨酯介质相比，阻抗梯度变化介质仍然获得更小的反射系数，更大的吸声系数，得到的实验规律与仿真结果相同。以上结果表明，在不增加介质厚度的情况下，与传统均匀介质相比，阻抗梯度变化介质具有更大的中高频吸声特性。

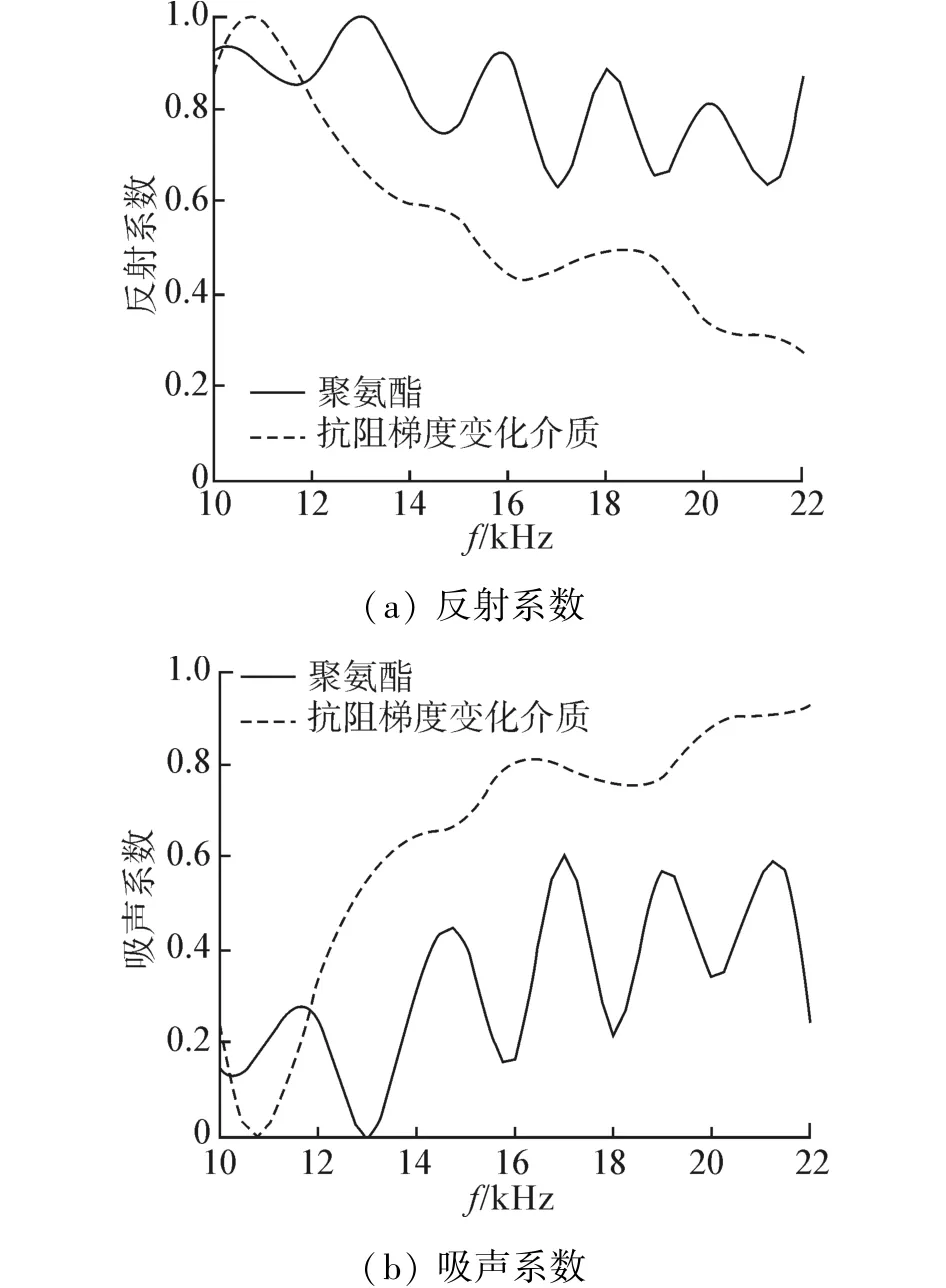
图10 2号介质与聚氨酯对比结果Fig.10 Comparison of No.2 gradient media and polyurethane

4 结束语

本文对阻抗梯度变化介质的声学性能进行了研究，建立了阻抗连续梯度变化介质中声波传播模型，推导了阻抗任意分布条件下介质中声学性能公式。通过数值仿真在多种条件下验证了本文方法，制备了阻抗梯度变化介质，对介质的阻抗分布情况进行了测量，进行了水中阻抗梯度变化介质的声学性能测量实验。研究发现：

1）在不增加吸声介质厚度的情况下，在中高频段阻抗连续梯度变化介质具有更小反射系数和更大的吸声系数；

2）当N＞100时，介质层数能够满足模型假设条件中足够大的要求，以保证阻抗变化的连续性；

3）制备的阻抗梯度变化介质能够满足实验要求，证明了本文方法的可行性，实验结果验证了理论研究的正确性。

可以说本文的研究为阻抗梯度变化介质在实际工程中的应用提供了理论依据和实践基础，对水下减振降噪具有比较积极的意义。

参考文献：

［1］刘志宏，盛美萍.水下多层均匀材料垂直入射的声特性分析［J］.噪声与振动控制，2005，4（2）：11-13.LIU Zhihong，SHENG Meiping.Analysis of sound characteristics of a normal incidence plane wave on isotropic symmetric plate in water［J］.Noise and Vibration Control，2005，4（2）：11-13.

［2］李海涛，朱锡，王林，等.水下均匀复合层结构的声特性研究［J］.武汉理工大学学报，2008，30（6）：105-109.LI Haitao，ZHU Xi，WANG Lin，et al.Investigation of sound field in homogeneous multiple-layer structures in water［J］.Journal of Wuhan University of Technology，2008，30（6）：105-109.

［3］BERETTI S，VASSAS M.Multifunction coating and enhanced anechoic coating by using multi-layer optimization［C］／／Conference Proceedings of UDT.London，1996：300-303.

［4］EMERY P A.New cladding material［C］／／Conference Proceedings of UDT.London，1995：527-531.

［5］PEPLOW A.Acoustic propagation in variable sound speed profiles［C］／／8th European Conference on Noise Control.Edinburgh，Scotland，2009：302-307.

［6］何祚镛，王曼.水下均匀材料复合层吸声特性研究［J］.应用声学，1996，15（5）：6-11.HE Zuoyong，WANG Man.Investigation of the sound absorption of homogeneous composite multiple-layer structures in water［J］.Applied Acoustics，1996，15（5）：6-11.

［7］何祚镛，王曼.水下非均匀复合层结构吸声的理论研究［J］.应用声学，1996，15（5）：12-19.HE Zuoyong，WANG Man.Investigation of the sound absorption of non-homogeneous composite multiple-layer structures in water［J］.Applied Acoustics，1996，15（5）：12-19.

［8］朱金华，刘巨斌，姚树人，等.分层高分子介质中的声吸收［J］.高分子材料科学与工程，2001，17（3）：34-38.ZHU Jinhua，LIU Jubin，YAO Shuren，et al.The acoustic absorption in layered polymer materials［J］.Polymer Materials Science and Engineering，2001，17（3）：34-38.

［9］杨雪，王源升，朱金华，等.梯度聚氨酯水声吸声性能的研究［J］.高分子材料科学与工程，2007，23（1）：169-172.YANG Xue，WANG Yuansheng，ZHU Jinhua，et al.Study on the underwater sound absorption properties of gradient polyurethanes［J］.Polymer Materials Science and Engineering，2007，23（1）：169-172.

［10］杨雪，王源升，余红伟.梯度聚氨酯吸声性能研究［J］.武汉理工大学学报，2008，30（3）：21-23.YANG Xue，WANG Yuansheng，YU Hongwei.Research on sound absorption properties of graded polyurethanes［J］.Journal of Wuhan University of Technology，2008，30（3）：21-23.

［11］王源升，杨雪，朱金华，等.水溶性高分子梯度溶液吸声机理的研究［J］.声学学报，2006，31（1）：14-18.WANG Yuansheng，YANG Xue，ZHU Jinhua，et al.Study on the sound absorption mechanism in gradient water-soluble polymer solution［J］.Acta Acustica，2006，31（1）：14-18.

［12］王源升，杨雪，朱金华，等.梯度高分子溶液的声衰减［J］.高分子材料科学与工程，2005，21（5）：129-132.WANG Yuansheng，YANG Xue，ZHU Jinhua，et al.The underwater sound attenuation of gradient polymer solutions［J］.Polymer Materials Science and Engineering，2005，21（5）：129-132.

［13］杜功焕，朱哲民，龚秀芬.声学基础［M］.南京：南京大学出版社，2010：169-172.

Acoustic characteristics of the media with gradient change of impedance

YANG Desen，SUN Yu，HU Bo，HAN Chuang，JIN Shiyuan
（Science and Technology on Underwater Acoustic Laboratory，Harbin Engineering University，Harbin 150001，China）

The media with gradient change of impedance is an acoustic media which is developed from multiple layer media.Using the principle of impedance matching method，better acoustic properties based on the media with gradient change of impedance with different characteristic impedance of materials can be obtained.Applying this media to underwater acoustic engineering，the model of acoustic propagation in the media was established and the sound properties were investigated.The calculation formulas for the reflection and sound absorption coefficients of the media with gradient change of impedance were derived.Numerical simulations were also conducted.The acoustic properties of the media with gradient change of impedance were compared with traditional homogeneous media.The rules of the number of layers were discussed.The media with gradient change of impedance were prepared and the experiments in a pulse acoustic tube were carried out.The experimental results showed that the preparation media with continuous distribution of impedance can meet the need of experiment.The measure results verified smaller reflection coefficient and larger absorption coefficient of the media with gradient change of impedance，which provide a theoretical basis for the application of the media with gradient change of impedance in acoustic engineering.

acoustic impedance；gradient change；acoustic characteristic；reflection coefficient；impedance matching；acoustic media

10.3969／j.issn.1006-7043.201401002

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006－7043.201401002.html

TB535

A

1006-7043（2014）12-1458-09

2014-01-02.网络出版时间：2014-12-02.

长江学者和创新团队发展计划资助项目（IRT1228）；国家自然科学基金资助项目（11204049，11204050）；高等学校博士学科点专项科研基金资助项目（20122304120023）.

杨德森（1957-），男，教授，博士生导师；胡博（1980-），男，副研究员.

胡博，E-mail：kidd1105＠sina.com.