对数域的光学相干层析图像噪声模型分析

纪 文，孙水发，王 帅，董方敏

（三峡大学智能视觉与图像信息研究所，宜昌443002）

对数域的光学相干层析图像噪声模型分析

纪 文，孙水发*，王 帅，董方敏

（三峡大学智能视觉与图像信息研究所，宜昌443002）

为了分析光学相干层析成像技术（OCT）的图像对数变换前后的斑点噪声分布模型，为图像去噪及其它图像处理过程提供参考，采用了先推导斑点噪声理论分布模型，再通过实验数据验证的方法。首先分析了对数变换前斑点噪声的统计特性，利用数学理论推导得到斑点噪声对数变换后的理论分布模型，然后用OCT心血管图像的平滑区域作为噪声的试验数据，得到变换前后斑点噪声的直方图分布数据，最后用理论分布模型对试验数据进行曲线拟合，取得了确定系数、均方根差和卡方检测的评价数据。结果表明，对数变换后斑点噪声分布符合Fisher-Tippett分布。这一结果对OCT图像去噪等处理过程是有帮助的。

图像处理；噪声模型；对数变换；光学相干层析图像；斑点噪声

引 言

上个世纪末期，随着宽带光源的实用化，光学相干层析（optical coherence tomography，OCT）成像技术得到极大地发展［1-3］，因其低侵入性、高分辨率的特性成为临床上的技术热点［4］。但是OCT图像中存在的斑点噪声影响了该技术的广泛使用。在OCT成像系统中，斑点噪声本质上也是由光的干涉引起的，样品光会因为样品内部含有大量的散射颗粒而形成复杂的多次后向散射，因此反射光波前形成畸变，在与参考光干涉之后形成的图像便会有大量的斑点噪声［5］，它实质上也是检测目标的信息载体［6］。而关于干涉成像的噪声分析，人们已经做了很多研究，并建立起了关于斑点噪声的统计分布模型［7-9］。参考文献［7］中分析了斑点噪声的分布模型，提出强度服从负指数分布，幅度服从瑞利分布的结论。参考文献［9］中对幅度服从瑞利分布做了进一步的研究，并做了证明。

OCT图像中的斑点噪声一般被认为是乘性噪声模型，然而在去噪和重建方面很多现行的算法都是基于加性噪声的，并且在成像和视觉系统中加性噪声也是最常见的。为了利用这些去噪算法以及噪声模型，通过对数变换将乘性噪声转化为加性噪声，成为OCT图像去噪中必不可少的步骤之一。对数变换作为一种非线性变换，使得转换之后的斑点噪声的统计特性也相应的发生了变化。参考文献［10］中对合成孔径雷达图像的斑点噪声及其对数变换之后的分布模型进行了研究，考虑到OCT图像与合成孔径雷达图像成像原理的类似性，借助这篇文章的思路，作者对OCT图像斑点噪声对数变换前后的分布模型从理论和实验两方面进行了研究。先回顾了斑点噪声的统计特性，然后通过数学推导得到对数变换之后的分布模型；并通过试验验证推导出的数学模型，可知，对数变换后噪声分布符合Fisher-Tippett（F-T）分布。

1 斑点噪声统计特性

在OCT成像系统中，样品光在样品中经过复杂的多次后向散射，再与参考光相干涉之后便会形成大量斑点噪声［11-12］。对于OCT系统接收的回波信号，可以看作是多个回波的叠加，回波具有Akeiθk形式，那么接收传感器得到总的回波信号也可以写为：

式中，Akeiθk表示第k个散射点的回波，Ak和θk分别表示其幅度和相位，A和θ分别表示总回波信号的幅度和相位，M表示散射点的总个数。总的回波信号也可以用一个复数Z＝Ar＋j Ai＝A cosθ＋j A sinθ来表示。当M的值比较大时，根据中心极限定理知Ar和Ai两者都可近似为均值为0，标准差σ为正态分布，据此可以求得回波信号幅度的概率密度函数为：

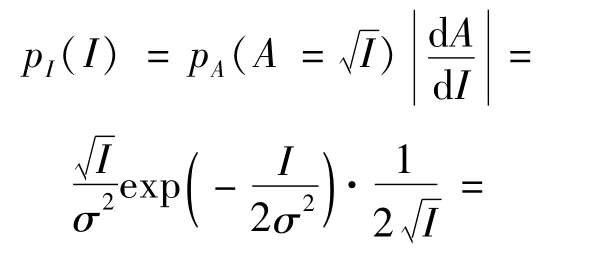
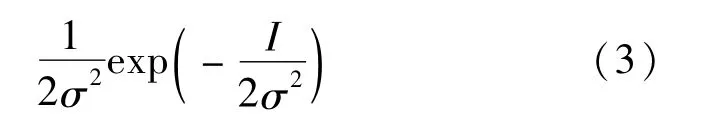
则其均值为E（I）＝σ2，方差为v（I）＝σ4。

2 对数域斑点噪声统计模型

对数变换是一种非线性变换，它会使得斑点噪声的统计特性发生变化，因此下面分析对数域下的斑点噪声分布模型。根据参考文献［13］和参考文献［14］，知道OCT图像中斑点噪声为乘性噪声，设其噪声模型为：

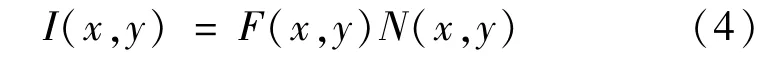
式中，I（x，y）为OCT图像的观察值，F（x，y）是图像没有噪声的期望值，N（x，y）是斑点噪声。对（4）式两边同时取对数得：

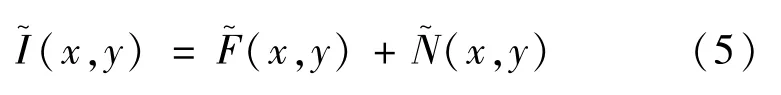
假设：

式中，α和β为系数。那么N～的概率密度函数为：

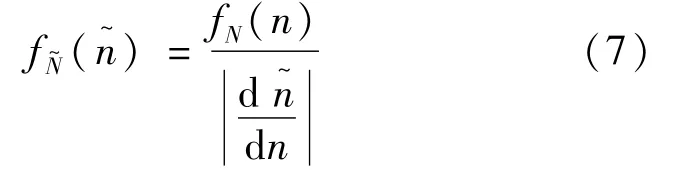
整理得：

式中，γ表示欧拉常数［15］，γ＝0.5772。

3 实验证明

为了验证上述分析，下面用实验进行验证。在1幅OCT心血管图上选择6个平滑区域作为原始噪声数据，对选择区域对数变换前后的分布模型中的感兴趣区域（regions of inferest，ROI）进行实验分析，如图1所示。

图1由频域系统平台得到［16］。该系统利用的是半峰全宽为25nm、输出功率为1.4W、脉冲时间为80fs的光源，光源被一个2×2的耦合器以1∶9分为两份。两束光经参考臂和样品臂反射回来后发生干涉，系统使用区域扫描相机代替传统的线扫描相机记录OCT谱，得到OCT图像。

Fig.1 ROIof OCT images

3.1 对数变换前后噪声的统计模型变化及分析

图2对数变换前后感兴趣区域图像信号的统计分布情况，带方格的曲线表示变换前，带圆点的曲线表示变换后的信号统计分布。

将选择的平滑区域作为噪声，统计出选择区域的直方图，并用曲线来绘制，图2显示了图1中6个区域的直方图曲线以及对数变换后的直方图曲线。图中带方格的曲线表示变换前的直方图，由于选择的区域是平滑区域，像素灰度值较低且比较集中，灰度较高的像素点较少，画出的直方图不够直观，所以把选择区域的数据进行了归一化处理。尽管不是十分明显，也可以发现变换前的直方图曲线右侧拖尾比左侧长。带圆圈的曲线表示对数变换之后的直方图曲线，由于变换之后的像素值也比较小，且十分集中，于是把变换之后的数据也进行了归一化处理。从图中不难发现带圆圈的曲线左侧有很长的拖尾，右侧却几乎没有拖尾，这是Fisher-Tippett分布的重要特征之一。

3.2 对数变换后噪声模型分析

3.2.1 曲线拟合 利用Fisher-Tippett分布函数和高斯分布函数对6个选区变换后的直方图曲线进行拟合。

图3对应图1中6个所选区域，点状对应选择区域变换后的直方图数据，使用F-T函数曲线f（x）＝exp［b（x－a）］exp｛－exp［d（x－c）］／2｝来对数据进行曲线拟合（其中，a，b，c，d为系数），利用最小二乘法得到公式中的参量，结果见表1，将得到的参量代入曲线方程，并将拟合曲线绘制在图中（图中实线表示），不难发现，拟合曲线恰巧穿过大量的数据点，且走势与数据点分布走势有很强的相似性，说明拟合曲线对数据的拟合效果比较好。

使用高斯函数f（x）＝a exp［－（x－b）2／c2］对数据进行拟合，得出的方程参量见表2，图中带有方格的曲线代表高斯拟合曲线。不难发现，该曲线走势与数据点分布走势有一定的相似性，但是大部分数据点分布在曲线的两侧，甚至与该曲线偏离很多。这说明高斯拟合曲线对数据的拟合效果较差。

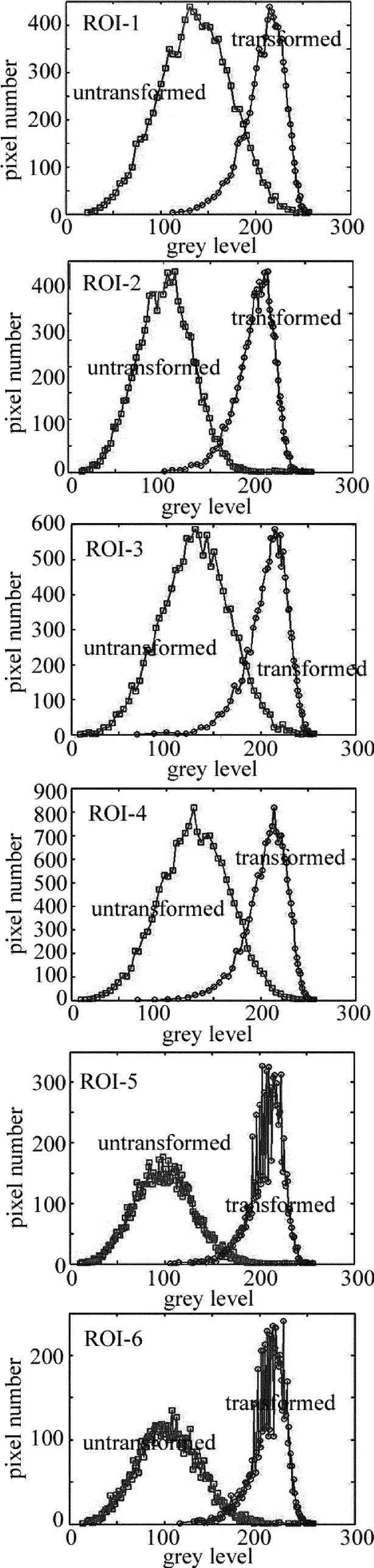
Fig.2 Distributions of six ROIs before and after the logarithm transformation of Fig.1

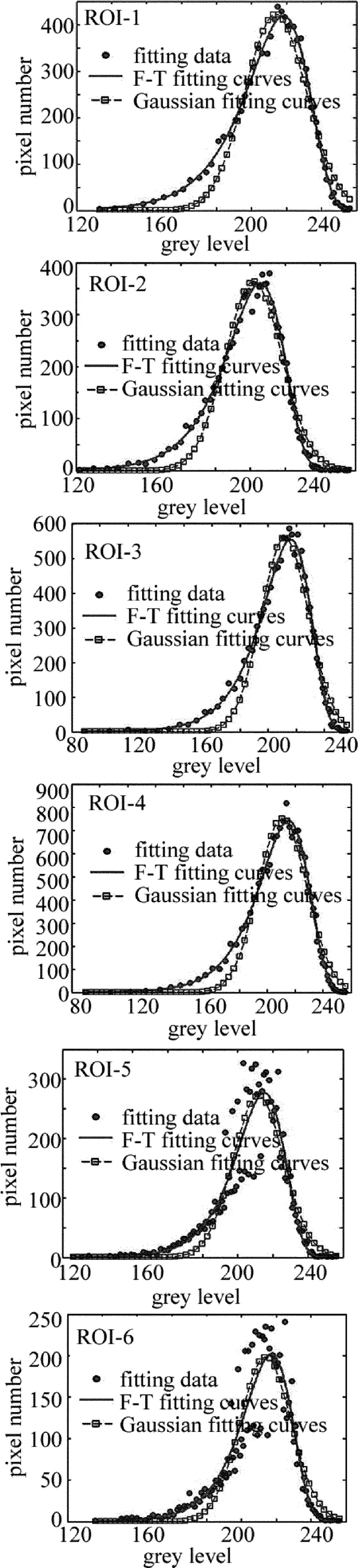
Fig.3 Fitting curve of six ROIs of Fig.1

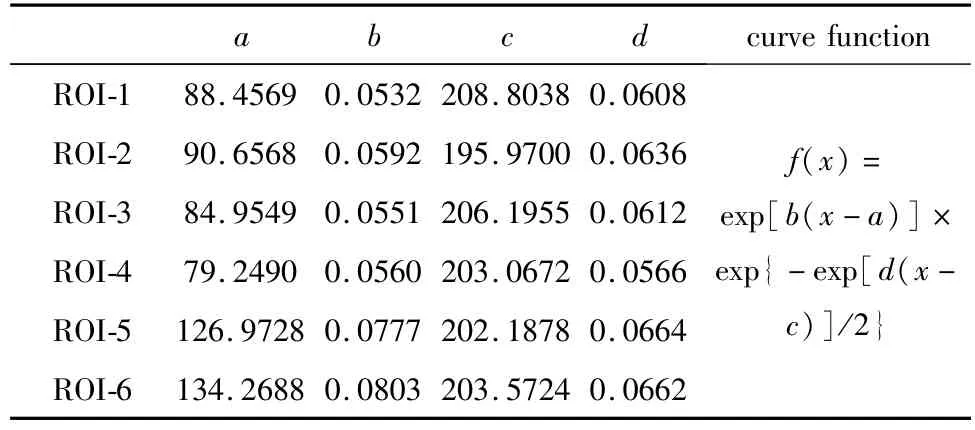
Table 1 Estimated parameters of F-T distribution function of Fig.1

Table 2 Estimated parameters of Gaussian distribution function of Fig.1

3.2.2 拟合性能分析 为了对拟合的效果进行评估，用确定系数（R-square）、均方根差（root mean square error，RMSE）和卡方（X2）检测评价拟合效果。R-square称为曲线方程的确定系数，范围在0～1之间，越接近1，表明曲线对数据的拟合效果越好。均方根也称回归系统的拟合标准差，它是拟合数据和原始数据的“和方差”取均值并开方得到的，该值越小说明拟合出的数据越是接近原始数据，假设模型的拟合效果越好。卡方检验法是在总体X的分布未知时，先对数据分布进行假设，然后根据样本的经验分布和所假设的理论分布之间的吻合程度来决定是否接受原假设的一种检测方法，它也是拟合度检验的重要方式之一。

通过观察表3、表4和表5不难发现，6个区域的F-T分布的RMSE检测结果和X2检测结果都小于高斯分布的检测结果，而对应的R-square检测结果较大，这证明F-T分布曲线对变换后的直方图曲线拟合更精确。

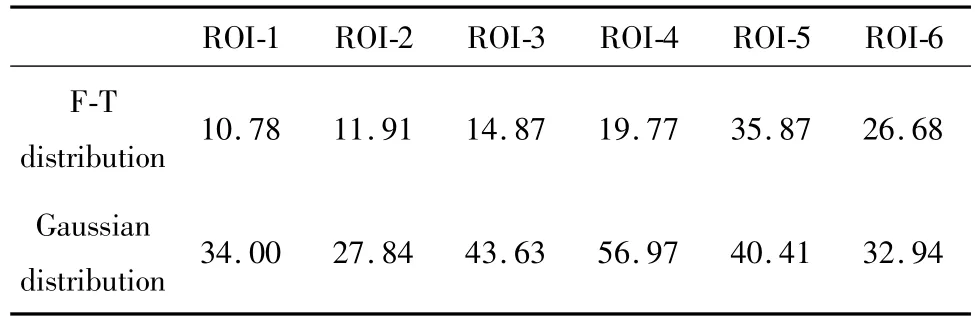
Table 3 RMSE testing results of Fig.1

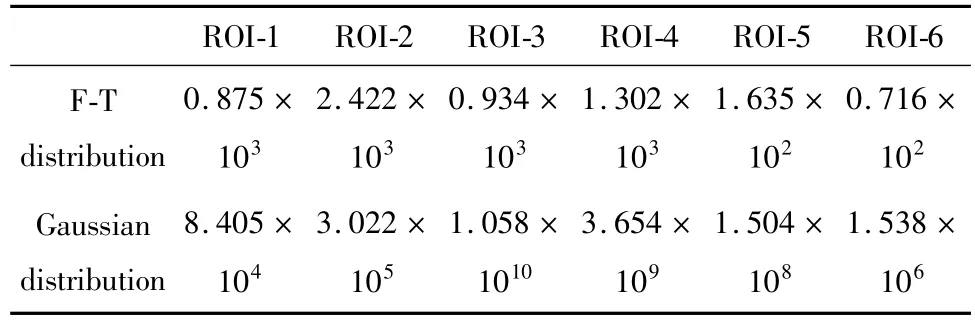
Table 4 X2testing results of Fig.1

Table 5 R-square testing results of Fig.1

3.3 更多图像的实验

为了进一步证明理论推导的可靠性，选择在更多OCT图像进行实验验证，如图4所示，选择两幅心血管OCT图像，该图也是由频域OCT系统平台产生。在两幅图像中，分别选择两个平滑区域做对数变换，为了增加实验的可对比性，不仅使用了Fisher-Tippett分布曲线和单高斯分布曲线（sigle Gaussian model，SGM）进行拟合，还使用了混合高斯分布（Gaussian mixfure model，GMM）进行拟合。文中使用了k＝2的混合高斯分布，理论上，随着k的增加，混合高斯可以拟合任意形状的数据，但是当k过大，便会出现过拟合现象，失去实际意义，所以k的选择一般小于等于3。图5a和图5b两图分别是对图4a中的两个选择区域的拟合效果图，图5c和图5d分别是对图4b中的两个选择区域的拟合效果图。其中点状为原始数据，带有方格的曲线代表单高斯拟合曲线，带有星号的曲线代表混合高斯拟合曲线，不带标志的曲线代表F-T分布拟合曲线。从拟合效果图（见图5）来看，F-T分布和混合高斯分布拟合效果接近，且明显优于单高斯分布。表6～表8中分别给出了对4个选择区域的曲线拟合效果的评价结果。从表6～表8中发现，F-T分布曲线与单高斯分布曲线相比，拟合效果要好很多，和混合高斯分布相比尽管差距不大，但是效果相对较好。实际应用中由于混合高斯分布形式过于复杂，因此并无太多应用价值。

Fig.4 OCT images of cardiovascular

Fig.5 Fitting results of Fig.4

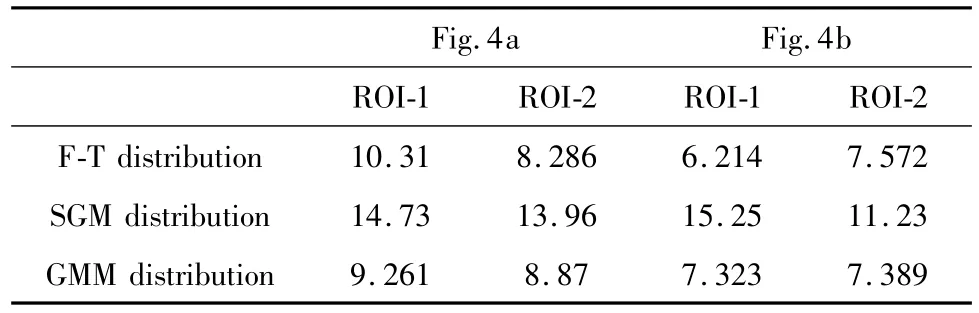
Table 6 RMSE testing results of Fig.4

Table 7 X2testing results of Fig.4

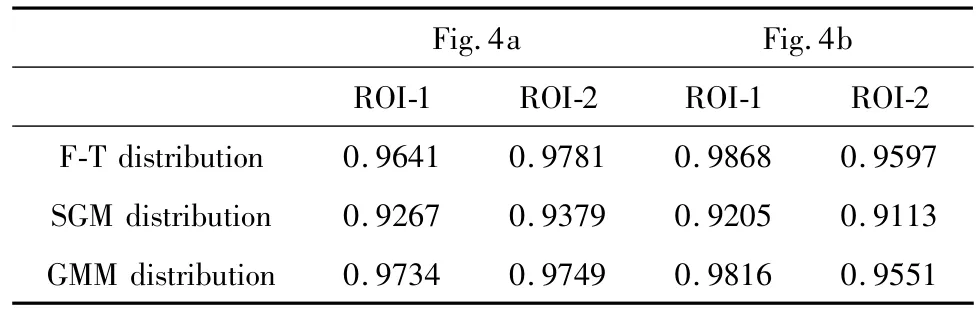
Table 8 R-square testing results of Fig.4

4 小 结

讨论了OCT图像的斑点噪声分布模型，并从理论上推导了斑点噪声对数变换之后的概率分布模型，最后通过实验进行了验证，证明对数域斑点噪声分布符合Fisher-Tippet分布。该模型将对OCT图像的去噪处理研究起到促进作用，例如在对图像进行去噪处理时，需要将图像的乘性噪声转化为加性，并得到变换后的图像的均值与方差，可以起到参考作用。作者主要集中分析OCT图像斑点噪声对数变换前后的统计特性，并没有进一步的分析变换后的Fisher-Tippet分布模型在OCT图像分析处理中的应用，因此接下来的工作需要细致分析Fisher-Tippett分布模型在OCT图像处理中的应用。

［1］ HUANG D，SWANSON E A，LIN C P，et al.Optical coherence tomography［J］.Science，1991，254（5035）：1178-1181.

［2］ FUJIMOTO JG，BOUMA B，TEAMEY G J，etal.New technology for high-speed and high-resolution optical coherence tomography［J］.New York Academy of Sciences，1998，838（l）：95-107.

［3］ QIN YW.Study on micro-electromechanical system measurement using optical coherencetomography［J］.Laser Technology，2013，37（5）：664-667（in Chinese）.

［4］ FERCHER A F，HITZENBERGER C K，KAMP G，et al.Measurement of intraocular distances by backscattering spectral interferometry［J］.Optics Communications，1995，117（5）：43-48.

［5］ SCHMITT JM，XIANG SH，YUNG K M.Speckle in optical coherence tomography：an overview［J］.Journal of Biomedicsl Optics，1999，4（1）：95-105.

［6］ GOSSAGE KW，SMITH C M，KANTER E M，et al.Texture analysis of speckle in optical coherence tomography images of tissue phantoms［J］.Physics in Medicine Biology，2006，51（6）：1563-1575.

［7］ GOODMAN JW.Statistical optics［M］.New York，USA：John Wiley＆Sons Inc，1985：122-125.

［8］ GOODMAN JW.Statistical properties of laser speckle patterns［M］.Heidelberg，Germany：Springer-Verlag，1980：1-50.

［9］ KARAMATA B，HASSLER K，LAUBSCHER M，et al.Speckle statistics in optical coherence tomography［J］.Journal of the Optical Society of America，2005，A22（4）：593-596.

［10］ XIEH，PIERCE L E，ULABY F T.Statistical properties of logarithmically transformed speckle［J］.IEEE Transactions on Geoscience and Remote Sensing，2002，40（3）：721-727.

［11］ SCHMITT JM.Optical coherence tomography（OCT）：a review［J］.IEEE Journal of Selected Topics in Quantum Electronics，1999，5（4）：1205-1215.

［12］ BOUMA B E，TEARNEY G J.Handbook of optical coherence tomography［M］.New York，USA：Marcel Dekker，2002：117-121.

［13］ ADLER D C，KO TH，FUJIMOTO JG.Speckle reduction in optical coherence tomography images by use of a spatially adaptive wavelet filter［J］.Optics Letters，2004，29（24）：2878-2880.

［14］ GUO Q，DONG F，SUN Sh F，et al.Image denoising algorithm based on contourlet transform for optical coherence tomography heart tube image［J］.Image Processing，2013，7（5）：442-450.

［15］ LEE P，GAOW R，ZHANG X L.Speckle properties of the logarithmically transformed signal in optical coherence tomography［J］.Journal of the Optical Society of America，2011，A28（4）：517-522.

［16］ WANG R，YUN JX，YUAN X C，et al.An approachfor megahertz OCT：streak mode Fourier domain optical coherence tomography［J］.Proceedings of the SPIE，2011，7889：788920.

Analysis of noise model of optical coherence tomography image in logarithm ic domain

JI Wen，SUN Shuifa，WANG Shuai，DONG Fangmin
（Institute of Intelligent Vision and Image Information，Three Gorges University，Yichang 443002，China）

In order to analyze the speckle noise distribution model of optical coherence tomography（OCT）images before and after logarithm transformation and provide references for image de-noising and other image processing，theoretical distribution model of the speckle noise was deduced firstly and then was verified by experimental results.First of all，the statistical properties of the speckle noise before the logarithm transformation were analyzed.The distribution model of the speckle noise after logarithm transform was derived through the mathematical theory.Then，the smooth regions of cardiovascular OCT images were selected as the experimental data to obtain the histogram distribution of the speckle noise before and after the logarithm transformation.Finally，the experimental data were fitted by the theoretical distribution model and the evaluated data，such as R-square，root mean square error and X-square tests.The results prove that the noise distribution after logarithm transformation presents Fisher-Tippett distribution.The results are helpful for the de-noising on OCT images.

image processing；noise model；logarithm transformation；optical coherence tomography image；speckle noise

TP391.4

A

10.7510／jgjs.issn.1001-3806.2014.06.027

1001-3806（2014）06-0848-06

国家自然科学基金资助项目（61272237；61272236）

纪 文（1989-），男，硕士研究生，现主要从事医学图像处理的研究。

*通讯联系人。E-mail：watersun＠ctgu.edu.cn

2013-12-06；

2014-01-02