一个腔中实现两种原子量子态的隐形传态
2014-06-23林初伦
林初伦
(温州大学物理与电子信息工程学院,浙江温州 325035)
一个腔中实现两种原子量子态的隐形传态
林初伦
(温州大学物理与电子信息工程学院,浙江温州 325035)
在一个外场驱动的腔QED系统中,利用三原子纠缠态作为量子信道,提出了任意单原子态和两原子纠缠态的隐形传态方案.该方案不受腔损和热场的影响.
腔QED;纠缠态;隐形传态
量子隐形传态在远程量子计算[1]、远程量子克隆[2]以及远程量子控制[3]等许多量子信息处理方案中都有重要的应用.自从1993年Bennett[4]等人首次提出隐形传态方案以来,人们又提出了很多关于实现量子态传送的理论和实验方案[5-13],如文献[7-10]利用腔QED系统实现了未知原子态的传送,文献[11]利用原子和腔的共振相互作用实现了未知原子态的传送,由于腔损和热场的影响,成功传送的概率是0.25.文献[12]利用GHZ态作为量子信道,在大失谐的情况下实现了原子纠缠态的传送,成功概率为0.5.文献[13]则通过增加一个经典驱动场,使得成功传送单原子态的概率达到了1.本文首先提出了利用三原子的最大纠缠态来实现一个由两个传送者配合来完成的隐形传态方案.由于两原子同时与一个单模腔和一个经典场发生作用,以至于腔损和热场的影响可以消除,成功的概率为1.然后,利用三原子的非最大纠缠态,又提出了一个以一定概率实现任意两原子纠缠态的传送方案.
1 系统的哈密顿量
两个相同二能级原子同时与经典场驱动的单模腔场发生相互作用,系统的哈密顿量[14]为(设ħ=1):
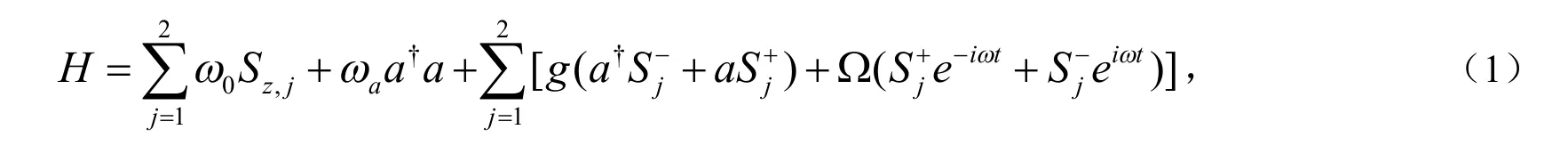
若ω=ω0,在相互作用表象中,系统的哈密顿量为:
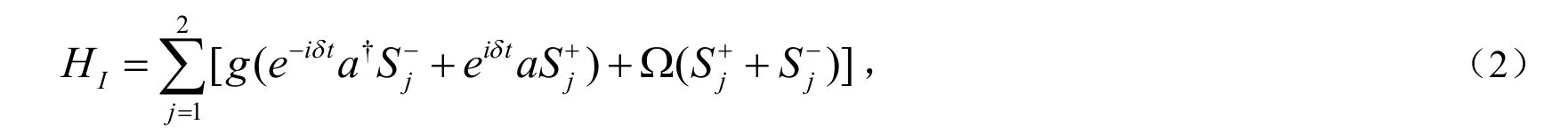
其中,δ为0ω和aω间的失谐量.对于强驱动场(Ω>>δ>>g),原子系统和腔场间没有能量交换,因此腔损和热场的影响可以忽略.利用旋波近似,系统的有效哈密顿量简化为[14]:

2 任意单原子态的隐形传态


表1 Alice的测量结果, 原子3、4的态, 原子4坍缩态以及Bob所做的幺正变换
3 两原子纠缠态的隐形传态

若要实现隐形传态,Bob需要制备另一个单模高品质共振光学腔(初态为真空态)以及一个光子探测器.

4 结 语
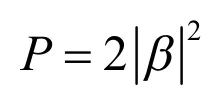
[1] Cirac J I, Ekert A, Huelga S F, et al. Distributed quantum computation over noisy channels [J]. Physical Review A, 1999, 59: 4249-4254.
[2] Murao M, Jonathan D, Plenio M B, et al. Quantum telecloning and multiparticle entanglement [J]. Physical Review A, 1999, 59: 156-161.
[3] Huelga S F, Vaccaro J A, Chefles A, et al. Quantum remote control: Teleportation of unitary operations [J]. Physical Review A, 2001, 63: 042303.
[4] Bennett C H, Brassard G, Grepeau C, et al. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels [J]. Physical Review Letter, 1993, 70: 1895-1899.
[5] 马刚龙, 查新未. 利用两个EPR态完全隐形传输四粒子W态[J]. 光子学报, 2010, 39(9): 1627-1630.
[6] 刘俊昌, 李渊华, 聂义友. 基于纠缠交换和团簇态实现两粒子任意态的可控隐形传态[J]. 光子学报, 2010, 39(11): 2078-2082.
[7] Cao Z L, Yang M. Probabilistic teleportation of unknown atomic state using W class states [J]. Physica A, 2004, 337:132-140.
[8] Zheng S B, Guo G C. Teleportation of atomic states within cavities in thermal states [J]. Physical Review A, 2001, 63: 044302.
[9] Cao Z L, Yang M, Guo G C. The scheme for realizing probabilistic teleportation of atomic states and purifying the quantum channel on cavity QED [J]. Physical Letter A, 2003, 308: 349-354.
[10] Li W L, Li C F, Guo G C. Probabilistic teleportation and entanglement matching [J]. Physical Review A, 2000, 61: 034301.
[11] Zheng S B. Scheme for approximate conditional teleportation of an unknown atomic state without the Bell-state measurement [J]. Physical Review A, 2004, 69: 064302.
[12] Ye L, Guo G C. Scheme for teleportation of an unknown atomic state without the Bell-state measurement [J]. Physical Review A, 2004, 70: 054303.
[13] Yang M, Cao Z L. Scheme for deterministic Bell-state-measurement-free quantum teleportation [J]. Int J Quant Inform, 2006, 4(2): 341-346.
[14] Zheng S B. Generation of entangled states for many multilevel atoms in a thermal cavity and ions in thermal motion [J]. Physical Review A, 2003, 68: 035801.
[15] Xue Z Y, Yang M. Teleportation for atomic entangled state by entanglement swapping with separate measurements in cavity QED [J]. Optics Communications, 2006, 258: 315-320.
Teleportation of Two Atomic States in a Thermal Cavity
LIN Chulun
(School of Physics and Electronic Information Engineering, WenZhou University, WenZhou, China 325035)
A scheme is presented to teleport an arbitrary single atomic state and an unknown entangled quantum state of two atoms using an entangled quantum state of three atoms in driven cavity QED. In addition, the scheme is insensitive to the cavity and the thermal field.
Cavity Quantum Electrodynamics; Entangled State; Teleportation
O431
A
1674-3563(2014)02-0022-05
10.3875/j.issn.1674-3563.2014.02.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:王一芳)
2013-11-11
林初伦(1991- ),男,浙江温州人,硕士研究生,研究方向:量子信息物理
