基于数据融合算法优化的GM(1,1)模型在矿区地表沉降中的应用

杨 军，马大喜

(江西理工大学研究生院，江西赣州 341000)

基于数据融合算法优化的GM(1,1)模型在矿区地表沉降中的应用

杨 军，马大喜

(江西理工大学研究生院，江西赣州 341000)

矿区地表沉降一直以来是矿山安全管理部门关注的重点，准确地预测矿区地表沉降可以给矿山安全带来指导性的意义．运用“幂函数-指数函数”的复合变换来提高监测原始数据的平滑度，然后对具有多个沉降监测数据的特定年份，运用GM(1,1)模型来预测地表沉降，利用数据融合算法对多次预测的结果进行优化分析，获得精度较高的预测结果．运用该方法对某矿区地表沉降数据进行预测，结果表明该模型具有良好的预测能力．

数据融合；复合变换；GM(1,1)模型；沉降预测

矿区地表沉降引起的局部坍塌和相邻地区的不均匀沉降给矿区带来了安全隐患，因此对矿区的地表沉降预测就显得尤为重要．目前，对矿区地表沉降预测方法研究很多，如负荷密度法、回归分析法、灰色预测法、神经网络法等[1]．GM(1,1)模型是一种对“小样本”、“贫信息”进行分析的灰色预测法[2]．原始数据列的平滑度直接关系到该模型的预测精度，数据的突变和奇异也会导致预测精度降低．针对以上实际问题，本文采用“幂函数-指数函数”复合变换对原始数据进行处理，使得数据更加平滑，然后运用GM(1,1)模型对不同样本数的历史监测数据进行预测，将得到的多个预测数据进行数据融合优化，避免了因个别数据的突变性偏差导致预测结果误差较大．通过实例验证，该模型方法切实可行，具有较高的预测精度．

1 幂函数-指数函数复合变换原理

国内对提高原始数据列平滑度方面已经有一定的研究，如学者李群提出[3]利用对数函数及开方变换、王建根和李春生提出[4]用对数函数开方的复合变换等数据平滑方法．不同的方法都在传统的基础上有所改进和提高，本文采用“幂函数-指数函数”复合变换a-xm(a＞1,m＞1)来处理原始数据列，将x(0)(k)变换成a[x(0)(k)]m，对变换后的原始数据{a[x(0)(k)]m}进行预测，把预测结果再还原，使其效果更加明显，数据列平滑度有显著提高．

该复合变换的基本原理如下：

若x(k)为递增数列，且x≥e,a＞1,m≥1,T≥1，并且m＞T，则：

2 GM(1,1)模型

灰色理论模型是对贫信息，信息不完全的数据进行建模分析，对事物发展规律作出模糊性长期描述，其中GM(1,1)模型运用最为广泛．GM(1,1)模型表示1阶的、1个变量的微分方程模型[5]，设预测对象为非负单调的原始负荷数据列x(0)={x(0)(1),x(0)(2),…,x(0)(n)}，其通过一次累加生成序列x(1)：

3 数据融合优化下的GM(1,1)模型

3.1 数据融合算法基本原理

3.2 优化模型建立的过程

GM(1,1)是一种针对小样本、贫信息的数据序列进行模拟预测的模型，其不需要考虑数据的分布规律和变化趋势等[7]．在实际运用过程中，人们往往希望能够提高预测的精度和准确性，并且避免预测上的错误，但在采集数据的过程中，会因为人为因素或者仪器、环境等主客观原因导致数据出现偶然性偏差，如若直接采用该模型会导致预测精度随偏差的增大而大大降低；另一方面，GM(1,1)模型的预测精度与原始数据的平滑度息息相关．为提高原始数据的平滑度，避免因原始数据突变性偏差而导致预测结果误差偏大的问题，本文利用“幂函数-指数函数”的复合变换来提高原始数据的平滑度，利用不同样本数的历史数据建立GM(1,1)模型来预测分析，将不同的预测值用数据融合的方法进行综合分析，得到最终优化结果．

优化模型流程如图1所示，首先将原始数据进行“幂函数-指数函数”变换，然后分别选取预测年数j年之前4、5、6、……、j-1作为建模数据预测j年的值，然后各个预测值还原，用数据融合优化得出最优结果．

图1 基于数据融合算法优化的GM(1,1)模型算法流程图

4 实例分析

运用普通的GM(1,1)模型和本文提出的基于数据融合算法优化的GM(1,1)模型对某矿区2007年地表移动观测站某点的实测资料进行沉降预测，验证本文的方法具有精度高的优势．该矿山对沉降点每周观测一次，采用该观测数据中的8期数据进行分析，在建模预测的时候采取该数据的前4期数据作为建模数据，后4期数据作为预测数据进行比较分析．

图2是该矿山的监测点分布图．

表1是普通GM(1,1)模型和数据融合算法优化GM(1,1)模型的模拟预测结果比较，从表1可以看出经过数据融合优化GM(1,1)的模型预测精度明显高于普通的GM(1,1)模型预测精度，预测值的最小相对误差达到了5.43%，平均相对误差也明显占优，预测精度更高．

图3是原始数据经过“幂函数-指数函数”处理前后的数据曲线对比，原始数据通过运用MATLAB编写“幂函数-指数函数”变换程序实现．从图3可以看出经过“幂函数-指数函数”复合变换后的原始数据更加平滑，在预测中可以有效提高GM(1,1)模型预测精度．

图2 某矿山沉降监测点分布图

图4是原始数据、普通GM(1,1)、优化GM(1,1)三种数据的曲线对比图，普通GM(1,1)、优化GM(1,1)均通过MATLAB进行实现．从图4可以看出优化处理后的GM(1,1)数据比普通GM(1,1)更加接近于原始数据．

图5是沉降数据经过GM(1,1)模型优化前后预测效果的相对误差对比图．从图5可以看出，优化的GM(1,1)曲线更加接近于零，即其相对误差更小，更加接近于真实值．

通过实例分析表明，基于数据融合优化的GM(1,1)模型在矿区地表沉降的预测中，精度较好，可靠性较高，具有实用价值．

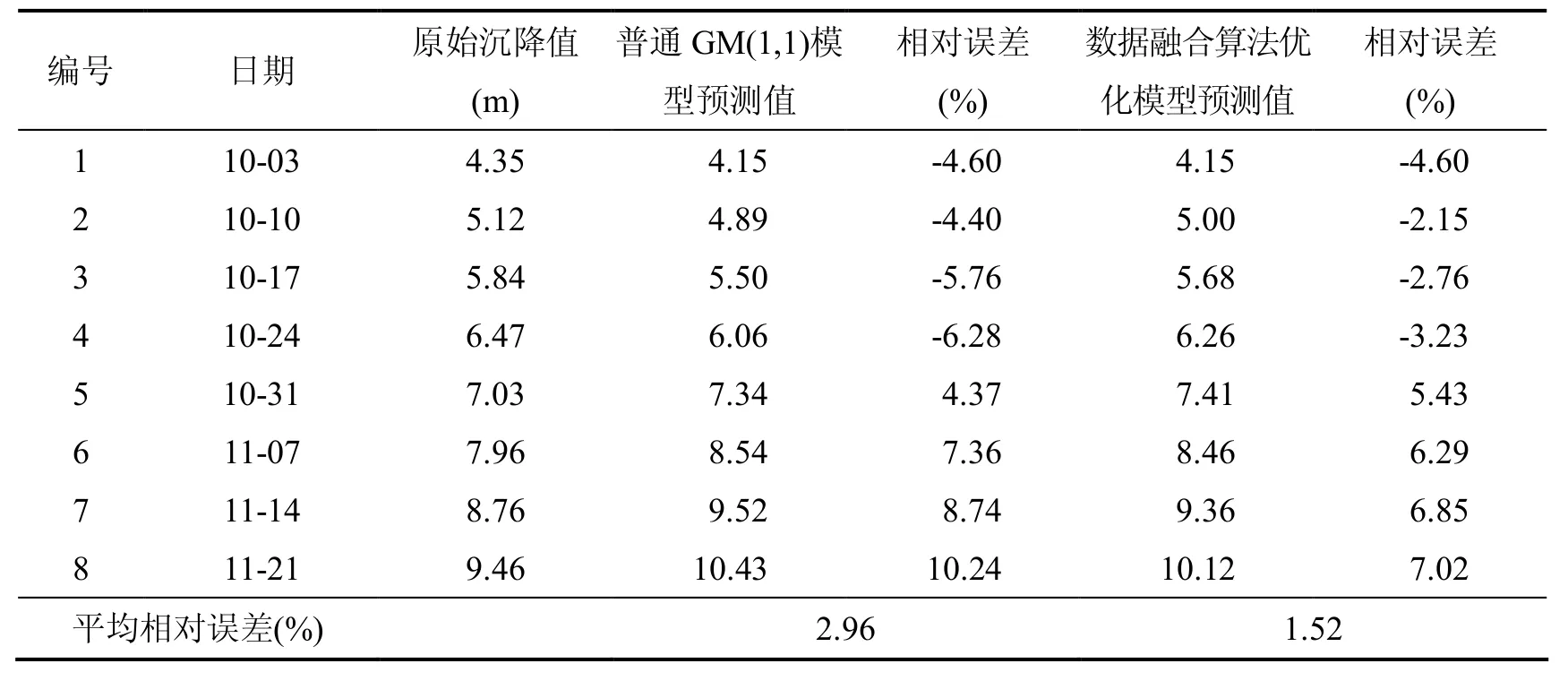
表1 普通GM(1,1)模型和数据融合算法优化模型的模拟预测结果比较

图3 原始数据变换前后曲线对比

图4 GM(1,1)模型优化前后预测效果对比

5 结 论

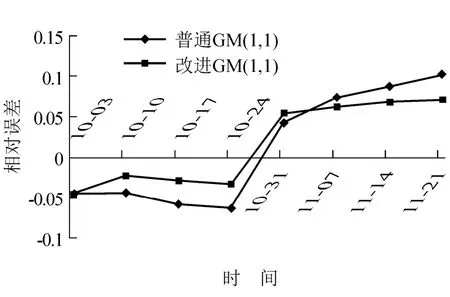
图5 GM(1,1)模型优化前后预测相对误差对比

（1）“幂函数-指数函数”复合变换是一种有效的提高数据列平滑度的的方法，可以提高GM(1,1)模型预测的精度．

（2）基于数据融合优化的GM(1,1)模型较之普通的GM(1,1)模型，采用不同样本数的原始数据进行模拟预测和对多结果进行优化，有效避免了因个别原始数据的突变和奇异所导致预测结果有较大的偏差，最大限度地对原始数据进行挖掘，提高了预测结果的可靠性．

（3）该模型方法在中长期预测中精度较好，可作为矿区长期地表沉降预测的实用方法．

[1] 肖海平, 陈兰兰. 灰色理论模型在矿山变形监测中的应用[J]. 金属矿山, 2009(1): 154-155.

[2] 邓聚龙. 灰色控制系统[M]. 武汉: 华中工学院出版社, 1985: 175-177.

[3] 李群. 灰色预测模型的进一步拓广[J]. 系统工程理论与实践, 1993, 13(1): 64-66.

[4] 王建根, 李春生. 灰色预测模型问题的一个注记[J]. 系统工程, 1996, 14(6): 14-15.

[5] 邓聚龙. 灰色系统的模型[J]. 模糊数学, 1985, 4(2): 5-8.

[6] 孟欣, 李郁侠. 基于数据融合算法优化的GM(1,1)负荷预测模型[J]. 西安理工大学学报, 2012, 28(4): 499-452.

[7] 肖俊, 孙德宝, 秦元庆. 灰色模型在电力负荷预测中的优化与应用[J]. 自动化技术与应用, 2005, 24(2): 19-21.

Application of GM (1.1) Model in Mining Surface Subsidence Based on Optimization Algorithm of Data Fusion

YANG Jun，MA Daxi
(Graduate School, Jiangxi University of Science and Technology, Ganzhou, China 341000)

Surface subsidence in mining areas is always the focus concerned by the safety department of mines. Thus, accurate prediction of surface subsidence in mines means significantly to mine safety. We can make use of the composite conversion of "power function-exponential function" to improve the evenness of monitoring primary data and then to predict the ground surface settlement by means of GM(1.1) Model regarding to a particular year with multiple settlement monitoring data. The optimized analysis to results of multiple predictions is made out of data fusion in order to obtain more accurate prediction results. The author ever made a mining area subsidence prediction in this method, which turn to prove that GM(1.1) Model possesses an ideal predictive power.

Data Fusion; Composite Conversion; GM (1.1) Model; Subsidence Prediction

TD173

A

1674-3563(2014)02-0051-07

10.3875/j.issn.1674-3563.2014.02.008 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：封毅)

2013-11-25

杨军(1989- )，男，重庆，硕士研究生，研究方向：大地测量学，测量数据处理和统计分析