三维真比例导引弹道仿真分析
2014-06-23郝士林
郝士林 严 超 雷 璐 毕 进
(西安电子工程研究所 西安 710100)
0 引言
比例导引法是在自寻的导弹上采用较多的一种导引规律,它是指导弹飞向目标的过程中,导弹速度方向的变化率与目标视线的成正比例。这种导引律有利于工程实现,同时选择适合的导引比,就不会需要太大的法向过载,对不同机动特性的目标适应能力也较强[1]。而真比例导引律产生垂直于弹目视线的指令加速度,它与弹目视线距离变化率和弹目视线角速度变化率成正比,在命中点处的需用过载不仅与导弹速度无关,而且与导弹攻击的方向也无关,相对于经典的比例导弹方法来说更具有优势,有利于全向攻击[2]。
1 三维真比例导引弹道仿真
1.1 弹目运动模型建立
在大地坐标系下分析拦截模型的运动参数,图1表示某时刻弹目相对运动关系,T表示目标,M表示导弹,θt为目标速度倾角,θm为导弹弹道倾角,φt为目标速度偏角,φm为导弹弹道偏角。求解相关变量:
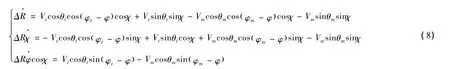
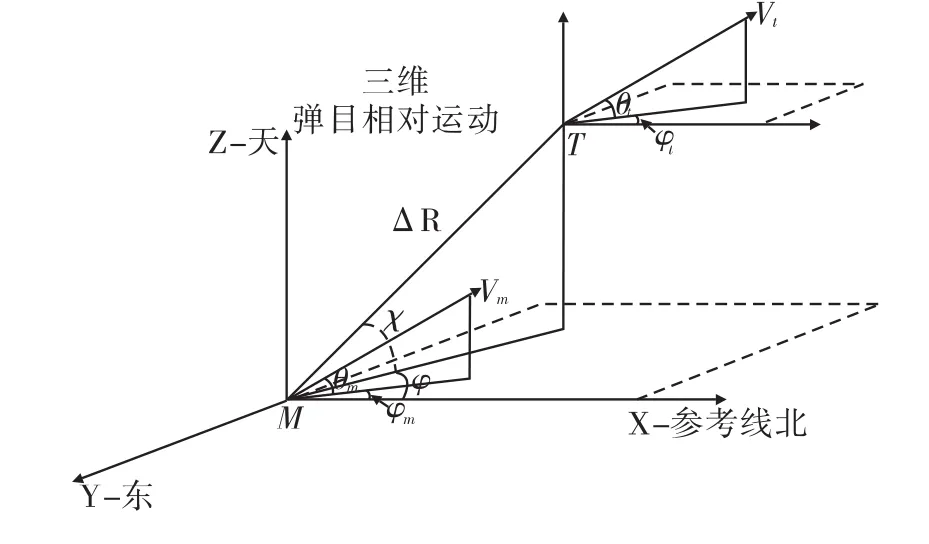
图1 三维弹目相对运动示意图
1.2 指令加速度方程
相关文献[3-6]已经指出真比例导引律的指令加速度am施加于垂直于弹目视线的方向,其大小正比于弹目接近速度和视线角速率的乘积:

为了便于方程的计算,将导弹运动分解到垂直平面和水平面运动。即将产生的指令加速度分解为俯仰指令加速度和偏航指令加速度,其加速度方程:

1.3 仿真实现
A.仿真环境:vc++6.0,matlab 2010
B.仿真步长:10ms
C.目标运动参数:
目标初始为匀速直线运动,初始条件为a,当弹目距离为60km时,目标开始正弦机动机动条件满足b,比例导引系数:k=3。
a.匀速情况

b.垂直平面正弦机动情况
T=20s,A=500m
D.
在VC下,通过4阶龙格库塔算法,对弹道方程求解后,存计算结果到本地文件。用matlab读取仿真数据绘图。仿真结果图如下,图2为弹目飞行曲线,OP和PM分别表示目标做匀速直线飞行和正弦机动飞行,与此对应的导引弹道为AB和BM。图3、图4、图5为导弹的需用过载曲线,点B表示此时目标开始机动。
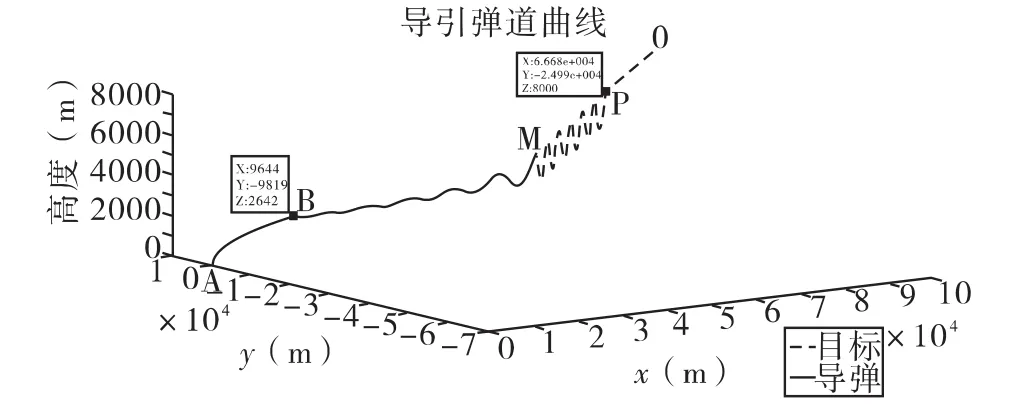
图2 导引弹道图
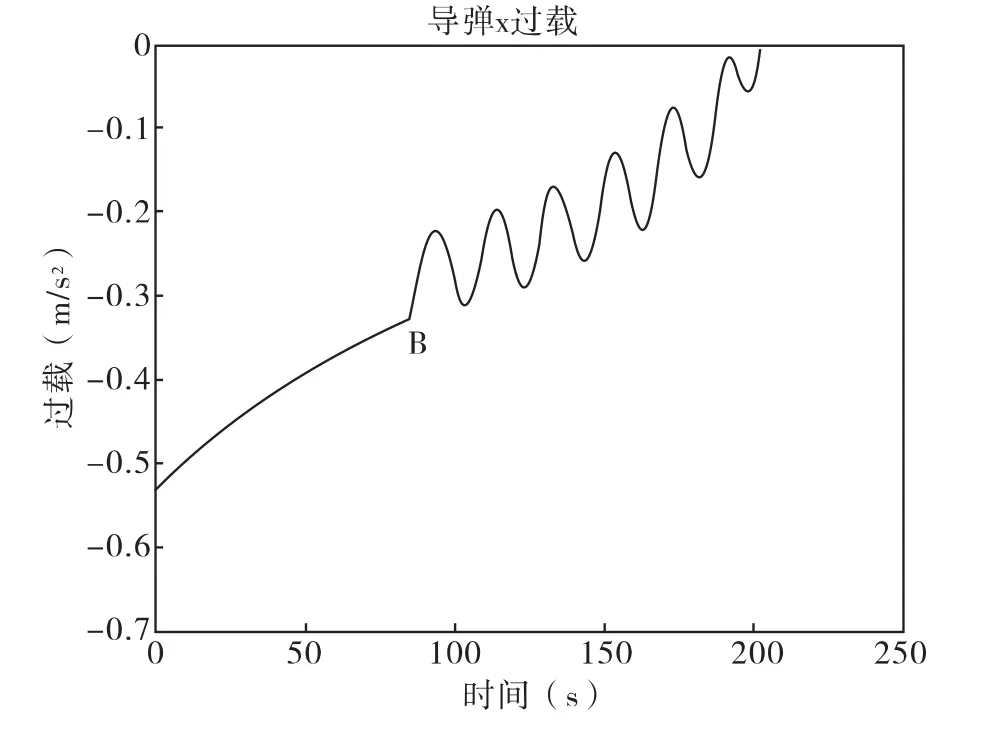
图3 导弹x轴过载
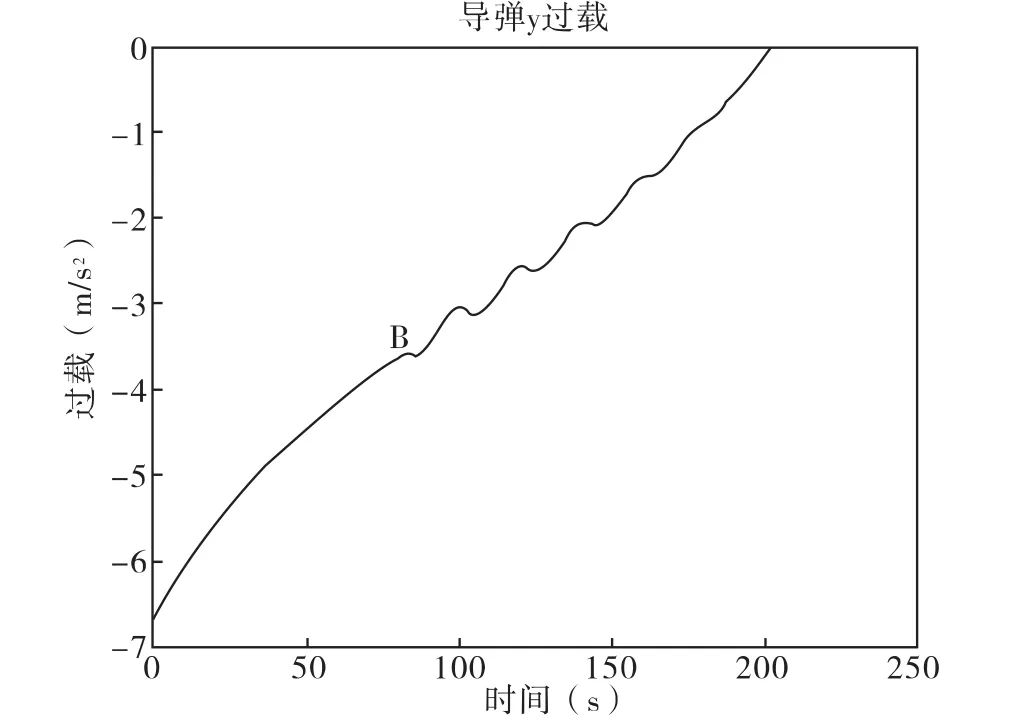
图4 导弹y轴过载
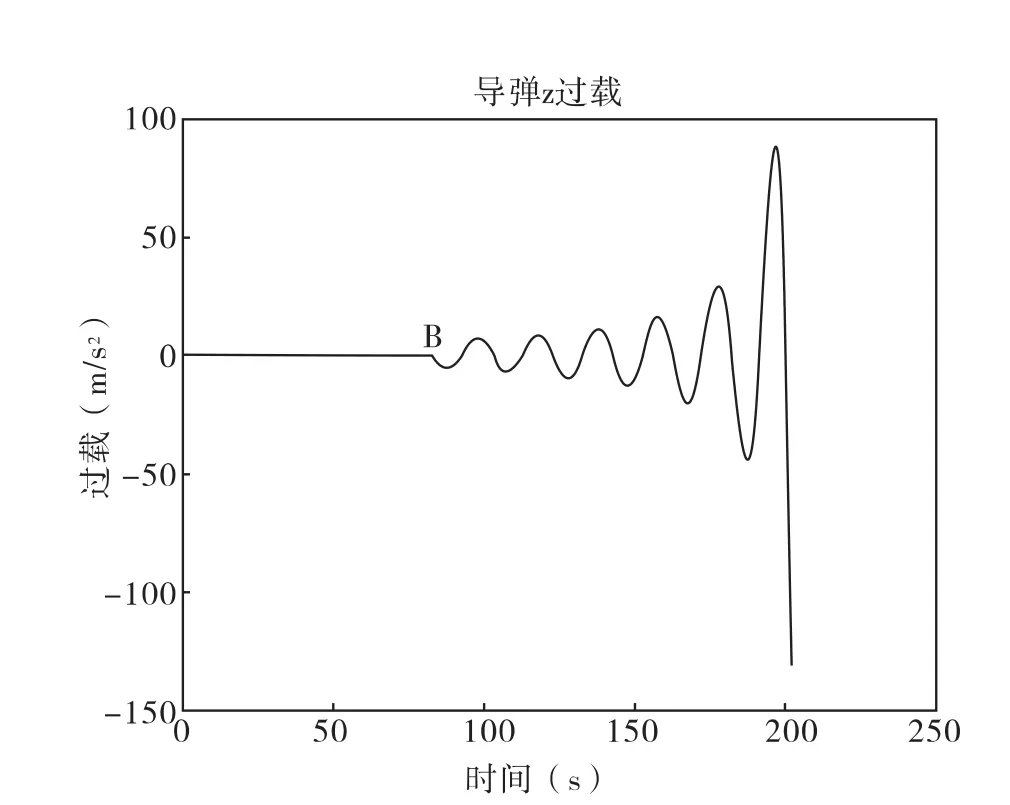
图5 导弹z轴过载
1.4 仿真结果分析
图1中,初始段OP目标匀速直线飞行,弹目相对距离较远,弹目视线角速度变化均匀,致使需用指令加速度变化均匀,所以导引弹道AB段较平直。目标机动段PM,弹目视线角速度变化较大,所需加速度指令也发生较大变化,导引弹道BM相对弯曲;目标机动在弹目相对距离较远时引起的视线角速度变化率比弹目距离较近时引起的视线角度变化率小,所以导引弹道BM段,前段比后段要缓一些。理论分析的指令加速度变化趋势与实际仿真图2、图3和图4是相符的。但在图4中可以看出由于目标机动的原因,在末端导弹的需用过载很大,甚至很难实现,所以在对付大机动目标时制导精度较差。仿真结果与理论分析相符,验证了将三维导引弹道分解计算的可行性。
2 结束语
本文基于飞行器真比例导引原理,建立弹目相对运动的导引方程,以龙格库塔法为工具,以弹道投影分解计算为方法[7-9],在VC环境下,对三维真比例导引弹道进行仿真。仿真结果与理论分析相符,表明了对三维导引弹道分解计算的可行性。友好的仿真环境以及通用的求解算法使程序具有较强的可移植性,而仿真中一些没有考虑的诸因素,需要进一步分析研究。
[1]孙中南、童幼堂、张卫峰.比例导引法导引弹道仿真研究[J].战术导弹技术,2005,(2):56-59.
[2]钱杏芳、林瑞雄、赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2011.
[3]卫星、王艳东.真比例导引律的解析解研究[J].火力与指挥控制,2009,34(8):84-86.
[4]欧阳中辉、刘家祺、张龙杰、叶文.基于矢量运算的三维真比例导引弹道仿真[J].弹箭与制导学报.2013,33(1):53-56.
[5] 毕开波、王晓东、刘智平.飞行器制导与控制及其Matlab仿真技术[M].北京:国防工业出版社,2009.
[6] 李军林、袁湛.三维修正比例导引弹道仿真研究[J].机械管理开发,2009,(2):161-162.
[7]张建伟、黄树彩、韩朝超.基于Matlab的比例导引弹道仿真分析[J].战术导弹技术,2009,(3):60-64.
[8]欧阳瑜、李刚、高忠长.基于Matlab的防空导弹三维弹道仿真[J].火力与指挥控制,2010,35(2):166-168.
[9]赵蕴杰、曹迎春、张青斌.基于Matlab的三维动态弹道仿真研究[J].计算机仿真,2007,24(6):57-61.
