DBS成像技术在毫米波雷达导引头中的应用

张 辉 黄 默 曲春辉

(中国科学院电子学研究所 北京 100190)

0 引言

20世纪70年代以来，世界各军事大国掀起了以军事应用为先导的毫米波研究，各种不同类型的毫米波精确制导武器不断研制成功并相继装备部队使用。毫米波雷达具有较窄的波束宽度，天线增益高，同时又有较大的带宽，因此可以实现距离向高分辨率;工作波长短，对多普勒频移敏感。毫米波雷达综合了微波、红外和可见光传感器的优点，具有独特的电波传播特性和广阔的军事应用前景［1］。总的来看，基于高精度距离分辨的一维成像技术已经相对成熟，国外正在走向基于宽带和横向相参滤波的二维成像技术研究。本文简述了一种常见的高分辨率雷达成像技术——DBS在毫米波雷达导引头中的应用。

1 DBS基本概念及工作原理

1.1 DBS基本概念

多普勒波束锐化(DBS)技术是目前广泛应用的高分辨率雷达成像技术之一，它具有运算负荷低、成像面积大的优势，因此在战场侦察等领域有着广泛的应用。利用DBS技术可以对目标区域的实时成像，结合相应的检测技术可以实现对目标的精确打击。1951年美国科学家Wiley首先提出了DBS原理，此后几十年间国外在此领域的理论和应用中发展很快。美国海军的S-3、空军的F-16等多种现役战机、预警机、无人机均装配了具有DBS功能的雷达系统［2］。

DBS与单脉冲雷达相比，无论是静目标还是动目标的检测能力都远远高于后者。因为单脉冲方位向的分辨率对应实孔径雷达的束宽，这将导致极低信杂噪比和检测性能。图1是两者在相同参数(距离分辨率1.14m)下的信杂噪比对比。

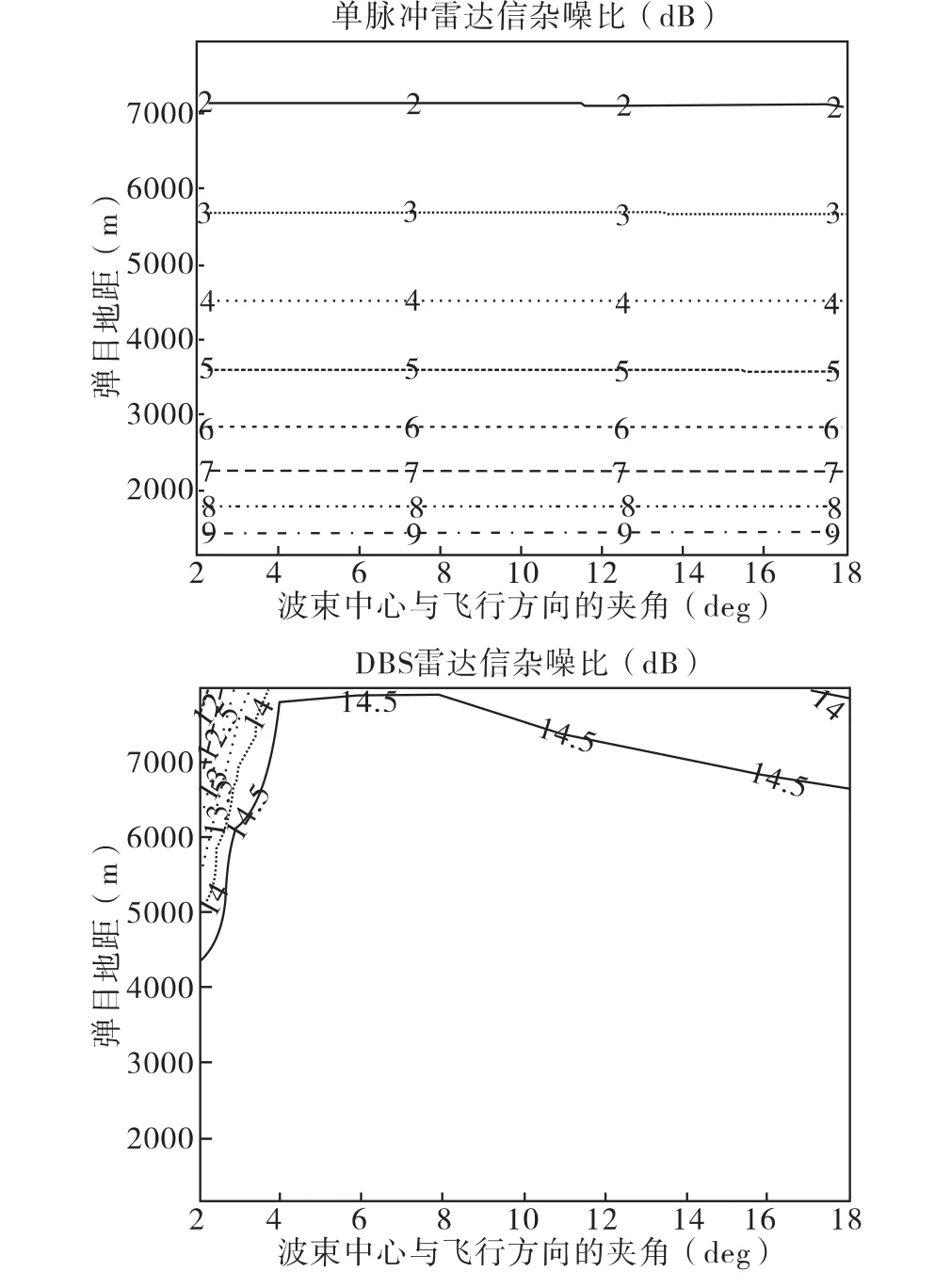
图1 单脉冲雷达与DBS雷达信杂噪比对比

1.2 DBS工作原理

DBS技术是用频谱理论来提高雷达方位向分辨率，即角分辨率。其本质是利用合成孔径技术进行快速成像，属于非聚焦SAR［3］。DBS技术将实孔径天线波束分割成若干较窄的子波束，利用雷达回波信号合成较大的天线孔径，因此实际波束由许多子波束组成。而且各子波束中心目标相对雷达的径向运动速度不同，因而各子波束回波多普勒频差不同。对中频雷达回波信号进行数字下变频得到基带信号后经过快速傅里叶变换(FFT)得到各子波束目标的多普勒频率差异。如果不同子波束目标的多普勒频移大于多普勒频率分辨率时，通过一组与子波束中心和带宽相对应的窄带滤波器，我们便可实现多普勒频率的分割，区分出位于不同子波束的目标，实现不同目标的方位向分辨，即角度分辨。系统的多普勒分辨率，即窄带滤波器组的分辨率取决于DBS的脉冲积累时间。多普勒波束锐化的示意图如图2所示。Δβ为实孔径天线波束投影，δβ为经过多普勒波束锐化的子波束宽度。

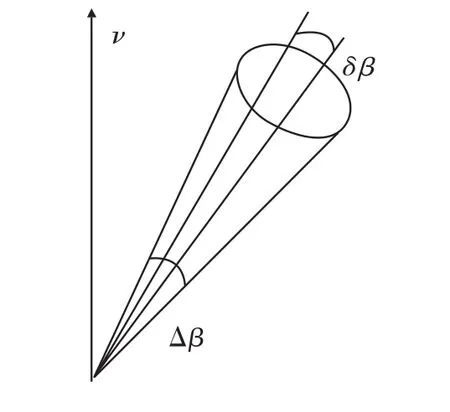
图2 DBS波束锐化示意图

如图3所示，设载机以速度va沿x方向匀速飞行，天线主波束照射区域内点目标A距离雷达R0，θ为方位角，φ为俯仰角，波束宽度为Δθ。设脉冲发射重复率为PRF，相干积累点数为Ka，相干处理时间为TDBS，则锐化比为:

由(1)式可以得到，多普勒锐化比反比于雷达系统的脉冲重复频率PRF，而正比于系统方位向的采样点数N。当PRF与N固定时，雷达天线的扫描角度越小，多普勒锐化比越大。

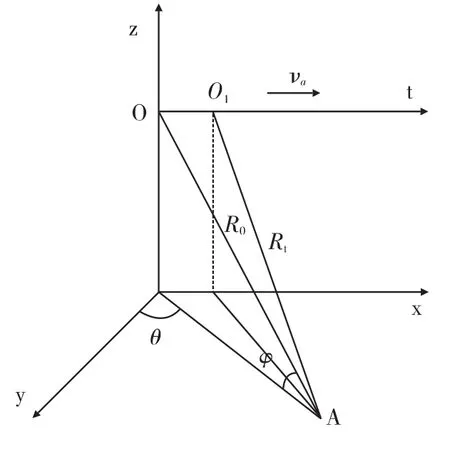
图3 DBS目标成像信号模型

2 DBS成像算法

实现DBS雷达导引头的关键在于DBS成像算法。为了得到具有较好信噪比的雷达回波信号以便于后续目标的恒虚警检测，毫米波DBS雷达导引头对系统的实时性具有较高的要求，当务之急是找到一种适合快速实时成像的算法。另一方面，为了得到在距离向和方位向都具有较高分辨率的目标图像，我们要求应用于DBS雷达导引头的成像算法具有良好的聚焦性能。因此，结合毫米波雷达回波信号的特点，我们找到了一种适合快速实时成像、聚焦效果好且在工程上较易实现的成像算法——SPECAN 算法。

2.1 SPECAN算法简介

在毫米波雷达导引头中，对方位向的分辨率与合成孔径雷达相比要求并不高，同时弹上导引头信号处理器的运算能力和存储能力也有较大的限制。因此，在这种情况下对雷达回波信号运用SPECAN成像算法处理，不需要繁杂的运算就能够快速得到信噪比较好的目标区域DBS图像。在距离向上，SPECAN算法对回波信号进行经典的脉冲压缩处理，利用匹配滤波的原理得到一维距离向图像，再在方位向上进行距离走动校正和FFT处理得到距离多普勒域的二维DBS图像。由于该算法是通过目标的多普勒中心频率确定其相对位置或者速度，该算法又被称为频谱分析算法。

2.2 回波信号模型

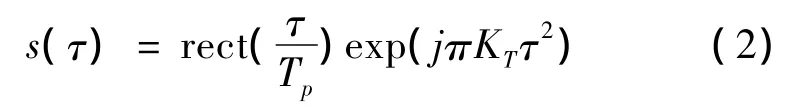
为了实现距离向的高分辨率，毫米波DBS雷达通常发射的是具有较大带宽的线性调频信号，设调频率为KT，宽度为TP，其表达式为:t时刻O1导引头与目标的瞬时斜距为Rτ，t是慢时间，τ是快时间。设合成天线孔径长度为L，合成孔径时间 TB，则是合成孔径天线的波束中心对应时间。天线衰减系数和方向图通常忽略，由此得到雷达回波信号的表达式:

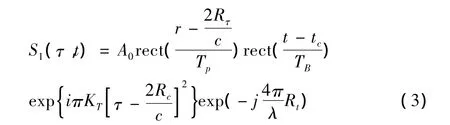
式中，A0为任意复常量。

2.3 距离向脉冲压缩

在距离向上，SPECAN算法采用了雷达领域经典的脉冲压缩算法，较大的调频带宽保证了距离向的高分辨率。根据匹配滤波理论，匹配滤波器的时域表达式如下:

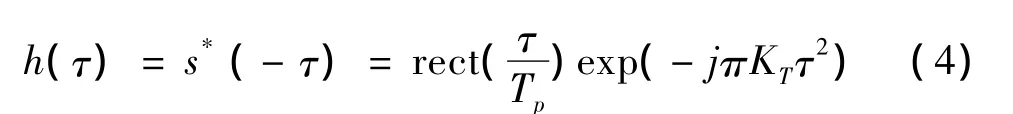
将匹配函数与雷达回波信号在频域相乘再做逆傅里叶变换(IFFT)得到经过脉冲压缩处理后的回波信号时域表达式:

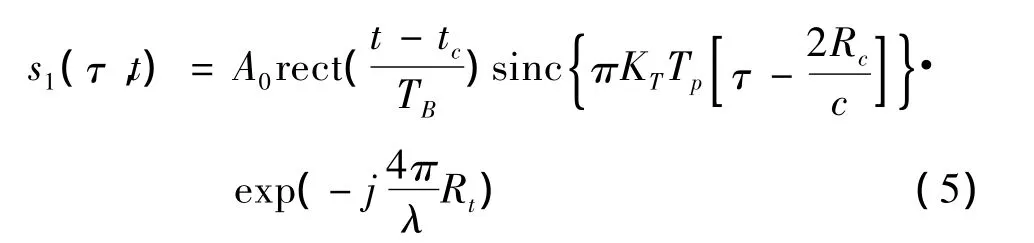
2.4 距离徙动校正

毫米波DBS雷达成像时，回波信号包络时延主要受到距离徙动的一次项，即距离走动的影响，而距离徙动其他高次项可以忽略［4］。因此，为了去除距离走动对信号的影响，我们需要将脉冲压缩处理后的一维信号在频域乘以距离走动补偿因子ω(f)。

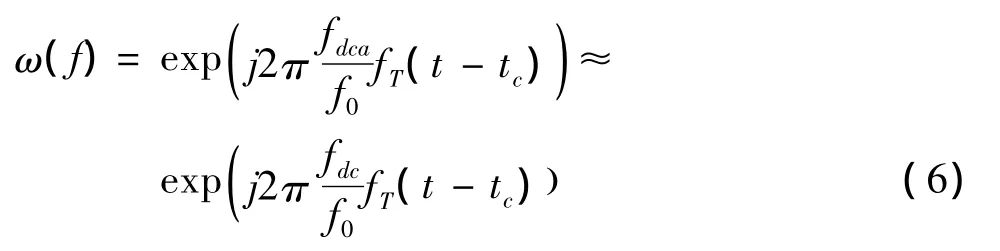
其中f0是系统载频;fT是距离频率。多普勒中心频率在实际工程应用时，我们通常用一维脉压信号估算出多普勒中心频率fdc以代替fdca。经过距离走动校正后，再进行IFFT得到信号表达式为:

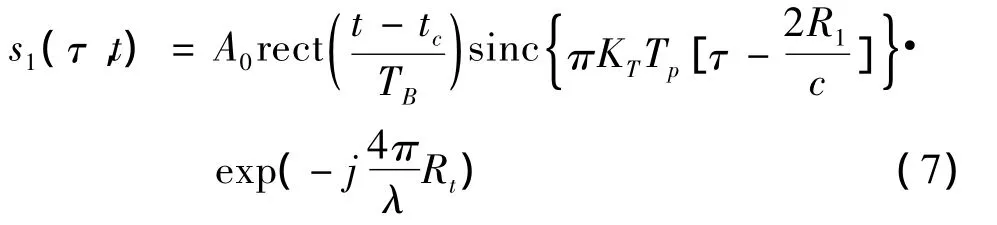
其中R1是合成孔径中心到目标的斜距。然后在方位向进行FFT即可得到DBS图像用于后续的恒虚警检测、跟踪、测角等。

2.5 SPECAN算法处理流程图

通过上述分析，毫米波DBS雷达成像处理的流程图如图 4 所示［5］。

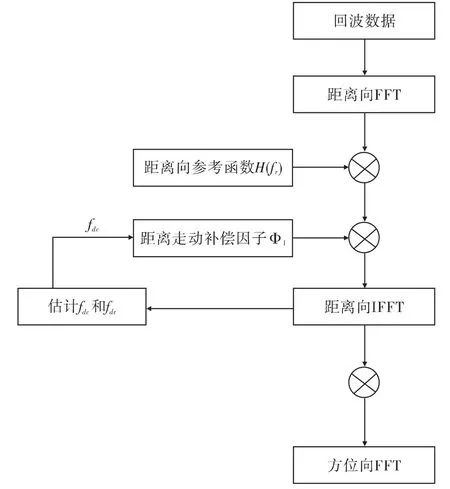
图4 毫米波DBS雷达成像处理的流程图

DBS输出的图像为距离多普勒域图像，可分成杂波(含静目标)图像和动目标图像两部分，两者在多普勒域图像中出现的位置不同。杂波的多普勒频率由导弹速度及天线方位向扫描角度决定，其宽度由天线方位向波束宽度决定。而动目标的多普勒频率除由上述两个参数决定外，还取决于目标的运动速度，当动目标的速度满足一定条件时，即目标回波多普勒频率大于系统的多普勒分辨率时，其多普勒频谱将偏出杂波谱，此时只需与较低的噪声功率相抗衡即可完成检测。

3 仿真结果

下面给出一种静目标跟踪模式下的系统仿真结果。该工作模式的系统参数见表1。

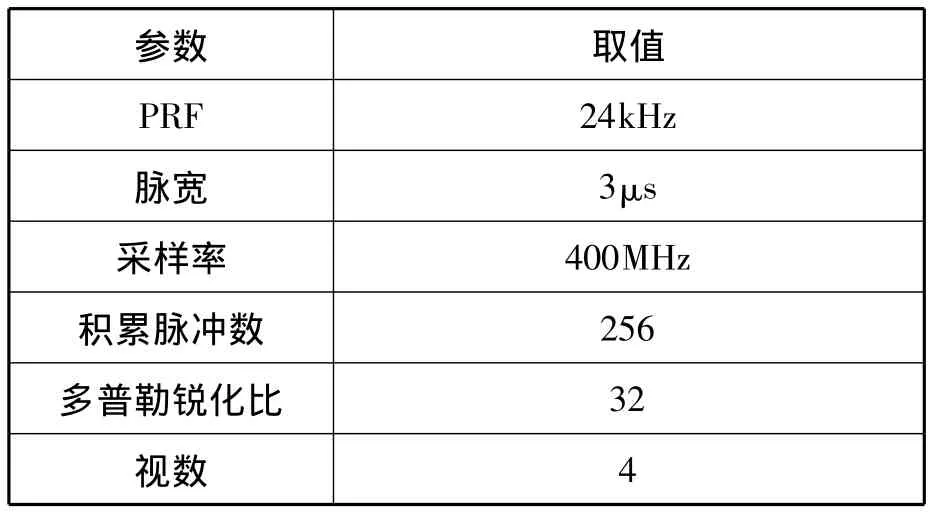
表1 静目标跟踪模式仿真参数

仿真结果和性能参数如图5、6、7、8和表2所示。

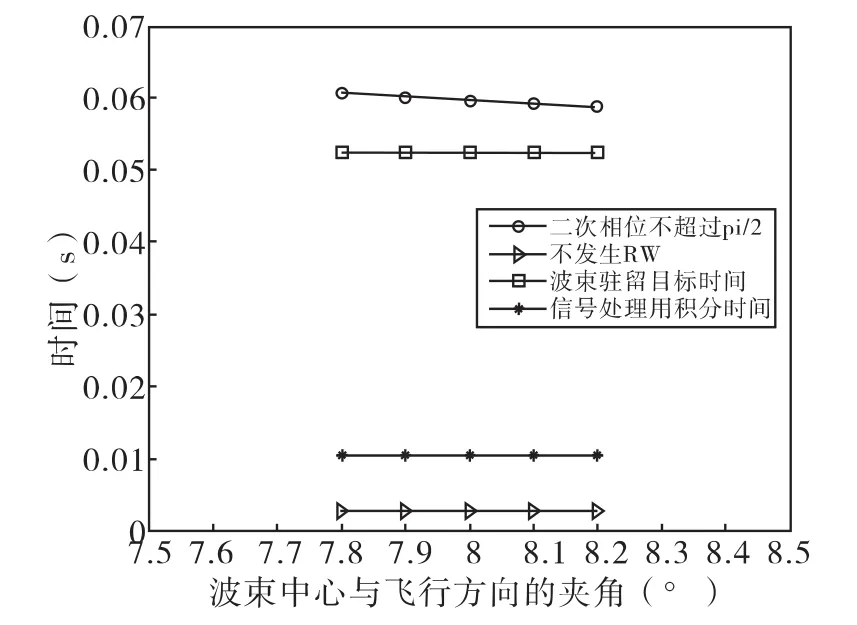
图5 毫米波DBS雷达静目标仿真结果1

由图4可以看出，脉冲积累的时间满足二次相位和距离走动量的限制。图5则展示了不同的多普勒带宽对应的方向向分辨率，由此看出采用DBS技术的毫米波雷达可以获得较高的角度分辨率和方位分辨率，同时可以区分动目标和静目标。图6和图7则是点目标和拓展目标的信噪比仿真。对于点目标和扩展目标的最差信杂噪比(14.99dB)，我们也可以实现恒虚警检测。

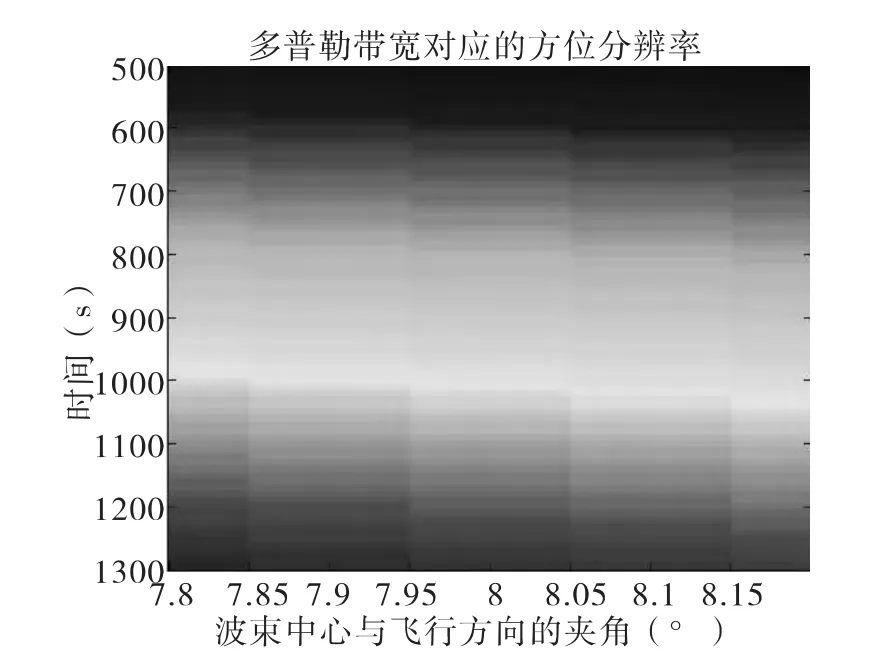
图6 毫米波DBS雷达静目标仿真结果2

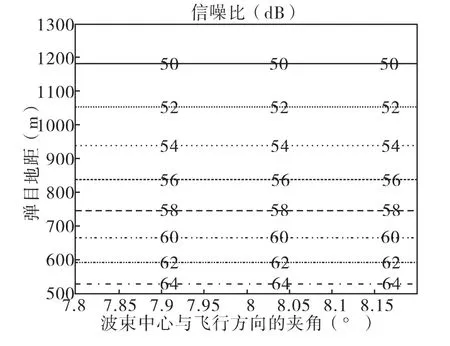
图7 毫米波DBS雷达静目标仿真结果3

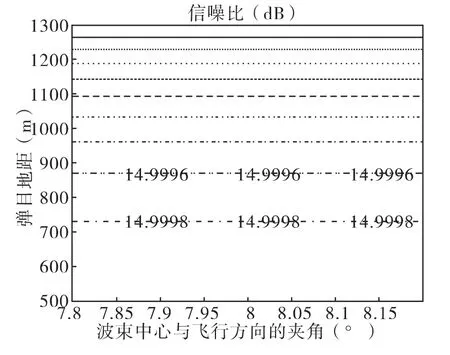
图8 毫米波DBS雷达静目标仿真结果4

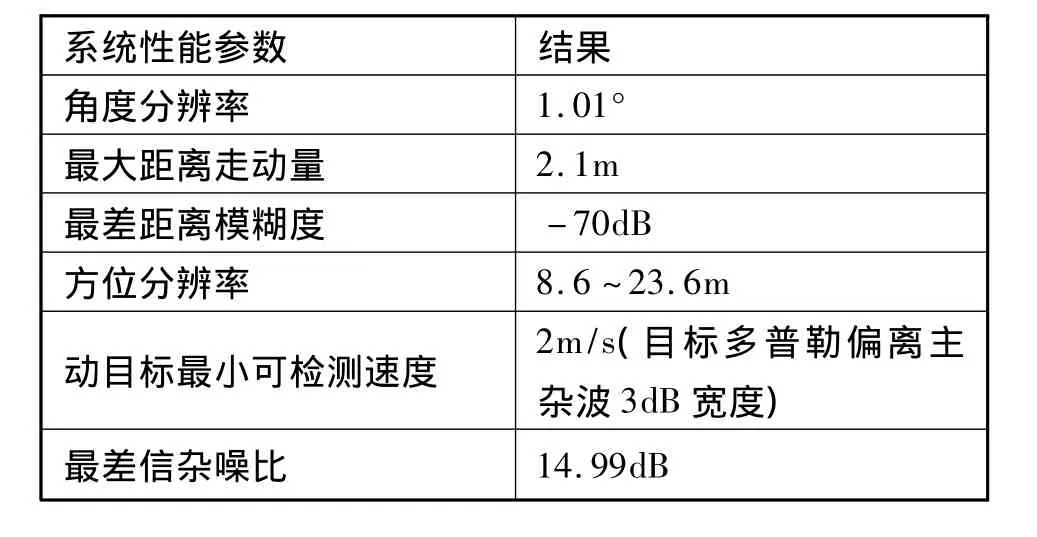
表2 静目标跟踪模式系统仿真性能参数

4 结束语［6－7］

采用DBS技术的毫米波雷达导引头可以大大提高导引头方位向分辨率，为实现目标的精确打击提供便利。本文介绍了DBS的基本概念和工作原理，并且从工程实现出发，给出了一种具有实际意义的DBS成像算法。仿真结果表明，该方案是可行的。由此可以证明DBS毫米波雷达导引头可以实现较高精度角分辨率和方位向分辨率，同时可以区分动目标和静目标，保证了后续检测、跟踪和测角的顺利进行。

［1］ 宋万忠.无人机载毫米波合成孔径雷达技术［J］.电讯技术，2002，42(6):4-7.

［2］Tobin M.Real Time Simultaneous SAR/GMTI in a Tactical Airborne Environment［C］.European Conference on Synthetic Aperture Radar.1996，63-66.

［3］周荫清.机载脉冲多普勒雷达 DBS技术［J］.航空学报，1988，9(12):574-581.

［4］Hu G，Ye X，Hu X，et al.A novel method for squint SAR image reconstrustion and graphic Correction based on the SPECAN algorithm［C］.Industrial Electronics and Applications(ICIEA)，2013 8th IEEE Conference on.IEEE，2013:640-645.

［5］ Pand L，Wang I，Zhu B.EPGA based SPECAN algorithm implementaion for ScanSAR imaging［C］.Radar Conference(EuRAD)，2012，9th，European:IEEE，2012:38-41.

［6］宋大伟.机械扫描雷达 DBS成像技术研究［D］.西安:西安电子科技大学硕士论文，2007.

［7］ 张直中.多普勒波束锐化(DBS)理论和实践中若干问题的探讨［J］.现代雷达，1991，13(2):1-12.